基于Simulink的控制系统优化设计
2022-10-27成都理工大学工程技术学院李欣莲李自成廖兴泰
◇成都理工大学工程技术学院 李欣莲 李自成 周 彬 张 媛 廖兴泰 童 强
为了简化控制系统的设计步骤并提高优化设计效率,运用Matlab软件中Simulink库的仿真功能建立需要分析的控制系统模型,选用直观简单操作的SRO软件包整定模型中的系统参数,并运用最优计算获得最优目标函数,SRO会自动地通过时域约束转变为最优化约束问题来对信号约束的问题转化,并进行最优计算矫正整定参数完成控制系统的优化设计。SOR软件包的运用使得对控制系统的设计优化成为一种操作简单,方法实用及高效的过程。
在控制系统设计中,优化设计是很关键的一点,控制系统设计的目的主要是对控制器的设计,通过矫正装置的参数整定,使系统性能在所给的函数下达到最优[1]。优化设计主要对参数进行寻优,在以往的分析中最常用的是相平面法和描述函数法,这是一项非常复杂且繁琐的过程,本文采用SRO软件可以简单高效的完成此项任务。
1 控制系统优化设计概述
对控制器进行的参数整定就是对控制系统的设计。控制系统优化设计是确定所给目标函数下可以达到最优的参数,并且是在被控对象已经确定,控制器的结构和形式也都全都已知的情况下进行。图1所示的就是优化设计过程框图。
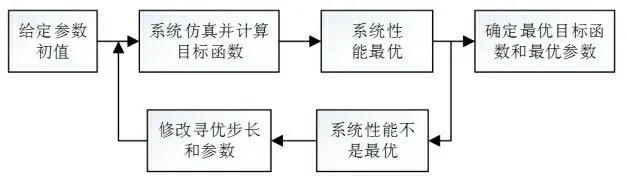
图1 控制系统优化设计过程框图
2 SRO软件包简介
Simulink响应最优化(Simulink Response Opimization,SRO)软件包[2]是Simalink6.0以上版本所提供的一个实用工具包,用来进行控制系统的优化设计。这个软件包也是NCD软件包(非线性控制设计)的升级版本。
SRO能够通过整定模型中的系统参数来达到时域性能要求,并且模型中所存在的变量也可以通过SRO来整定。SRO简洁、直观的界面使得到最优的目标函数和整定参数的过程更加简洁明了。解决最优化约束问题,就要把这个问题公式化处理,运用Matlab中的Simulink进行系统的仿真,再去对比仿真出来的结果与目标函数之间的差距后,通过最优计算去矫正整定参数。
SRO的功能与运用也就是通过给定的性能指标进行优化设计,性能指标成为约束边界,并约束系统的阶跃响应,最优化指定的整定参数。
3 给定性能指标的优化设计
以非线性控制系统设计为例,使用SRO软件包进行系统最优化设计。控制系统结构图如图2所示。
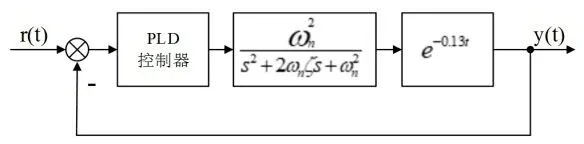
图2 控制系统结构图
其单位阶跃响应性能指标如表1所示。

表1 单位阶跃响应性能指标
PID控制器参数的初始值为:Kp=1.76291,Ti=0.935268,Td=0.321647。被控对象模型参数wn=2rad/s,ζ≈0.9。确定满足上述性能指标的PID控制器参数Kp、Ti和 Td。
(1)首先建立模型[3],将输出y(t)连接signal constraint模块,如图3所示,并命名为exmsro.m。
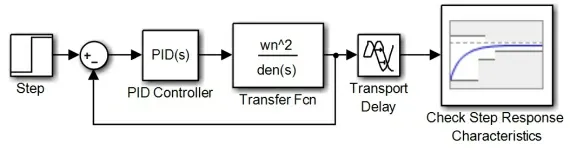
图3 exmsro.m模型
其中主要模块参数设置:①r(t)模块:Step time设置为0,Final time设置为1;②Transfer Fen模块:Numerator cofficient栏填写[wn^2];Denominator coeffici栏填写[12*wn*zeta wn*2]。
(2)打开SRO软件包的信号约束窗口。打开exmsro.m中的Signal Constraint模块,信号约束窗口的显示如图4所示。
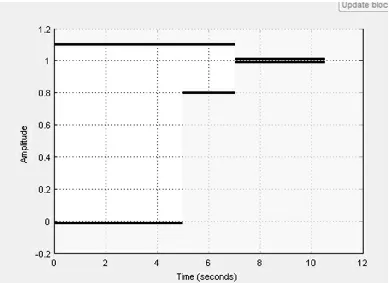
图4 信号约束窗口
约束条件:Rise time为1s,Settling time为3s,Over shoot为10%。进行参数最优化时,选Enforce signal bounds项,则相应的约束信号就会位于约束边界段内。
(3)设置期望响应约束。选择Signal Constraint模块窗口菜单Goals| Desired Respose,打开期望响应设置窗口[4]。再选中Specify step response characteristics按钮,则的阶跃响应性能指标设置界面,参数设置如表2所示。
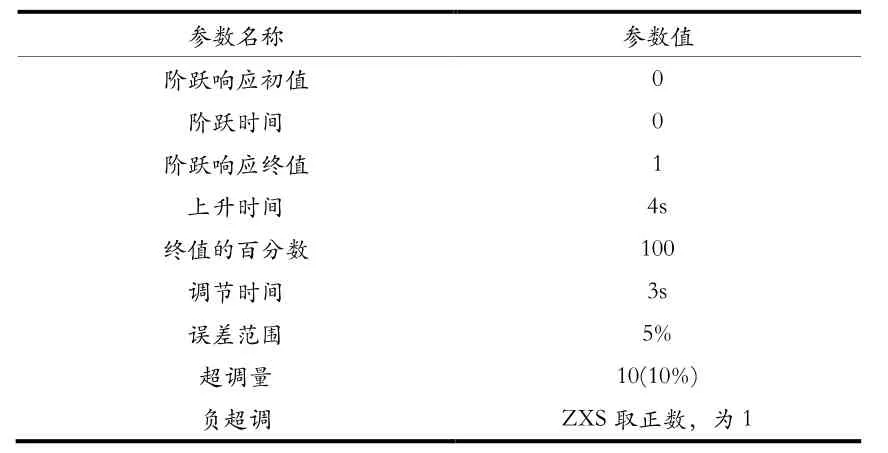
表2 阶跃响应性能指标参数
此时阶跃响应约束形状如图5所示。
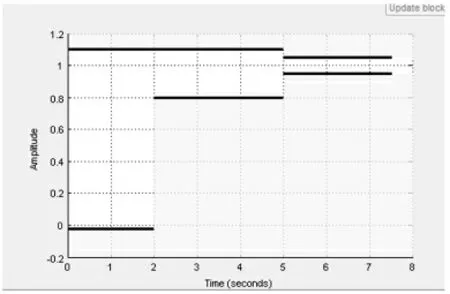
图5 设置后的信号约束窗口
(4)定义变量,在模型中去定义未知的变量,本例需定义的5个变量:Kp、Ti、Td、wn及ζ。
在Matlab命令窗口中输入:>>Kp=1.76291;Ti=0. 935268;Td=0. 321647;wn=2;zeta=0.9;随后该5个变量被定义。
(5)指定整定参数[5]。进行参数最优化前需要指定PID控制器参数(Kp, Ti和 Td)。首先在约束窗口中打开整定参数对话然后点击Add按钮,打开添加参数窗口,在此参数窗口选中Kp、Td和 Ti,确定后就可以把它们添加到整定参数对话窗口中。
(6)最优计算。完成以上操作后,开始可以使用参数的最优计算(选择信号约束窗口中的Optimization |Start)。SOR会通过工具箱中的函数来进行最优计算并调节整定参数[6]。
在Matlab的命令窗口中输入:>>Kp,Ti,Td;运行结果为:Kp=1.8241;Ti=1.2106;Td=0.8130。
由此得到满足上述性能指标的PID控制器参数Kp、Ti和 Td。
(7)保存项目。SRO会在创建一个最优化项目后再进行最优计算,此项目包含有阶跃响应约束(来自模型中的所有信号约束窗口),以及整定参数的设置,参考信号设置,不确定参数设置,最优化设置和仿真设置。
4 结论
为了使Simulink模型中的系统参数达到用时域窗口对信号对图形约束或者跟踪参考信号获得的性能要求,使用SOR软件包是快捷高效的方法。SRO还能够整定模型中存在的变量(标量、向量及矩阵等)。使用SRO须在已有的Simulink模型中添加一个信号约束(Signal Constraint)这个特殊的模块。在把模型中需进行约束的信号与此信号约束模块连接,在SRO中就会自动地把时域约束转变为最优化约束问题,最后就使用优化工具箱或遗传算法与直接搜索工具箱中的函数进行最优化算法求解。所以在Matlab用SRO软件包对Simulink建立的控制系统响应最优化是一种操作简单,方法实用及高效设计的过程。
