NO 紫外宽带吸收光谱的非线性响应及实验*
2022-10-27熊枫彭志敏丁艳军杜艳君
熊枫 彭志敏 丁艳军 杜艳君
1) (华北电力大学控制与计算机工程学院,北京 102206)
2) (清华大学能源与动力工程系,电力系统与发电设备控制与仿真国家重点实验室,北京 100084)
紫外宽带吸收光谱(UV-BAS)作为一种气体定量检测技术,常用于检测NO 等气态污染物,然而光谱仪对真实光谱的展宽作用会导致吸收率随光学厚度的变化偏离线性关系.本文针对NO 吸收光谱的非线性效应进行了理论与实验研究,通过建立NO 吸收率峰值非线性数据库,提供了一种基于插值多项式的NO 浓度测量方法.首先理论推导出吸收率随光学厚度的非线性变化关系.通过对单谱线进行仿真分析,探究仪器展宽给非线性变化关系带来的影响;然后定量计算不同仪器展宽下γ (0,0)谱带吸收率峰值随光学厚度的变化关系,并给出多项式模型的非线性表达式并建立系数数据库,同时对同一展宽不同NO 振动谱带的非线性问题进行了比较与分析.最后,通过采用不同展宽光谱仪实验测量NO 吸收光谱并对上述理论研究结果进行验证,吸收率峰值实验结果与理论计算的相对误差小于4%,与数据库插值多项式的误差小于8%,证明了理论计算的准确性与数据库的可靠性.
1 引言
氮氧化物 (NOx) 作为重要的大气污染物,对环境和人体都有着极大危害.NOx会参与平流层中自由基反应而破坏臭氧层[1,2],形成酸雨污染水体[3];在紫外线照射下易分解并与空气中化合物反应产生光化学烟雾[4];此外,NOx会对呼吸系统造成损伤[5].随着“碳减排”的发展,传统烃类燃料的替代品受到了广泛关注,NH3成为研究热点,而NH3的燃烧同样会产生NOx.95%以上的NOx来自于燃烧过程,如冶金、火力发电等.注意到,工业排放的NOx中NO 含量超过90%,所以实现NO 的精确测量意义非凡.
光谱测量技术因其非接触,响应快等优势,逐渐成为监测气态污染物的重要手段,如化学发光法[6-9]、可调谐激光吸收光谱技术 (TDLAS)[10-13]、激光诱导荧光技术 (LIF)[14-17]和宽带吸收光谱技术(BAS)[18-25].化学发光法能够通过相对简单的系统测量低浓度物质,但其需要繁琐的标定实验来得到绝对浓度;LIF 技术拥有高空间分辨率与低检测下限,但其实验系统昂贵复杂且同样需要标定来获取绝对浓度,常用于实验室测量,难以应用于环境恶劣的工业现场.与上述两种方法相比吸收光谱技术系统简单且可测量温度、绝对浓度.其中,TDLAS技术已广泛地应用于气态污染物测量,但由于红外波段吸收较弱且易受其他分子谱线干扰,对于低浓度且吸收较弱的污染物,如NO,TDLAS 技术难以实现浓度的精确测量.
与TDLAS 相比,紫外宽带吸收光谱技术 (UVBAS) 所利用的紫外波段吸收远强于红外波段;此外,燃烧主要产物 (如CO2,CO,H2O) 的紫外光谱所处位置较为分立,对NO 紫外吸收光谱的测量不存在干扰,可以更好地实现NO 浓度测量;因此诸多学者利用UV-BAS 技术实现NO 的精确测量.Peng等[18]基于深紫外差分吸收光谱建立了NO 与SO2同步测量系统,体积分数检测下限达7 × 10—9,6 × 10—8.Zhang等[22]利用UV-BAS 技术对电厂烟气中NO 与SO2进行同步检测,浓度变化范围分别为100—220,750—1300 mg/m3.Li等[23]使用差分吸收光谱对空气开关中NO 与O3进行同步测量,体积分数检测下限分别为6.40 × 10—7和3.76 × 10—6.Sepman等[24]利用低分辨率光谱仪(约1.1 nm),测量吸收分数 (1 —τ,τ为测量透过率)积分面积实现等离子体中NO 温度与浓度同步测量,浓度相对误差小于 15%,温度误差小于±40 K.
由于NO 紫外吸收光谱的结构特点,测量结果受仪器函数影响巨大,非线性问题十分严重.1969 年,Buijs等[26]认为仪器因素造成的非线性与光学厚度XL(浓度X与光程L乘积) 成多项式关系,但是该工作仅针对溶液而并未针对气体进行实验研究.Donovan等[27]利用UV-BAS 研究氧原子反应时,使用分数项 (XL)a修正(系数a=0.5—1.0),但并未对非线性问题进行分析.1996 年,Mellqvist等[28]研究表明气体的非线性问题是由仪器对真实光谱的展宽作用导致.使用方波仪器函数对非线性行为进行理论推导,发现仪器展宽内真实吸收截面结构变化越明显,非线性问题越严重.Trad等[29]计算不同温度下NOγ(0,0)与γ(1,0)的谱带跃迁,通过激波管实验进行验证;并使用光学厚度的平方项 (XL)2对测量吸收率结果进行修正.但激波管有效实验时间较短,实验结果相对误差较大.
本文针对NO 的非线性问题进行了理论实验研究,理论推导了NO 吸收率峰值随XL的变化关系.首先,通过对单谱线进行仿真分析,探究仪器展宽给非线性变化关系带来的影响.接着,定量计算不同仪器展宽下NOγ(0,0)谱带吸收率峰值随XL的变化关系,给出多项式形式的非线性表达式并建立系数数据库.最后,对NO 不同谱带间的非线性变化关系进行了分析与比较.此外,理论推导发现积分面积随XL的变化关系与仪器函数无关,计算并比较不同谱带吸收分数积分面积的变化行为.通过两台不同仪器展宽的光谱仪对NO 吸收光谱进行实验测量进而对上述理论探究结果进行验证,实验结果与理论计算、数据库插值结果均符合较好,证明了理论计算的准确性与数据库的可靠性,为NO 定量测量提供新思路.
2 非线性理论模型
2.1 宽带吸收基本原理
根据Beer-Lambert 定律,气体会吸收部分波长的入射光线,光强透过率可以表示为τ(ν)=It(ν)/I0(ν)=exp[-α(ν)].α(ν)为吸收率:
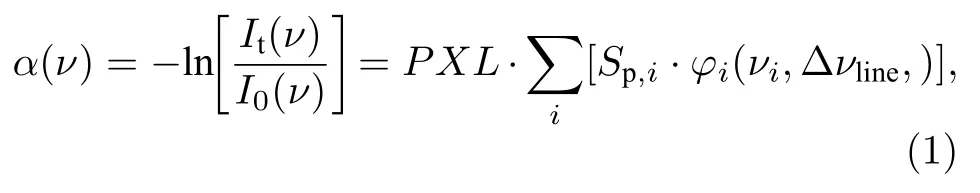
式中,ν(cm—1) 是波数;I0(ν),It(ν)分别是入射与透射光强;φi(ν) (cm)为线型函数,由谱线位置νi(cm—1)与真实展宽Δνline(cm—1)决定,包括碰撞展宽、多普勒效应等;p(atm,1 atm=101325 Pa)是绝对压力;X为体积浓度;L(cm)为光程;Sp,i(cm—2·atm—1)为单位压力线强度,下标i表示每一特定跃迁.Sp,i表达式为

式中h(J·s)为普朗克常数,c(cm/s)为光速,k(J/K)为玻尔兹曼常数,T(K)为绝对温度,gn为简并度,Q(T)为配分函数,νi(cm—1),Bi(cm3·J—1·s—2),J′和E″(J)为对应跃迁的中心波数,爱因斯坦受激吸收系数,上能级转动量子数与下能级值.gn,Q(T),νi,Bi和E''可以从Lifbase 或EXOmol 等数据库中查找[30,31].
BAS 利用较大波长范围内的光谱信息进行测量.为方便应用,吸收率α(ν)常表示为吸收截面σ(ν)与光学厚度XL(即浓度X与光程L乘积)的乘积:α(ν)=σ(ν)·XL.温度、压力确定,物质吸收截面σ(ν)为定值,真实吸收率α(ν)随光学厚度XL线性变化.然而由于光谱仪等光学设备不能完美分辨不同波长的光强信号,某一波长的信号会影响其他波长处信号的强度,导致真实光谱被模糊化.这种现象可用仪器函数φin(ν) 来描述,一般为Gauss 线型,其半高全宽 (FWHM)为光谱分辨率,又称为仪器展宽Δνin.测量光强信号与真实光强信号并不相同,可以表示为仪器函数φin(ν)与真实光强的卷积:=φin⊗It,=φin⊗I0.若原始光强I0随波长缓慢变化,则有φin⊗I0≈I0.此时,测量透过率τd表示为由于仪器函数φin(ν)作用,测量光强信号的强度与结构发生了明显的变化,测量吸收率αd(ν)=-ln偏离真实吸收率α(ν),不随光学厚度XL线性变化.BAS 可以通过峰值与积分面积来获取气体参数,后文将分别对二者随XL的变化行为进行理论推导.

2.2 峰值随光学厚度的变化
BAS 测量吸收率αd(ν)计算表达式为

式中,φin(ν)为仪器函数,α(ν)是无仪器函数作用时的真实吸收率.由于φin(ν)作用,实际测量得到的吸收率αd(ν)并不随XL线性变化,对(3)式指数函数进行泰勒展开得:
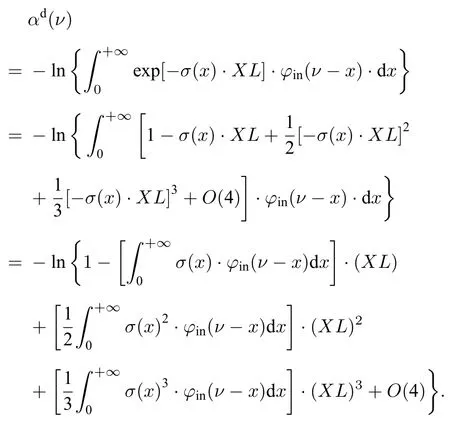
当测量系统与待测气体均确定时,σ(ν)与φin(ν)固定,积分为定值,(3)式可化为
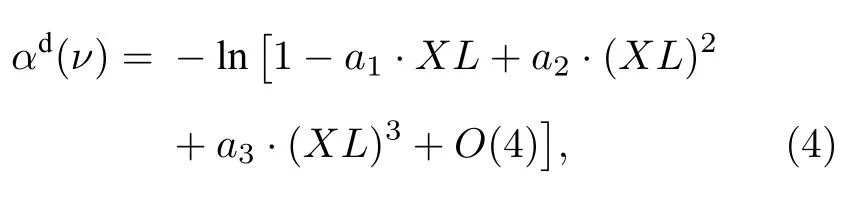
其中,
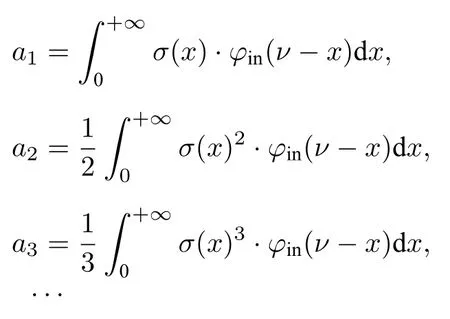
再次进行泰勒展开可得:
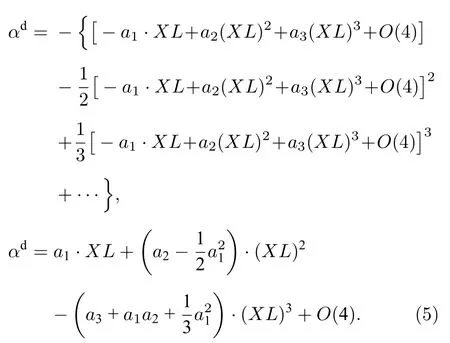
可以看出,αd(ν)随XL的变化并不是简单的线性关系,还包含XL的高次项成分,且高次项影响程度与σ(ν)和φin(ν)均有关.由于多项式形式简洁、使用方便,用三次多项式来描述测量吸收率峰值随XL的非线性变化关系,并在后文建立不同Δνin下变化的多项式系数数据库.实际应用中,一旦确定Δνin便可利用数据库中系数插值得到随XL的多项式关系:

其中,A1—A3为各项式系数.由此可避免繁琐的标定过程,为实际测量提供参考数据.
2.3 积分面积随光学厚度的变化
定义吸收分数A=1-τ,则测量吸收分数Ad与真实值A有如下关系:

其中τ与τd分别为测量透过率与真实透过率.对测量吸收分数Ad进行积分并交换积分次序可得:
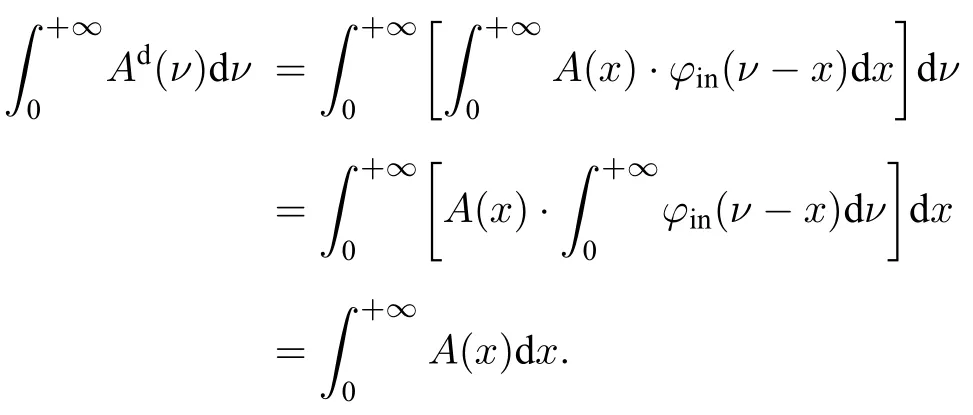
可以看出,Ad与A的积分面积相同且与φin(ν)无关.再对指数函数进行泰勒展开可得:
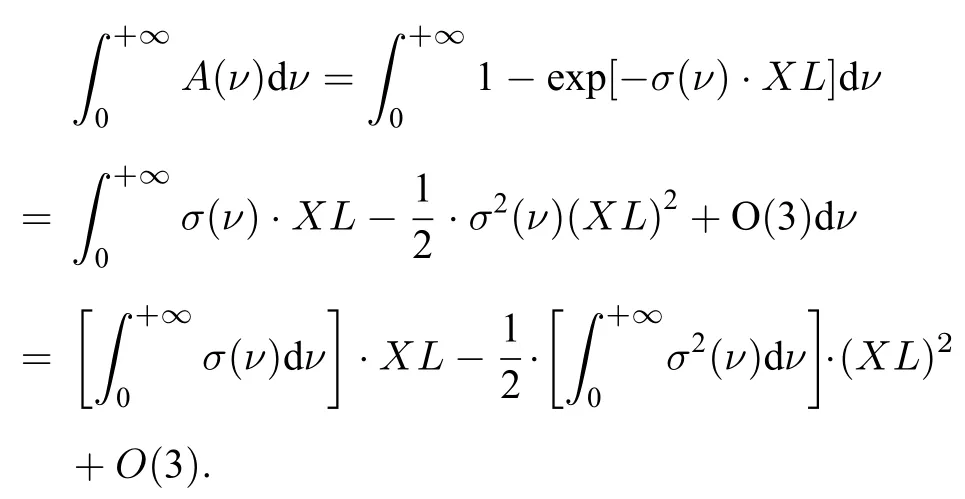
经推导计算,最后得出如下关系:

Ad的积分面积随XL的变化同样具有多项式关系,并且各次系数仅与σ(ν)有关而不受φin(ν)影响.
3 实验系统
UV-BAS 测量NO 吸收光谱的实验装置主要分为两大部分: 光谱测量系统和气体配置系统,如图1 所示.在光谱测量系统中,氘灯作为光源可产生200—600 nm 波长范围的连续紫外-可见光.氘灯出射光线经过凸透镜1 初步准直后进入直径5 cm,长50 cm 的石英气室.气室出射光线经过凸透镜2 汇聚到光纤接口处,通过光纤传输进入光谱仪.为探究仪器展宽对NO 吸收光谱非线性效应的影响,实验使用两种不同型号光谱仪测量光强信号,采集不同仪器展宽下NO 的吸收光谱.光谱仪1为爱万提斯Starline 系列多通道便携式光谱仪.光谱仪2为Andorra SR-303I,配置1200 g/mm 光栅.配合使用ICCD 相机 (Andorra Istar 334T) 用于记录光强信号.

图1 UV-BAS 测量系统示意图Fig.1.Schematic of the experimental setup for UV-BAS measurements.
气体配置系统中,使用体积分数为2.001 × 10—3NO 标准气体作为待测气体,99.999%的高纯N2作为稀释气体.NO 与N2的质量流量通过质量流量计进行控制,以得到不同浓度的NO 待测气体.两路气体进入不锈钢混合气室充分混合后通入石英气室进行测量.气室压力由压力传感器测量得到,通过两阀门来调节气室压力在1 atm 左右.待测气体充满气室后静置约30 s,压力传感器示数保持不变后开始测量NO 吸收光谱.气体温度近似认为室温,由水银温度计测量得到.
4 结果与讨论
4.1 仿真分析
4.1.1 单谱线非线性问题
针对单根谱线进行研究,分析仪器展宽Δνin对单谱线吸收率峰值非线性行为的影响.将仪器展宽Δνin与谱线真实展宽Δνline的比值定义为相对宽度Δ=Δνin/Δνline.图2 展示了不同相对宽度Δ下,随光学厚度XL的非线性行为,虚线为无仪器函数作用时的真实吸收率α.非线性程度随Δ增大而加深,但随着Δ值增大,曲线相互靠近,这意味非线性度的变化程度与Δ的大小有关.
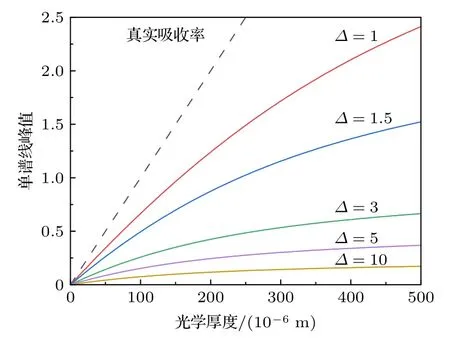
图2 单谱线峰值随光学厚度变化的非线性行为Fig.2.Nonlinearity of single line peak with optical thickness.
为对非线性行为进行定量描述,用三次多项式对非线性曲线进行拟合,得到各次系数A1,A2,A3,并定义二次项与一次项系数比值的绝对值为非线性度ζ=|A2/A1|.非线性度ζ随相对宽度Δ的变化及其导数如图3 所示,黑色圆点代表非线性度,红色实线代表导数.其中ζ导数随Δ先增大后减小,当Δ=0.849 时,ζ导数达到最大值.当Δ< 0.172,非线性度ζ< 2 × 10—6,小于ζ最大值(Δ=10)的千分之一,这表明当Δνin< 0.172Δνline时,非线性问题可以忽略.从单根谱线的非线性行为可以明显看出: 当仪器展宽Δνin与谱线自身展宽Δνline相近时,Δνin变化会造成非线性行为的剧烈变化;而当Δνin远小于(实际仪器几乎不可能达到)或远大于Δνline时,非线性行为对Δνin的改变并不敏感,即非线性行为变化的剧烈程度与相对宽度Δ的大小有关.该结果与文献[28]的研究结果基本一致,两者的差异是由于得到系数A1,A2的方式不同,本文使用三次多项式对非线性曲线进行最小二乘拟合,而文献[28]则给出系数A1,A2的表达式并计算非线性度ζ.
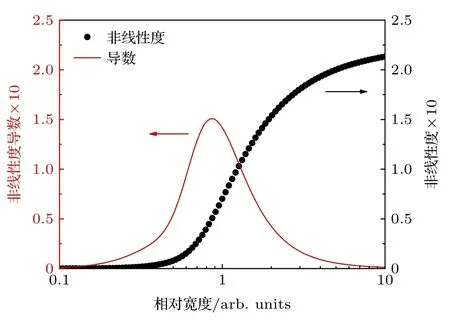
图3 单根谱线非线性度及其导数Fig.3.Nonlinearity of single line and its derivative.
4.1.2 NOγ(0,0)谱带吸收率峰值的非线性变化行为
气体在紫外波段的吸收是由于分子不同电子能级的各级振转能级间跃迁产生的,NO 最为常见的电子带系跃迁为电子能级基态X2Π 到第一激发态A2Σ+的跃迁,A2Σ←X2Π,又称为γ带系跃迁;此外,不同振动能级间跃迁的谱分布位置同样不同,A2Σ,ν′=0←X2Π,ν′′=0,记为γ(0,0),表示从基态电子态ν′′=0 振动带跃迁到第一电子激发态ν′=0 振动带;而γ(1,0)表示A2Σ,ν′=1←X2Π,ν′′=0 谱带跃迁.
NO的γ(0,0)振动谱带所处波长最长且吸收较强,常用于实际测量,对该谱带的非线性行为进行研究.当X=1 × 10—4,T=290 K,p=1 atm,L=100 cm 时,NOγ(0,0)谱带的真实吸收率α(ν)与不同仪器展宽Δνin下的测量吸收率αd(ν),如图4(a),(b)所示.NO 单个振动谱带包含数千条独立跃迁,α(ν)光谱结构变化明显,而测量光谱为真实光谱中各点在测量范围内按φin(ν)加权求和后的结果,导致αd(ν)光谱结构发生极大改变.从图4 可以看出,相比于α(ν)光谱结构,φin(ν)明显平滑,使测量吸收率峰值减小,且随着Δνin值增大,αd(ν)的光谱结构趋向于单一、光滑且峰值更小.
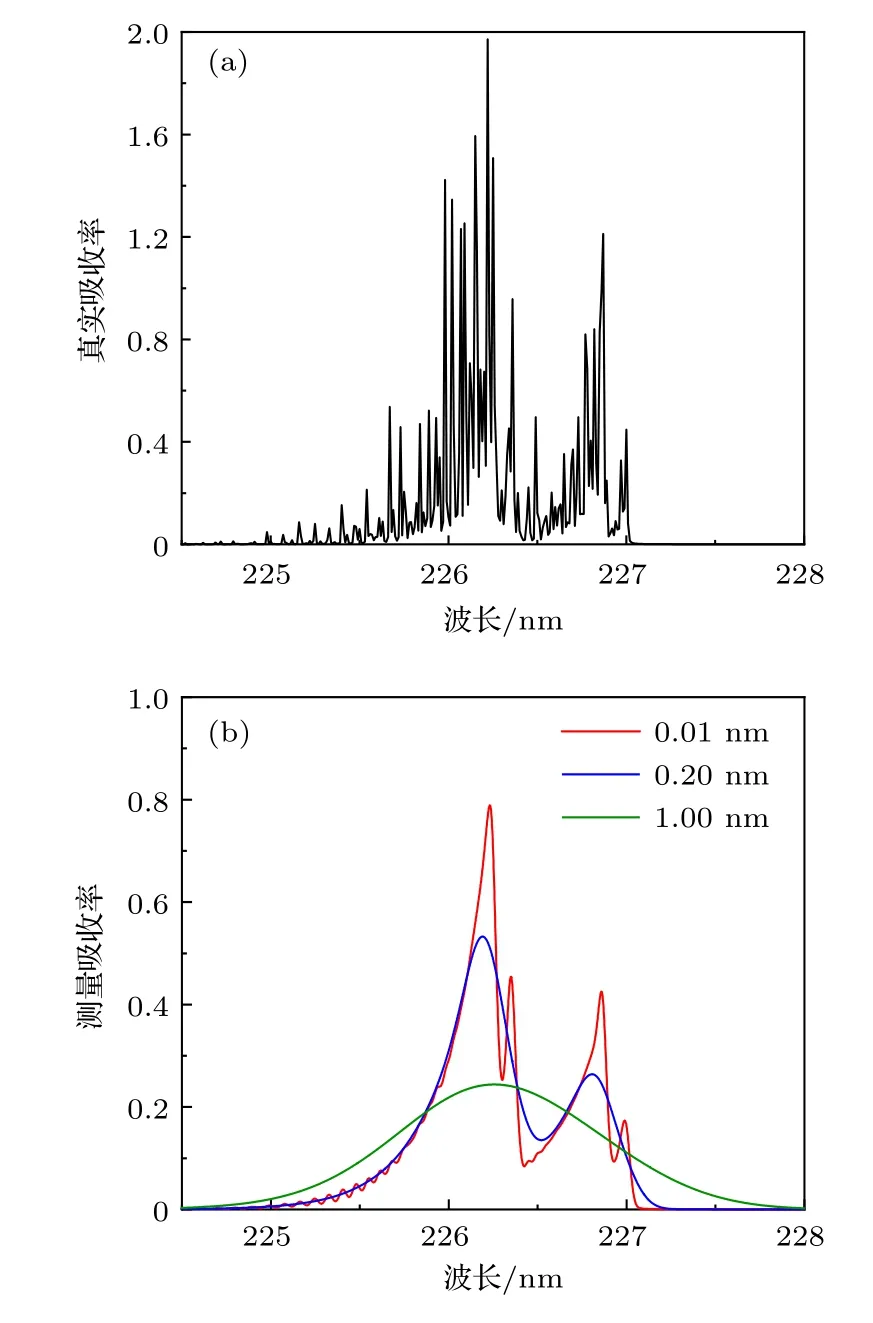
图4 γ (0,0)带系吸收光谱 (a) 真实光谱;(b) 不同仪器展宽下的测量光谱Fig.4.Absorption spectra of γ (0,0): (a) True spectrum;(b) detect spectra in different instrument widths.
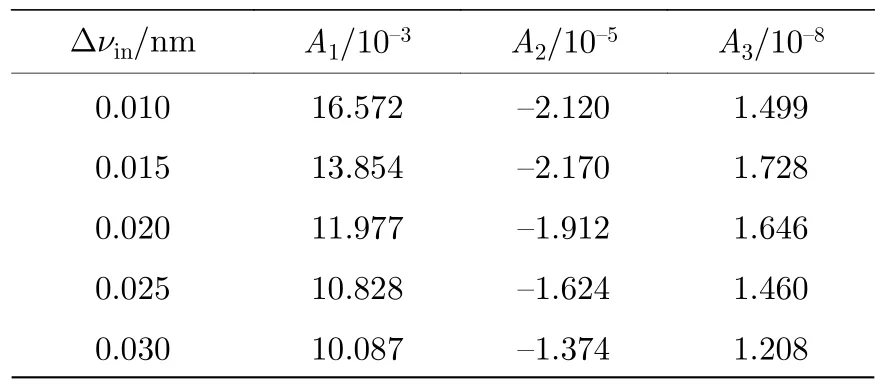
图5 展示了不同仪器展宽Δνin下γ(0,0)谱带的非线性行为,虚线为无仪器函数φin(ν)作用时,真实吸收率α(ν)的变化曲线.可以看出α(ν)随XL线性变化并且其峰值αpeak远大于测量吸收率峰值.使用三次多项式对的非线性曲线进行拟合,得到各次系数A1,A2,A3与非线性度ζ.由于光谱仪很少具有极高或极低的分辨率,故取仪器展宽范围为0.01 nm< Δνin< 5.00 nm.表1展示了部分展宽下的A1,A2,A3的拟合结果,详细非线性系数数据库见附录表A1.在实际过程中,当Δνin值确定,可以通过数据库插值即可得到相应随XL的变化曲线,避免复杂的标定过程.

表1 NO 非线性行为的多项式系数Table 1.Polynomial coefficient for NO nonlinearity.
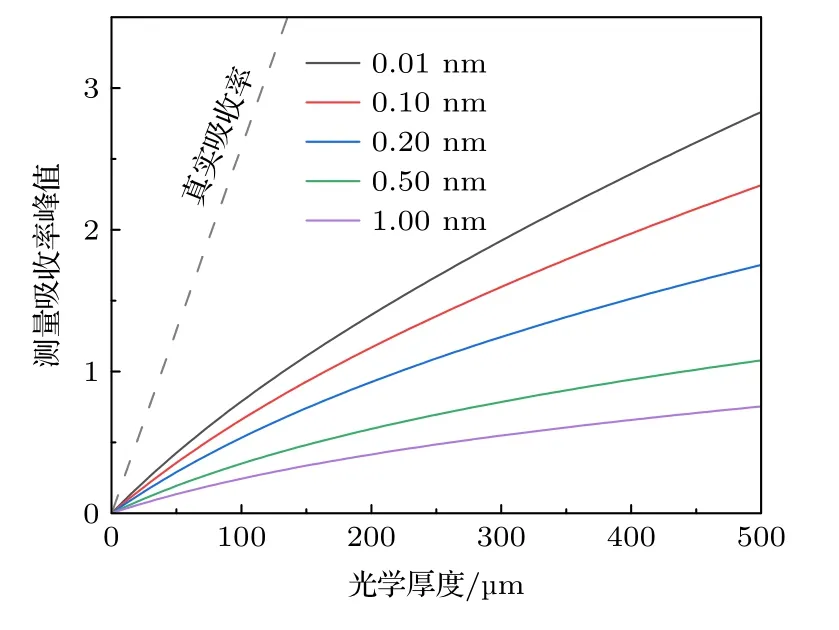
图5 不同仪器展宽下γ (0,0)带系吸收率峰值非线性行为Fig.5.Nonlinearity of the peak absorbance in γ (0,0) in different instrument widths.
单根谱线非线性度ζ随相对宽度Δ的变化具有明显的规律性.但实际光谱包含众多跃迁,在谱线真实展宽的作用下,不同跃迁轮廓相互叠加耦合,使NO 真实吸收光谱的非线性行为与单根谱线差异极大.图6 展示了NO 非线性曲线一、二次项系数A1,A2与非线性度ζ随仪器展宽Δνin的变化规律.随着Δνin值增大,测量光谱与真实光谱间的差异增大,结构改变更加明显,αd(ν)偏离线性的程度越深,一次项所占得比重越来越低,故一次项系数A1随着Δνin单调递减.而二次项系数|A2|随着Δνin先增大后减小.当Δνin值较小时,一次项占据主导,非线性效应主要由二次项导致,|A2|随Δνin增大,使αd(ν)非线性程度加深;但随Δνin值进一步增加,更高次项对非线性行为的影响愈发明显,同时一次项在αd(ν)中所占比例已经较低,导致|A2|随Δνin开始减小.

图6 A1,|A2|与非线性度随仪器展宽的变化规律Fig.6.Dependence of A1,|A2|,and the relative nonlinearity on the instrumental width.
非线性度ζ的变化过程可以大致分为三个区域.区域I: Δνin< 0.018 nm.此时,一次项系数A1随Δνin值的增大而单调下降,二次项系数|A2|同样增大,但增长速率先快后慢.该区域中仪器展宽Δνin与谱线自身展宽Δνline相近,非线性度ζ对Δνin数值变化十分敏感,ζ快速增大到局部最大值1.61 × 10—3.区域II: 0.018 nm< Δνin<0.066 nm.A1值较小,一次项在αd(ν)中所占比例较小,限制了二次项系数|A2|的增长.该区域中A1与|A2|同时下降,由于|A2|下降速度更快,导致非线性度ζ下降到局部极小值1.17 × 10—3.区域III: Δνin> 0.066 nm.此 时Δνin≫Δνline,A1与|A2|均随Δνin增大而缓慢下降,|A2|下降更加缓慢,使得非线性度ζ缓慢上升;在区域IV 范围内,由于A1已足够小,|A2|变化速度的微小变化导致ζ出现波动,但由于变化并不剧烈,ζ在区域III 中仍可认为是单调增加.
4.1.3 NO 不同振动谱带非线性问题对比
对NO 不同振动谱带的非线性行为进行研究,在X=1 × 10—4,T=290 K,p=1 atm,L=100 cm,Δνin=0.1 nm 的条件下,理论计算了NOγ带系的测量吸收率αd(ν)光谱,结果如图7 所示.αd(ν)不同谱带光谱结构相似;但γ(1,0)谱带的吸收率远强于γ(5,0)谱带,无法直接比较不同谱带的非线性行为.
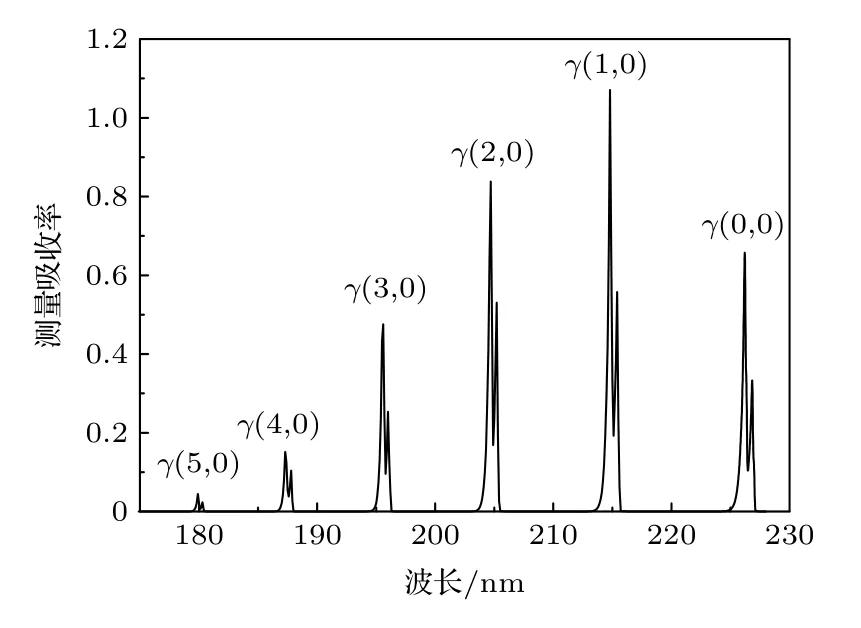
图7 NO 不同振动谱带紫外吸收光谱Fig.7.NO absorbption spectra in different vibration bands.
不同振动谱带测量吸收率峰值随XL的变化如图8(a)所示.随着XL增加,单调递增,但增长速度逐渐变慢.不同谱带间吸收强度差异较大,图8(a)中各曲线高低不一,无法直接进行比较分析.将不同谱带线强度S0分别乘以常数,使线强度最大值Smax相同.淡化吸收强度的影响之后,各带系的非线性行为如图8(b)所示.不同谱带间非线性行为存在差异,由2.2 节理论推导可知,峰值非线性行为与真实吸收截面σ(ν),仪器函数φin(ν)有关.不同谱带的谱线分布存在差异,真实吸收截面σ(ν)不同,导致不同谱带间非线性行为的不同.图8(b)中最上方为γ(0,0)的非线性曲线,表明其偏离线性的程度最轻;γ(4,0)的曲线位于最下方,非线性问题最严重.γ(1,0),γ(3,0)与γ(2,0),γ(5,0)交织紧密,非线性程度相近,这是由于谱线分布较为相似,真实吸收截面σ(ν)差异较小.注意到弱吸收(< 0.5)时,不同谱带非线性曲线彼此接近.由理论推导可知,αd(ν)与XL具有多项式关系,在XL值较小时,高次项数值较小,αd(ν)主要由XL一次项的决定并且接近真实吸收率α(ν),非线性问题并不明显;而各带系Smax相同,真实吸收率峰值αpeak接近,因此弱吸收时不同谱带峰值非线性行为差异较小.
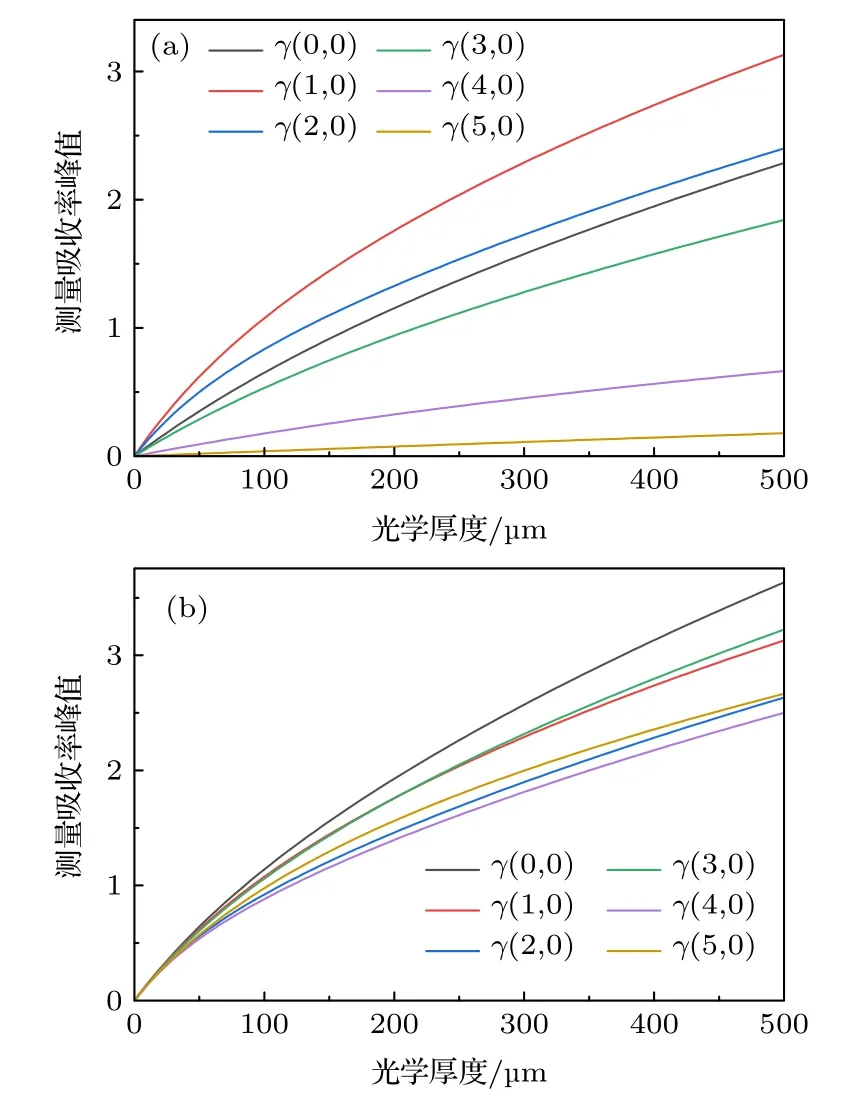
图8 (a) 不同谱带吸收率峰值非线性行为;(b) 等最大线强度各谱带峰值非线性行为Fig.8.(a) Nonlinearity of peak absorbance in different bands;(b) nonlinearity of peak absorbance with the same maximum line strength in different bands.
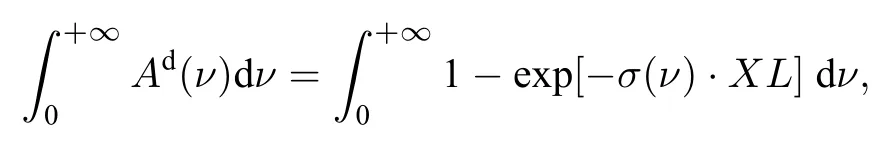
其变化曲线弯曲更加明显.同样使不同谱带线强度最大值Smax相同来消除吸收强度差异后,积分面积随XL的非线性变化行为如图9(b)所示.对比图8(b)与图9(b)可以定性看出,在淡化吸收强度影响后,相对于吸收率峰值,不同谱带间积分面积的非线性行为的差异更小,这是由于Ad与A的积分面积相等,等于所有独立跃迁谱线轮廓的面积之和,不同谱带间虽然谱线相对分布不同,但跃迁谱线条数相差较小,故Smax相同时,积分面积相差较小.这表明不同谱带间光谱结构的差异主要是由于谱线相对位置不同,而总跃迁数目相差较小.谱线位置分布主要影响真实吸收截面σ(ν)结构,对影响较大,而对积分面积影响较小.在弱吸收工况下,不同谱带间积分面积的非线性行为同样较为接近,仅在吸收较强时才会表现出明显不同,这与峰值的非线性行为相似.
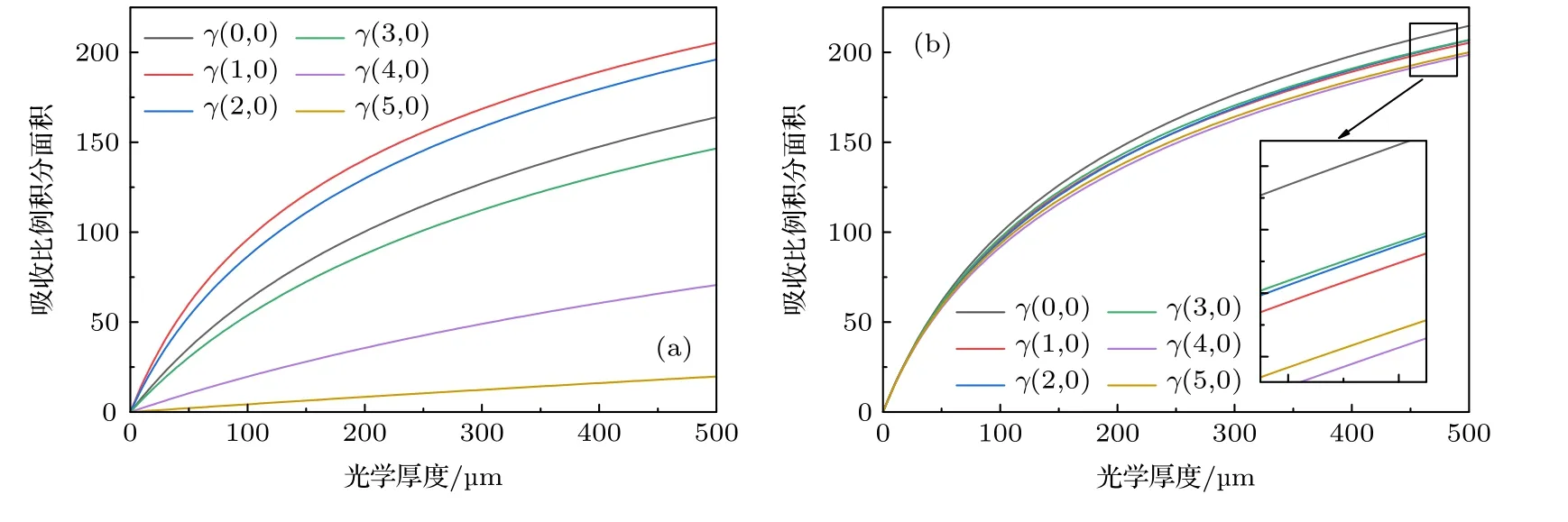
图9 (a) 不同谱带吸收比例积分面积非线性行为;(b) 等最大线强度各谱带面积非线性行为Fig.9.(a) Nonlinearity of absorption fraction the integral area in different bands;(b) nonlinearity of the integral area with the same maximum line strength in different bands.
4.2 实验研究
使用两台光谱仪测量不同仪器展宽Δνin下NO 的吸收光谱.根据Beer-Lambert 定律,需要测量无吸收时的原始光强I0,存在吸收时的透射光强It与背景光强Ib.图10 展示了上述三类光强信号,测量吸收率与拟合结果.图10(a)为光谱仪1测量的光谱信号,单次曝光时间0.7 s,进行100 次平均来提高信噪比;图10(b)为光谱仪2 的测量信号,单次曝光时间150 ms,100 次平均.图10(c),(d)分别为实验结果与拟合结果的对比.可以看到吸收率拟合的误差在2%以内,证明拟合结果的准确性.实验中吸收率基线大于零,产生基线漂移的现象,使用多项式对拟合结果的基线进行调整得到更好的拟合实验结果.拟合结果在峰值处易出现结构性残差,是由于吸收最强处光强最弱,噪声给光强测量带来的干扰最大;此外Voigt 线型函数无法精确描述谱线轮廓,这些都会导致结构性残差的产生.

图10 UV-BAS 测量光谱强度与吸收率 (a),(b) BAS 光谱强度;(c),(d) BAS 测量吸收率Fig.10.Spectrum intensities and absorbances measured by BAS: (a),(b) BAS spectrum intensity;(c),(d) BAS measures absorption.
光谱仪1 的仪器函数可用Gauss 线型很好地描述,在226 nm 处展宽Δνin=0.25 nm;光谱仪2的展宽包含Lorentz 成分,使用Voigt 线型进行描述,在226 nm 处展宽Δνin=0.39 nm.光谱仪1展宽Δνin更小,αd(ν)结构起伏更加明显,但由于其为便携式光谱仪,其测量光谱信号更加粗糙,在单位波长的数据点较少,波长的分辨率较低且随机噪声更加明显.光谱仪2 的波长分辨率更高,测量信号受噪声影响较小,测量光谱质量更高,但其展宽Δνin更大.这表明Δνin与波长分辨率并不绝对相关,Δνin值更小的仪器测量得到的光谱质量不一定更好.仪器函数φin(ν)应为Gauss 函数,而实际应用中的非理想因素会使φin(ν)包含Lorentz成分,可以使用Voigt 函数进行描述.Gauss 与Lorentz 线型对实际光谱形状改变的程度也不同.相同半高全宽(FWHM),Lorentz 线型向两翼的展宽程度更大,对光谱结构改变更大,使吸收率峰值的衰减更加明显.故Δνin值越大,Lorentz 成分越高,αd(ν)的非线性问题越严重.Gauss 线型不一定适合所有测量系统,实际中选用适合的φin(ν)十分重要.
4.2.1 吸收率峰值的非线性变化关系
图11 展示了实验测量吸收率峰值的非线性行为并与理论计算结果进行对比.黑色实线为理论计算结果,彩色点表示实验结果.实验结果与理论计算的相对偏差在±5%的范围内,表明理论计算可以很好地描述非线性行为.光谱仪1 的仪器函数φin(ν)可以用Gauss 线型很好地描述.为验证系数数据库的准确性,根据仪器展宽其Δνin在附表中插值得到相应的峰值非线性多项式:αd=5.720 × 10—3x—8.073 × 10—6x2+6.105 × 10—9x3,其中x为光学厚度XL.图12 对比了插值多项式与实验结果.相对误差在8%以内,充分证明了多项式系数数据库的可靠性.需要注意的是,本文仅计算0<XL< 5 × 10—4m 范围内的非线性行为并给出多项式系数,插值多项式在该范围能很好地描述峰值非线性行为,超过该范围插值结果误差较大.通过理论计算建立的多项式系数数据库能够极大简化实际测量过程,确定测量系统的仪器展宽Δνin后就可以插值得到随XL变化的多项式关系.免去复杂的标定过程,具有重要的指导意义.
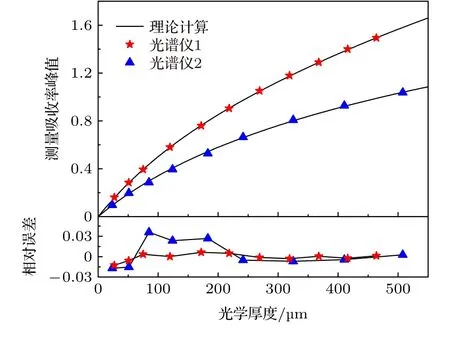
图11 吸收率峰值随光学厚度变化规律Fig.11.Dependence of the peak absorbance on optical thickness.
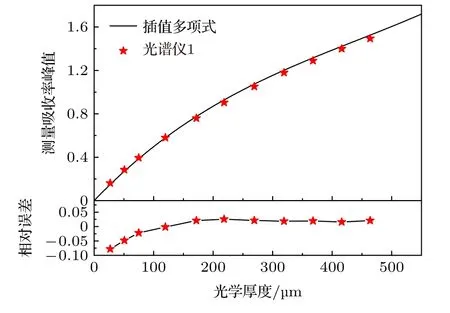
图12 数据库系数插值多项式与实验结果对比Fig.12.Comparison between interpolation polynomial and experimental result.
4.2.2 吸收分数积分面积的变化关系
吸收分数Ad积分面积的非线性行为与仪器函数φin(ν)无关,不同系统测量的Ad积分面积随XL的变化规律相同.分别对两台光谱仪的测量吸收分数Ad进行积分并与理论计算结果相比较,结果如图13 所示.可以看出不同光谱仪测量的非线性行为基本一致,这表明积分面积的变化行为不受φin(ν)影响;光谱仪1 实验结果的相对误差小于3%,光谱仪2 的相对误差小于6%,证明理论计算的准确性.注意到实验结果均小于理论计算,可能原因有: 1)仪器函数φin(ν)导致波峰沿波长向两侧无限延伸,受设备和其他谱带吸收峰的干扰,测量不能覆盖足够的波长,只能在有限范围内对Ad进行积分;2)多项式拟合无法完全消除基线漂移的影响;3)实验结果为测量数据的梯形数值积分,在两测量点间为下凹(或上凸)时,梯形面积会大于(或小于)该微元范围内的实际面积;4)随机噪声的积分面积可能不为零.光谱仪2 的Δνin值较大且包含Lorentz 成分,导致吸收峰向两翼展宽严重,有限范围的积分会导致更大的相对误差.光谱仪1 的Δνin值较小,有限范围积分影响相对较小;但由于其波长分辨率较低,需要考虑梯形数值积分产生影响.不同仪器展宽Δνin下,Ad积分面积随XL变化关系相同的,使用三次多项式对理论计算的非线性曲线进行拟合得
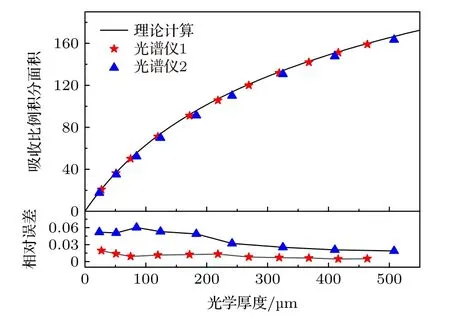
图13 吸收分数积分面积随光学厚度变化规律Fig.13.Dependence of integral area of absorption fraction on optical thickness.
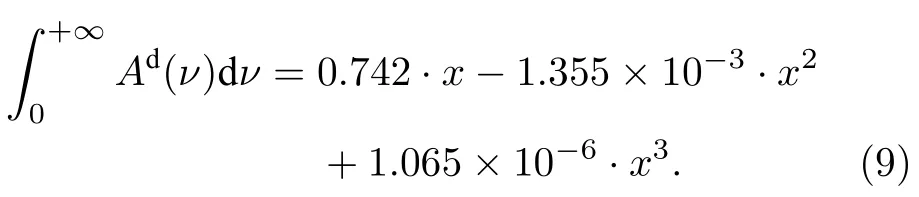
由于积分面积不受φin(ν)影响,不同仪器测量光谱的积分面积均可用(9)式描述,为面积法的改进与创新提供参考数据.
5 结论
NO 作为重要污染物,由于其紫外宽带光谱的结构特点,非线性问题十分严重,给实际测量带来极大干扰.本文对NO 吸收率峰值与吸收分数积分面积随光学厚度的非线性变化问题进行理论和实验研究,可以总结为以下6 个方面.
1) 研究单谱线吸收率峰值的非线性行为,分析吸收率峰值非线性度随仪器展宽的变化规律;发现当仪器展宽接近谱线真实展宽时,仪器展宽改变对非线性行为的改变最大.
2) 计算不同仪器展宽下NOγ(0,0)谱带吸收率峰值峰的非线性行为,给出其多项表达式并对一次项、二次项系数与非线性度随仪器展宽的变化规律进行分析,发现NO 的非线性度并不随仪器展宽单调递增,其变化过程可分为三个部分: 当Δνin<0.018 nm 与Δνin> 0.066 nm 时,非线性度随仪器展宽增加.而0.018 nm< Δνin< 0.066 nm 时,非线性度随展宽增大而减小.
3) 建立描述不同仪器展宽下NOγ(0,0)谱带吸收率峰值非线性行为的多项式系数数据库,提供了一种更加简便的基于插值多项式的NO 浓度测量方法.
4) 计算并比较NO 不同振动谱带吸收率峰值与吸收分数积分面积的非线性行为.发现在消除吸收强度的影响后,弱吸收时不同谱带间非线性行为差异较小,并且相比于吸收率峰值,不同谱带间积分面积变化行为的差别更小.
5) 使用两台光谱仪实验测量了不同浓度下NO 的吸收光谱并与理论计算结果进行对比.吸收率峰值非线性行为的相对误差小于4%,积分面积的相对误差小于6%,证明理论计算的准确性.峰值实验结果与数据库插值多项式之间的相对误差小于 8%,证明数据库的可靠性.
6) 提供了NOγ(0,0)谱带吸收分数积分面积随光学厚度变化的三次表达式,为面积法的改进与创新提供参考.
附录
表A1 不同仪器展宽Δνin 下多项式系数Table A1.Polynomial coefficients in different Δνin.
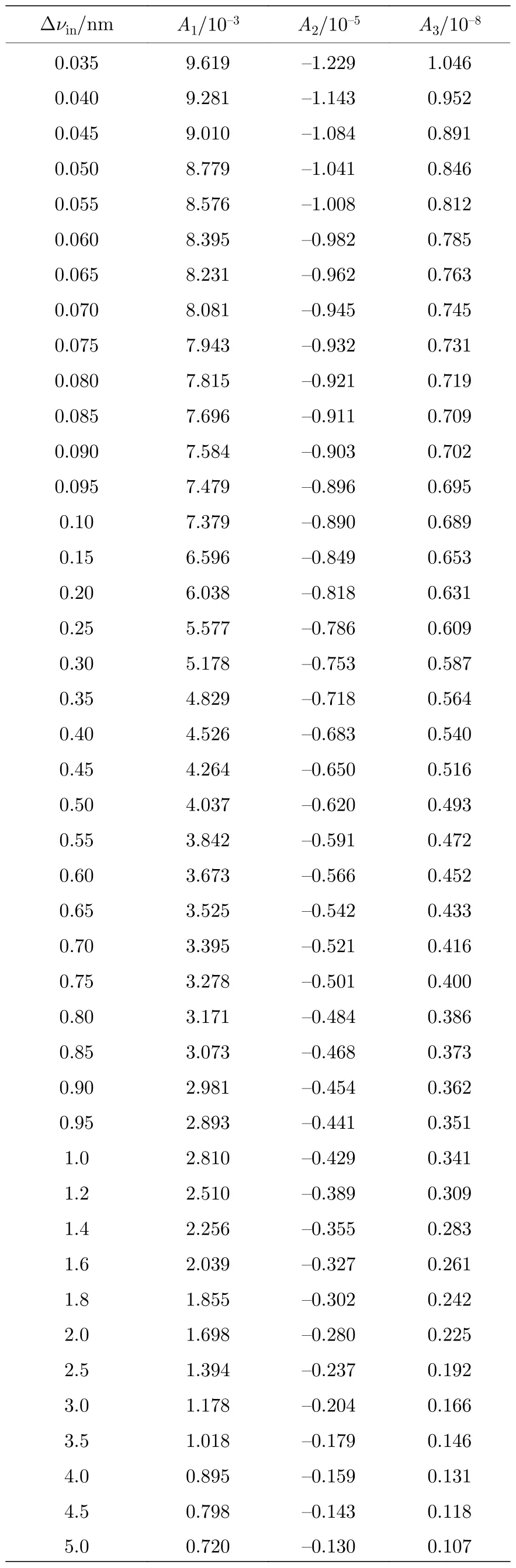
表A1(续)不同仪器展宽Δνin 下多项式系数Table A1 (continued).Polynomial coefficients in different Δνin.
