珠链喷泉原理模型

2022-10-26龙春晖陈梦妮马力果

湖南理工学院学报（自然科学版） 2022年4期

罗良,龙春晖,杨翔,陈梦妮,马力果,钱坤

(1. 湖南理工学院物理与电子科学学院,湖南岳阳 414006; 2. 岳阳市第九中学,湖南岳阳 414000)

0 引言

一条足够长的珠链有序地堆叠在一个容器内,给予其悬挂于容器外的部分一个合适的初速度,珠链在重力作用下会逐渐加速下落,当速度增加到足够大时,珠链即可飞跃起来,这就是珠链喷泉实验(见图1). Herrmann[1]等用动量流与能流对珠链喷泉现象进行分析,得出珠链喷泉最大高度为H0,最大速度为v2= 2gH0(H0为杯子距离地面高度). 夏艳[2]等构建由两段直线与一段半圆组成的珠链喷泉稳定状态模型,分析珠链飞起高度的数值关系. 国内外学者大多认为珠链向上飞跃的推力来源是珠链两小球与杆组成的基本结构在转动过程中杯子给予其的反作用力[1～7]. 在进一步考虑珠链大小、距地高度和用绳子代替珠链进行的珠链喷泉扩展实验时,发现一些奇特的实验现象(见图2),即无珠链基本构造的绳链也可展现出同样的喷泉现象. 本文将从相互作用力与惯性的角度出发,建立珠链喷泉模型.对珠链运动中的类稳态问题采用微元法进行分析,建立非半圆轨迹模型,并利用录像取帧技术[8]进行数据采集,以验证模型的正确性.

图1 珠链喷泉

图2 绳链的喷泉现象

1 珠链喷泉物理原理

通过实验观测,发现珠链喷泉具有以下几个性质:

(1)在珠链总长度(L总)与杯子离地高度(H地)相同的前提下,线密度越大的珠链飞得越高(见图3).

图3 珠链线密度越大则飞得越高

(2)在L总与珠链线密度相同的前提下,H地越大则珠链飞得越高(见图4).

图4 H地越大则飞得越高

(3)在珠链线密度与H地相同的前提下,杯内剩余珠链的数量越多则飞起的高度越高(见图5).

图5 杯内剩余珠链越多飞得越高

(4)在珠链离开杯子的最后一小段其飞跃的高度会突增(见图6),绳子也有同样的情况.

图6 最后一小段高度突增

(5)当杯子离地高度H地不变,且杯中有足够多的珠链时,珠链最高点超过杯口高度(h)基本不变.

根据性质(5),珠链喷泉存在一个类稳态阶段,在该状态下整条珠链的速度、轨迹不变,并以此建立非半圆模型.

在类稳态下,珠链形状不变,可以看成一个个微元按照既定的轨道运动,因此分析一个微元的运动即可推出整体珠链的运动状态.在腾空的珠链中选择任意微元进行受力分析(见图7),其中微元的质量为m=M/L,此即珠链的线密度.

图7 受力分析

在类稳态下整条珠链的速率相同且不变,故根据牛顿第二定律得

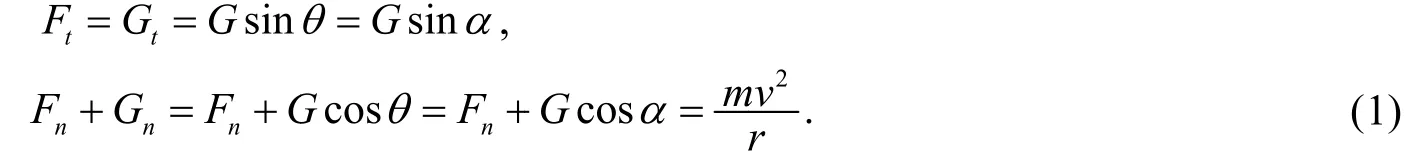
其中Ft、Fn、Gt、Gn为该微元所受切向力和法向力,r为轨迹曲率半径,θ取顺时针为正.

法向力Fn是一个未知函数,且无法从实验测得.仔细观察珠链的结构不难发现,当珠链慢慢弯曲时,随着弯曲程度增大,需要的力越大.因此珠链间的作用力,也随着弯曲程度的变化而变化,且随着曲率半径的增大而减小.假设类稳态中法向力的形式为Fn=a/rn.其中a,n为常数,且都只与珠链本身有关.本文考虑n=1,n= 2两种情况,a由实验数据拟合计算得出.

情况1:Fn=a/r

根据法向力假设,式(1)可进一步写成

曲率半径表达式为

利用函数一阶导数的几何意义(y＇=tanθ)与三角函数恒等式,联立式(2)和(3),积分得

θ= 0时,对应最大飞跃高度,即

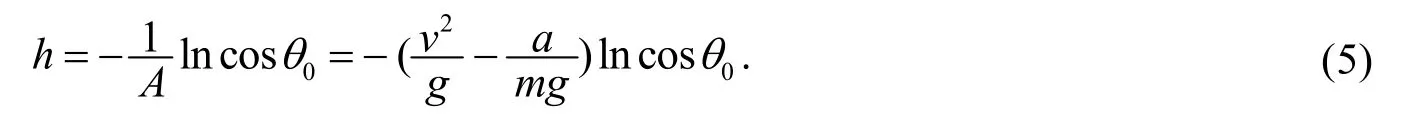
经过大量实验观察发现,θ0都接近 π /2,故 ln cosθ0＜ 0. 对式(5)进行分析可知,速度越大则跃起的高度越高; 若a＞ 0则质量越大的珠链跃起的高度越高. 式(5)最大高度的关系式对实验有指导作用.

情况2:Fn=a/r2

讨论更为一般的法向力,根据向心力公式有

取n=2,联立式(3)和(6),化简可得高度与角度的直接关系:

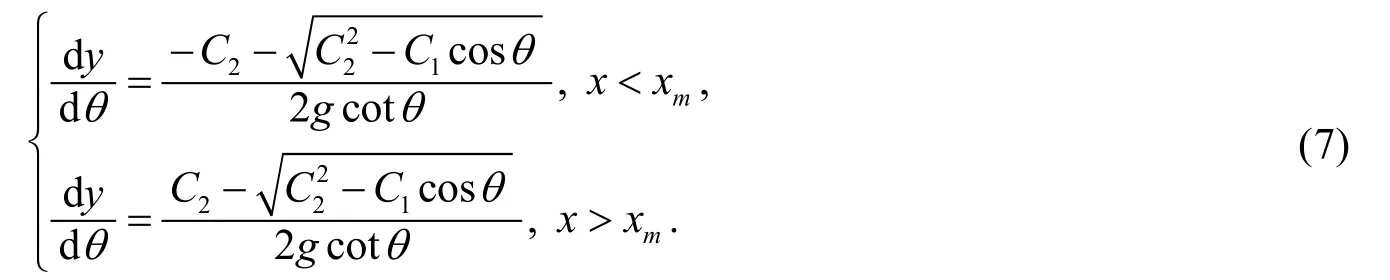
其中C2=v2,C1= 4ga/m.

2 实验验证

设置合适的背景(刻度板),利用手机对珠链喷泉进行慢动作录像,再使用视频截屏软件PR 对录像进行处理以测量最大飞跃高度与速度等参数,用电子秤和卷尺测量线密度.

(1)Fn=a/r时的参数拟合与误差分析

将实验中得到的各数据代入式(5)中,计算结果见表1. 其中h为杯口到顶点距离,h1为杯内静止部分珠链到顶点距离,取θ0= 87.75°.

表1 实验数据与结果

从表1可以看出,用h1计算的a1值与h计算的a值相差较小.为了方便读数与测量,下文的实验分析采用a值进行分析.取a=0.4503,回代入式(6).图8为模拟珠链轨迹和珠链实际轨迹对比图,图9 为珠链实际轨迹照片,图10为相对误差图.可见计算值与实际测量值的误差在5%以内.

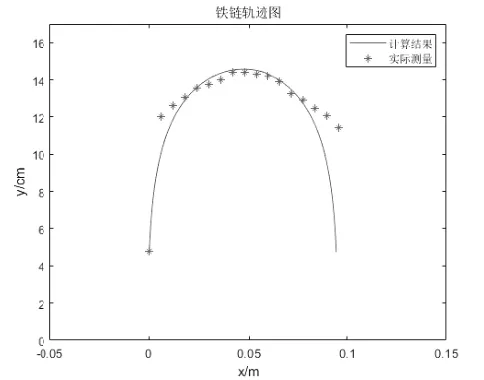
图8 计算值与实际值比较

图9 实际轨迹

图10 误差分析

(2)Fn=a/r2时的参数拟合与误差分析

根据式(7),取参数a=0.0318,y0=0.075m代入式(7)进行数值积分,绘制误差图和轨迹图,如图11和图12所示.

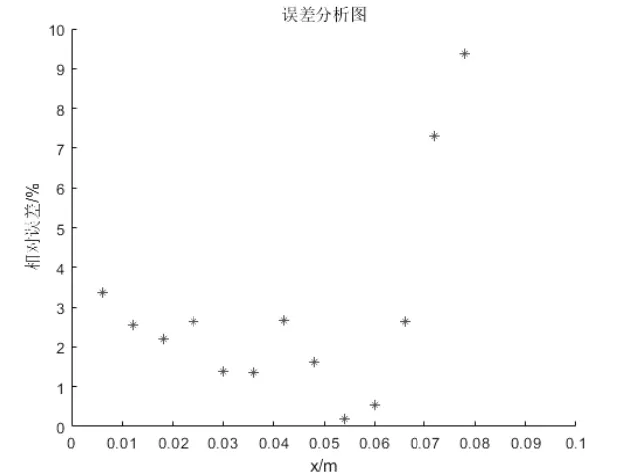
图11 金色珠链误差

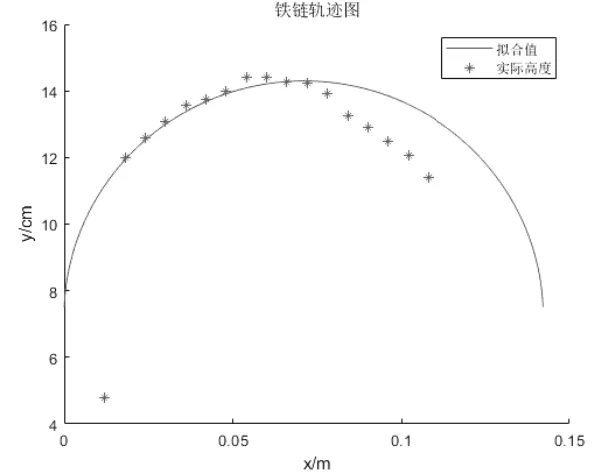
图12 金色珠链轨迹

分别分析不同法向力情况下的误差,误差大部分在3%到5%以内,因此本模型可以很好地解释珠链喷泉现象.由公式可知,珠链最大飞跃高度与珠链速度和线密度成正比.珠链最大飞跃高度还与杯子距离地面高度成正比,因为距离地面高度越高,则珠链加速时间越长,达到类稳态时速度越大,从而飞跃高度越高.杯内剩余链条数量越多,则处于稳态时间越长,比珠链数量少(在运动过程中还未达到稳态就已结束)的速度大,故飞跃高度越高.当最后一段珠链飞出杯口时,法向力常数发生突变,故高度会发生突变.至于绳子为何可以飞跃一定高度,可能是因为绳子的质量较小,运动过程中速度较大,由于惯性的原因飞起了一定高度.