预制超高性能组合式夹心墙板受压承载力研究

刘运林，郝北京，王子恒，黄 潇，王冬花，康 星

(1.安徽建筑大学 土木工程学院，安徽 合肥 230601；2.安徽审计职业学院，安徽 合肥 230601;3.安徽省装配式建筑研究院，安徽 合肥 230601；4.安徽晶宫绿建集团有限公司，安徽 阜阳 236000)

装配式建筑中非组合式墙板虽然受力明确，设计简单，但是墙板在受力时外叶墙板和内叶墙板是独立工作的，仅内叶墙板承受荷载，外叶墙板作为保护层和装饰层不承受荷载[1]。在建筑设计中，为了满足承载力和变形要求，内叶墙板厚度通常设计较大，导致墙体自重增加，因此会使结构的抗震性能下降[2]。

国内外学者对夹心保温墙板做了大量的研究，Junsuk等对夹心保温墙板在均布荷载作用下的响应进行了数值模拟[3]，通过与试验对比验证了数值分析的可行性与准确性。Joseph等对6种不同工况下的夹心墙板进行试验研究[4]，得出结论在没有夹心层或夹心层-面层之间粘结力丧失的情况下，连接件的存在可以提高墙板的复合作用程度。黄远等对三明治保温夹心外墙挂板进行了拟静力试验[5]，结果表明：含有三明治夹心保温墙体的外墙挂板框架的刚度提高了约20%。

图1 预制超高性能组合式夹心保温墙板示意图

目前夹心保温板仍存在内外叶墙板无法共同受力和对连接件与墙板的连接性能、抗剪强度要求较高等问题，因此本文采用分层成形的思路，提出了一种预制超高性能组合式夹心保温墙板，如图1所示。由于超高性能混凝土(UHPC)强度较高，内外叶墙板采用超高性能混凝土浇筑，可以改善墙板的延性、提高墙板的耗能能力和耐高温性能[6]。泡沫混凝土阻燃性好，具有良好的耐高温性能[7]，采用泡沫混凝土作为保温层材料可以避免冻融循环对保温层粘结力的影响[8]，实现墙体保温材料与建筑结构同寿命。

为了研究预制超高性能组合式夹心保温墙板的力学性能，本文利用ABAQUS对此类墙板的受压性能进行了数值模拟，拟合了稳定系数的计算公式，可用于墙板受压承载力的计算。

1 ABAQUS有限元模型

1.1 有限元模型的验证

Benayoune等对不同高厚比夹心墙板进行了轴心受压、偏心受压和弯曲荷载试验[9]，并对荷载作用下墙板的挠度和极限荷载进行了有限元分析，为本文提供了研究思路。为了保证ABAQUS模型的合理性和准确性，根据文献[9]建立部件的尺寸和材料参数见表1。

表1 文献中的部件尺寸[9]

利用ABAQUS软件根据参考文献中实际尺寸建立有限元模型[9]，墙板采用的单元类型为C3D8R，钢筋采用的单元类型为T3D2桁架单元，夹心层不计入受力分析[10]。为了使数值模拟更加接近实际情况，设置了初始缺陷来模拟试件生产、运输和安装过程中带来的不可避免的缺陷和误差。

先模拟出墙板的一阶屈曲模态[11]，然后修改模型关键字“*IMPERFECTION”以达到引入初始缺陷的目的[12]。上下面分别耦合在中心位置，在耦合点处施加边界条件和载荷。

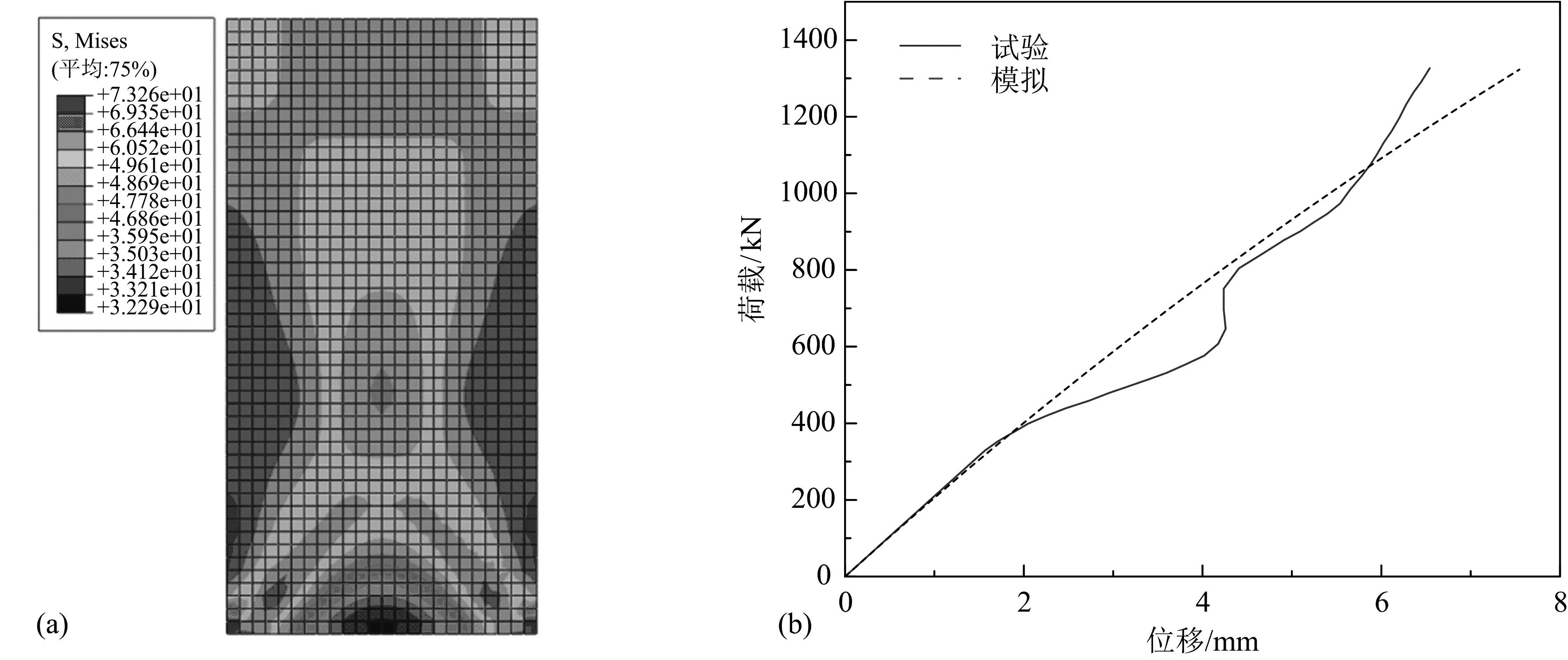
图2 文献中PA3墙板承载力应力云图及荷载—位移曲线的试验值与模拟值对比图[9]

文献[9]中PA3墙板承载力应力云图及荷载—位移曲线的试验值与模拟值对比图如图2所示，其他墙板的有限元模拟值与试验值的对比见表2[9]。6组数据之间的误差均在7%以内，证明了有限元模型的准确性和假设的合理性。

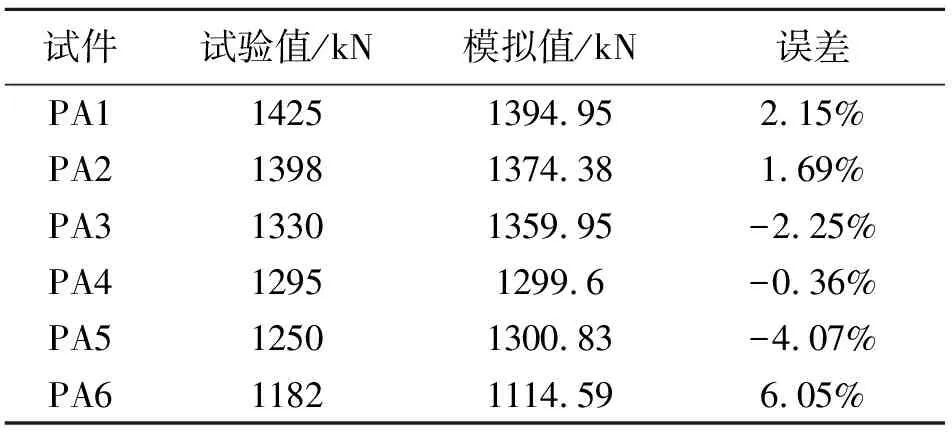
表2 数值模拟结果与试验值对比

1.2 预制超高性能组合式夹心保温墙板模型概况

根据实际工程中常用的墙板高度，本文设计的墙板高度分别为2800、3200和3600 mm，墙板宽度均为1200 mm，墙板总厚度为200 mm(内外页墙板厚度为50 mm，保温层厚度为100 mm)和250 mm(内外页墙板厚度为75 mm，保温层厚度为100 mm)两种厚度。试件编号和尺寸见表3。

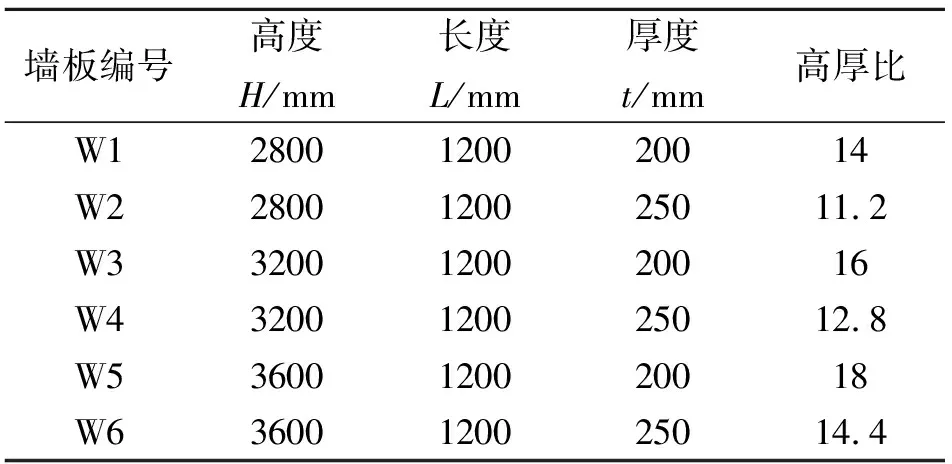
表3 试件标号和尺寸

内外页墙板均采用超高性能混凝土，墙板的横向分布钢筋和竖向分布钢筋均为直径为8 mm的HRB400钢筋，钢筋间距为150 mm。

混凝土面层、EPS保温板和GFRP格栅连接件采用C3D8R单元；钢筋和GFRP棒式连接件均采用T3D2单元，在MESH模块中，混凝土面层网格划分如图3所示，将墙板面层、夹心保温层网格划分为30 mm，连接件(GFRP棒状和格栅连接件)网格大小为20 mm，钢筋网片网格大小为10 mm。

由于钢筋与混凝土之间连接可靠，GFRP棒式连接件和GFRP格栅式连接件强度基本相同，连接可靠，因此假设钢筋、GFRP棒式连接件和GFRP格栅式连接件与混凝土之间没有相对滑移，钢筋、GFRP棒式连接件和GFRP格栅式连接件与混凝土之间约束关系选择Embedded Region[13]；EPS保温板与混凝土之间粘结效果较好，且不考虑EPS保温板承受荷载能力[14]，将EPS保温板和超高性能混凝土面层采用Tie约束；墙板面层与泡沫混凝土夹心层的接触设置为：法向行为设置为“硬”接触；切向行为设置为“罚摩擦”，黄成林和叶海登建议墙板面层与泡沫混凝土的摩擦系数分别为0.8和0.9[15-16]，为了安全起见，本文取摩擦系数为0.6[17]。通过以上不同材料之间的接触设置，以实现力在不同材料之间的传递。

数值模拟中采用位移加载，即在墙板上表面参考点施加竖向位移。墙板的一阶屈曲模态如图4所示，为了模拟实际工程运输、安装过程中造成的墙板缺陷，将墙板一阶屈曲模态的幅值设置为墙板高度的1/1000作为初始缺陷。

图3 混凝土面层网格划分

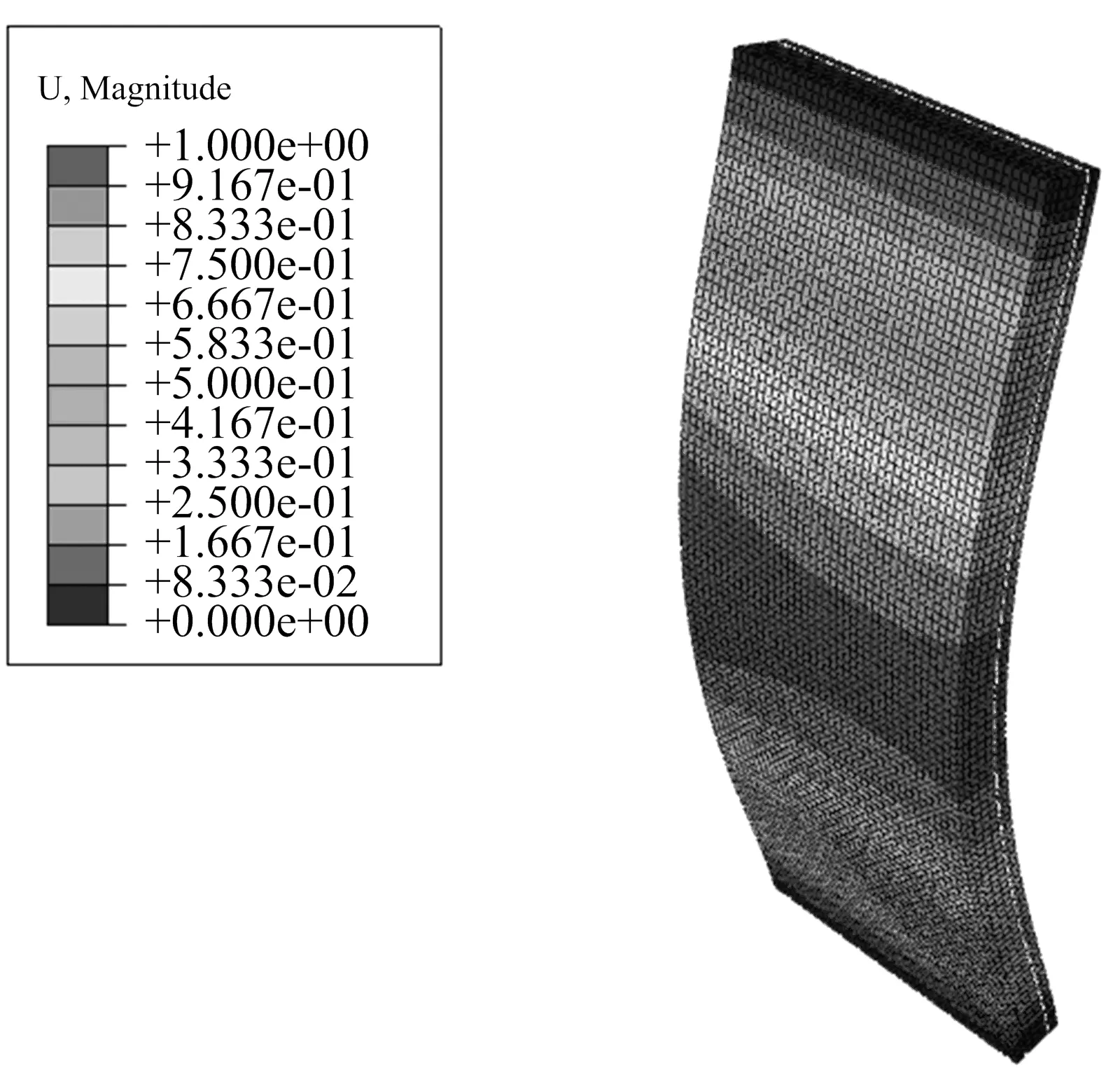
图4 墙板的一阶屈曲模态

2 数值模拟分析

2.1 工况设计

本文根据6个不同高厚比的墙板进行参数设计与分析，参数主要为：连接件类型、夹心层材料、墙板的约束方式和混凝土强度等级。详细参数见表4。G1—G4、G9—G11约束方式为两端铰接，G5—G8、G12—G14的约束方式为固结；G1—G8的面层材料为超高性能混凝土，G9—G14的面层材料为普通混凝土。

2.2 数值模拟结果

基于表4中14种工况的数值模拟结果如表5所示。

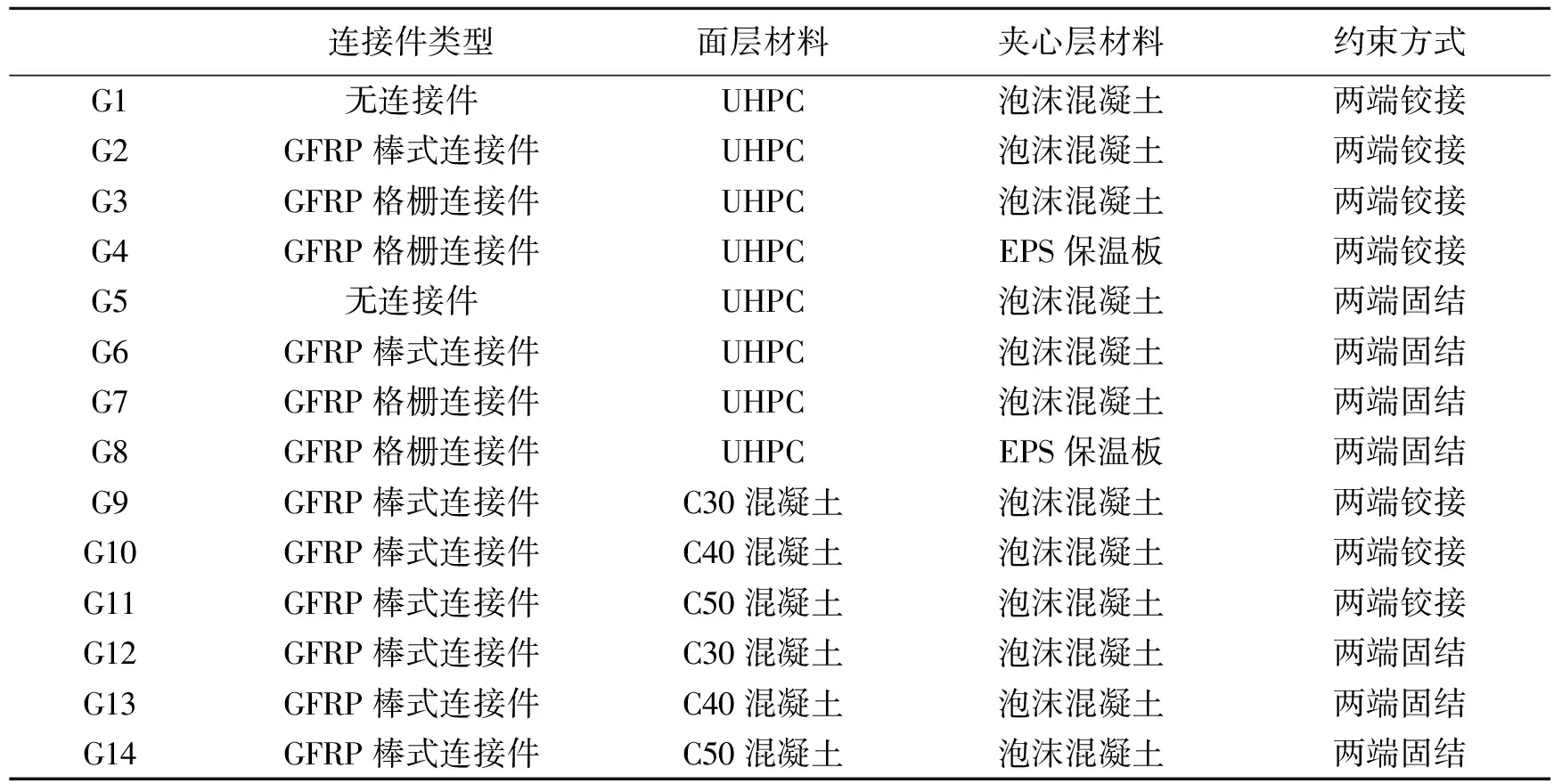
表4 数值模拟主要参数

表5 含有初始缺陷的墙板的极限承载力

2.3 参数分析

2.3.1 边界条件

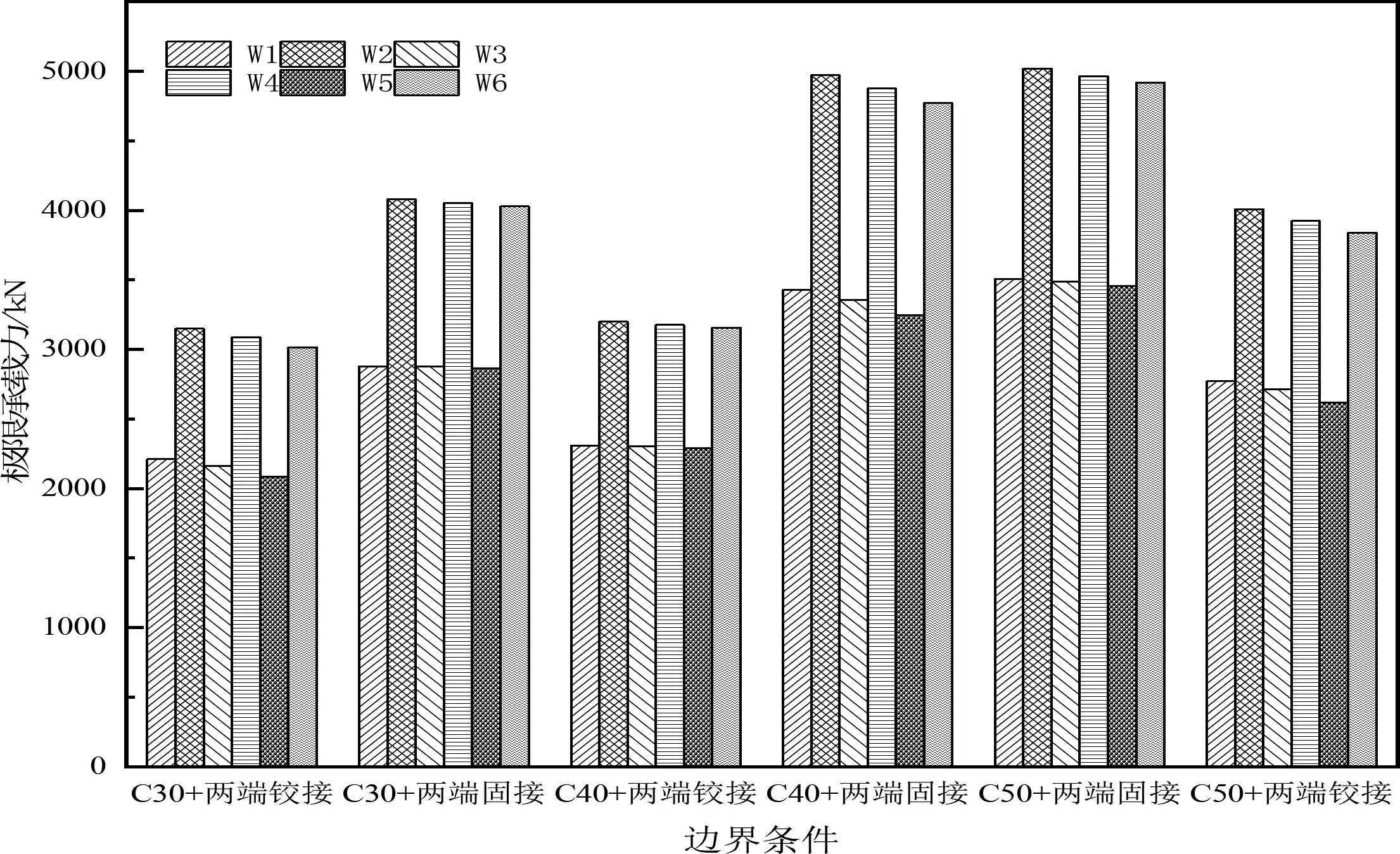
图5 不同边界条件下墙板的极限承载力

图5给出了W1—W6墙板在不同工况即不同边界条件下的极限承载力，G9—G11工况的边界条件为两边铰接，G12—G14工况的边界条件为两边固接，由图5可知不同边界条件对于墙板的极限承载力影响较大，两端固结墙板的极限承载力比两端铰接墙板的极限承载力平均提高了30.1%，这是因为边界条件实际控制着墙板的计算高度，从而影响了墙板的高厚比。

2.3.2 夹心保温层材料

不同夹心保温层材料对W1—W6墙板的极限承载力的影响如图6所示，G3和G7工况的墙板的夹心保温层材料为泡沫混凝土，G4和G8工况的墙板采用EPS保温板作为夹心保温层，由图5可知，泡沫混凝土作为夹心保温层的墙板较EPS保温板的墙板的极限承载力平均仅提高6.3%。同时由于泡沫混凝土和EPS保温板的抗压强度和刚度均低于超高性能混凝土抗压强度和刚度的5%[18,19]，夹心层材料对于墙板承载力的强度贡献较小，因此在数值模拟和理论计算时可以忽略夹心层的强度贡献。

图6 不同夹心保温层材料对墙板的极限承载力的影响

图7 不同面层材料对墙板的极限承载力的影响

图8 连接件形式对墙板的极限承载力的影响

2.3.3 面层材料

图7给出了W1—W6墙板在使用不同面层材料后的极限承载力，G9—G11工况的墙板使用的是C30—C50普通混凝土，G2和G6工况的墙板采用的是超高性能混凝土。从图7可以看出，当墙板边界条件为铰接或固结时，采用超高性能混凝土的墙板极限承载力较采用C30、C40和C50混凝土的墙板极限承载力均有明显的提升效果，极限承载力平均分别提升了228%、159%和111%。这是因为超高性能混凝土的抗压强度标准值能够达到120 MPa以上，因此超高性能混凝土夹心墙板的轴心受压承载力远大于普通混凝土夹心墙板，因此当设计受压承载力相同时，使用超高性能混凝土可以大幅度降低混凝土的使用量。

2.3.4 连接件形式

连接件形式对墙板的极限承载力的影响如图8所示，G2和G6工况的墙板采用GFRP棒式连接件，G3和G7工况的墙板采用GFRP格栅连接件，由图8可知，无论边界条件为两端铰接或两端固结，是否采用连接件及连接件的形式对于墙板的极限承载力影响不大。其中采用格栅连接件的墙板相比于采用棒式连接件的墙板的极限承载力提升了7%，这是因为格栅连接件能够形成一种空间结构体系，可以改善墙板稳定性并提高墙板的轴心受压承载力[20]。

2.3.5 高厚比

高厚比对墙板极限承载力的影响如图9所示。由图9(a)可知，当墙板厚度相同时，将20 0mm厚度的W1、W3和W5墙体和250mm厚度的W2、W4和W6在各种工况下的极限承载力对比发现，随着墙体高度的增加，即高厚比增加，墙体的极限承载力略有降低，降幅平均为5%以内。当墙板高度相同时，2800 mm厚度的W1和W2墙体和320 mm厚度的W3和W4以及3600 mm厚度的W5和W6在各种工况下的极限承载力对比如图9(b)所示，随着墙板厚度增加，即高厚比增加会显著提高墙板的极限承载力。这是因为墙板高厚比减小可以改善结构的稳定性，使混凝土受压面积增大，因此可以提高墙板的极限承载力[21]。

3 稳定系数修正

本文通过对以上不含初始缺陷的夹心保温墙板进行数值模拟，得到墙板的平面内的承载力结果如表6。

图9 高厚比对墙板极限承载力的影响

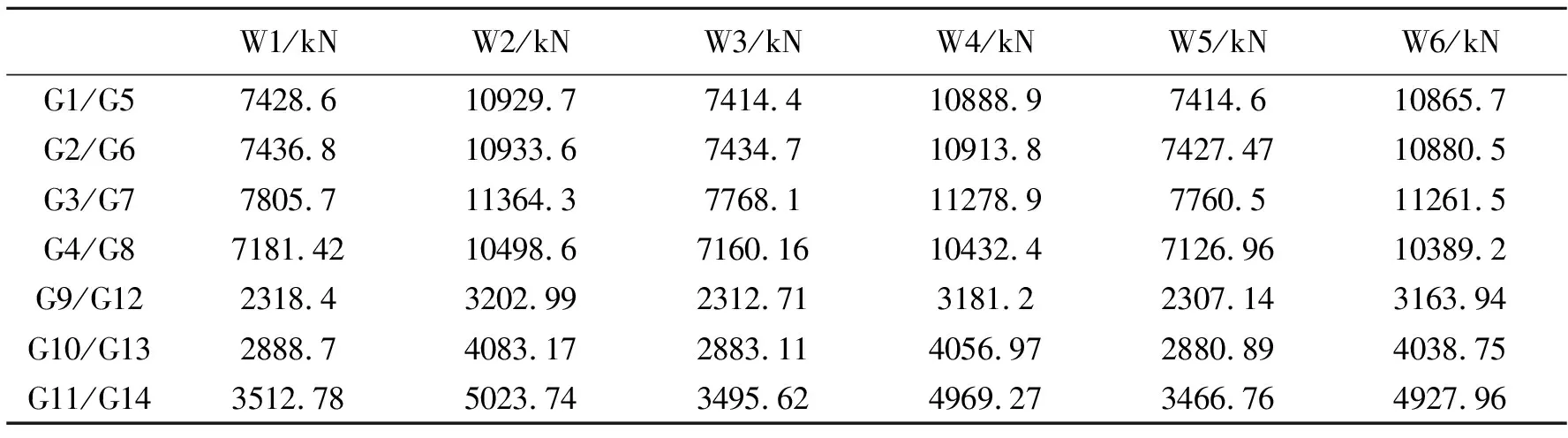
表6 墙板平面内承载力结果

3.1 对《混凝土结构设计规范》中稳定系数修正

《混凝土结构设计规范》(GB 50010-2010)中[22]，墙板的轴心受压承载力计算公式如下：

N=0.9φ(fcA+A′sf′y)

(1)

式中：φ—钢筋混凝土受压构件的稳定系数。

当纵向普通钢筋的配筋率大于3%时，公式中的A应改用(A-A′s)代替考虑到实际工程运输、安装过程中会造成墙板初始缺陷，为了拓展《混凝土结构设计规范》中轴心受压承载力计算公式的适用范围，将含有初始缺陷的墙板受压极限承载力与墙板平面内承载力的比值定义为夹心墙板的稳定系数的修正值φ1，具体数值见表7。

表7 夹心保温墙板稳定系数修正值φ1

由表7可知，墙板中连接件的类型和夹心层材料对于墙板的稳定性影响较小，这是因为两种连接件强度基本相同，连接可靠，夹心层材料强度远低于超高性能混凝土的强度[10]，因此墙板中连接件的类型和夹心层材料对墙板的稳定系数修正值φ1的影响不明显。所以建立只包含且适用于超高性能混凝土材料的稳定系数修正公式。

表7模拟的是两种边界条件(两端铰接和两端固结)的稳定系数修正值φ1，为了模拟工况的完整性，又进行了边界条件为：一端固定、一端铰支和一端固定和一端自由两组共23种工况下稳定系数修正值的模拟φ1。结果见表8。

表8 稳定系数修正值的模拟值

图10 高厚比对稳定系数φ的影响

由表8可知，墙板的高厚比对墙板的稳定系数修正值φ1有着显著影响，为了探究墙板的高厚比和墙板的稳定系数修正值φ1之间的关系，根据表8得到的稳定系数修正值φ1进行拟合，建立了墙板高厚比与稳定系数修正值之间的函数关系。高厚比—稳定系数拟合函数的图像和参数如图10(a)所示。为了更符合实际工程中的墙板规格，将高厚比小于8的模拟值略去以提高拟合的精度，得到的拟合函数的图像和参数如图10(b)所示，此时稳定系数修正值φ2拟合公式如式(2)：

φ2=ln(3.176-0.051l0/b)

(2)

注：φ2≤1且8≤l0/b≤36

对于8≤l0/b≤36的预制超高性能组合式夹心保温墙板，将稳定系数φ2代入《混凝土结构设计规范》(GB 50010—2010)中的计算公式[22]，得到墙板的轴心受压承载力计算公式如下：

N=0.9φ2(fcA+A′sf′y)

(3)

式中：φ2—修正后钢筋混凝土墙板受压构件的稳定系数，按式(2)计算。

当纵向普通钢筋的配筋率大于3%时，公式中的A应改用(A-A′s)代替。

将上述公式的计算值和数值模拟的结果对比如表9。

表9 公式值和数值模拟值对比

由表9可知：拟合公式计算结果较符合模拟值结果，可以较准确地计算出预制超高性能组合式夹心保温墙板的轴心受压承载力，为工程实践提供参考。

4 结论

本文研究设计了一种预制超高性能组合式夹心保温墙板，并采用ABAQUS有限元软件模拟了墙板在轴压下的承载力和破坏形态，分析了边界条件、夹心层材料、面层材料、连接件形式和高厚比等参数对墙板受压承载力的影响规律，得到承载力稳定系数，提出墙板的受压承载力计算公式。本文得到的主要结论如下：

(1)引入初始缺陷对墙板进行受压模拟发现：当墙板厚度相同时，随着墙板高度增加，即高厚比增加会使墙体的受压极限承载力平均降低5%，当墙板高度相同时，随着墙板厚度增加，即高厚比减小会改善结构的稳定性，显著提高墙板的极限承载力。

(2)不同墙板面层材料显著影响了墙板的极限承载力，采用超高性能混凝土的墙板受压极限承载力较采用C30、C40和C50混凝土的墙板受压极限承载力平均分别提升了228%、159%和111%。

(3)墙板的边界条件对于墙板的受压极限承载力影响较大，两端固结墙板的极限承载力比两端铰接墙板的极限承载力平均提高了30.1%，而夹心层材料和连接件的形式对于墙板的受压极限承载力几乎无影响。

(4)将含有初始缺陷的墙板受压承载力与墙板的平面内承载力的比值作为夹心墙板的稳定系数，得到稳定系数的拟合公式φ=ln(3.176-0.051l0/b)(φ≤1)，将其代入受压承载力计算公式，得到超高性能组合式夹心保温墙板的建议计算公式。

(5)根据数值模拟结果和材料力学知识可知合理地设计墙板的高厚比及增强墙板端部的约束条件可以提高墙板的稳定性和轴心受压承载力。