降低电压暂降下负荷损失的低压脱扣装置参数优化
2022-10-26李昊桐秦博宇
王 康,李 骏,李昊桐,李 立,秦博宇
(1.国网陕西省电力公司调控中心,陕西 西安 710048;2.西安交通大学电气工程学院,陕西 西安 710049)
1 引言
低压脱扣装置作为断路器中的重要附件,具有低电压保护的功能,在现代电力系统中被广泛使用[1,2]。当主网发生电压暂降时可能导致大量低压脱扣装置动作,严重威胁电网的安全稳定运行,甚至引发大范围停电事故,造成巨大的经济损失[3]。由低压脱扣装置动作导致的失负荷事故在全国时有发生,引起了广泛关注。例如2008年6月13日,深圳电网220 kV妈岸乙线受雷击发生相间短路故障,故障引起大范围电压暂降,导致约600 MW的负荷因低压脱扣装置动作而损失[4];2014年7月8日,广东东莞220 kV莞景乙线发生B、C相间短路故障,电压暂降导致大量低压脱扣装置动作,损失负荷约1 012 MW[5]。因此,研究降低电压暂降下负荷损失的方法具有重要意义。
建立准确的负荷损失量化评价体系是研究降低电压暂降下负荷损失方法的基础。目前,国内外对负荷损失量化评价体系的研究已取得一定成果。文献[6]基于一次函数建立负荷损失量和电压暂降幅值之间的数学模型,分析事故的负荷损失量。该方法未考虑低压脱扣装置的动作特性,导致计算的负荷损失量误差较大。文献[7]通过电压暂降敏感特性实验绘制低压脱扣装置的电压耐受曲线,揭示低压脱扣装置在电压暂降作用下的动作特性。在此基础上,文献[8]将用户按照报装容量分类,基于低压脱扣装置的电压耐受曲线建立每类用户的负荷损失模型。此建模方法未考虑低压脱扣装置的参数配置,仍存在误差较大的问题。
在降低电压暂降下负荷损失的研究中,国内外学者提出了改进低压脱扣装置参数的方案。文献[9]提出对于受电压暂降影响较小的设备,应在低压脱扣装置增加延时元件,延时的设置应综合考虑电网切除时间和用电设备对电压暂降的承受能力。文献[8]提供了躲过重合闸时间的整定方案:第一,躲过变压器所在线路发生故障并重合闸的欠压时间;第二,躲过同一变电站母线的其他线路发生故障并重合闸的欠压时间。文献[10]提出基于电动机的惰行时间整定方案。出于保护要求,电动机停转前应保证低压脱扣装置不动作,而在停转时要求低压脱扣装置立刻动作。现有降低电压暂降下负荷损失的研究中,主要是对低压脱扣装置增加延时元件,但缺乏不同类型用户电压、延时整定值的详细设定方案。
首先,本文将基于低压脱扣装置在不同参数配置下的动作特性,建立负荷损失量化评价体系;其次,以经济损失最小为目标,建立低压脱扣装置参数优化配置模型;然后,研究求解参数优化问题的方法,求解优化问题得到低压脱扣装置的参数优化配置方案;最后,通过陕西省实际算例验证负荷损失量化评价体系的准确性及低压脱扣装置参数优化配置模型的合理性。
2 电压耐受曲线
电压耐受曲线主要用于描述设备对电压暂降的敏感程度,能够反映低压脱扣装置在电压暂降期间的动作特性[11,12]。文献[13,14]根据电压暂降敏感特性实验数据绘制了江苏国星、上海磊跃、浙江阿尔斯通、江苏凯帆和浙江正泰五款市面上常用低压脱扣装置的电压耐受曲线。以江苏国星和江苏凯帆为例,其电压耐受曲线如图1所示。
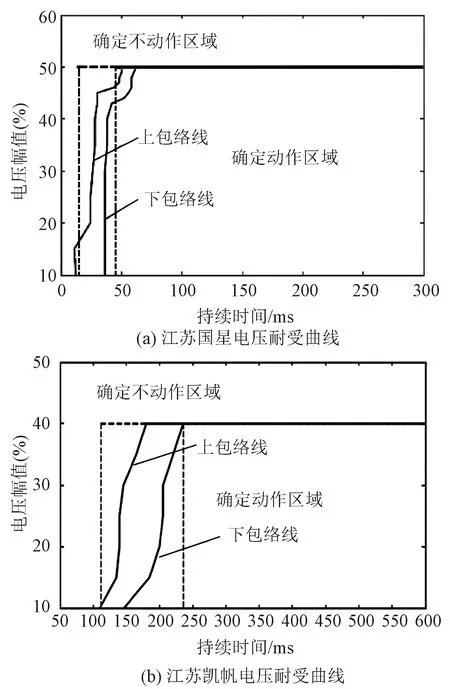
图1 电压耐受曲线
若低压脱扣装置端的电压处于图1中的不动作区域,则低压脱扣装置一定不动作;若处于图1中的动作区域,则低压脱扣装置一定动作;若处于图1中的模糊区域,则低压脱扣装置以一定概率动作。从图1可知,不同型号低压脱扣装置的电压暂降敏感性具有一定差异。为反映低压脱扣装置动作特性的整体情况,需汇总设定同一电压、延时整定值的低压脱扣装置型号,归并各型号低压脱扣装置的电压耐受曲线,归并原则为选取不动作区域与模糊区域最小的时间边界值作为综合电压耐受曲线不动作区域与模糊区域的时间边界值,选取动作区域与模糊区域最大的时间边界值作为综合电压耐受曲线动作区域与模糊区域的时间边界值。由此,绘制的低压脱扣装置综合电压耐受曲线如图2所示。图2中,Uset为低压脱扣装置的电压整定值;T1、T2分别为模糊区域与不动作区域、动作区域电压暂降持续时间的边界值。图2反映了各型号低压脱扣装置动作特性的整体情况,为建立负荷损失量化评价体系奠定了基础。
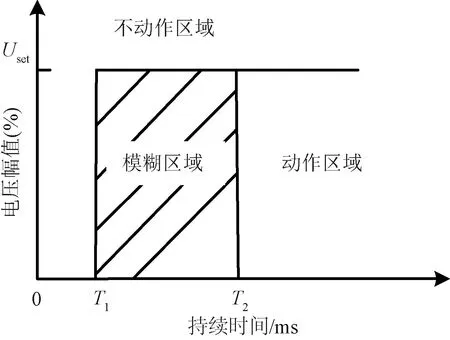
图2 低压脱扣装置综合电压耐受曲线
3 负荷损失量化评价体系
本节将基于低压脱扣装置综合电压耐受曲线,建立负荷损失量化评价体系。
首先,根据低压脱扣装置电压、延时整定值的设定情况将用户分类,通过每类用户的脱扣比例Cj计算变电站的负荷损失量Psag,即:
Psag=∑PCjkj
(1)
式中,kj为第j类用户负荷量占该站点总负荷量P的比例。
由式(1)可知,构建负荷损失量化评价体系的关键是求解每类用户负荷脱扣比例Cj。
其次,根据每类用户的低压脱扣装置电压耐受曲线求解负荷脱扣比例Cj。由图2可知,负荷脱扣比例Cj为一个分段函数。当低压脱扣装置端的电压暂降幅值和持续时间处于图2中的不动作区域时,Cj=0;若处于图2中的动作区域,则Cj=1;若处于图2中的模糊区域,则低压脱扣装置部分动作,因此还需确定模糊区域中负荷脱扣比例Cj。
因考虑到电压暂降幅值越低,低压脱扣装置动作的数量越多,为简化模型及分析,以简单的线性曲线描述模糊区域中负荷脱扣比例与广义上线路电压暂降幅值U的关系,即Cj=ajU+bj。综上,第j类用户的负荷脱扣比例函数Cj为:
(2)
式中,aj和bj为常数;Usetj为第j类用户低压脱扣装置电压动作整定值。由式(2)可知,当电压大于Usetj时,低压脱扣装置不会动作,由此可知模糊区域中一次函数的起始点为(Usetj,0),将此点代入Cj=ajU+bj中,可得bj=-ajUsetj。因此,式(2)中待求的未知参数仅为aj。最后,通过最小二乘法求解负荷脱扣比例函数Cj=ajU-ajUsetj中的未知参数aj。
将用户分为n类,设变电站i中第j类用户的负荷量占比为kij,在故障f下变电站i的电压暂降幅值为Ufi,电压暂降持续时间为tfi。Ufi为变电站电压而非用户端电压,需在Ufi前乘电压比例系数kv以代替用户整体的电压暂降幅值。由于不同变电站在故障f下的电压幅值不同,因此以Cij表示变电站i中第j类用户的负荷脱扣比例,将kvUfi和tfi代入式(2)中得到:
(3)
则变电站i的总负荷脱扣比例Cti为:
Cti=ki1Ci1+ki2Ci2+…+kinCin
(4)
设受故障波及的变电站数量为m,变电站i实际的负荷脱扣比例为Ctri,则负荷脱扣比例的偏差平方和S为:
(5)
为使偏差最小,将式(5)分别对aj求导,并令导数为0,即:
(6)
式(6)中,当Cij=0或Cij=1时,Aij=0。当Cij=ajkvUfi-ajUsetj时,Aij=kij(kvUfi-Usetj)。因此,为求出全部未知参数aj的值,选取的故障f应使得至少两个变电站的负荷脱扣比例函数Cij全部为n类用户模糊区域中的函数,且受故障波及的变电站数m≥2。
联立求解式(6),得到aj的值为aj*,bj的值为bj*。将aj*和bj*代入式(2)中,得到负荷损失量化评价体系。负荷损失量化评价体系为构建低压脱扣装置参数优化模型奠定基础,为验证低压脱扣装置参数优化配置方案提供数据支撑。
4 低压脱扣装置参数优化配置模型
本节将基于负荷损失量化评价体系,以经济损失最小为目标,建立低压脱扣装置参数优化配置模型,并采用萤火虫算法求解参数优化问题,得到低压脱扣装置参数优化配置方案。
4.1 目标函数
将用户按照第3节提出的分类方法进行分类,该分类定为用户的一级分类。在此分类的基础上,依据用户对电压暂降的敏感程度,对用户再次分类,该分类定为用户的二级分类。根据低电压运行及停电对每类用户的经济损失,建立以经济损失最小为目标的目标函数为:
(7)
式中,αu、βu、λu分别为第u类二级分类的用户因低压脱扣装置动作导致停电、低压脱扣装置未动作导致低电压运行和未安装低压脱扣装置导致低电压运行的经济损失系数;Pi为变电站i的负荷量;Cij为变电站i第j类一级分类用户的负荷脱扣比例;kiju为变电站i第j类一级分类中第u类二级分类用户的占比;M和F分别为变电站集合和故障集合;N和R分别为一级用户和二级用户类型的集合。
求取二级分类用户的比例kiju,即得到二级分类用户在一级分类用户中的比例,因此求解出kiju即得到二级分类用户的低压脱扣装置参数配置情况。
4.2 约束条件
电压暂降幅值及持续时间约束为:
(8)
用户比例约束为:
(9)
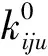
综合目标函数式(7)及约束条件式(8)、式(9),即为低压脱扣装置参数优化配置模型。
4.3 随机机会约束规划模型
模型中故障f是随机发生的,Cij和αu、βu、λu均与故障f下变电站的电压、持续时间相关,因此Cij和αu、βu、λu为随机变量,该优化问题为随机优化问题。为求解该优化问题,将模型转换为随机机会约束规划模型,转换后的目标函数为:
(10)
新增约束为:
(11)

因此,转换后的低压脱扣装置参数优化配置模型如下。
目标函数为:
(12)
约束条件为:
(13)
4.4 求解方法
为求解由式(12)及式(13)组成的低压脱扣装置参数优化配置模型,本节利用萤火虫算法对其求解,步骤如下:
(1)初始化算法基本参数。设置萤火虫种群个体数目V,初始最大吸引度β0,光强吸收系数γ,步长因子α0,最大迭代次数B,迭代次数num=0。
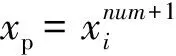
(7)输出全局极值点xp和最优个体值f(xp)。
5 算例分析
本节将以陕西省某地区因低压脱扣装置大范围动作,损失977.4 MW负荷的事故为例,验证负荷损失量化评价体系的准确性及低压脱扣装置参数优化配置模型的合理性。
5.1 负荷损失量化评价体系
5.1.1 事故数据
事故共造成六个330 kV变电站的负荷损失,变电站记为A、B、C、D、E、F,其变电站故障前的负荷量P及事故导致的负荷损失量情况见表1。

表1 变电站负荷损失情况
根据实际调研,该地区低压脱扣装置型号多数为杭申电气、浙江阿尔斯通、江苏凯帆和浙江正泰。低压脱扣装置延时时间每档间隔为1 s,延时时间设定多数在3 s以内,其电压整定值多数设定为0.4 pu、0.5 pu、0.6 pu。因此,按照低压脱扣装置参数配置情况可将用户分为13个类别(其中包括未安装低压脱扣装置的类别),每类用户的低压脱扣装置型号均为杭申电气、浙江阿尔斯通、江苏凯帆和浙江正泰。以变电站A为例,用户的分类及其比例见表2(参数配置表示方式为:{电压整定值,延时时间})。
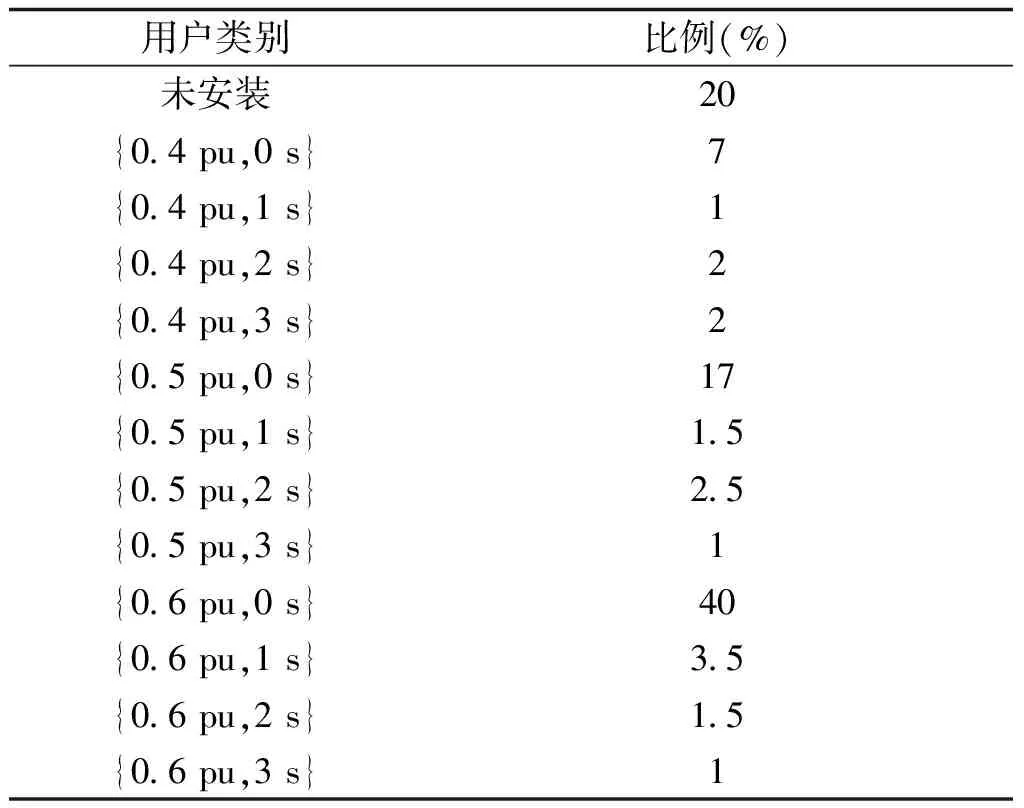
表2 变电站A用户的分类及负荷比例
5.1.2 评价体系的建立及验证
首先,按照第2节的方法绘制用户类型{0.4 pu,0 s}、{0.5 pu,0 s}及{0.6 pu,0 s}的电压耐受曲线如图3所示。其次,基于绘制的电压耐受曲线构建负荷损失量化评价体系,因增加延时的电压耐受曲线即将其无延时的电压耐受曲线沿时间轴向右平移对应的时间长度,因此,求出无延时的负荷脱扣比例函数,即可求出增加延时的负荷脱扣比例函数。
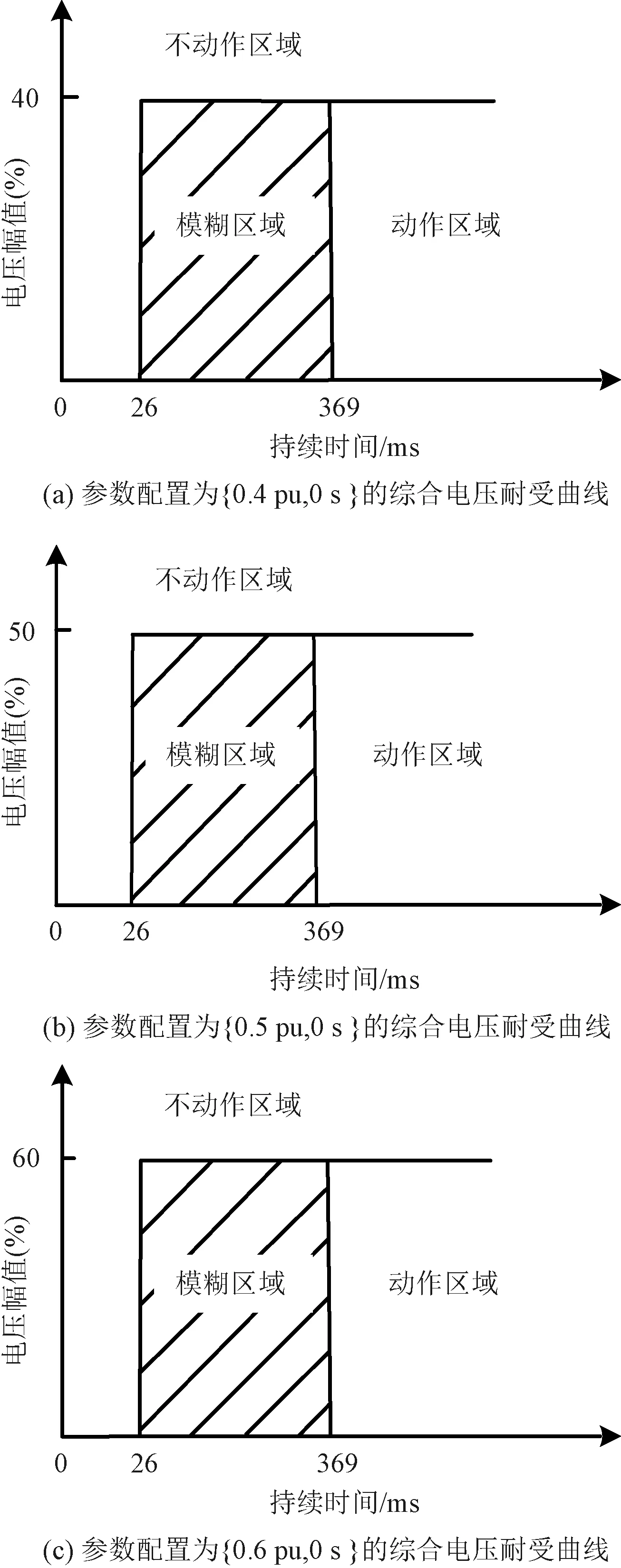
图3 陕西省低压脱扣装置综合电压耐受曲线
将变电站负荷实际损失比例Ctr、用户占比k、电压暂降持续时间t=68 ms、变电站A、B、C、D、E、F的电压暂降幅值UT={0.51,0.538,0.484,0.481,0.534,0.497}及电压比例系数kv=0.5代入式(5)和式(6)中。此外,用户类型{0.4 pu,0 s}、{0.5 pu,0 s}、{0.6 pu,0 s}初始点分别为(0.4,0)、(0.5,0)、(0.6,0)。
通过联立求解式(6),得到用户类型为{0.4 pu,0 s}、{0.5 pu,0 s}、{0.6 pu,0 s}的负荷脱扣比例函数为:
(14)
(15)
(16)
以{0.4 pu,1 s}为例,该类型的负荷脱扣比例函数即将{0.4 pu,0 s}的负荷脱扣比例函数向右平移1 s。因此,用户类型为{0.4 pu,1 s}的负荷脱扣比例函数为:
(17)
以此类推可得到其他增加延时的负荷脱扣比例函数,完成陕西省负荷损失量化评价体系的建立。
最后,将事故中变电站A、B、C、D、E、F的电压暂降幅值UT、电压比例系数kv、电压暂降持续时间t、负荷量P及用户占比k代入建立的负荷损失量化评价体系中计算此次事故的负荷损失量,通过对比各变电站的实际负荷损失量以验证负荷损失评价体系的准确性,结果见表3。结果证明构建的负荷损失量化评价体系具有较高精度。
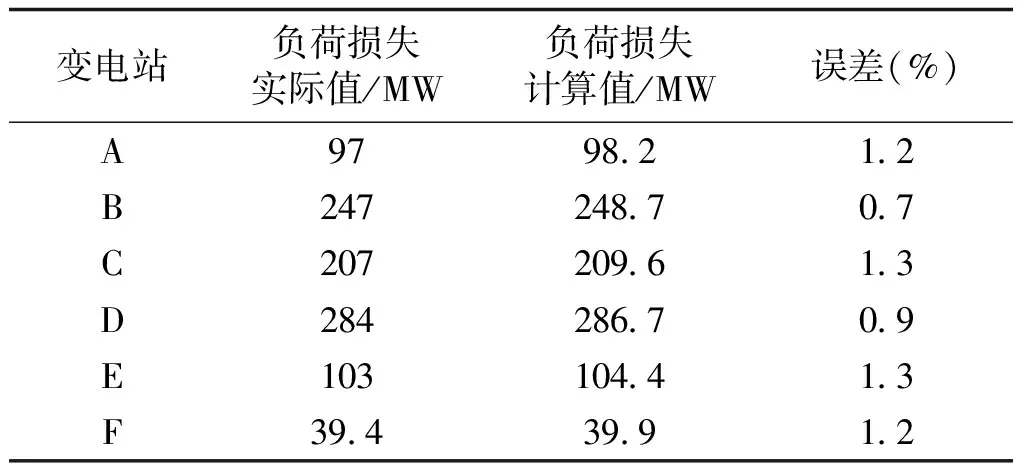
表3 变电站负荷损失计算值与实际值的对比
5.2 低压脱扣装置参数优化配置模型
首先,在5.1节中用户13个一级分类的基础上,结合实际调研的用户情况,根据用户对电压暂降的敏感程度和其停电及在低电压运行下的经济损失,将用户分为含精密仪器用户(如医院、高新技术企业等)、不含精密仪器的工业及其他(居民、酒店等)三类。根据实际调研,以变电站A为例,各用户所占变电站负荷量的比例见表4。

表4 变电站A各类型用户的负荷比例
根据调研各类用户在停电及低电压运行下的经济损失,制定每类用户的经济损失系数α、β、λ。因精密仪器内部装有低压脱扣装置,当电压暂降未引起低压进线端的低压脱扣装置动作时,其可能引起精密仪器内部的低压脱扣装置动作,从而造成经济损失。因此,在制定含精密仪器用户的经济损失系数时,需分情况讨论。根据实际调研结果显示,多数精密仪器内部的低压脱扣装置动作条件为电压暂降幅值低于0.7 pu,持续时间大于40 ms。因此,当电压暂降幅值U<0.7 pu,且持续时间t>0.04 s时,无论低压进线口处低压脱扣装置是否动作,含精密仪器用户将会因精密仪器内部低压脱扣装置动作而造成经济损失,从而构建此类情况的经济损失系数。而当电压暂降幅值U≥0.7 pu或持续时间t≤0.04 s时,含精密仪器用户内部的低压脱扣装置不会动作,根据低压进线口处的低压脱扣装置是否动作判断含精密仪器用户在此期间停电或低电压运行,从而构建此类情况的经济损失系数。制定的各用户经济损失系数见表5。

表5 经济损失系数
其次,按照式(12)和式(13)搭建陕西省低压脱扣装置参数优化配置模型,令模型中置信水平δ为0.9。利用Psasp软件模拟各种故障,记录各变电站故障期间的电压,并默认每个故障发生的概率相同。设置萤火虫种群个体数量V=600、最大吸引度β0=0.2、光强吸收系数γ=1,步长因子α0=0.25,最大迭代次数B=5 000,利用Matlab软件编写程序对该模型求解。以变电站A为例,结果见表6。
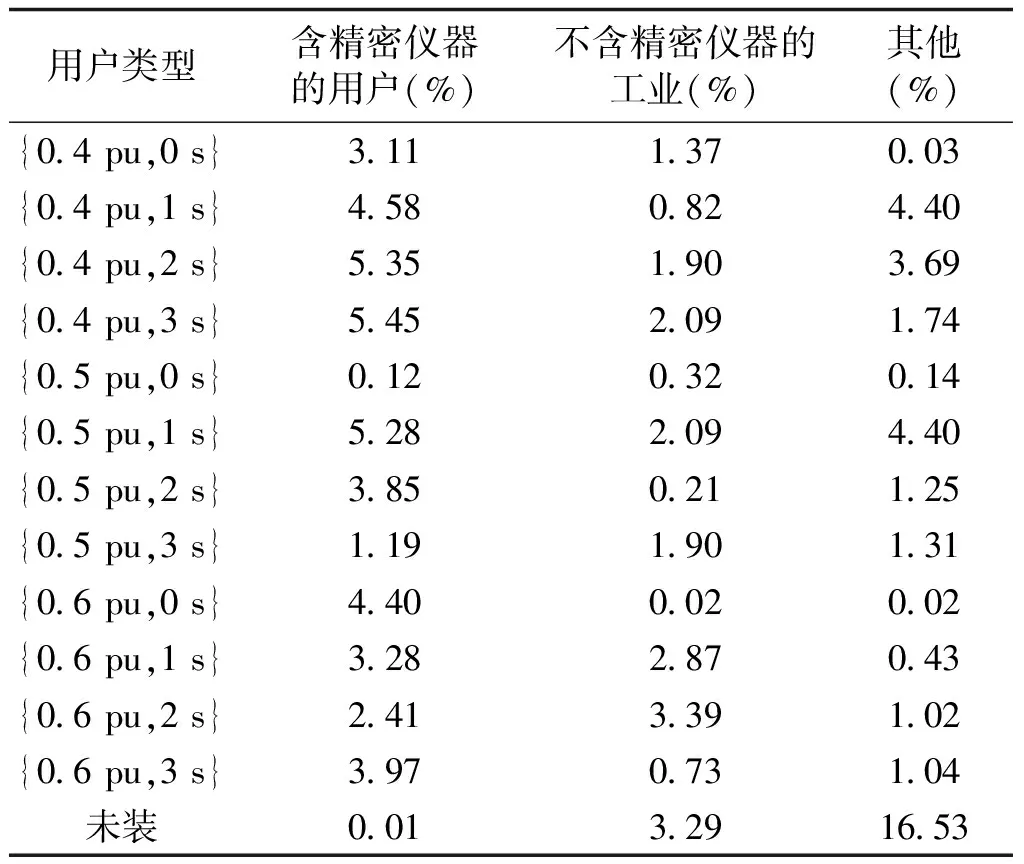
表6 变电站A各类型用户优化后的负荷比例
结果显示,相比优化前增加延时的用户比例16%,优化后增加延时的用户比例为70.64%,增加延时用户的比例增加了54.64%。未安装低压脱扣装置的比例从优化前的20%变为19.83%,其比例基本没变。
将数据代入陕西省负荷损失量化评价体系中计算优化后变电站的负荷损失量,结果见表7。
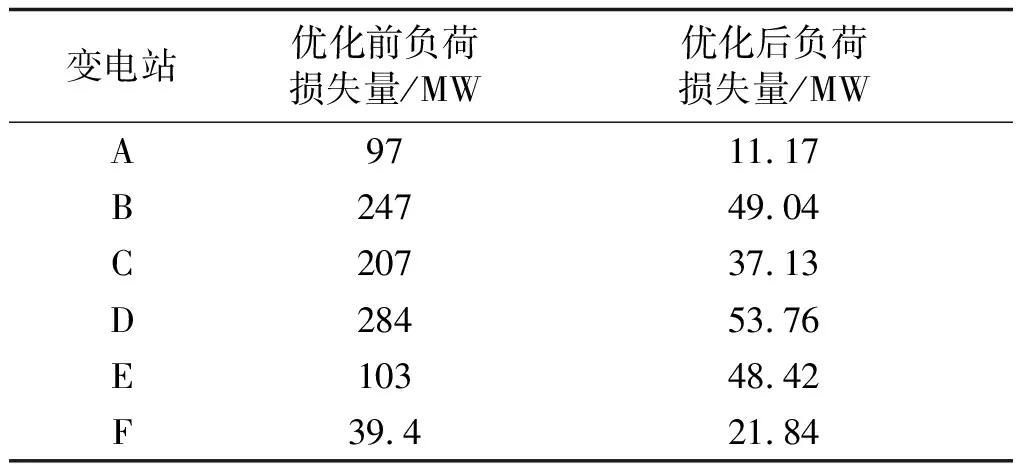
表7 优化后的变电站负荷损失量
优化后的方案总共损失221.36 MW的负荷,相比优化前损失的977.4 MW,总共减少756.04 MW的负荷损失。结果表明低压脱扣装置参数优化配置方案具有较好的效果。
6 结论
本文提出基于低压脱扣装置的电压耐受曲线,建立负荷损失量化评价体系的方法。并基于负荷损失量化评价体系,建立以经济损失最小为目标的低压脱扣装置参数优化配置模型,通过更改用户的低压脱扣装置电压、延时整定值,以减少电压暂降下的负荷损失量。通过分析陕西省实际案例得到以下结论:
(1)基于低压脱扣装置的电压耐受曲线,建立的负荷损失量化评价体系误差较低,具有较高精度。此外,其能够计算不同低压脱扣装置参数配置下的负荷损失量,为验证低压脱扣装置参数的改进措施提供支撑。
(2)仿真结果表明,通过求解低压脱扣装置参数优化配置模型得到的低压脱扣装置电压、延时整定值的设定方案,能够有效降低电压暂降下的负荷损失,验证了低压脱扣装置参数优化配置模型的合理性。
