基于超短时优化技术的轨交供电尖峰负荷平抑策略
2022-10-26赵文彬王小宇李诗晨
徐 斌,郑 欣,赵文彬,赵 健,王小宇,李诗晨
(1.上海电力大学电气工程学院,上海 200090;2.上海申通地铁集团有限公司,上海 201102)
1 引言
地铁供电网大都采用集中式供电方案,即每条地铁线路都是由专有的110 kV主变电所来供电,主变电所下设35 kV混合站来为地铁车站和列车供电[1,2]。集中式供电虽然便于对地铁供电网络进行统一管理,但由于全线的负荷都是由主所承担,故主变电所也承担着全线的尖峰负荷。
地铁尖峰负荷来源于列车的频繁启停,列车运行过程中的启动功率可达数兆瓦,每次启动都会产生一个冲击性负荷[3],由于集中式供电的原因,多辆列车启停的尖峰负荷会叠加到一起,形成较大的尖峰作用到主变压器低压侧。以上海地铁二号线为例,随着地铁客运需求逐步提升,列车行车间隔越来越小,实测尖峰负荷已达主变容量的40%~50%。相比于传统变压器,地铁主变负荷主要是尖峰负荷,虽然此时变压器的平均功率不高,但每一个尖峰负荷都近似于短时短路,较大的电流会导致绕组引线和接触点等部件的温度过高,影响变压器的使用寿命[4-6]。此外,尖峰负荷也会影响地铁供电网的可靠性,当尖峰负荷过大时,会导致线路短时过载,引起线路跳闸,严重时会损毁电力设备,降低了地铁供电网可靠性[7]。虽然列车行车间隔的减小有利于再生制动能量的回收,但此时尖峰负荷也会越来越大,随着未来地铁行车间隔的进一步减小,尖峰负荷将成为制约供电网可靠性提升的主要因素。
目前,国内外对于地铁供电网络尖峰负荷的研究较少。文献[8]分析了机车冲击性负荷对供电网电压波动的影响,仿真结果表明机车运行时会有冲击性的无功及有功产生,造成明显的电压波动,需要采取有效的手段对母线上电压波动进行控制。文献[9]研究了地铁冲击负荷对直流供网络继电保护的影响,对直流冲击特性与系统保护之间的配合关系提出了一些建议。文献[10]分析了列车冲击电流与短路电流的区别,通过频域特征提取方法区别短路电流,进而减小冲击性电流对继电保护的影响。文献[11]通过比例积分微分(Proportional-Integral-Derivative,PID)模糊控制列车电机端电压,在满足列车运行速度要求的前提下尽可能减小冲击负荷对电网冲击。文献[12]考虑了高速铁路牵引负荷不平衡性、冲击性和非线性特点,分析了牵引负荷特性对牵引变压器可靠性的影响。文献[13]针对冲击负荷对牵引变压器温度场和热老化特性进行了研究,研究了不同冲击条件下绕组温度场的分布特征,分析了冲击负荷的负荷率、冲击持续时间和冲击间隔时间对绕组热点温升的影响规律。
文献[8-13]分析了列车冲击性负荷对继电保护、电网电压波动、变压器寿命等造成的影响,并通过采取优化整定继保参数、调控电机运行策略等措施来降低冲击负荷造成的影响。
本文分析了地铁尖峰负荷形成的原理并提出了一种基于超短时优化技术的地铁尖峰负荷平抑策略。本文通过分析列车运行状态来建立单车冲击性负荷参数化模型,然后通过当前时间断面下全线各列车速度、位置和客流信息对各个列车的负荷进行预测,并结合供电网拓扑来预测未来一段时间域内地铁主变负荷,之后建立了以延时时间最小和能耗最小的多目标优化模型,并基于多目标优化模型和主变预测负荷,采用变步长优化对本时间域内各列车启动时间进行优化延时,由于优化延时时间很短,不会对后续运行列车产生影响,可以在不影响时刻表编排的情况下,最大程度减少主变尖峰负荷幅值,最后以某东部沿海城市地铁线路对本文提出的方法进行验证分析。
2 地铁主变电所尖峰负荷形成现象分析
地铁供电网负荷主要由动照负荷和牵引负荷组成。动照负荷占比约40%,主要是为地铁车站内照明、空调等供电,负荷全天变化不大,较为稳定[14];牵引负荷占比约60%,主要是为地铁列车供电。与动照负荷相比,牵引负荷的变化较剧烈,当列车启动时,列车会在短时间内加速到最大速度,此时牵引负荷会随列车加速起动而陡然增加,产生持续时间数十秒,高达数兆瓦的冲击性负荷。由于地铁车站站间距不大,普遍在2 km左右,因此列车起停较为频繁,当线路内的多个列车在较短时间间隔内相继启动时,多辆列车所产生的冲击负荷就会叠加形成尖峰负荷,此时主变压器会瞬间承受较大的尖峰负荷。
图1是某地铁110 kV主变电所牵引负荷曲线及其单个尖峰负荷分解图。可以看到牵引负荷是由无数尖峰负荷组成,每个尖峰负荷又由多辆列车的单车尖峰负荷叠加形成。受早晚高峰客流和行车密度的影响,尖峰负荷在早晚高峰时幅值较大。
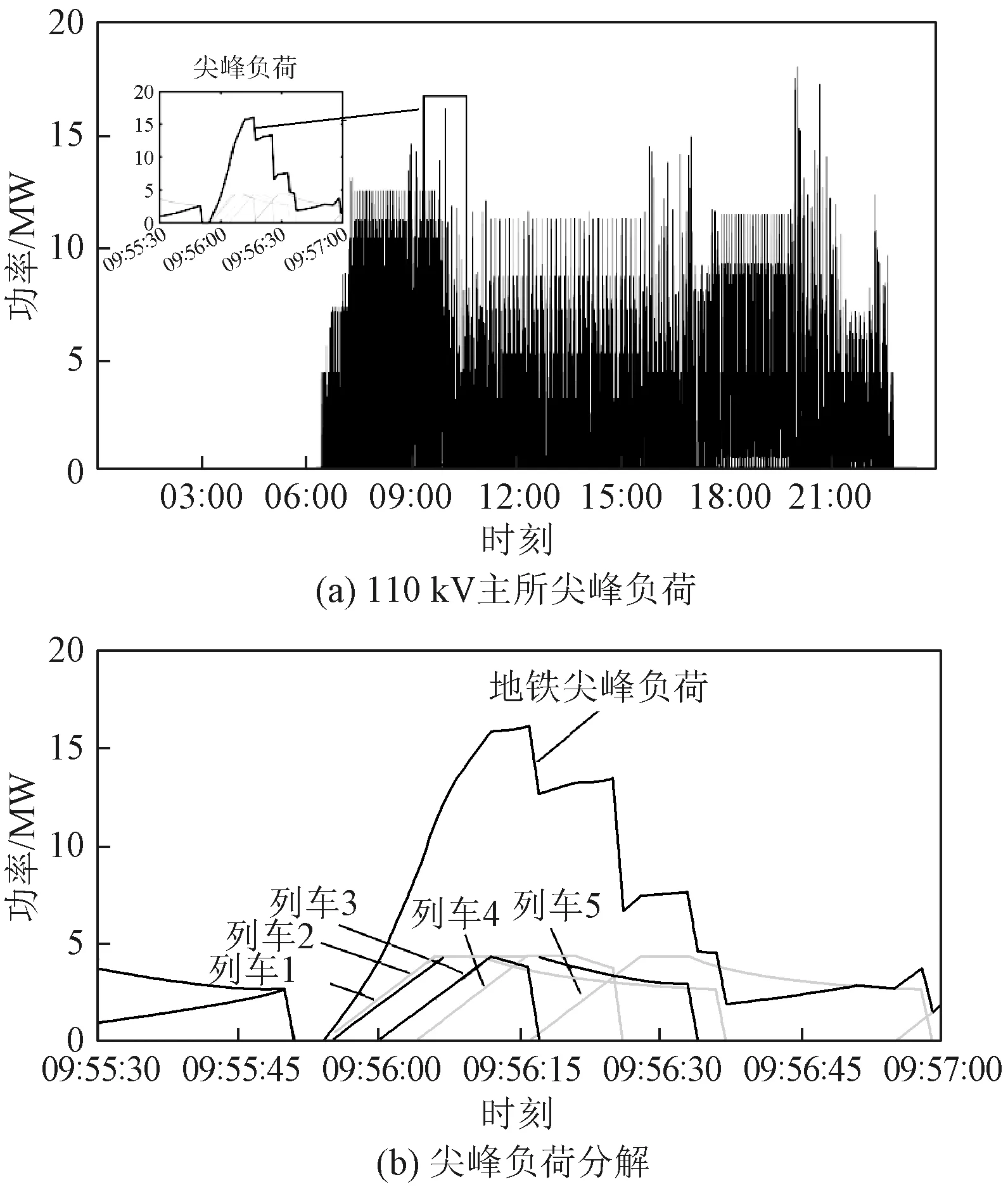
图1 地铁主变电所尖峰负荷的分解
列车冲击性负荷是由列车起停导致的。在列车的运行过程中会经历加速、惰行、制动三个阶段,但是列车只在加速过程中消耗电能,且加速过程较短,因此列车负荷会在较短的加速过程中达到峰值,随后列车进入惰行过程,列车在轨道内靠惯性滑行,不再消耗功率,列车负荷降为零。在列车制动过程中,制动能量会反馈到触网中,降低尖峰负荷的峰值。当多辆列车叠加到一起时,列车的再生制动反馈能量会抵消一部分的尖峰负荷[15]。
列车负荷与列车运行状态有关,由能量守恒可知,列车通过电机将电能转化为列车动能和热能,因此可以通过对列车运动状态的分析来建立不同参数下的各列车尖峰负荷模型。
3 单车短时冲击性负荷建模
3.1 列车运行状态分析
列车运行时会受到牵引力Ftra、基础阻力fb和附加阻力fa的联合作用。基础阻力由列车运行时的空气摩擦力、滚动摩擦力等组成,其大小与列车质量和运行速度有关,附加阻力是由于列车上下坡道受重力影响所产生。式(1)~式(3)为单列车运行过程中受力分析。
Ftra=aMty+fa+fb
(1)
fa=F(Mty,v)
(2)
fb=Mtygsinθ
(3)
式中,a为列车加速度;v为列车速度;g为重力加速度;θ为线路坡度;Mty为列车总质量;ty为列车状态,依据客流量的不同,地铁列车通常可以分为空载、轻载、满载和重载四种状态,分别对应着不同的列车质量。
通过列车速度与牵引力等运动状态信息可以计算列车机械功率,根据列车能量转化效率,进而求出列车电磁功率。式(5)、式(6)为单列车电磁功率计算公式。

(4)
Pm(t)=Ftra(t)v(t)
(5)
(6)
式中,v(t)为列车t时刻速度;Pm(t)、Pe(t)分别为列车机械功率和电磁功率;η为能量转化率。
3.2 列车各运行阶段的功率模型
列车运行过程可分为恒加速、恒功率、自然特性、惰性、制动五个阶段。在0~t1时,列车工作在恒加速阶段,此时列车加速度保持不变,约为1 m/s2;在t1~t2时,列车工作在恒功率阶段,恒功率过程中,列车输出功率保持不变;在t2~t3时,列车工作在自然特性阶段,自然特性过程中,功率与速度的乘积保持不变。式(7)~式(20)为单列车各运行阶段电磁功率计算公式。
(1)在列车恒加速过程中,a保持不变。
a1(t)=C1
(7)

(8)
(9)
式中,C1为列车起始加速度;a1(t)、v1(t)和Pe1(t)分别为列车在t时刻的加速度、速度和功率。
(2)在列车恒功率过程中,列车运行过程中的电功率Pe保持不变。
(10)
(11)
式中,C2为列车恒功率;v2、Pe2分别为列车在第二阶段的速度和功率。在自然特性过程中,功率与速度的乘积保持不变。
C3=Ftra(v2)2
(12)
(13)
(14)
式中,C3为功率与速度的乘积;v3、Pe3分别为列车在第三阶段的速度和功率。
(3)惰行过程,列车依靠自身惯性滑行。列车惰性过程初始时速度达到最大值,列车没有功率输入,依靠自身惯性滑行,此时列车仅受阻力作用。
(15)
Pe4=0
(16)
式中,v4、Pe4分别为列车在惰性过程的速度和功率。
(4)制动过程,在t4~t5时,列车进入制动过程。列车制动采用再生反馈制动,此时电动机运行在发电机状态下,产生的功率倒送回触网,供给其他列车用电[16],当电网电压升高到DC1 800 V时接入稳压电阻,将列车动能转化为热量,当列车速度下降到5 km/h时采用机械制动,不再有功率反馈。
a5=C4
(17)

(18)
(19)
(20)
式中,C4为列车制动加速度;a5、v5和Pe5分别为列车在第五阶段的加速度、速度和功率。
列车负荷不仅包括牵引负荷还有列车内空调、照明系统等基础负荷,因此列车运行过程总负荷Ptra应等于Pe与列车基荷Pb之和。列车基础负荷占比较小且不随运行状态变化,因此本文用常量表示。单列车牵引功率计算如下式所示:
Ptra=Pe+Pb
(21)
4 地铁主变尖峰负荷建模
4.1 基于运行状态的列车冲击性负荷预测
地铁列车大都是主控系统根据运行图进行自动控制,但是由于列车运行过程中会受到列车车门不能及时关闭、列车运行速度偏差和运维人员调度等外界因素的影响,导致列车不能完全按照时刻表运行,因此本文根据各个列车的运行速度、位置和客流信息来预测当前列车的负荷。
由于各供电区间长度不变,因此可以根据列车运行里程来判断当前列车驶入了哪个供电区段。地铁供电区段判断条件如下式所示。
(22)
式中,I为供电区段;xtr为第tr辆车的里程;Di为第i个供电区段的长度。
将列车的速度或位置代入冲击负荷模型Θ中都可获取当前列车的负荷,为了减小干扰误差,取根据速度或位置识别出的负荷均值作为列车在时刻t的负荷。
将列车位置xtr和供电区段I代入单车冲击负荷模型中,得到根据列车位置计算的第tr辆列车的负荷Ptr_x如下式所示:
Ptr-x=Θ(xtr,I)
(23)
由于列车在加速和减速过程中都会经过相同的速度,但在加速时列车吸收功率,功率为正,减速时,列车反馈功率,功率为负,因此先采用列车位置来判断当前处于加速过程还是减速过程,然后再根据速度对列车负荷进行识别。列车负荷识别如下:
(24)
(25)
式中,Ptr_v为根据列车速度来识别的列车负荷;xi(t)为列车在t时刻的位置;Ptr为列车在t时刻的最佳模型识别负荷。
4.2 主变尖峰负荷预测模型
得到各列车负荷之后根据地铁供电网拓扑,计算主变侧负荷。地铁供电网络通常会沿着地铁线路设置数十个35 kV变电所,这些变电所负责给列车和车站供电,其中为列车供电的称为牵引站,为车站供电的称为降压站,混合站既可以为车站供电,也可以为列车供电。图2是地铁直流牵引系统的示意图,地铁直流牵引系统主要由牵引变、整流器、接触网、钢轨和回流线组成。不同于高铁,地铁车站之间距离较短,压降较小,地铁牵引系统采用DC750 V~DC1 800 V直流电为列车供电。直流供电系统采用接触网或第三轨供电,接触网或第三轨供电为正极,钢轨与回流线接负极[17]。列车在某一供电区间运行时由供电臂两端的牵引变电所供电,即双边供电[18]。
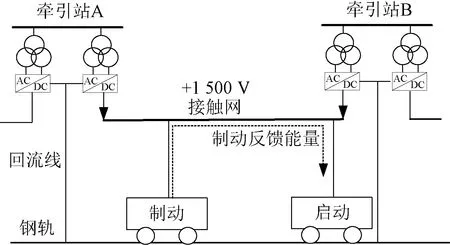
图2 地铁直流牵引系统组成
当地铁直流牵引系统安装再生反馈装置时,列车制动功率可以反馈回35 kV电站;没有安装再生反馈装置时,若同一供电区间内的负荷出现负值,则认为此时列车采取电阻制动,舍弃负值,式(26)~式(28)为地铁牵引变功率计算公式。
Pint=∑Ptr
(26)
若Pint<0Pint=0
(27)
式中,Pint为供电区段内总牵引负荷。
第三轨的电阻约为0.02 Ω/km,地铁的供电区间一般为2 km,线路电阻较小,故本文不再考虑供电线路上的压降。
(28)
式中,Psta为地铁牵引变功率。
降压变电所为车站内照明、空调等供电,这部分负荷称为动照负荷,动照负荷变化较为缓慢,与地铁尖峰负荷相比,动照负荷在分钟尺度内变化不大,本文取动照负荷为恒功率负荷。
地铁35 kV变电站之间一般采用双环网接线,每个车站采用单母线分段,母联断路器常开,车站之间手拉手形成双环网接线[19-21]。图3为地铁中压供电网电气主接线图,上级主变电所母线WA1和WA2分别为下级35 kV变电所母线W21、W31和W22、W32供电。

图3 地铁中压供电网电气主接线
本文采用只有0和1的矩阵对供电网进行建模,定义矩阵Madj为:
Madj=[as,t]
(29)
式中,Madj为s行t列的矩阵;as,t为0、1变量,当出线s给母线t供电时,as,t为1,否则为0。
MstaP=[Psta]
(30)
Msub=MadjMstaP
(31)
Psub=sum(Msub)
(32)
式中,MstaP为35 kV变电所负荷矩阵;Msub为主变出线负荷矩阵;Psub为主变电所总负荷。
5 基于超短时错峰优化的主站尖峰负荷优化模型
主站侧的尖峰负荷是由多辆列车在较短时间内相继起动造成的,因此本文通过将造成尖峰负荷的列车起动时刻错开Δt来降低尖峰峰值。图4是地铁列车起停运行图,列车起动时间是t0,到站时间是t2。在实际运行中,为留有一定的安全裕度,列车通常会早于规定的到站时间t2,在t1时刻提前到站,此时就会留有一个时间裕度Δtmax,因此通过造成主变尖峰负荷过大的多辆列车依次延时起动的方法既可以优化尖峰负荷,也不会影响列车正常的运行[22]。
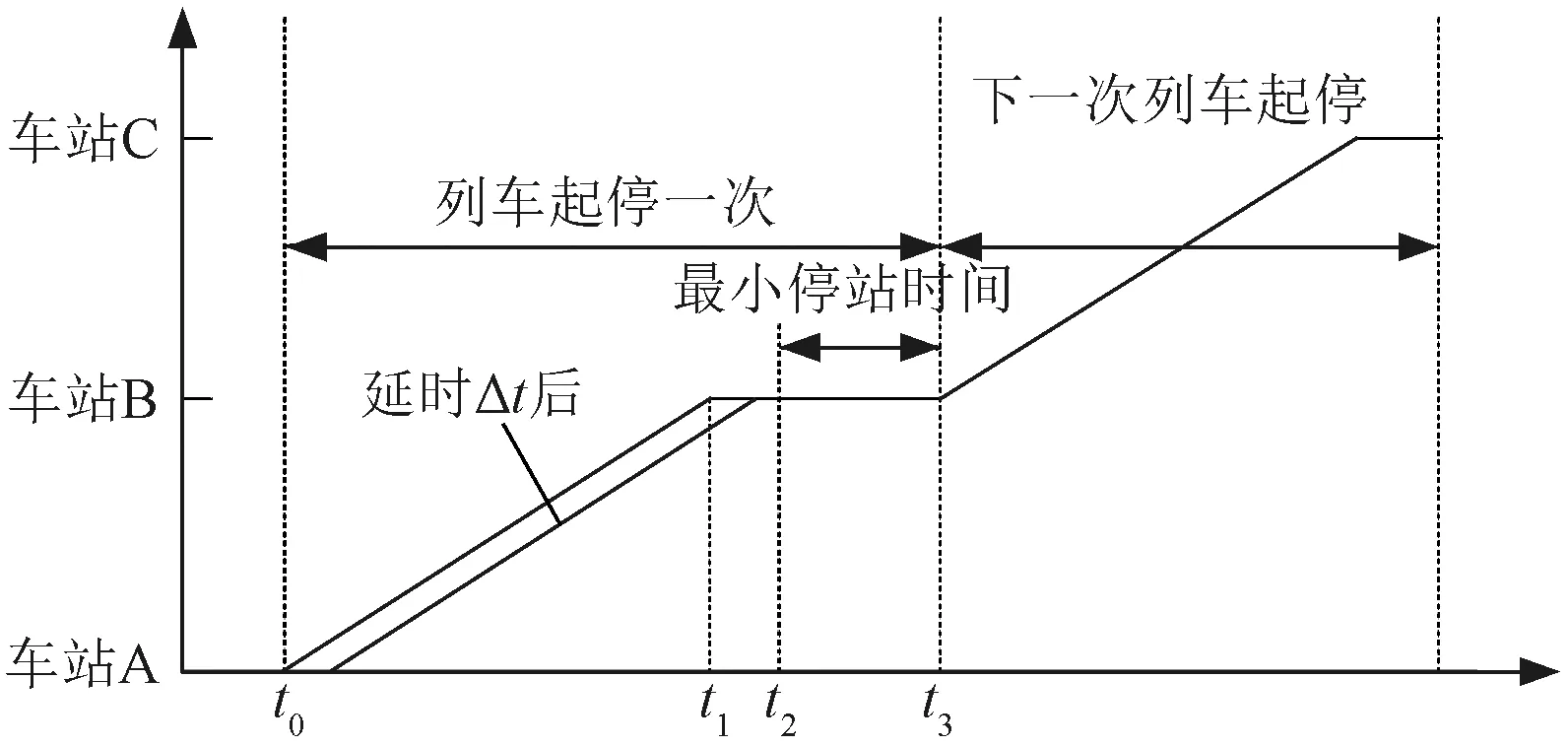
图4 地铁列车起停运行图
Δtmax=t2-t1
(33)
本文采取滚动优化的方法,以m为优化步长,建立单个时间域内主站负荷模型,分时间域进行优化。在时间域Θ(t,t+m)内,通过建立目标函数寻优求解。若时间域内依次有t1,t2,…,tk共k个列车起动时刻,其修正量分别为Δt1,Δt2,…,Δtk,建立目标函数如下式所示:
(34)
式中,k1和k2为权重系数,添加主变尖峰负荷峰值约束和延时时间约束;PT_t为主变压器在t时刻下的功率。
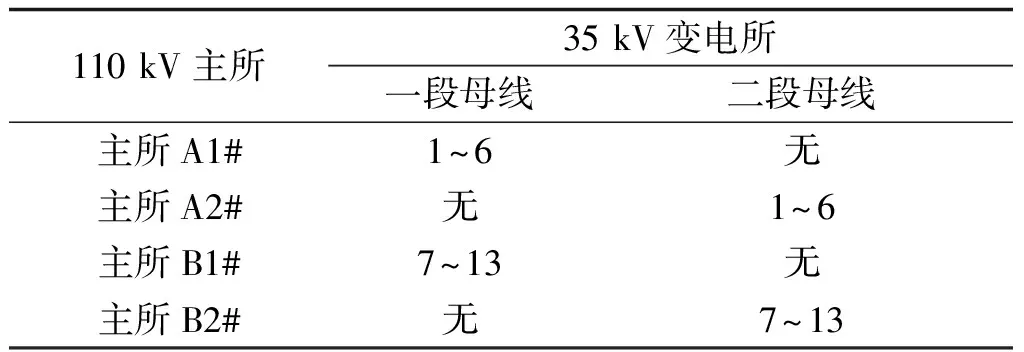
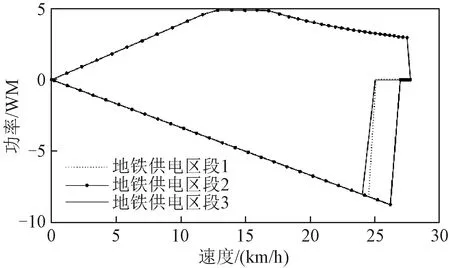
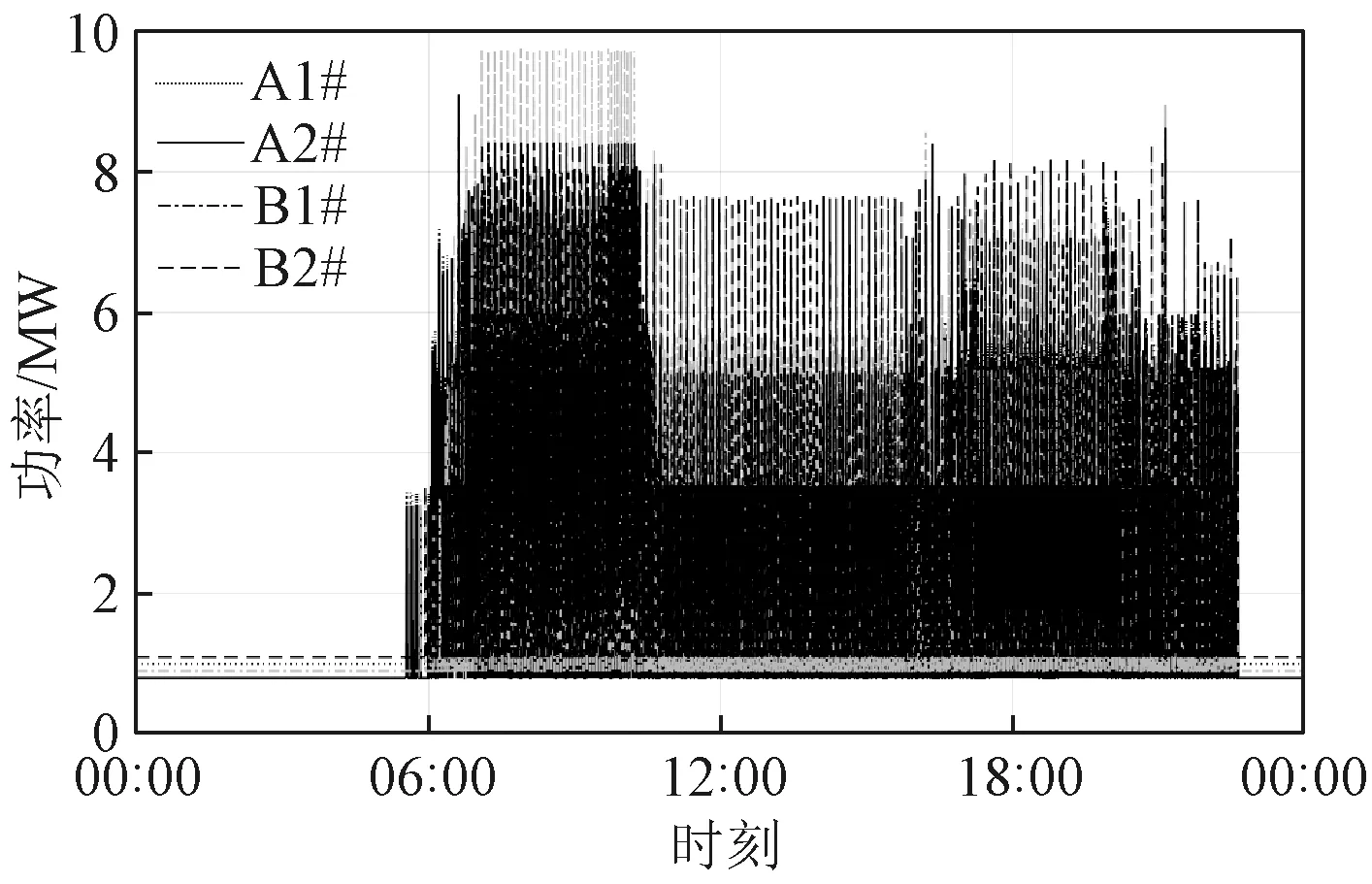
maxPT (35) Δti<Δtmax∀i (36) 式中,PT为主变压器功率;PT_max为主变压器功率峰值;Δtmax为最大修正时间裕度。 图5为本次主变尖峰负荷滚动优化流程图,主变电所尖峰负荷滚动优化流程如下所示: 图5 主变尖峰负荷滚动优化流程图 步骤1:建立单车负荷模型,获取列车速度、位置与功率之间的关系,初始化优化步长m和列车起动时刻序列T。 步骤2:通过t时刻列车的运动状态Si(v,x),代入主站负荷模型计算时间域Φ(t,t+m)内的主变功率PT。 步骤3:代入尖峰优化模型,求解当前时间域Φ内起动时刻序列修正量ΔT。如果有解则将列车起动时刻序列T更新为T+ΔT,执行本时间域内的优化,更新t=t+m,执行步骤1。 步骤4:如果无解将m更新为m+1,重新执行步骤3。当m大于其阈值时则放弃本时间域优化,直接执行步骤1,实现动态优化。 为了验证本方法可行性,本文采用某东部沿海城市地铁线路为例进行验证分析。该线路共有16辆6A型列车,全天共运行340列次,其中,上行170列次,下行170列次。取客流量为满载情况下,列车总重量为333.45 t。全线共有2所110 kV主变电所,13所35 kV混合所,每个110 kV主所设有两台10 MV·A的变压器。全线共设13个车站,采用12个供电区间,每个车站分别由一所35 kV混合所供电。各车站动照负荷见表1,其中车站1由其他主所供电,故为0,车站8~10处于商业区,动照负荷较大。 表1 地铁车站动照负荷 每个车站分别由35 kV混合所供电,每个混合所均采用单母分段接线,混合所之间采用手拉手接线方式。各个混合所都是由2个110 kV主所供电,其供电范围见表2,主所A为1~6号变电所供电,主所B为7~13号变电所供电。 表2 主变电所供电范围 将列车质量与牵引力等原始数据信息代入单车负荷模型,取客流量为满载时,建立各个供电区段的单车冲击负荷模型。对于各供电区段负荷,也通过安装负荷监测装置,通过对负荷的实时监听来获得。 图6为1~3号供电区段的负荷模型,各区段加速阶段相同,负荷最大为5 MW。减速阶段略有不同,2号供电区段再生制动反馈最大,达到9 MW。 图6 1~3供电区段负荷模型 建立单车尖峰负荷模型库之后,根据列车运行图预测各个供电区间未来的负荷曲线,并根据预测结果计算主变尖峰负荷。图7为未优化前110 kV主变一天的尖峰负荷曲线。列车全天耗能约220.87 MW·h,尖峰负荷最高峰值约为9.8 MW。 图7 110 kV主变侧尖峰负荷 考虑到实际应用情况,取最大修正时间裕度为40 s,每5 s为一个优化阶梯,分别计算Pmax为变压器容量90%,80%,70%和60%下的优化错峰方案。 (1)场景一:90%SN,Pmax=9 MW 图8为场景一下主变负荷与车次延时优化结果图,优化后全天共需延时29车次,共延时290 s,全天共耗电220.61 MW·h,相比原来未优化时每天节省电能约260 kW·h。 图8 场景一下的主变负荷与车次延时 (2)场景二:80%SN,Pmax=8 MW 图9为场景二下主变负荷与车次延时优化结果图,优化后全天共需延时128车次,共延时1 290 s,全天共耗电220.60 MW·h,相比原来未优化时每天节省电能约270 kW·h。 图9 场景二下的主变负荷与车次延时 (3)场景三:70%SN,Pmax=7 MW 图10为场景三下的主变负荷与车次延时优化结果图,优化后全天共需延时617车次,共延时7 980 s,全天共耗电219.96 MW·h,相比原来未优化时每天节省电能约910 kW·h。 图10 场景三下的主变负荷与车次延时 (4)场景四:60%SN,Pmax=6 MW 图11为场景四下的主变负荷与车次延时优化结果图,优化后全天共需延时996车次,共延时16 380 s,全天共耗电219.43 MW·h,相比原来未优化时每天节省电能约1 440 kW·h。 图11 场景四下的主变负荷与车次延时 各场景下优化结果见表3,随着Pmax减小,节约的电能上升,但列车的延时时长也随之增加,分析不同优化目标下的优化结果,总延时时长与Pmax之间并非是线性关系,将Pmax与延时车次做回归分析,如图12所示。 表3 各场景下优化结果 图12 延时车次与尖峰负荷幅值 最大尖峰负荷与Pmax与延时车次近似为对数模型关系,根据各场景计算结果,取Pmax为9 MW或8 MW时,可以取得综合最优结果。 为了应对各种不确定因素对列车运行造成的影响,列车时刻表在编排时通常会预留出一定的时间裕度,这就为在不更改时刻表的前提下对地铁列车牵引负荷进行短时错峰优化提供了可能。本文首先根据对单车平直道运行状态进行分析建立了各个供电区间单车功率模型,然后采集当前时间断面下在线各列车运行的速度和位置信息,将所采集到的信息代入各个供电区间段功率模型当中,预测下一个时间域内各供电区段负荷,之后通过建立以最小延时时间和最小能耗为目标的多目标函数来对当前时间域内要起动列车的起动时刻进行短时延时,如果无解则扩大时间裕度进行求解,通过自适应时间域来尽可能减少不确定因素对预测模型造成的影响,最后以某地铁线路对本文提出的方法进行验证分析,仿真结果表明: (1)通过对地铁线路各列车起动时刻进行短延时优化可以在不改变列车运行时刻表的前提下有效地减少地铁主变电所尖峰负荷幅值。 (2)列车起动短延时错峰不仅可以降低主变电所尖峰负荷峰值,而且可以增加再生制动反馈能源利用率,且尖峰负荷峰值越低,再生制动反馈能源利用率越高。 (3)延时车次与尖峰峰值的关系为对数模型关系,即每削减单位尖峰负荷所需延时车次呈指数增加,需要根据不同时刻表综合考虑各方面成本来制定Pmax。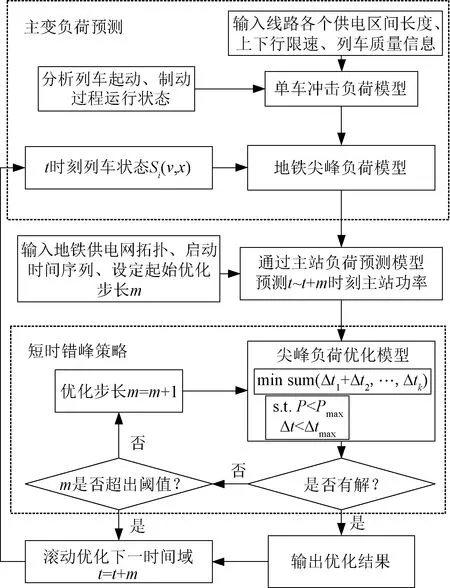
6 算例分析
6.1 算例原始数据

6.2 原始主站负荷建模分析
6.3 不同目标下短时错峰方案






7 结论
