利用导数研究复杂不等式问题的方法探究

李 虎

(广东省中山市第一中学)

本文收集了一学年以来,在历次考试和作业中,学生出现问题较严重或反复问的重难点问题,主要以导数研究复杂的不等式问题为契机展开,分享给将要学习这一块或高三复习这一块内容的学生.这一块内容一直是学生比较害怕的,得分率也比较低,但从最近几年的高考看,这块内容的分值占比还比较大,因而需要学生在复习备考中,沉下心来,多梳理总结,发现规律.

1 方法探究

1.1 隐零点法

当导函数的零点无法求解时,可以借助单调性和零点存在性定理确定零点的大致范围,此时需要注意导函数等于零这一条件的应用,因为它往往起到化简的作用.

1.2 切线放缩法

切线放缩法即对于一个函数来说,取其某点的切线,如果函数图像在切线的一侧,则可以得到一个不等式,这个不等式即为切线放缩不等式.

1.3 凹凸反转

凹凸反转法是指一个函数如果本身没有最小值(或最大值),但是除以一个比自己增长速度慢(或速度快)的函数后有最小值(或最大值),则其具有凹凸性,常用它证明不等式.

例3已知函数f(x)＝axeax＋(a＋b)x,g(x)＝(1＋x)lnx.

(1)当a＝－b＝1时,证明:f(x)＞g(x)在(0,＋∞)上恒成立;

(2)若∀x∈(0,＋∞),都∃b∈[－1,0],使f(x)≥g(x)恒成立,求实数a的取值范围.

证明(1)证法1(切线放缩法) 由于ex＞x＋1,故在x＞0上,xex＞x(x＋1)＞(x＋1)lnx.

1.4 同构式

同构式法是指将结构相同的代数式分离出来,再构造函数利用函数的单调性进行研究.这里经常用到如下两个恒等式:

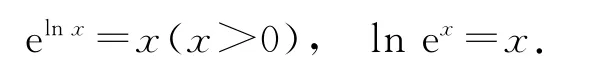
下面用同构式法求解例3的第(2)问.

解析因为∃b∈[－1,0],使f(x)≥g(x)恒成立,令φ(b)＝axeax＋(a＋b)x,则只需要φ(b)max≥g(x),即axeax＋ax≥(1＋x)lnx在x∈(0,＋∞)上恒成立,整理得

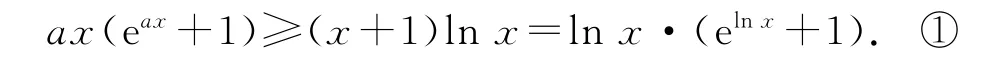
设F(x)＝x(ex＋1),则F′(x)＝ex(x＋1)＋1,又F″(x)＝ex(x＋2),所以当x＞－2时,F″(x)＞0,F′(x)单调递增;当x＜－2时,F″(x)＜0,F′(x)单调递减,故当x＝－2时,F′(x)有最小值F′(－2)＝,所以F(x)在R 上单调递增,式①即F(ax)≥F(lnx),所以ax≥lnx,即

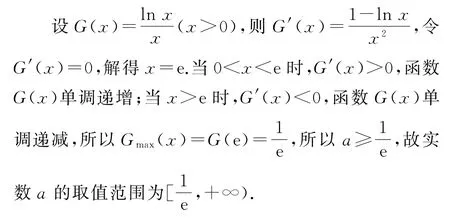
1.5 构造辅助函数

构造辅助函数的关键是将各个值中共同的量用变量替换,再利用函数的单调性比较大小.

例4(2021年全国乙卷理12)设a＝2ln1.01,b＝ln1.02,c＝－1,则( ).

A.a＜b＜cB.b＜c＜a

C.b＜a＜cD.c＜a＜b

综上,b＜c＜a,故选B.

1.6 定义域分段研究

如果导数题目中含有三角函数,因三角函数本身固有的周期性、有界性、单调性,故需对函数的定义域进行分段研究,更好地利用三角函数的性质.

例5已知函数f(x)＝ex＋cosx－2,f′(x)为f(x)的导函数.

(1)当x≥0时,求f′(x)的最小值;

(2)当x≥－时,xex＋xcosx－ax2－2x≥0恒成立,求a的取值范围.

解析(1)由题得f′(x)＝ex－sinx,f″(x)＝excosx.当x∈[0,π)时,f″(x)为增函数,且f″(x)≥f″(0)＝0;当x∈[π,＋∞)时,f″(x)≥eπ＋1＞0.故当x≥0时,f″(x)≥0,故f′(x)为[0,＋∞)的增函数,即f′(x)的最小值为f′(0)＝1－0＝1.

若a＞1,则由(1)知,h′(x)＝ex－sinx－a在[0,＋∞)上单调递增,且

h′(0)＝1－a＜0,h′(1＋a)≥e1＋a－1－a＞0,故存在唯一x2∈(0,＋∞),使h(x2)＝0,当x∈(0,x2)时,h(x)单调递减,h(x)＜h(0)＝0,此时xh(x)＜0,矛盾.

综上,a≤1.

1.7 变方程为不等式

有些方程的根无法解出时,可以借助代换法,将其整体代换,再结合不等式求其值.

2 小结

导数只是研究函数的一个工具,其主要作用是将研究函数的单调性、极值、最值问题转化为研究导函数的符号.不等式问题有时会与最值、极值问题综合考查.这两年的考题有涉及二阶导函数甚至三阶导函数,需要学生梳理导数的知识脉络.条理清晰是解答导数题目的关键,学生平时要多总结一些解题技巧和方法,尤其是熟悉新教材的例题和课后题的结论.

(完)