掌握通性通法,以不变应万变——基本不等式的应用技巧

徐志莲

(浙江省桐庐中学)

基本不等式及其应用作为高考中的一个重要知识点,一直是高考命题的一个热点与亮点.利用基本不等式解决问题时,需要把握问题本质,掌握基本的通性通法,举一反三,融会贯通,发散拓展,才能以不变应万变.

不等式能与其他知识进行合理巧妙的交会与融合,可以有效考查学生的数学抽象、逻辑推理和数学运算等核心素养.利用基本不等式解决最值问题时,要同时具备“一正、二定、三相等”这三个基本条件,而在具体问题中,这三个基本条件不直观、不直接,需要进行适当的变形才能得以满足.解决问题的基本技巧就是创造条件,合理变形,借助基本技巧与方法来化归与转化,实现利用基本不等式解决问题的目的.

1 双变量首选——消元法

例1已知正数x,y满足x＋4y＝x2y3,则的最小值为_________.

分析根据题目条件直观分析,本题不满足利用基本不等式来求解最值的条件——“积为定值”,并且题目条件的关系式与目标代数式之间的关系不清晰,所以考虑通过消元法处理,减少变量,使得关系更加清晰明了,进而通过等式的恒等变形与转化,结合基本不等式来确定相应的最值问题.

解由正数x,y满足x＋4y＝x2y3,整理可得y3x2－x－4y＝0,根据求根公式解关于x的一元二次方程,可得x＝(负值舍去),根据基本不等式,通过消元法处理,可得

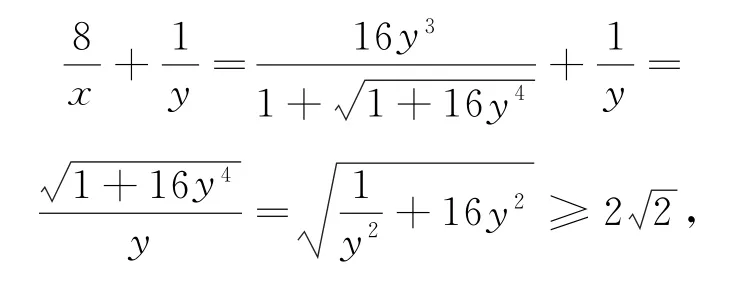
点评在解决一些比较复杂的多变元代数式最值问题时,通常利用变量之间的关系进行合理的消元处理,通过减少变量的个数,将所求问题转化为只含一个变量的代数式问题,再借助单变量代数式的变形与转化,更加直观有效地利用基本不等式进行求解.

2 乘“1”后变形——代换法

例2已知a＞0,b＞0,且2a＋＝1,则＋b的最小值为( ).

分析根据题目条件,观察条件代数关系式与目标代数关系式之间的联系,在所求目标代数关系式后面乘以“1”后,借助已知条件中的关系式来代换常数“1”,构造对应的代数式,通过代数式的展开处理并加以恒等变形与转化,进而利用基本不等式来确定代数式的最值.

点评“1”的代换法是拼凑成满足基本不等式条件的关键所在,也是利用基本不等式求最值中比较常用的方法之一.

3 常量巧引进——配凑法

例3若a＞0,b＞0,且a2＋＝1,则的最大值为_________.

分析本题要求代数式的积的最大值,但不具备“和为定值”的基本条件,无法直接利用基本不等式求解.结合条件中的二次关系式,对目标代数式进行变形,构建满足对应二次方程的条件,提供“和为定值”的情境,为利用基本不等式求解最值进行基本的铺垫工作.

点评在利用基本不等式确定目标关系式的最值时,为创设满足“积为定值”或“和为定值”这一基本条件,经常需要对关系式进行因式分解、平方转化等恒等变形,即根据条件所给代数式和待求目标代数式的结构特征,引入常量进行必要的配凑处理,构建满足应用基本不等式的条件.

4 整体性思维——换元法

例4已知实数a,b满足a＞b≥0,则的最小值是_________.

分析根据题目条件,利用不等式的性质确定对应的关系式恒为正数,且目标代数式的分母不是单项式,因而考虑对目标代数式进行恒等变形与转化,再通过换元法处理,这样可以使得相应的目标代数式更加简洁直观,为进一步利用基本不等式确定最值问题指明方向.

解由于实数a,b满足a＞b≥0,则知a＋b＞0,a－b＞0,设a＋b＝x＞0,a－b＝y,则a＝,b＝.

由基本不等式可得

点评求解本题的关键是根据题目中目标代数式的结构特征对分母换元.特别地,换元后的恒等变形往往是解决此类多元(一般以二元或三元为主)函数或代数式的最值或取值范围问题的关键步骤.

利用基本不等式解决代数式的最值问题,关键在于掌握基本的通性通法,合理借助“拆”“拼”“凑”等技巧,将题目条件中的代数式或所求的目标代数式变形为“和为定值”或“积为定值”的形式.但是具体问题千变万化,解法千奇百怪,方法还不具有唯一性,因而需要学生尽可能地掌握解决问题的通性通法.

链接练习

1.正实数a,b,c互不相等且满足a2＋b2＋c2＝2ab＋bc,则下列结论成立的是( ).

A.2a＞b＞cB.2a＞c＞b

C.2c＞a＞bD.2c＞b＞a

链接练习参考答案

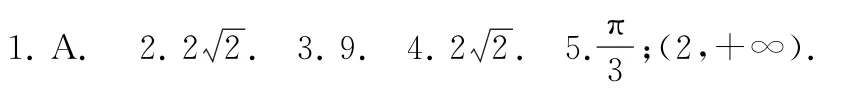
(完)