探求多元等式条件下最值问题的若干策略

李学友 刘 芳

(湖北省荆门市第一中学)

用基本不等式解决某些含有多元等式条件的最大值或最小值问题是一种常见的策略,但有些题目的条件隐、式子晦.结构复杂,需要有扎实的基本功和一定的解题技巧.这些能力的来源是接受规范的解题方法指导和一定量的典型题目训练.本文通过具体例题介绍一些常用的解题方法,以期给读者一些帮助.

1 等式变形

点评在研究题目后发现,结论式子中的分母分别是a和b＋1,如何利用好等式条件将分母进行转化是解题的关键,由a＋b＝1 变形得a＋(b＋1)＝2就是一个解题的技巧.所以最小值为25.

点评本解法瞄准待求的结论,先对给出的条件变形,然后再依据条件式的特点,对待求式进行多轮的变形转化,达到解题目的.

2 三角换元

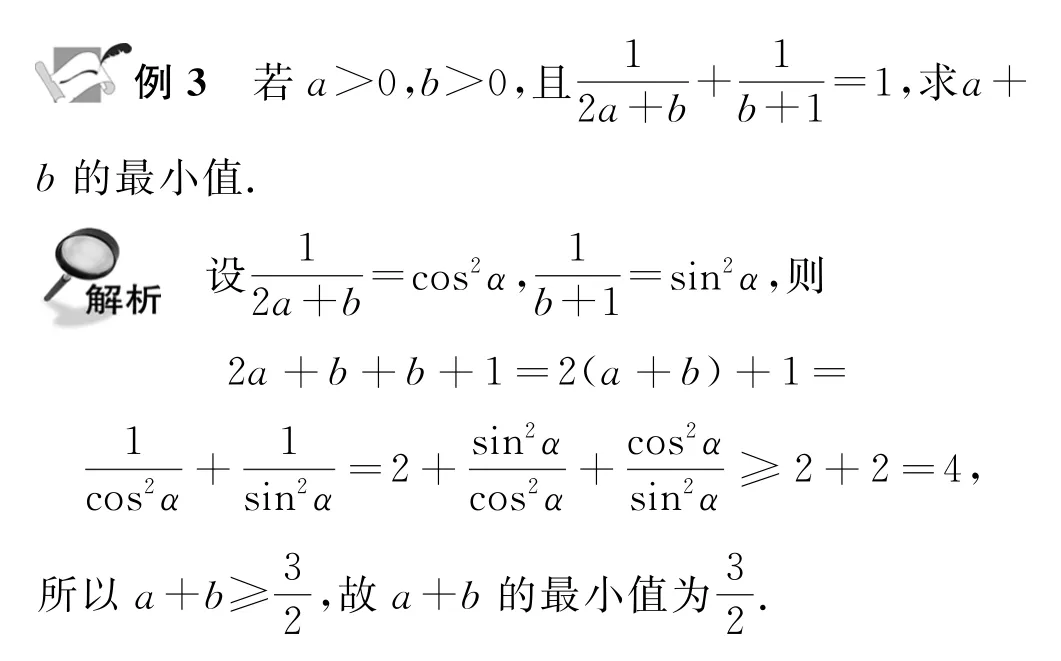
点评如果条件中含有两个正项和为1(或某个特定的值),这就是选用三角换元的重要信号,通过换元变形,就可以利用三角函数的相关知识求解.

3 多次放缩

点评本题的待求式结构比较复杂,解题过程中两次运用了基本不等式进行放缩,由于连续放缩时,取等号的条件一致或互相之间没有影响,故而是完全可行的.

点评本题在将已知条件有效代入并化简变形后,出现了使用基本不等式解题的契机,但有关项不是正数,需要利用绝对值放缩,注意此处的放缩不影响后面基本不等式的使用条件.

4 替换转化

当且仅当x＋s＝3时,待求式取得最小值6.

点评本解法通过对所给等式和结论式进行转化和替换后,为利用基本不等式解题创造了条件,化解了问题难点.如果没有抓住x＋s＞0的特点,把x＋t当成变元,可能造成解题混乱.

点评本解法通过挖掘已知条件,抓住条件式与待求式的关系,构造出可用基本不等式求解的表达式,化解了问题的难点.

5 精准换元

点评通过将欲求的表达式换元后代入已知等式,得到了一个关于x的一元二次方程,然后利用方程有实数解的原理,根据根的判别式列出不等式,通过解此不等式得出答案.

通过对几个典型题目的分析,列举了常用的解题方法,可以看到,基本不等式是解决含有多元等式条件的最大值或最小值问题的重要方法,当然还需要许多其他方法进行配合.需要注意的是,含有条件等式问题只是诸多利用基本不等式求最值中的重要一类,还有其他多种题型,限于篇幅,在此不再赘述.

(完)