初中数学有效复习“精讲精练”教学法——以“二次函数与反比例函数”为例

⦿安徽省蒙城县庄子中学 杜 宇

1 引言

复习课是为了让学生回顾、巩固、消化、归纳数学基础知识，提高分析、解决问题的能力.一堂有效的数学复习课，不仅能够让学生巩固知识、查漏补缺，而且要温故知新.

初中数学复习“量大、面广、知识点多、时间紧”，要让学生在短时间内系统有效地复习，“精讲精练”不失为一种行之有效的方法.教师要认真筛选和精心设计一定量的具有“概念性、典型性、针对性、综合性、启发性、思考性、灵活性、创造性”等特点的例题、习题，通过“精讲精练”来达到巩固与提高的目的[1].

“二次函数与反比例函数”，是沪科版九年级上册第21章的内容.本章共有6节，复习的量大、面宽、时间紧，不可能做到面面俱到，只能“突出重点、化解难点、以点带面”.因此，本章复习的重难点是：熟练掌握和运用二次函数、反比例函数的图象和性质，培养在解决实际问题时建立函数模型的意识，并能掌握建立函数模型的技能.精选适量的典型例题，精讲、分析解决这些问题，做到以点带面，是本章复习教学的主要方法[2].下面通过典型例题来了解和掌握“精讲精练”复习法.

2 “精讲精练”复习教学法的运用

2.1 “小题大做”收奇效

适当变化的小题可以涵盖丰富的基本知识、基本技能，进一步突出转化、建模、运动、分类讨论等思想的培养，使学生能够从数学的角度思考问题，用比较规范的逻辑推理形式表达自己的演绎推理过程.在复习课上尝试“小题大做”，那些精练的小题往往能够收到意想不到的效果.

例1已知x=5时，y=x2+px+q的最小值为-2，则p=______,q=______.

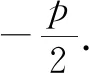
2.2 归类训练找方法

归类训练就是把类型相同或相似的题型放在一起，只要讲(练)一个或几个题目，就可以找到并掌握解决这类问题的方法与技巧，避免陷入题海而不能自拔，达到触类旁通、以点带面、举一反三的效果.

(1)试写出年利润S(单位：万元)与广告费x的函数关系式，并计算广告费是多少万元时，公司获得的年利润最大，最大年利润是多少万元？

(2)把(1)中的最大利润留出3万元做广告，其余的资金投资新项目.现有6个项目可供选择，各项目每股投资金额和预计年收益如表1.

表1 各项目每股投资金额与预期收益

如果每个项目只能投一股，且要求所有投资项目的收益总额不得低于1.6万元，那么有几种符合要求的投资方式？写出每种投资方式所选的项目.

当x=3时，年利润S取得最大值16.

所以，当广告费是3万元时，公司获得的最大年利润是16万元.

(2)用于再投资的资金是16-3=13(万元)，经分析，有两种投资方式符合要求：

一种是取A，B，E各一股，投入资金为5+2+6=13(万元)，收益为0.55+0.4+0.9=1.85(万元)>1.6(万元)；另一种是取B，D，E各一股，投入资金为2+4+6=12(万元)<13(万元)，收益为0.4+0.5+0.9=1.8(万元)>1.6(万元).

点评:本题属于“获取最大利润”类习题，实际上就是求二次函数的最大值或最小值.解这类题型首先要明确利润=(销售单价-每件成本)×销售量；然后求出函数表达式和自变量的取值范围，再通过配方变形，或利用公式求出最大值或最小值.要注意的是，由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内，若忽视了自变量的取值范围往往会造成解题错误.

2.3 一题多解拓思路

通过对典型例题解法的讲练与拓展，有针对性地引导学生进行一题多解训练，以拓宽学生的解题思路，不断提高学生灵活运用各种知识的综合能力.

所以,抛物线的解析式为y=x2+4x+2.

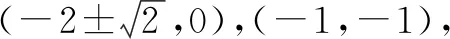
所以,所求解析式为y=x2+4x+2.

3 结论

教学实践表明，初中数学复习课中，采用“精讲精练”法，以例题为中心，通过小题大做、归类训练、一题多解等方式来组织教学，将某一章节内容的基本知识串起来讲练，既能巩固加深已学过的旧知识，又能够让学生熟练掌握多种题型的解题方法与技巧[3].