Observation of quadratic magnetoresistance in twisted double bilayer graphene

Yanbang Chu(褚衍邦) Le Liu(刘乐) Yiru Ji(季怡汝) Jinpeng Tian(田金朋)Fanfan Wu(吴帆帆) Jian Tang(汤建) Yalong Yuan(袁亚龙) Yanchong Zhao(赵岩翀)Xiaozhou Zan(昝晓州) Rong Yang(杨蓉) Kenji Watanabe Takashi TaniguchiDongxia Shi(时东霞) Wei Yang(杨威) and Guangyu Zhang(张广宇)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

4Research Center for Functional Materials,National Institute for Materials Science,1-1 Namiki,Tsukuba 305-0044,Japan

5International Center for Materials Nanoarchitectonics,National Institute for Materials Science,1-1 Namiki,Tsukuba 305-0044,Japan

Keywords: twisted double bilayer graphene,Kohler’s rule,magnetoresistance scaling,critical behavior

Magnetoresistance (MR) is a measure of resistance to the change of magnetic field, and it provides rich information about Fermi surface,carrier scatterings,and exotic phases for a given electronic system.[1–4]MR is quantified as MR=[Rxx(B)-R0]/R0, whereR0is the resistance at zero magnetic field. From Drude formula, the MR in metals is usually quadratic in magnetic fieldB. More generally, it follows the Kohler’s rule.[1,3,5]that MR in metals scales as a function of the ratioB/R0, i.e., MR =f(B/R0). Kohler’s rule has been found to be valid in various materials including metals,semimetals,and cuprate superconductors.[6–11]Meanwhile,the violation of Kohler’s rule has also been widely observed and often related to Fermi surface reconstruction,magnetic breakdown, anisotropic effects, quantum correction to resistance, and other carrier scattering mechanisms (phonon scattering or electron–electron interaction),[1,3,12–16]reflecting emergent physics. One example is the strange metal phase observed in iron pnictide superconductor,showing MR scalable by energy scale.[17]Thus, the violation of Kohler’s rule and the emergence of new scaling usually signals underlying exotic physics,deserving in-depth investigation.

Recent years, twisted Moir´e systems have been demonstrated as an ideal platform hosting lots of unconventional states, such as correlated insulators,[18–24]superconductivity,[19,25,26]ferromagnetism,[27–30]Pomeranchuk effect,[31,32]quantum criticality.[33–35]However,most works in these Moir´e systems focus on emergent ground states in the strong correlated regime,[36]leaving the metallic states and its MR poorly explored.

In this article, we report a study of magnetoresistance behaviors in metal state of twisted double bilayer graphene(TDBG).In TDBG,the Moir´e conduction band(CB)in TDBG is much narrower than the Moir´e valence band(VB),with the former holding correlated states but the latter not.[20–22,37]In addition, the displacement fieldDcouldin situtune Moir´e band bandwidth. Thus, TDBG is a good platform to design contrast experiments in one device to avoid sample variations.We observe quadratic magnetoresistance in both CB and VB.Kohler’s rule is found to be valid in the valence band. By contrast, in the conduction band, we observe a violation of Kohler’s rule and propose an alternative scaling rule near the halo structure. We find a close connection between the violation of Kohler’s rule and the halo boundary.

Firstly,we focus on magnetoresistance data in the Moir´e valence band. Plots of symmetrized longitudinal resistanceRxxagainstBare shown in Fig.1(b),whereRxxincreases from～200 Ω to～2000 Ω nonlinearly as theBchanges from 0 to 2 T, and the curves with lower zero-field resistance have strongerBresponse. By transformingRxxinto magnetoresistance(MR)through MR=[Rxx(B)-R0]/R0and changing thex-axis fromBto the square ofB, the MR curves show quadratic-in-Bdependence at low field,as shown in Fig.1(c).Figure 1(d)shows the Kohler plot of the curves from Fig.1(c).The data from differentDcollapse into one curve, demonstrating the validity of Kohler’s rule in VB. The observation indicates normal metal behaviors in VB. However, the validity of Kohler’s rule is observed in a limited range ofDfrom～0.58 V/nm to～0.74 V/nm (Fig. S3). We think that it is related to complexity of band structure in TDBG,such as van Hove singularity,crossing of VB with CB at lowerD,and valley polarization at higherD.[40]

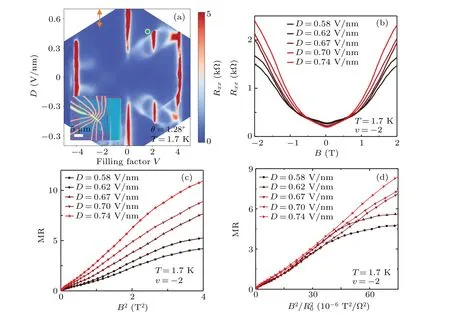
Fig.1. Validity of Kohler’s rule in valence band of 1.28° TDBG.(a)Resistance mapping against filling factor v and displacement field D. The inset shows the optical microscope image of this device. Scale bar: 5 μm. The green dot and orange two-end arrow line mark the position of MR studied in the main text. (b) Longitudinal resistance Rxx against magnetic field at representative D in valence band. (c) MR against the square of B taken from(b). (d)Kohler’s plot of the MR curves in(c).

The quadratic magnetoresistance is also observed in CB of the same device. We focus on magnetoresistance outside the halo structure, and MR inside the halo will be discussed in the supplementary information [Figs. S8(d)–S8(f)]. The halo boundaries atv=1.75 corresponds to displacement fieldDC1=0.417 V/nm andDC2=0.209 V/nm. Figure 2(a)shows plots ofRxx(B) at representativeDthat are larger thanDC1.The anti-symmetrized Hall resistanceRxyat low field is insensitive to the change of displacement field, as shown in Fig. 2(b), ensuring the normal metal state. TheRxxincreases nonlinearly withB,and the increase becomes slower at largerD. The data from Fig.2(a)shows a quadratic MR in Fig.2(c).By doing Kohler’s plot,however,these quadratic curves do not converge to a single plot,implying a violation of Kohler’s rule[Fig.2(d)].

Then we investigate Kohler’s rule further and propose an alternative scaling. For quadratic MR, it followsRxx(B)=A2×B2+R0. The validity of Kohler’s rule requires MR=(A2×B2)/R0∝(B/R0)2, so theB-square coefficientA2should be inversely proportional to zero-field resistanceR0,namelyA2∝1/R0,[1]which is in line with the observation in VB (Fig. S4). By extracting coefficients from Fig. 2,A2andR0are found to be positively linearly correlated in Fig. 3(a),and it leads to the observed violation of Kohler’s rule in CB.What’s more,if we put the linear dependenceA2=C×R0+Finto MR=(A2×B2)/R0,we can reach MR=(C+F/R0)B2.This demonstrates an alternative MR scaling (we call it the“alternative scaling”hereafter for simplicity)based on the observed linear dependence betweenA2andR0. Here we haveC= (0.658±0.035) T-2,F= (-289.69±18.62) Ω·T-2taken from the data in Fig.3(a). Applying this scaling to MR curves in Fig. 2(c), Fig. 3(b) shows all MR curves collapse onto a single one trace at low field,demonstrating the validity of the alternative scaling we suggest. Meanwhile, the scaled trace holds slope about unity,consistent with the requirement of MR=(C+F/R0)B2. We emphasize that the alternative scaling is found to be valid near the halo structure. At an even largerD ＞0.47 V/nm(further away from the halo structure),the resistance becomes insensitive toB(ΔRis the order of several tens of Ω, as shown in Fig. S6), making the scaling unavailable. Morever, the normal metal state at another side of the halo structure(D ＜DC2)in the same device shows the validity of alternative scaling(Fig.S5). Similar behavior is observed in another 1.32°TDBG device,both inside and outside the halo inDdependence,confirming the effectiveness of the alternative scaling(Fig.S8).

Fig.2. Violation of Kohler’s rule in conduction band of 1.28° TDBG.(a)Longitudinal resistance Rxx against magnetic field B at representative displacement fields D,with ε0 being the vacuum permittivity. (b)Hall resistance Rxy against B at representative D corresponding to(a). (c)MR against the square of B taken from(a). (d)Kohler’s plot of the MR curves in(b).

To clarify the origin of alternative scaling in CB,we can discuss about the violation of Kohler’s rule(Fig.2(d))at first.The Boltzmann theory is quasi-classical and based on singleparticle assumption, neglecting quantum mechanical effects and many-body effects. The deduction of Kohler’s rule is based on the idea of the presence of a universal mean free path.[3]Consequently, the violation of Kohler’s rule often results from magnetic breakdown, quantum correction of resistance, anisotropic effects in systems, phonon scattering, and el–el interaction.[1,3,12–16]In this paper,all magnetoresistance data are acquired in the low-field limit(μB ＜1,and no sign of magneto-oscillation is observed),so magnetic breakdown can be safely ruled out. Due to the validity of Kohler’s rule in valence band in the same device,anisotropic effects such as magnetic impurity,strain[41]cannot be the answer. Quantum correction of resistance means weak localization effect or weak anti-localization effect, while no obvious such effect is observed near the halo structure(Fig.2(a)),thus the contribution of quantum correction should be limited. At our base temperature (T～1.7 K), the electron-phonon scattering should not dominate due to the low occupation number of phonons.[42]The violation of Kohler’s rule and the validity of alternative scaling in conduction band may root in el–el interaction near the halo structure.

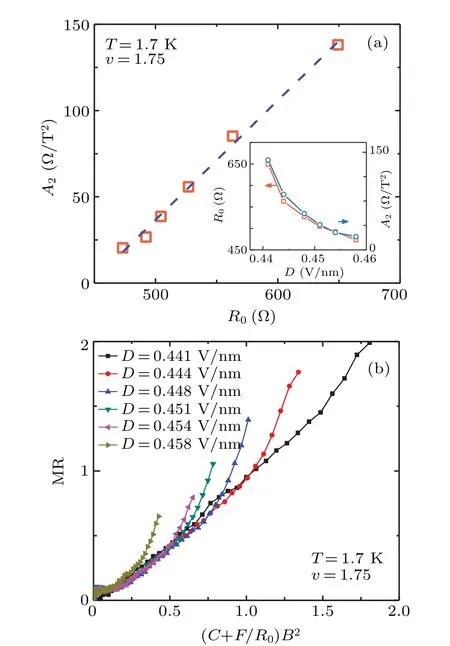
Fig. 3. The alternative scaling of magnetoresistance in TDBG. (a)B-square coefficient A2 against zero-field resistance R0 taken from Fig. 2(a). The blue dashed line shows linear fit between A2 and R0.Inset: A2 and R0 against D used in the main figure. (b)The alternative scaling of MR curves in Fig. 2(c) with linear fitting A2 =C×R0+F.The slope of the scaled trace is about unity, in agreement with the requirement of MR=(C+F/R0)B2 in the main text.

We also find that the quadratic magnetoresistance and alternative scaling in CB are related to the halo boundaries. In our previous work,we found theT-square coefficient of resistance diverges at the halo boundaries(Fig.S7),which signals the enhancement of effective mass at the halo boundaries.[35]Here we demonstrate that the B-square coefficientA2also tends to diverge near the halo boundary where the alternative scaling works [inset of Fig. 3(a), and Fig. 4]. The halo boundary acts as phase boundary of symmetry broken metal state inside it,[37]so we think the quadratic magnetoresistance and alternative scaling root in the critical behavior at the halo boundaries. The specific reason may be el–el interaction enhanced by maximized effective mass there.[35]Recently, an STM study on TDBG reports interaction-driven electronic nematic phase in the normal metal state,[43]in agreement with our hypothesis about the effect of el–el interaction in normal metal state of TDBG. Taking the above discussions together,we suggest that the halo boundaries are relevant to the alternative scaling and the corresponding quadratic magnetoresistance in Moir´e conduction band of TDBG.This is beyond classical Boltzmann theory and calls for future theoretical studies on it.

Fig. 4. The diverging A2 near the halo boundary. The extracted A2 against D near the halo boundary in the 1.32° TDBG device. The A2 tends to diverge as approaching the halo boundary both inside and outside the halo,showing the correlation between the halo boundary. The A2 is taken from MR curves in Fig.S8.

In conclusion, we have studied the magnetoresistance in the metal state of TDBG. The longitudinal resistance shows quadratic-in-Bdependence in the low-field limit in both Moir´e conduction band and valence band. Meanwhile,the quadratic magnetoresistance in Moir´e valence band follows Kohler’s rule, consistent with requirement of classical normal metal.However, we find a violation of Kohler’s rule in conduction band near the halo structure and propose an alternative scaling based on the positive linear dependence betweenA2andR0. Combining the validity of Kohler’s rule in valence band,the quadratic-in-Tresistance and divergingA2near the halo boundaries, we find that the quadratic magnetoresistance and alternative scaling in the conduction band are related to the halo boundaries. The enhanced effective mass near the halo boundaries may be responsible for this finding. Our paper will provide a new perspective to study twisted 2D material systems and quadratic magnetoresistance in condensed matter physics.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (Grant No. 2020YFA0309600), the National Natural Science Foundation of China (Grant Nos. 61888102, 11834017, and 12074413), the Strategic Priority Research Program of CAS(Grant Nos. XDB30000000 and XDB33000000), and the Key-Area Research and Development Program of Guangdong Province (Grant No. 2020B0101340001). Growth of hexagonal boron nitride crystals was supported by the Elemental Strategy Initiative conducted by the MEXT, Japan,Grant Number JPMXP0112101001, JSPS KAKENHI (Grant No.JP20H00354)and A3 Foresight by JSPS.