竖直平面内圆周运动引起系统离地问题分析

唐小平

(贵州省遵义市桐梓县桐梓二中)

在高中物理阶段,有一类比较特殊的物理问题:某个物体在竖直平面内做圆周运动,引起整个系统离地.

模型如图1所示,一个电动机质量为M,在其转轴上用长为r的刚性绳固定一个质量为m的物体,为使电动机不跳离地面,其转轴转动的角速度最大应为多少?

图1

分析根据日常经验,我们可以判断出,当物体转到最高点时,若物体对转轴的作用力恰好等于电动机的重力,电动机受力平衡,这时转轴的转速是临界值;当转轴转速大于这个转速时,电动机跳离地面.我们只需求出这个临界角速度就可以解决问题.

解当电动机刚要跳离地面时,物体运动到最高点,物体对飞轮的作用力F恰好等于电动机的重力Mg,得F＝Mg.以物体为研究对象,由牛顿第二定律可得Mg＋mg＝mω2r,解得ω＝

以上就是本文要讲的问题的典型表现形式和常见解题方法.但是,物体跳离地面的临界条件真的就是做圆周运动的物体运动到最高点时吗? 下面我们以例题为证,看看临界条件究竟如何确定.

例1如图2所示,在水平地面上有一个质量为M的立方体,它的内部中心有一个半径为R的竖直圆槽,一个质量为m的小球放在槽底.若小球与圆槽之间光滑无摩擦,给小球一个水平向右的初速度v0,之后小球沿圆槽做周期性变速圆周运动,立方体始终静止在地面上.当初速度v0分别取时,求立方体对地面的最小压力.

图2

错解小球运动到最高点时,立方体对地面的压力最小.设小球到达最高点时的速度为v,小球由最低点到最高点时,由机械能守恒定律可得

分析以上解法貌似正确,其实犯了两个非常大的错误:其一,没有判断小球能够运动到最高点所需的最小初速度的大小;其二,主观认为小球运动到最高点时就是立方体对地面的压力最小时.第一个错误,很多学生能够避免,第二个错误却是绝大多数学生的常见认知,他们忽略了影响立方体对地面压力大小的因素是小球与立方体间作用力的竖直分量的大小.

正解设小球恰好运动到最高点时速度为v,则有mg＝,解得v＝,根据机械能守恒定律得,解得v0＝.由此可判断题给两个初速度情况下小球均能到达最高点.

如图3 所示,设小球运动到与竖直方向的夹角为θ时速度大小为v,立方体对小球的作用力为FN,则由机械能守恒定律和牛顿第二定律得

图3

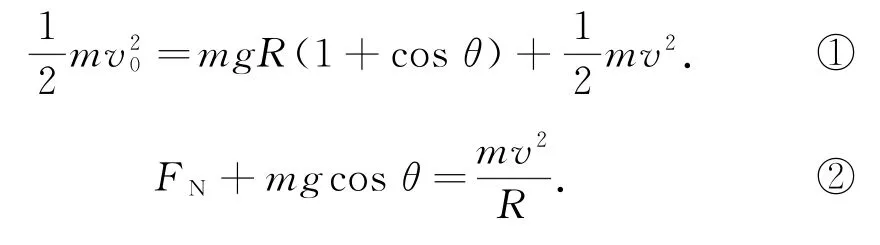
解得

则小球对立方体的作用力

由以上计算可知,立方体对地面的压力最小时,小球的位置与其初速度有关,并非总是在小球运动到最高点时.

例2如图4所示,半径为r的圆形光滑导轨A竖直放置并固定在木板B上,木板B无法左右移动但可以向上无阻碍运动.有一个小球静止放在圆形导轨底部.小球、导轨A和木板B的质量均为m.给小球一个水平向右的初速度v0,为保证小球能够运动到导轨最高点,同时木板B不离开地面,则小球的初速度v0可能是().

图4

分析本题涉及两个临界值.其一,当小球运动到轨道最高点时速度为是初速度v0取最小值的临界条件,此时v0＝;其二,小球对轨道的竖直向上的作用力恰好等于2mg,是木板恰好离开地面的临界条件.

解如图5所示,设小球运动到与竖直方向的夹角为θ时速度大小为v,导轨对小球的作用力为FN,则由机械能守恒定律和牛顿第二定律得

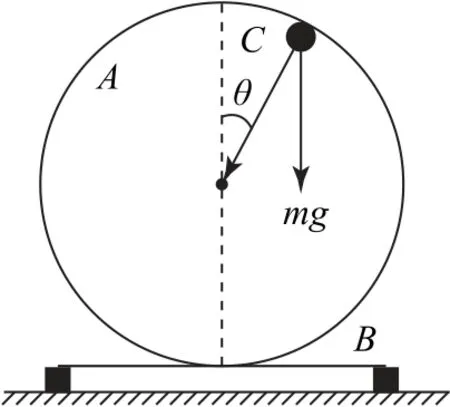
图5

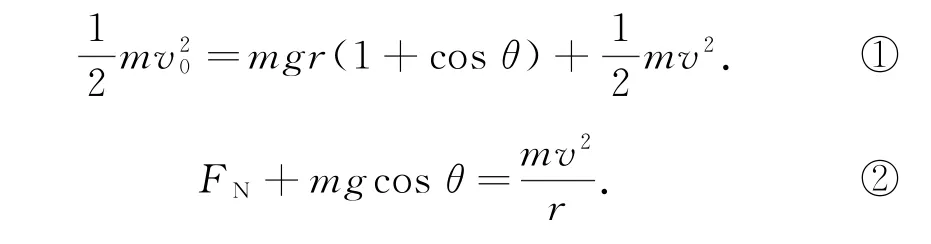
以导轨和木板为整体,设二者的质量为M,要使木板不离开地面,有

联立式①②③可得

通过以上分析,我们可以知道,当某个物体在竖直平面内做圆周运动引起另一物体离地时,不可主观判断,必须通过缜密的分析计算,才可得到准确结果.

(完)