转盘类圆周运动归类赏析
2022-10-26胥红斌
胥红斌
(甘肃省天水市秦安县第一中学)
转盘背景下的运动模型一般有三种.不同模型的质点运动存在临界问题和最值问题,本文就此类问题进行剖析与拓展,探究解决此类问题的通性通法.
1 转盘类圆周运动及其分类
转盘之上放置一个物体、两个物体或多个物体围绕转盘中心转轴转动,物体之间或利用绳子牵连,或叠加放置,要求考生分析物块的受力与运动状态的问题统称为转盘类圆周运动问题.根据转盘上物块个数多少可以将它们分成三类:单质点转动模型、双质点转动模型和多质点转动模型,也可根据转盘上物体的空间连接方式分为独立转动模型、叠加体转动模型、绳牵连转动模型.
2 转盘类圆周运动的呈现方式
2.1 单质点转动模型
当一个物体放在转动的圆盘上转动时,圆盘对物体的摩擦力将提供物块运动所需要的向心力,当转盘的角速度缓慢增加时物块受到的摩擦力将逐渐增加.
例1如图1所示,一可视为质点的物体随转盘一起围绕转盘中心转轴匀速率转动,当转速缓慢增加时,关于物块的运动和受力说法正确的是().
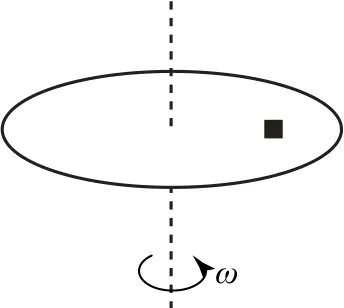
图1
A.物块所需的向心力大小保持不变
B.摩擦力的方向与线速度的方向相反
C.物块受到重力、支持力、摩擦力和向心力
D.摩擦力是物块运动向心力的来源
解析物体在转盘上受到重力、支持力和摩擦力,其中重力和支持力保持平衡,在物块未和转盘发生相对滑动之前摩擦力提供圆周运动所需向心力,方向始终指向运动中心并且随着转速增大而增加.故选 项D 正确.
点评上述案例是单质点转动模型中较为简单又典型的试题,分析向心力的来源是处理这类问题的关键,而受力分析则是解题关键.分析本题需要关注两点:其一,需要紧扣“转速缓慢增加”这一题眼,“缓慢”二字的潜在意义就是只要物体没有发生相对滑动,物体在任何状态下的运动都可以看作匀速圆周运动;其二,重力和支持力是一对平衡力,静摩擦力是向心力的效果来源,因而其方向指向运动中心,且它随着角速度的增加而逐渐变大,直至物体与转盘发生相对滑动.
2.2 双质点转动模型
我们把两个可以看成质点的物体随转盘转动的模型称之为双质点转动模型.这两个物体的组合形式可以是单独存在于转盘之上,也可相互叠加形成叠加体,也可以通过绳子相连接形成牵连体等.分析这类问题的主要方法是整体法和隔离法.
例2如图2所示,质量不等的甲、乙两个物块放在水平转盘上,两物块与转盘之间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,让转盘绕过圆心的竖直轴匀速转动,并逐渐增大转动角速度,发现甲物块先滑动,其原因是().

图2
A.甲的质量比乙小
B.甲的质量比乙大
C.甲离转轴的距离比乙小
D.甲离转轴的距离比乙大
解析甲物块先滑动说明甲先于乙达到最大静摩擦或者临界加速度,即μmg=mrω2=mr·4π2n2或μg=rω2=r·4π2n2,在甲相对转盘滑动之前甲、乙转速一样,哪个物块先滑动与物块的质量无关,只与它们距离中心转轴的距离有关,距离远的最先滑动,距离近的稍后滑动.故选项D 正确.
点评假设甲、乙到中心转轴的距离分别是r1、r2,滑动摩擦因数为μ.对甲而言μm甲g=,甲开始滑动时转盘的角速度ω1=,此时乙所受到的摩擦力,还未达到最大静摩擦力,因此它相对转盘保持静止.当时,乙才与转盘开始发生相对滑动.本题的易错点在于,考生容易认为质量小的物块最先滑动,质量大的物块最后滑动,把物块质量与滑动本质对应.对于这样的问题,教师需要引导学生一步一步挖掘题中的隐含条件进行临界分析,帮助考生厘清问题解决的方向,从本质上来讲,此题与例1差别并不大,分析思路大同小异.
2.3 三质点转动模型
我们把转盘上有三个随转盘一起转动的物块的情形称之为三质点转动模型.在习题教学中最常见的是绳牵连与叠加的情形,这类问题都可以通过一些物理处理变为双质点转动模型,这类题型虽情境单一,分析过程却较为复杂.
例3如图3 所示,在水平转盘上放有质量分别为m、m、2m的可视为质点的三个物体A、B、C.圆盘可绕垂直圆盘的中心转轴O1O2转动,三个物体与转盘之间的动摩擦因数均为μ,最大静摩擦力等于滑动摩擦力,三个物体与轴心O共线且OB=OA=BC=r.现将三个物体用轻质细绳相连接,保持细线伸直且恰好无张力,重力加速度为g,圆盘从静止开始转动,角速度ω极其缓慢地增大,对于这个过程,下列说法正确的是().

图3
A.A、B两个物体所受的摩擦力同时达到最大静摩擦力
B.B、C两个物体所受的静摩擦力先增大后不变,A物体所受的静摩擦力先增大后减小再增大
C.当ω=时,三个物体整体发生滑动
解析转动伊始,摩擦力提供运动所需向心力,FfA=FfB=mrω2,FfC=2m·2rω2=4mrω2,随着角速度的增加,物块所需向心力大小也将增加,当FfC=μ·2mg时,B、C之间的绳子即将产生张力,对C根据μ·2mg=,得ω1=,此时A、B还未达到最大静摩擦力,A、B之间的绳子还未产生张力.
转盘转速进一步增大,B、C之间的绳子产生张力.对C有FTBC+μ·2mg=4mrω2,对B有FfBFTCB=mrω2,对A,FfA=mrω2,可知B先于A达到最大静摩擦力,当FfB=μmg时,A、B之间的绳子即将产生张力,此时对B、C分别有μmg-FTCB=,FTBC+μ·2mg=,解得ω2=,此刻以后随着转速的增加,A、B之间的绳子产生张力,对B有FTAB+μmg-FTCB=mrω2,再利用假设法对A有FTBA+FfA=mrω2,根据C的方程解出B、C绳上的张力FTBC=4mrω2-2μmg,代入前两式得到FfA=3μmg-4mrω2,那么我们便得到当ω>ω2之后FfA随着角速度的增加先减小为零,再反向增加到μmg,此时对A有FTBA-μmg=,解得ω3=.故选项B、C、D 正确.
点评在本题求解的过程中,我们需要认真考虑物体的临界状态,分阶段列出牛顿第二定律,整个过程始终要关注物体是否达到了最大静摩擦力以及绳子究竟处于哪种状态.
3 方法总结与整理感悟
1)寻找向心力来源和对物块进行状态分析是解决这类问题的方向.不管转盘上的物块及其组成结构多么复杂,只要它们所做的运动可以看成匀速圆周运动,那么解题方向就是通过受力分析准确找到向心力来源,然后再根据物块的运动验证受力分析的正确性.
2)恰当的归类和变式可以提升复习的整体效能.试题归类拓展可以让知识“结网”,让零散的知识形成“知识块”.变式分析则增强了思维的灵活性,通过变式应用,学生对解题技巧的掌握会更加牢固.
总之,深度研究转盘类问题不仅能够促成知识学习向深度理解的转换,还能够增强学生知识结构的网络化程度,当学生能够按照知识分类的角度思考问题时,学生的学习能力也就逐步得到加强.
(完)
