鞍点问题解的存在性

蒋源鑫,刘奇鑫

（重庆交通大学 数学与统计学院,重庆 400074）

引言

鞍点问题在数学规划和博弈论的研究中占有非常重要地位。它为极大极小问题、拉格朗日对偶问题、变分不等式、Nash 均衡问题的研究提供了有效的表述形式和基本工具。目前鞍点问题的理论研究主要是集中在鞍点的存在性[1-9]。其中,Karamardian[11]通过对目标函数的拟凸拟凹假设,得到了定义在紧凸集上的鞍点问题解的存在性。Iusem[12]等人则通过渐进分析与对目标函数的拟凸拟凹假设,得到了定义在闭凸集上的平衡问题解的存在性与解集紧性。受上述研究的启发,研究了定义在闭凸集上的鞍点问题解的存在性,并在适当的假设条件下,给出了鞍点的存在性条件以及解集的相关性质。

1 预备知识

为了方便起见,我们用S(C,D,f)表示（SPP）所有鞍点组成的集合。下面给出二元函数凸性与凹性的定义[10]。

定义1,假设C⊂R�和均为非空凸子集。

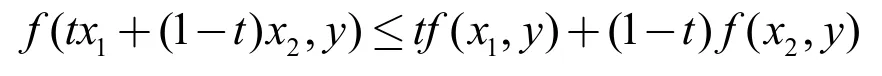
则称二元实值函数f:C×D→R 在C 上关于x是凸的,反之亦然。

（2） 若对于 ∀x∈C, ∀y1,y2∈D, ∀t∈［ 0,1］,有

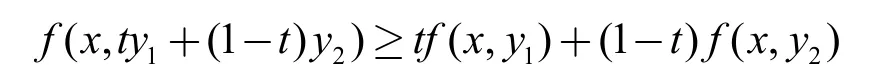
则称二元实值函数f:C×D→R 在C 上关于y是凹的,反之亦然。

定义2,假设C⊂Rn和D⊂R�均为非空凸子集。

则称二元实值函数f:C×D→R在C 上关于x是拟凸的,反之亦然。

（2） 若对于 ∀x∈C,∈D, ∀t∈［ 0 ,1］,有

则称二元实值函数f:C×D→R 在C 上关于y是拟凹的,反之亦然。

注1,所有的凸函数都是拟凸函数,所有的凹函数都是拟凹函数,反之不一定成立。例如,假设C 和D 均为 R 的非空凸子集,则对任意的y∈D,f(x,y) =,x∈C为C 上的拟凸函数,但不是C 的凸函数。

下面给出二元函数上半连续性与下半连续性的定义[10]。

定义3,假设C⊂Rn和D⊂Rm均为非空凸子集,f:C×D→R 为二元实值函数。

（1） ∀y∈D,若对任意收敛到x 的序列｛｝ ⊂C,有f(x,y) ≤f(,y),则称f 在x∈C处是下半连续的,若对任意的x∈C都成立,则称f 在C 上是下半连续的。

（2） ∀x∈C, 若对任意收敛到y 的序列 ｛｝⊂D,有f(x,y) ≥f(x,),则称f 在y∈D处是上半连续的,若对任意的y∈D都成立,则称f 在D 上是上半连续的。

引理1[11],设C⊂Rn,D⊂Rm为紧凸集,且f 为定义在C×D 上的实值函数,假设下列条件成立：

（1） 当固定y∈D时,f 为C 上的下半连续拟凸函数；

（2） 当固定x∈C时,f 为D 上的上半连续拟凹函数；

本文主要考虑的是借助函数f 的一致性以及渐进性,将上述的经典结论推广到非紧的情况下。下面给出关于函数一致性的定义。

定义4[13],假设C⊂Rn,D⊂Rm均为非空子集,f:C×D→R 为二元实值函数。任取(y1,y2) ∈D×D,存在x0∈C使得

则称f 在C 上具有一致性。

定义5[12],假设,D⊂Rm均为非空子集,f:C×D→R 为二元实值函数。假设u∈Rn:u≠0,v∈Rm:v≠0和 ∈ R := { ∈ R ＞0}。

（1） f 关于x 的渐进函数定义为

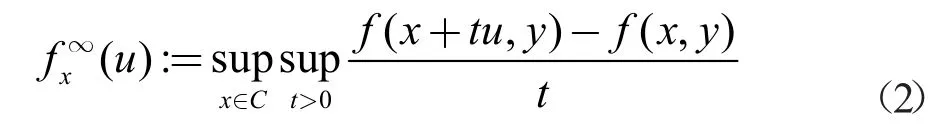
（2） f 关于y 的渐进函数定义为

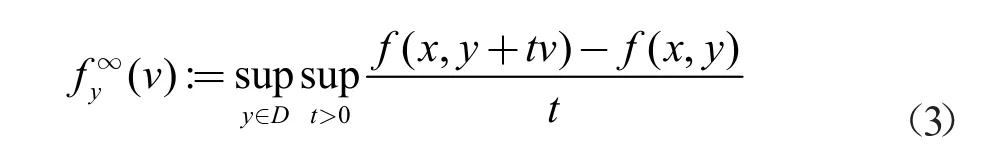
定义6[14],假设C 为中的非空子集,C 的渐进锥C∞定义为

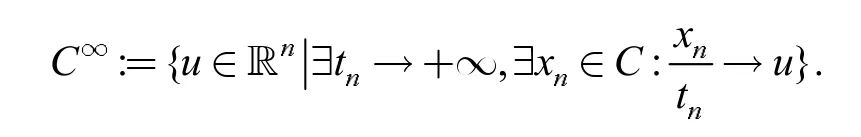
2 主要结果

为了讨论鞍点问题解的存在性,需先建立如下的辅助结果。

命题1,如果f:C×D→R 有界,则对于任意的,,有

定理1,设C⊂R n,D⊂Rm为闭凸集,且f 为定义在C×D上具有一致性的实值函数,假设下列条件成立：

（1） 当固定y∈D时,f 为C 上的连续拟凸函数；

（2） 当固定x∈C时,f 为D 上的连续拟凹函数；

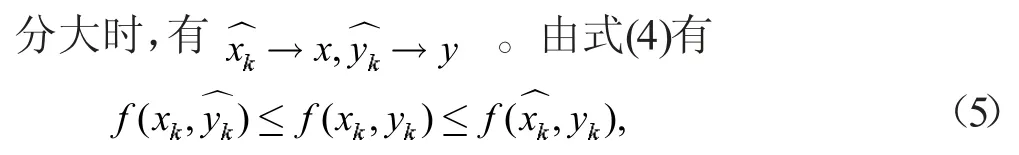
因为f 在C,D 均具有一致性,所以由式(1)和式(5)可以推出

由假设条件（1）可知,任意固定y∈D,f 为D 上的连续拟凹函数,因此

由假设条件(2)可知,任意固定x∈C时,f 为D 上的连续拟凹函数,因此