交流永磁力矩电机高过载状态下的转矩波动研究
2022-10-25岳通魏国王骞余潇雷晗
岳通,魏国,王骞,余潇,雷晗
交流永磁力矩电机高过载状态下的转矩波动研究
岳通1,魏国1,王骞2,余潇1,雷晗1
(1.中国兵器工业第二〇九研究所,四川 成都 610041; 2.哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001)
交流永磁力矩电机具有转矩密度高、控制精度高、免维护等特点,转矩平稳性是其关键指标之一。本文采用有限元法对交流永磁力矩电机在不同负载状态下(轻载、额定负载、高过载)的转矩波动进行研究,并揭示转矩波动与饱和之间的变化规律。研究结果表明:交流永磁同步电机的转矩波动与负载程度密切相关;随着负载的增大,转矩波动峰值和转矩波动系数均呈现先上升后下降再上升的变化趋势;电磁转矩波动幅值明显高于总体转矩波动,只能反映总体转矩波动的趋势;负载齿槽转矩峰值的变化趋势和电磁转矩波动的规律几乎相同,也可当做判断总体转矩波动的一个参考值。
交流永磁力矩电机;过载;转矩波动
交流永磁力矩电机具有转矩密度高、体积质量小、控制精度高、布置灵活、免维护等特点,在航空航天、国防武器、高技术船舶、机器人等领域具有广泛的应用。交流永磁力矩电机技术的应用,提高了运动控制系统的控制精度和响应速度,已成为国航和航天领域重要的支撑技术[1-3]。
在交流永磁力矩电机系统中,转矩平稳性是一项关键指标。然而,由于反电势或电流的非正弦特性,以及齿槽定位力矩等因素的存在,交流永磁力矩电机的输出转矩不可避免地会存在波动[4-7]。电机的转矩波动将使运动系统出现转速波动、谐振或噪声,影响系统的可靠性、控制精度或舒适性等重要指标。因此,对交流永磁力矩电机系统的转矩波动进行分析和抑制具有重要意义。
目前,对交流永磁力矩电机系统的转矩波动已有较多研究,基本揭示了转矩波动的成因,并指出可从电机本体和驱动控制两方面入手来有效抑制转矩波动[8-11]。然而,目前的研究多集中在轻载或额定状态下的电机转矩波动分析,鲜有文献对力矩电机高过载状态下的转矩波动进行研究。事实上,一方面,高过载是交流永磁力矩电机一个重要的运行状态,它直接影响装备的机动性和动态运行品质;另一方面,在高过载下,由于磁路饱和程度的增加,电势谐波含量加剧,造成转矩波动严重,并可能导致传统的转矩波动抑制方法失效。因此,对交流永磁力矩电机高过载状态下的转矩波动进行研究,具有重要意义。
本文基于磁共能法对电磁转矩的组成成分进行分析,采用有限元计算对交流永磁力矩电机在不同负载状态下(轻载、额定负载、高过载)的转矩波动进行研究,并引入转矩波动系数揭示转矩波动与饱和之间的变化规律。
1 电磁转矩的组成成分分析
在空载情况下,交流永磁力矩电机的转矩表现沿零值上下波动的齿槽转矩,其表达式为:
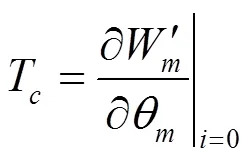
齿槽转矩主要是由转子磁场和定子随转子旋转变化的磁阻之间的相互作用产生,本质上反应的是磁场能量随转子运动而发生的变化。由于齿槽转矩在一个周期内的平均值为零,因此对电机的功率输出没有贡献。
在负载条件下,电机的稳定电磁转矩可表示为:

由式(2)可知,电机输出转矩可以分为电磁转矩和磁场储能变动引起的转矩,其中:


若三相电机在0坐标系下分离电磁转矩,则:



综上所述,在坐标系和0坐标系下,电机的转矩都可以分为三部分:PM转矩、磁阻转矩和负载齿槽转矩。对于这三部分转矩分量,任何一个分量发生变化,则总的转矩都将出现波动。
2 过载对转矩波动的影响分析


表1 电机主要参数
为提高电机的转矩平稳性,通常手段是优化电机磁钢的形状,如图2所示。这样一方面可以降低空载时电机的5、7次反电动势谐波,从而一定程度上降低电磁转矩波动;另一方面,由于磁钢两侧边缘做成多段圆弧形状,当电机运行时可以减缓磁场能量的变化,从而降低齿槽转矩。由于这两个原因,轻载时的电机转矩平稳性会得到显著提高。需要说明的是,此时电枢反应磁场较弱,由其感生出来的反电动势谐波可以忽略不计,因此可以近似认为电磁转矩波动主要是由空载反电动势谐波引起,而齿槽转矩也为空载齿槽转矩。

图1 磁钢优化前后的形状对比
对该电机建立有限元模型,如图2所示。不断调整磁钢的几何参数,使得磁钢优化后空载相反电动势的5、7次谐波分量的谐波畸变率降低。最终确定下来的磁钢,其对应的反电动势频谱如图3所示。
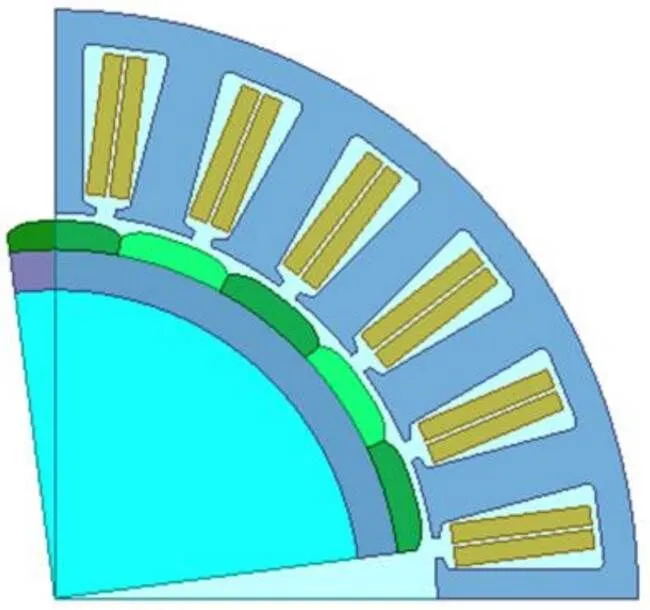
图2 电机有限元计算模型

图3 相反电势频谱图
可以看出,此时电机反电势5、7次谐波幅值几乎为零。实际上此时的谐波畸变率已经降低到0.1%以下。
2.1 空载/轻载时的转矩波动
对该电机进行二维有限元分析,得到在空载和轻载时,优化磁钢前后的转矩波动波形如图4所示。可以看出,优化磁钢之后,空载条件下和轻载条件下,转矩的波动程度都远低于优化之前。优化后,空载时转矩峰峰值为优化前的2.3%,轻载(=20 A)时则为8.6%。
2.2 高过载状态时的转矩波动
随着负载的增加,输入电流随之增大,此时由于电枢磁动势的增加以及漏磁等因素的影响,定子铁芯的各区域会出现不同程度的饱和。空载和额定负载两种工况下电机的磁密云图对比如图5所示。
可以看出,相对于空载,在额定负载状态下,齿部和轭部的磁密幅值明显增加,达到1.6~1.8 T。而齿尖部分更甚,其磁密幅值超过了2.0 T,如图6所示。

图4 磁化优化前后的转矩波动波形对比

图5 电机磁密云图
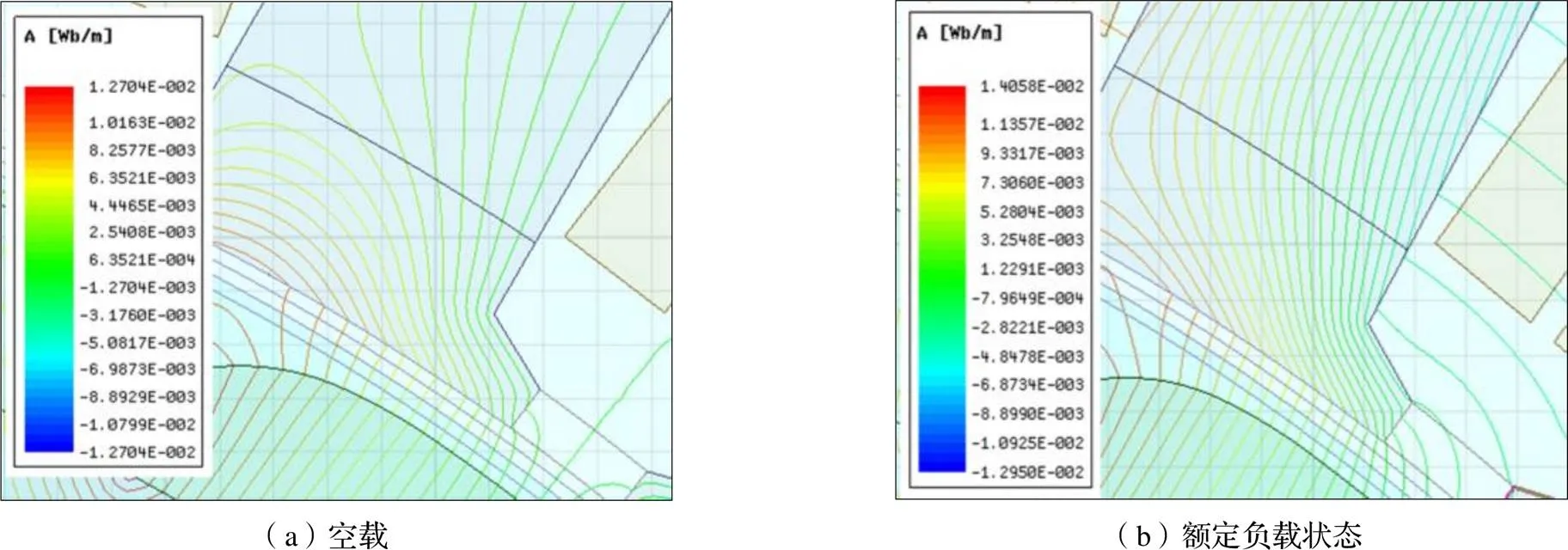
图6 电机齿尖处的磁力线分布图
事实上,空载时齿尖部分就存在一定程度的饱和,这主要是齿的聚磁效应引起的。在负载情况下,齿尖部分饱和更加严重,一方面是由于电枢磁动势增加,定子铁芯的磁密整体增大,另一方面则是由于齿尖产生漏磁现象,加剧齿尖的饱和。额定负载条件下的齿尖漏磁明显高于空载。
随着电流的增加,铁芯饱和程度随之增加,这将直接影响输出转矩-电流的线性度,如图7所示。可以看出,在远低于额定电流的区域,实际转矩-电流曲线与图中表征线性关系的虚线非常接近;当电流接近及超过额定点时,实际曲线逐渐偏离线性曲线,输出转矩与电流不再成比例关系,且低于理想的线性转矩。
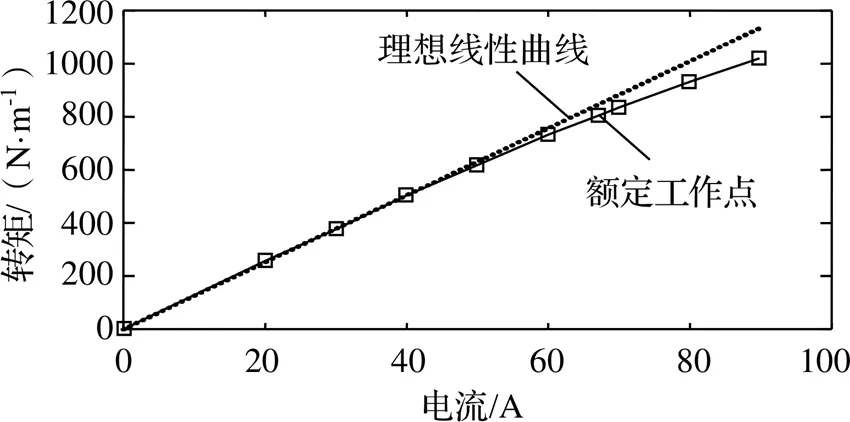
图7 电机转矩-电流曲线
3 转矩波动系数
优化磁钢形状的方法,在轻载工况下能很好地提高电机的转矩平稳性,然而随着铁芯饱和程度的增加,其转矩波动的抑制效果会大打折扣。一方面,饱和会增加反电动势的5次和7次谐波分量,增加电磁转矩的波动量;另一方面,会影响负载齿槽转矩的幅值和相位。从总的趋势来说,饱和程度的增加会增大转矩波动的幅值,削弱优化磁钢形状带来的好处。
为了考察转矩波动与饱和之间的关系,这里用转矩波动系数来描述转矩波动的程度:

优化磁钢形状之后的转矩波动峰峰值和转矩波动系数随电流的变化如图8所示。
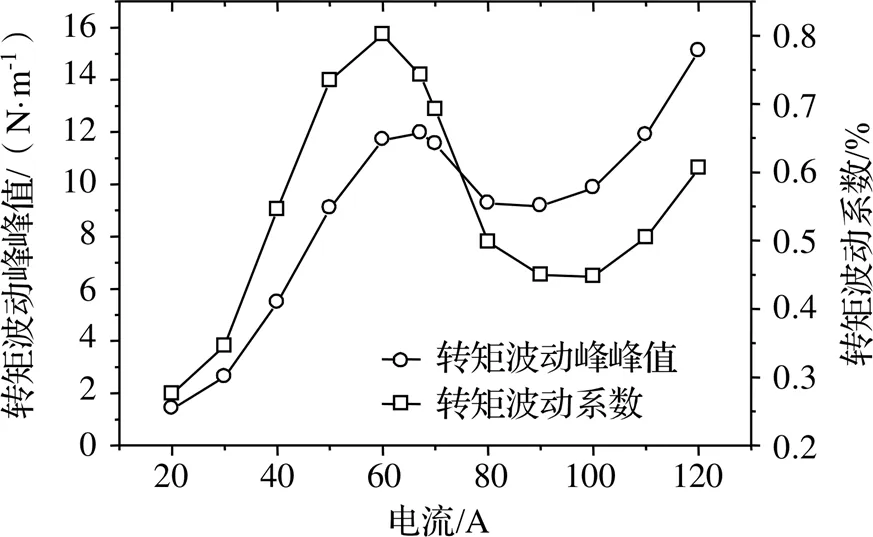
图8 转矩波动峰峰值和转矩波动系数随电流的变化
可以看出,随着电流的增大,转矩波动的峰峰值和转矩波动系数整体都呈现上升趋势,但是转矩波动峰峰值曲线上升到额定电流(67.2 A)附近出现了拐点,拐点过后呈现下降趋势,在90 A附近达到最小值,此后曲线随电流的增大仍然呈现上升趋势。
针对图8中的曲线选择具有代表性的加载电流值,计算它们对应的转矩波动波形,得到图9,并进行傅里叶变换,得到不同电流下转矩波动的6次和12次分量的幅值和相位,如图10所示。
由图10(a)可以看出,电流从67.2 A上升到110 A时,转矩波动的6次分量幅值一直在降低,12次分量则先下降后上升,且上升幅度很大。由图10(b)可以看出,不同电流下转矩波动的6次和12次分量的相位差均在90°~270°之间。因此,从转矩波动的峰值来看,6次和12次分量存在一定的相互抵消作用。因此,图8之所以在转矩波动峰峰值上升的总趋势中出现下降的现象,主要是因为6次和12次分量存在此消彼长的竞争作用。随着电流的继续增长,在120 A位置处,6次和12次分量的幅值相对于110 A均有所上升,并且两者之间的相位已经低于90°,因此两者的峰值并不存在抵消作用,反而具有一定的叠加效果。

图9 不同电流时的转矩波动波形

图10 不同电流下转矩波动的6次和12次分量
4 过载对转矩波动分量的影响
采用冻结磁导率技术(Frozen Permeability,FP)分离电机的电磁转矩和负载齿槽转矩。原理如图11(a)所示,当不使用冻结磁导率技术时,在只有PM激励即开环时,磁场强度为PM,对应的磁通密度为PM(点);在只有电流激励时,磁场强度和磁通密度分别为i和i(点)。在额定负载条件下(点),总的磁场强度为PM磁场强度和电流磁场强度的叠加,即PM+i=all。然而总的磁通密度all却比PM+i要低。因此负载情况下的PM和电枢反应磁场无法分离。当使用冻结磁导率法时,首先计算负载磁场(点)得到负载时的磁导率all,并且将该值存储在各个单元的数据中。然后利用上述磁导率做线性有限元计算,分别分析点和点的磁场,即只有PM激励的磁场(FP, PM)和只有电流激励的磁场(FP, i)。通过冻结磁导率,非线性问题已经转换成线性问题,所以all=(FP, PM)+(FP, i),从使得负载情况下的PM和电枢反应磁场得到分离。
根据前面的分析,对有限元中冻结磁导率法的步骤进行总结,如图11(b)所示。首先使用非线性有限元分析负载情况的磁场,然后存储各个单元中的磁导率,最后使用上述磁导率对PM和电流单独激励时的磁场分别进行线性有限元分析。

图11 冻结磁导率法的原理和步骤
利用式(2)、式(3)对电机的输出转矩进行分离,只需要计算总转矩、电磁转矩和负载齿槽转矩这三个变量中的两个即可。由于负载齿槽转矩需要计算常值电流情况下的磁场能量微分,并且磁场能量是由各个单元的能量累加得到,所以实现起来不方便,且计算误差较大,难以满足要求。因此,选择计算总转矩和电磁转矩,利用二者之差即可得到负载齿槽转矩。利用非线性有限元静磁场功能计算不同时刻电机负载情况下的总转矩,得到负载时的绕组磁链,并对该磁场冻结磁导率,然后利用线性静态磁场功能计算每一时刻的只有PM激励和只有电流激励两种情况下的磁链,由此可以得到以上三种情况下的每相反电动势为:
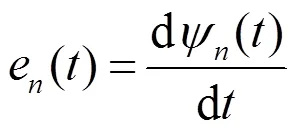
最后利用式(2)、式(3)分离各个转矩分量。
分别计算空载和额定负载条件下的电磁场,得到反电动势时域波形,如图12所示。由图12(a)可知,因饱和影响,相对于空载磁场,负载PM磁场感生的反电动势产生了扭曲,并且负载时电枢磁场感生的反电动势也非常明显,其幅值和PM磁场感生的反电动势相当。将负载时PM磁场感生的反电动势和电磁磁场相加,可以得到负载时总的反电动势,如图12(b)所示。电枢反应使得负载反电动势相对于空载幅值明显有所增加,并相位也有所改变。磁场饱和使负载反电动势发生了明显的扭曲。

图12 空载和负载反电动势
通过快速傅里叶分析得到反电动势谐波频谱,如图13所示,可以看出,负载的反电动势无论是基波还是谐波均有所增加,特别是5次和7次谐波,幅值分别为空载时的36.9倍和24.1倍。根据公式计算可知,5次和7次谐波畸变率为3.1%,实际上负载时11次和13次等其他谐波幅值也很明显,总谐波畸变率高于3.1%。

图13 反电动势频谱
根据前面的分析可以预见,电磁转矩波动的幅值会因为反电动势谐波的增加而增大。实际上额定负载时的电机各转矩波动分量的时域波形如图14所示。其中图14(b)所示的PM转矩波动和磁阻转矩波动波形显示两者的峰峰值要比实际总转矩波动还要大一些,并且两者的基频均为电频率的6倍,与前面的分析吻合。与此同时,图14(a)显示,负载齿槽转矩相对于空载,其峰峰值由原来的0.27 N·m变成现在的53.8 N·m,波动程度甚至超过了PM转矩波动和磁阻转矩波动。可见负载齿槽转矩对负载时的转矩波动起到了重要作用。由于负载时存在电枢磁场和饱和效应,负载齿槽转矩的基波周期也由原来的30°电角度变成现在的60°电角度。因此,在PM转矩波动、磁阻转矩波动和负载齿槽转矩波动的基波次数均为6次的情况下,输出转矩自然也就呈现出以6次为基频的波动。
利用冻结磁导率技术分离不同负载条件下的转矩分量,可得到各转矩分量的波动随电流的变化,如图15所示。其中图15(a)的纵轴为实际转矩波动的峰峰值,图15(b)的纵轴为转矩波动峰峰值占其各自最大值的百分比。可看出,各转矩分量的波动峰峰值总体呈现随电流增加而增大的趋势,且各转矩分量增加的速度大于总转矩。由于各转矩分量存在如图14所示的相位差,因此虽然各分量波动幅值迅速上涨,总转矩波动的幅值却明显低于各转矩分量。特别需要指出的是,PM转矩和磁阻转矩波动的峰峰值均单调增加,并不能反映总转矩波动幅值的变化趋势,但两者之和,即电磁转矩波动的增长趋势却和总体转矩波动相同。根据式(2)和式(3),只有使用负载时总的绕组反电动势计算得到的电磁转矩波动才能反映总体转矩波动的趋势,而只用PM感生的反电动势却不能。但即使如此,电磁转矩波动也只能反映总体转矩波动的趋势,其幅值明显高于总体转矩波动。另外,负载齿槽转矩峰峰值的变化趋势和电磁转矩波动的规律几乎相同,因此也可以当作判断总体转矩波动的一个参考值。
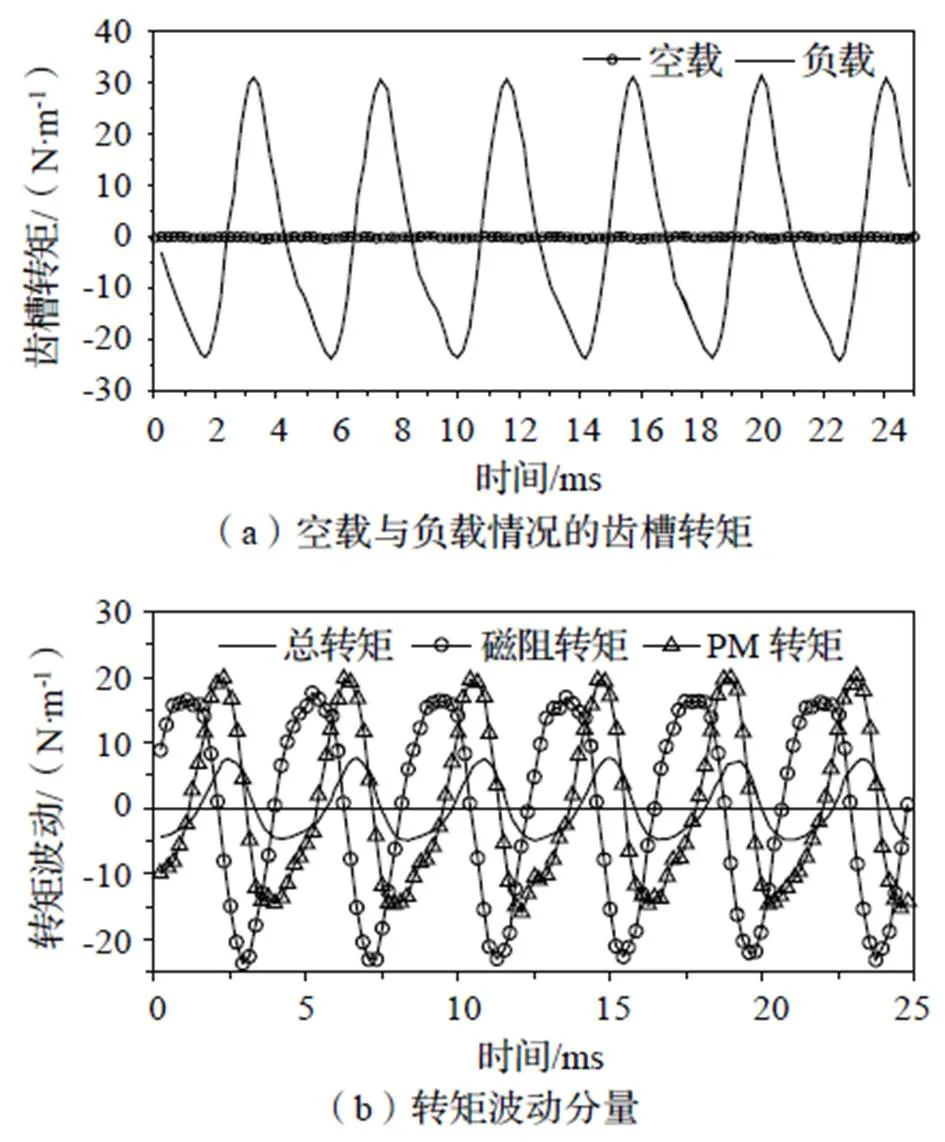
图14 空载和额定负载时的转矩波动分量
5 结论
本文对交流永磁同步电机在高过载运行状态下的转矩波动进行了计算和分析。通过以上研究,得出如下结论:
(1)交流永磁同步电机的转矩波动与负载程度密切相关。
(2)随着负载的增大(从空载到过载),转矩波动峰峰值和转矩波动系数均呈现先上升后下降再上升的变化趋势。
(3)电磁转矩波动幅值要明显高于总体转矩波动,只能反映总体转矩波动的趋势。负载齿槽转矩峰峰值的变化趋势和电磁转矩波动的规律几乎相同,也可以当作判断总体转矩波动的一个参考值。
本文研究可为同类电机转矩波动的分析与抑制提供一定的指导。

图15 转矩波动随电流的变化
[1]鲍晓华,刘佶炜,孙跃,等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报,2019,34(6):1148-1160.
[2]陈强,王骞,徐永向. 大力矩、低脉动交流永磁力矩电机设计[J]. 电机与控制应用,2017,44(9):39-43.
[3]Chai Jiawei,Zhao Tianyi,Gui Xianguo. Multi-Objective Optimization Design of Permanent Magnet Torque Motor[J]. World Electric Vehicle Journal,2021,12(3):1-14.
[4]M. S. Islam,S. Mir,T. Sebastian,et al. Design considerations of sinusoidally excited permanent-magnet machines for low-torque- ripple applications[J]. IEEE Trans. Ind. Appl.,2005,41(4):955-962.
[5]王成刚,晏芙蓉,何凡,等. 永磁同步电机的振动控制分析[J]. 机械,2016,43(11):1-3,9.
[6]付学敏. 分数槽永磁电机空间谐波定量分析及转矩波动抑制研究[D]. 合肥:安徽大学,2013.
[7]李碧政,张继鹏. 高精度转台永磁无刷力矩电机力矩波动分析[J]. 价值工程,2019,38(28):191-193.
[8]钱荣超,孙兆琼. 超低转动惯量无刷力矩电动机电磁及结构设计[J]. 微特电机,2019,47(3):29-31.
[9]Zhang Q,Yan L,Duan Z,et al. High Torque Density Torque Motor With Hybrid Magnetization Pole Arrays for Jet Pipe Servo Valve[J]. IEEE Transactions on Industrial Electronics,2020,67(3):2133-2142.
[10]Thomas M. Jahns,Wen L. Soong. Pulsating torque minimization techniques for permanent magnet AC motor drives - a review[J]. IEEE Trans. Ind. Electron.,1996,43(2):321-330.
[11]石宏顺,夏堃,崔浪浪. 提高电机力矩波动系数测试准确性的优化方法[J]. 机电信息,2020(15):36-37,39.
Research on Torque Ripple of Permanent Magnet AC Torque Motors Under Overload Conditions
YUE Tong1,WEI Guo1,WANG Qian2,YU Xiao1,LEI Han1
( 1.Norla Institute of Technical Physics, Chengdu 610041, China; 2.School of Electrical Engineering and Automation, Harbin Institute of Technology,Harbin 150001, China )
Permanent magnet AC torque motor has the characteristics of high torque density, high control precision, free maintenance. And torque smoothness is one of the key indicators. The paper analyzes the torque ripple of permanent magnet AC torque motors at different load conditions ( including light load, rated load and overload ), and reveals the relationship between torque ripple and saturation. It is shown that the torque ripple is closely related to the load level. As the load increases, both the peak torque ripple and torque ripple coefficient tend to rise first, then fall, and rise again. Electromagnetic torque fluctuation is significantly higher than the overall torque fluctuation, which can only reflect the trend of overall torque fluctuation. The variation trend of load cogging torque peak value is almost the same as that of electromagnetic torque fluctuation, and can also be used as a reference value for judging the overall torque fluctuation.
permanent magnet AC torque motor;overload;torque ripple
TM351
A
10.3969/j.issn.1006-0316.2022.09.003
1006-0316 (2022) 09-0015-09
2021-10-12
岳通(1977-),男,四川南充人,硕士,研究员,主要从事系统总体结构方面的研究工作,E-mail:hityuetong163@163.com。
