基于时空注意力Bi-LSTM模型的短时交通流预测

赵恒辉，黄德启，曾 蓉，於积荣

(新疆大学电气工程学院，新疆 乌鲁木齐830047)

1 引言

随着城市化进程加快以及居民出行量剧增，交通问题也随之突出，交通问题需要智能交通系统的监控和保障。智能交通系统将多种技术结合并运用于庞大的交通运输管理体系，从而对交通运行状况进行合理的调度[1-2]。准确的交通流预测对于道路通行发挥重要的作用，通过对道路交通流的预测，道路监管部门能够及时得到反馈，从而对道路通行进行合理调控。

现有的交通流预测方法[3]可分为基于参数方法、非参数方法和组合模型预测方法。参数模型大多基于经验得到固定结构的模型，主要包括时间序列法、卡尔曼滤波法等。韩超等[4]基于ARIMA模型对时间序列进行实时自适应预测算法。王莹等[5]分析交通流的周期性波动规律，构建了SARIMA预测模型。Kumar S V[6]为克服ARIMA局限性，提出了基于卡尔曼滤波的预测模型。非参数的方法主要包括机器学习和神经网络的方法。傅成红等[7]针对传统回归模型拟合数据能力的不足，提出了基于深度学习回归机预测模型。Liu等[8]针对交通流随机性的特点，研究了K近邻模型的最近邻数对不等时间间隔交通流数据预测性能的影响。组合模型是结合不同模型的特点和优势建立的模型。马秋芳[9]利用改进PSO算法优化BP网络参数后进行交通流预测。Liu等[10]采用K近邻法重构出与当前交通流相似的时间序列，并利用SVR模型进行预测。成云等[11]将差分自回归滑动平均(ARIMA)与小波神经网络(WNN)进行组合预测。Wang等[12]利用贝叶斯方法优化支持向量回归的参数，提出一种BO-SVR结合的预测模型。深度学习[13-14]的发展和不断成熟让越来越多的研究者转向将其应用于交通流预测。Shuai等[15]提出差分进化算法(DE)与长短时记忆网络(LSTM)组合的预测模型。张阳等[16]为克服非稳定交通流状态下预测精度不高，提出一种改进小波包分析和长短时记忆神经网络组合(IWPA-LSTM)的短时交通流预测模型。吕田等[17]提出一种基于SDZ-GRU的多特征交通流预测方法。

上述预测方法仅利用了预测时刻之前的交通流数据，没能进一步挖掘与预测时刻之后交通流数据的联系，并且上述模型也未能充分考虑各个时刻交通流特征对预测时刻的影响程度。因此，本文结合交通流的时空特性，提出了一种将注意力机制[18-19]与双向长短时记忆网络(Bi-LSTM)组合的预测模型，利用Bi-LSTM网络关联历史时刻与将来时刻交通流信息，引入注意力机制计算不同时刻输入的重要性，并通过实时交通数据进行实验，证明该模型预测的准确性。

2 时空注意力Bi-LSTM模型

2.1 LSTM循环神经网络

传统的RNN神经网络在实际应用中存在梯度消失和爆炸问题，为此引入了LSTM循环神经网络，它使用一个记忆模块代替传统循环神经网络的隐藏层节点，相比于RNN网络具有了记忆功能，它由一个储存时间状态的记忆单元以及输入门、遗忘门、输出门三个门控单元组成。其记忆模块各个门控单元在t时刻的计算公式如下

it=σ(wxixt+wsist-1+wcict-1+bi)

(1)

ft=σ(wxfxi+wsfst-1+wcfct-1+bf)

(2)

ot=σ(wxoxt+wsost-1+wcoct-1+bo)

(3)

(4)

(5)

st=ot∘tanh(ct)

(6)

σ(·)为非线性sigmoid激活函数，其数学形式为(7)式；tanh(·)为双曲正切函数，其数学形式为(8)式。

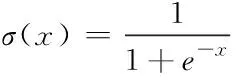
(7)

(8)

2.2 Bi-LSTM循环神经网络

在进行交通流预测时，由于传统的LSTM神经网络只使用了历史时刻的交通流数据信息来预测下一时刻的交通流，没有考虑到预测时刻之后的数据信息，而关联预测时刻前后的交通流变化可以有效提高预测精度。因此，为了引入更多信息，从而对输入数据的表达更加细粒度化，本文选用Bi-LSTM循环神经网络作为基础模型。

Bi-LSTM循环神经网络是两层LSTM网络的叠加，第一层从左侧获取输入并执行前向计算；第二层从右侧获取输入并执行后向计算。在LSTM的基础上，结合输入在两个方向上的交通流信息，对于t时刻输出，前向LSTM具有t时刻及t时刻之前的交通流信息，后向LSTM具有t时刻及t时刻之后的交通流信息，在训练时，模型进行双向预测，最后将得到的两个结果融合作为输出。其模型结构图如图1。

当模型获取输入xt∈n×d时(n为样本数，d为输入个数)，Bi-LSTM网络的前向隐藏状态n×h和后向隐藏状态n×h(h为隐藏单元个数)分别通过LSTM网络由式(9)和式(10)计算而得

(9)

(10)

yt=htwhy+by

(11)

式中：why、by为模型训练的权重参数。

2.3 注意力机制

注意力机制是一种带权池化方法，通过查询(Query)到键(Key)和值(Value)的映射，对具有长期依赖关系的序列实现更强的捕捉能力，并且能够减少网络在训练过程中伴随的信息损失。本文将自注意力机制(Self-attention)引入到Bi-LSTM网络中，通过自注意力机制计算不同时刻交通流输入特征的重要性，继而对输入特征给予不同的权重，突出一些重要特征，从而提高预测准确性，注意力机制的计算公式如下

εt=tanh(Wwht+bw)

(12)

(13)

s=∑tαtht

(14)

其中，Ww，bw，uw是训练模型设置的参数，uw对应于自注意力机制中的Query；εt为t时刻Bi-LSTM模型的隐藏状态ht得到的注意力评分值，其对应于自注意力机制中的Key；αt为每个时间步隐藏状态ht对应的注意力权重系数，隐藏状态ht对应于自注意力机制中的Value；s为最终加权求和得到的特征向量。

2.4 时空注意力Bi-LSTM模型的设计

本文提出融合自注意力机制的Bi-LSTM网络的预测模型，模型结构如图2。该模型包括输入层、两层Bi-LSTM隐藏层、一层Attention层和一层全连接层。经过预处理的交通流二维数据矩阵经过Bi-LSTM的输入层输出到Bi-LSTM隐藏层、经过两层隐藏层中LSTM单元双向计算将结果输入到Attention层，在Attention层，计算Bi-LSTM隐藏层输出作为输入对应的注意力评分，之后进行归一化得到注意力权重，最后将权重与当前输入加权融合输入到全连接层中，计算得到最后的预测值y。

基于时空注意力Bi-LSTM模型实现的整体思路如下：

步骤1：数据预处理。通过插值法拟合缺失值进行填充，剔除异常值，并对数据进行归一化处理。

步骤2：特征提取。将预处理过的交通流数据构建成数据矩阵的形式输入到Bi-LSTM模型中，其Bi-LSTM网络工作如下：

1)设2n个时间步长的交通流序列输入为(xt-n，…，xt，…，xt+n)，将其以不同方向输入到Bi-LSTM模型中。

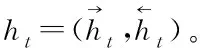
步骤3：特征增强。将Bi-LSTM网络的隐层输出ht输入到自注意力机制层，进行权重分配，之后加权求和输入到全连接层，计算t时刻的输出yt。

步骤4：对输出值yt进行反归一化处理得到真实值。

步骤5：结果对比。将该模型的预测结果与其它模型进行对比分析。

3 实验研究

3.1 数据来源

本文实验使用美国加州开放的PeMs交通数据库公布的数据。该系统将道路的实时信息以30s一次频率向加州大学伯克利分校的计算机工作站发送数据，之后数据经过处理，聚合成时间间隔为5分钟的形式储存在数据库中。

选取的实验路段如图3，该路段包括具有上下游关系的9个检测点，依次是VDS400814、VDS407475、VDS400078、VDS401542、VDS401111、VDS401056、VDS401095、VDS401110和VDS400801，采集到的数据是各检测点在2019年3月1日至3月31日的交通流数据，由于交通流以每5分钟时间间隔聚合，则日交通流量序列共有288个样本，每个VDS在31天共有8298个样本，本文通过训练各检测点前25天的交通流数据，对目标检测点最后一天的交通流进行预测。

3.2 时空数据矩阵

图4为目标检测点及其上下游相邻两个检测点从3月1日到3月8日的交通流数据，从图中交通流的变化规律可以看出，各检测点的交通流在相同时间段的变化具有相似性，表明交通流数据具有时空相关性，因此本文基于交通流的时空特性构建时空数据矩阵。

通过引入目标检测点及相邻检测点交通流数据，构建了一种基于时间维度和空间维度的二维数据矩阵X。定义p个检测点在给定的连续n个时间段的交通流数据矩阵的形式如下

(15)

其中，xi，t-n表示第i个检测点在第(t-n)时刻的交通流，该交通流数据矩阵的每一行表示相同时间段下不同检测点的交通流集合，将各行表示为一个时间序列的形式，根据这些给定的历史时间序列去预测目标检测点在某一时刻的交通流量。

3.3 模型评价标准

本文采用平均绝对误差(Mean Absolute Error，MAE)和均方根误差(Root Mean Square Error，RMSE)来评估模型的有效性。评价指标的值越小，则模型的预测性能越好，其各自的数学表达式为式(16)和式(17)

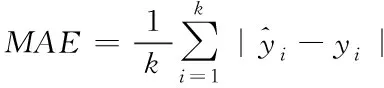
(16)

(17)

3.4 实验结果与分析

本文将滑动窗口数设置为9，即使用9个时间步长的历史数据预测下一时刻的值。经过多次实验，Bi-LSTM网络的参数设置为：输入层数为1，输入层神经元个数为9，隐含层数为2，隐含层神经元个数为24，激励函数选用tanh激活函数，反向传播过程中优化器采用Adam算法，学习率为0.001。为了提高模型的泛化能力，防止过拟合，加入dropout正则化，其参数设置为0.2。选取该路段中间检测点VDS401111在3月31日的交通流量进行分析，预测结果如图5。

图5中，基于时空注意力Bi-LSTM模型的预测结果整体能够较好的拟合交通流的变化趋势，对于某些高峰时段交通流，该模型也能够反映车流的变化规律。实验中使用未引入注意力机制的Bi-LSTM模型与之对比，预测结果如图6，其模型的参数设置与本文建立模型保持一致。图6中，单纯使用Bi-LSTM模型大致能够满足交通流的变化，但是在某些时间段，预测输出偏离真实值，在时间段[100，150]内，预测输出波动较为平缓，对比在时间段150左右和250左右拟合情况可以看出，本文提出的预测方法相对于该模型更好的描述了交通流的变化趋势。

该模型与其它模型预测性能的评价指标结果见表1，由表1可知，基于时空注意力Bi-LSTM模型相比于Bi-LSTM模型，其MAE指标降低了3.80%，RMSE指标降低了2.72%，表明引入注意力机制的可以提高预测精度。

为评估该模型的预测性能，将该模型还与传统LSTM循环神经网络进行对比，其预测结果如图7。其中，LSTM模型参数设置为：隐藏层数为2，隐藏层单元数为24，采用Adam优化算法，学习率为0.001。图7中，基于LSTM模型的预测结果在时间段150左右的交通流预测值普遍低于真实值，没能很好的拟合该时间段交通流的变化规律。同时由表1可知，Bi-LSTM模型相比于LSTM模型，其MAE指标降低了3.82%，RMSE指标降低了1.92%，这表明关联预测时刻前后的交通流数据信息可以更好地反映交通流变化规律。而基于时空注意力Bi-LSTM模型相比于LSTM模型，其MAE指标降低了7.48%，RMSE指标降低了4.61%。综合上述结果表明，本文提出的预测方法在反映交通流的变化规律上优于上述两个模型，证明该预测模型有效提高了预测精度。

表1 模型预测性能比较

同时，本文还选取了传统的BP神经网络模型和SVR模型作对比。其各个模型的预测结果为图8和图9。其中SVR模型采用的核函数为高斯核函数。从拟合情况可以看出，本文提出的方法在预测性能上明显优于传统模型，由表1可知，融合注意力机制的Bi-LSTM相对于SVR模型，其RMSE指标降低了23.87%，MAE指标降低了21.62%，这表明深度学习模型对于提取时间序列的特征效果更好。

4 结论

1)本文利用Bi-LSTM网络的双向计算去挖掘预测时刻前后的交通流变化规律，将自注意力机制引入到模型中，计算不同时刻输入特征的重要程度，形成具有概率分布的特征表示，从而有效提高预测精度。

2)通过使用交通流数据进行仿真，实验结果表明，本文建立的预测模型整体能够较好的拟合实际值，将该模型与未引入注意力机制的Bi-LSTM和单向LSTM相比，其MAE误差指标分别降低3.80%和7.48%；RMSE误差指标分别降低2.72%和4.61%，证明了该模型对交通流预测有较好的预测性能，能够为辅助预测提供良好决策。