基于感染力与免疫作用的新型冠状病毒肺炎疫情传播模型*

刘程芳 梁雨朝 周 健 左永春**罗辽复

（1）内蒙古大学生命科学学院，呼和浩特 010070；2）内蒙古大学省部共建草原家畜生殖调控与繁育国家重点实验室，呼和浩特 010070；3）内蒙古大学物理科学与技术学院，呼和浩特 010021）

1918年的流感被认为是人类历史上最致命的流行病，它感染了当时全球25%以上的人口。在1918年6~7月、1918年9~11月、1919年2~3月 期间，共发生3次大流行，每次流行持续2~3个月［1］。2003年的严重急性呼吸综合征（SARS）也在几个月内来了又去，解释它的来去匆匆对于估计和控制当前的新型冠状病毒肺炎（COVID-19）疫情很重要［2］。

严重急性呼吸综合征冠状病毒2（SARS-CoV-2）属于β冠状病毒属（Betacoronavirus），与严重急性呼吸综合征病毒（SARS-CoV）、中东呼吸综合征病毒（MERS-CoV）同源，相似性分别为79%与50%［3］，通过刺突蛋白（S蛋白）形成的三聚体与人血管紧张素转换酶2（ACE2）受体结合来识别并进入人体细胞［4-5］。SARS-CoV感染人体后具有广泛的临床表现，可使患者出现严重程度不等的各种症状，包括但不限于发烧、咳嗽、味觉丧失等，严重者甚至产生肺炎、多器官衰竭等可致人死亡的重症，具有显著的危害性［6-7］。与SARS-CoV不同的是，自2019年冬天出现以来，COVID-19疫情并未同2003年SARS疫情一样随天气转暖自行退去，而是迅速席卷全球，感染人数超过3亿，严重威胁着人类生命安全，对全球经济造成了严重的破坏。

作为RNA病毒，SARS-CoV-2在传播迅猛的同时，演变出了数种新型突变体。这些突变体往往具有更强的感染能力，使病毒传播更加迅速，或强化其免疫逃逸能力，使疫苗构筑的免疫屏障无法发挥应有的作用，甚至部分毒株同时具备上述所有特性。2020年9月，英国发现新型冠状病毒Alpha变体，该变体具有23个突变位点，关键突变位点N501Y和HV69-70使病毒S蛋白与宿主受体ACE2结合更加紧密，这意味着病毒的传染性大大增强［8］。事实上，Alpha变体在产生后的几个月里迅速肆虐欧洲［9］。值得庆幸的是，有研究表明，Alpha变体并没有显著影响疫苗的防护效果［10-11］。而发现自南非的Beta毒株则有所不同，在与Alpha变体共有N501Y突变位点的同时，其具有K417N/T突变位点［12］，这大大增强了它的免疫逃逸能力。南非的一项研究显示，在疫苗接种者中，阿斯利康疫苗的保护效果平均仅有21.9%［13］，很快，Beta变体在非洲大陆同样流行起来［14］。显然，SARSCoV-2并没有停下突变的脚步，紧随其后的Delta变体，感染能力与免疫逃逸能力兼而有之，正在肆虐的Omicron变体，两种能力更是大幅提升［15］，COVID-19疫情防控形势日益严峻。

COVID-19造成严重破坏需要多长时间？如何及时了解变体，跟上病毒变异的步伐？针对上述问题，已有SARS-CoV-2刺突蛋白构象转变理论给出了病毒感染的机制［16］。同时，认为有必要对传染病的流行和控制进行全面的流行病学研究。

本文提出了基于传染病感染因素及趋势的理论模型，给出了感染和免疫相互制约的定量表述，论证了病毒演化所遵循的免疫加强而感染减弱的一般规律，并提出2个传染病相关参数，感染力参数A、免疫作用参数B。该模型描述了病毒在传播过程中的动态变化与感染-免疫相互作用机制，并用于分析传染终止时间、感染人数与模型的内在联系。通过使用当下疫情数据进行模拟与验证，我们分析了SARS-CoV-2的变异以及变异中上述参数的动态变化，并比较了各突变株的综合传染性。拓展了感染人数与时间的联系，探究了实际中可能出现的变异株混合感染情况。通过成比例消除感染力参数A及免疫作用参数B，并计算观察误差，验证了病毒传染力参数与免疫作用参数只与毒株自身有关，与地域无关。

1 材料与方法

1.1 数据收集与统计

本研究从世界卫生组织官网（WHO）列出的需要关注的变异株（VOC）、需要留意的变异株（VOI）和先前监视下的变异株（VUM）（https://www.who.int/zh/activities/tracking-SARS-CoV-2-variants）中选取10株代表毒株（表1~3），并收集它们主要流行地区的传染情况用于验证分析，各地区具体每日新增感染人数（截至2022年2月25日）来源于世界卫生组织统计数据（https://covid19.who.int/info），各地区传染毒株种类构成及占比情况来源于outbreak.info网站（https://outbreak.info/）。

Table 1 Variants of concern(VOC)

Table 2 Variants of interest(VOI)

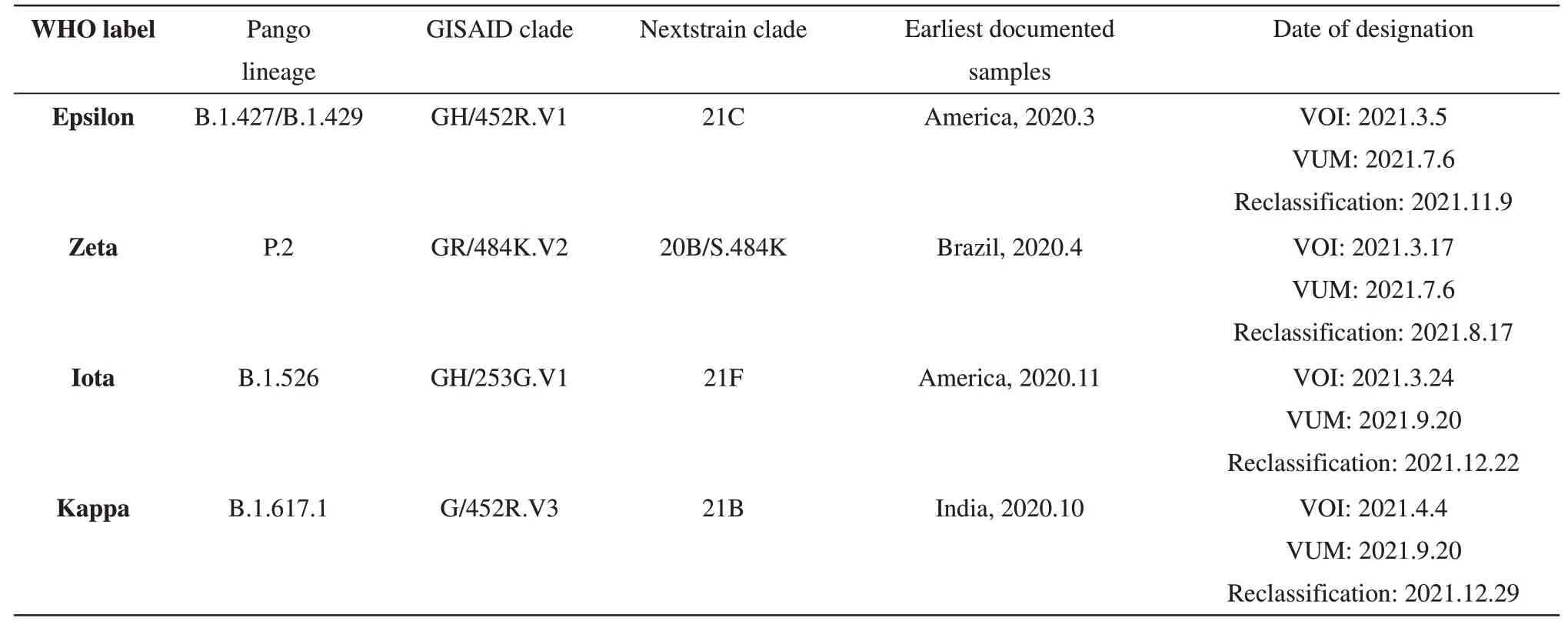
Table 3 Variants under monitoring(VUM)

1.2 基于传染病方格模型的初步研究

传染病方格模型将传染空间视作平面上紧邻的无数方格（图1），最初感染的方格（红色）以步行的方式向四周的方格扩散并占领，即病毒传染。

扩散规则如下：

a.随机选择一个周边空方格（白色）；

b.以概率p1占领之（即感染成功，白方格变为红色）以概率p2+p3禁阻之（即感染失败），p2代表该方格已有免疫力（用绿色表示，即该处白方格标为绿色），p3代表该方格已有隔离措施（用黄色表示，即该处白方格标为黄色）。

假设流行病的传播发生在最近的方格处。在这里，被占用的方格被认为是受感染的，未能占用的方格被认为是免疫感染的（出现概率为p2，即绿色的方格）或采取隔离措施的方格（出现概率为p3，即黄色的方格），而空置的方格（白色的方格）被认为是那些没有受到流行病影响的方格。采取隔离措施的方格是指该方格与其最近方格间的社交距离足够大，这是由于采取了病毒传染的隔离措施，例如使用口罩等［17］。若病毒传播链由n个步骤组成。假设流行病的传播发生在有规律的时间间隔τ，有传染总时间T=nτ，参数n本质上是传播时间（实际可理解为步行次数），参数τ则受毒株种类与地方防疫强度影响。因为通过疫苗等方式具有免疫力的人数随着n增加而增加，所以可以假设p2随着时间n增加，即：

其中，a代表病毒在人群中的初始免疫作用，b代表随时间增长，病毒免疫作用增加的系数，β则代表着时间n的一个调节指数。如果隔离措施的强度是固定的，那么给出常数c代表p3，则p1会随时间减小，根据p1+p2+p3=1，则有：

将上述两个步行规律与公式（1）和（2）结合起来，通过计算机模拟得到一个正方形范围内被占用方格的步行占用情况，利用方格步行来模拟传染病流行，红方格的步行情况即描绘了病毒成功蔓延的情况，每次蔓延成功率是p1。而绿、黄方格则描绘了病毒流行过程中被阻断的情况，它们各自的阻断概率分别为p2、p3，显然，p2+p3代表的就是方格模型中的禁阻格子。如果步行在n的某个阈值停止，则疾病在该阈值n处得到控制。本文的任务就是寻找使步行尽早停止的条件［18-19］。

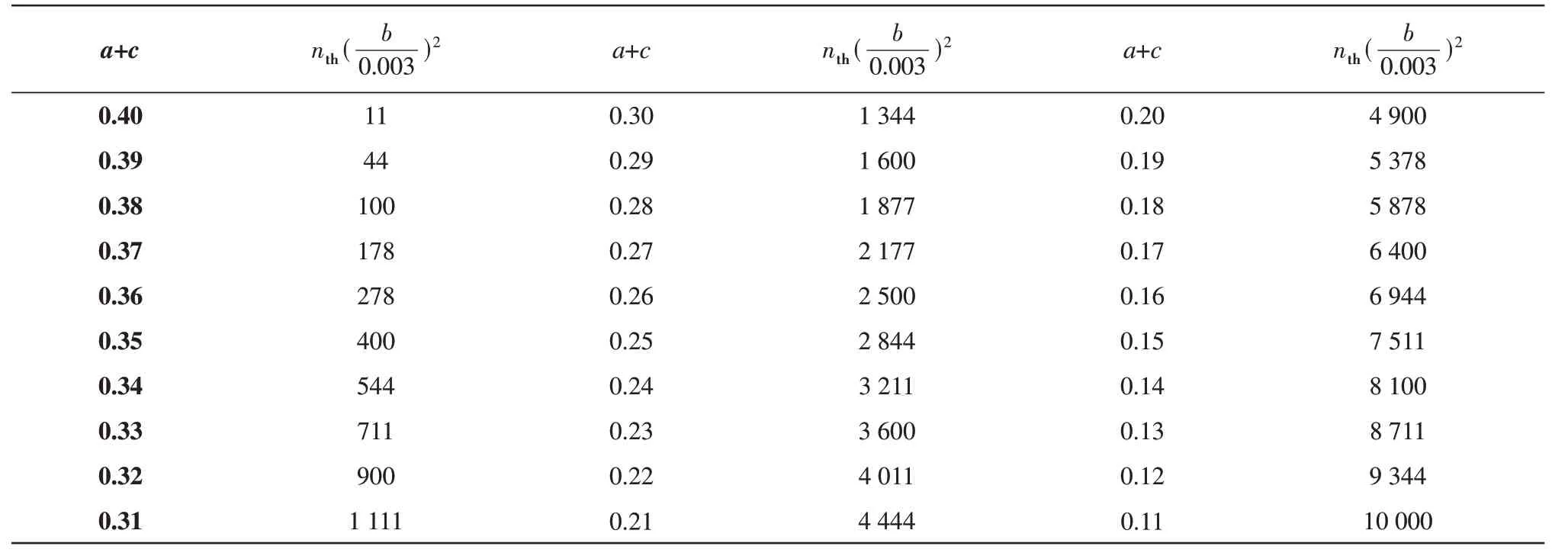
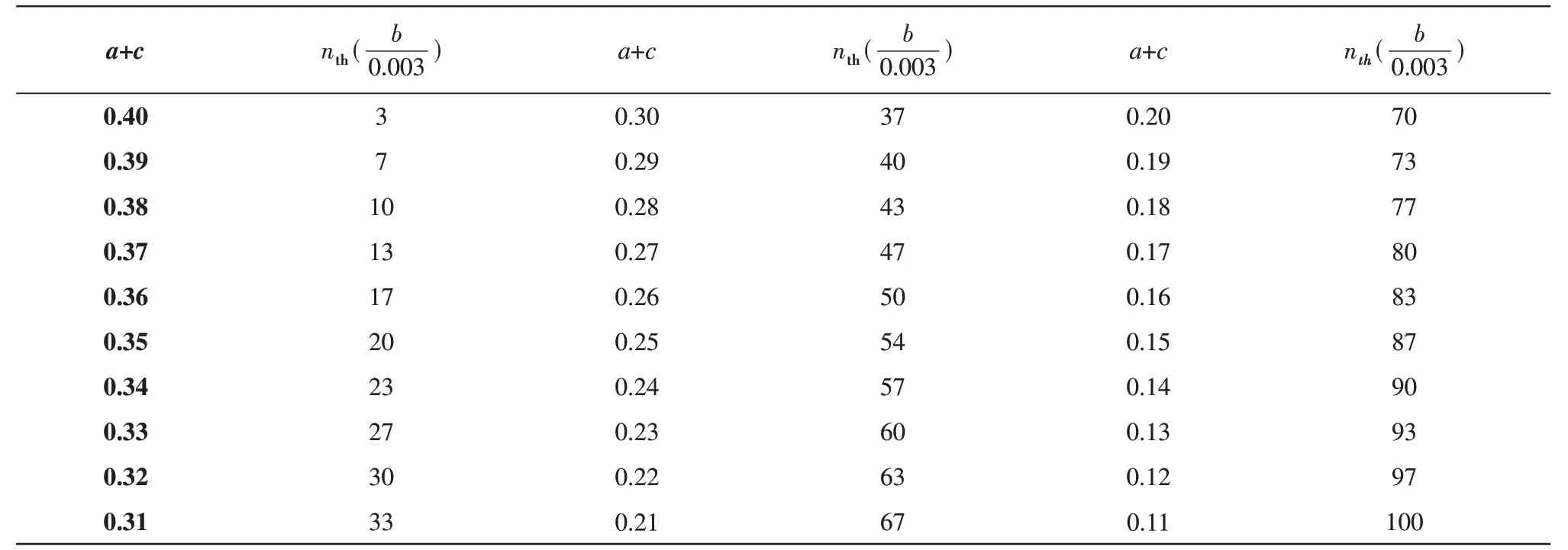
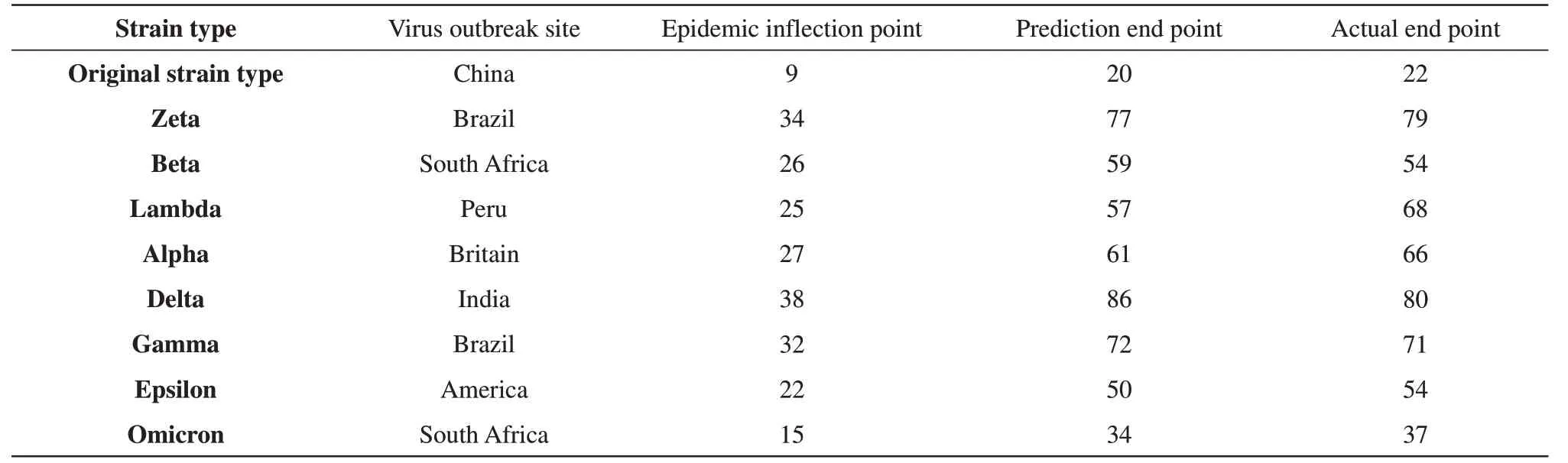
计算机模拟表明，对于p1存在一定的临界值pc。当p1

即当n>nth时，流行病就已经得到了控制。注意，nth与步行时间阈值Tth（感染时间，后实例验证时单位为天）有关，因为文中假设β=1/2，就有：

结合实际流行情况通过网格搜索的方法进行拟合计算，得到了步行次数nth的阈值，用于推知疫情周期的长短，通过和实际情况的对比，证明该模型基本是正确的。也就是说，疾病的流行和控制与免疫作用及隔离措施密切相关，而免疫作用中的参数β取1/2是合理的。从统计理论的角度看，β取1/2和爱因斯坦的扩散理论正相符合［20］。

然而，方格模型显然过于简单，它的紧邻方格传播的观念是过于简化的；它用传播次数来代替传播时间，忽略了τ的可变化性质；它也没有讨论病毒的可变异性。在这样的情况下，引出了病毒传染时间与人数的相对关系并建立了相关普遍理论模型，通过该模型，可以更精确地量化参数，动态地预测每日新增感染人数，还通过模型导出了传染终止时间与疫情拐点之间的关系，可以更便捷地预测传染终止时间。

1.3 感染人数与传染时间关系的普遍理论

在上面的基础上，提出了传染时间与感染人数的相对关系：

令t=nτ时感染人数M（n）遵守方程：

这里A代表感染力，B代表免疫作用。

由公式（5）解得：

解释了M从M0出发随时间增长，当M达到极大，当M又减小至M0。因此传染终止的时间为达到极大时间的9/4倍。公式（6）给出的曲线可以用实验资料进行严格检验。例如在今年2月16日爆发的呼和浩特疫情中，感染人数高峰在月底出现，而传染结束预测在3月中旬，符合预期结果。

公式（6）也可作：

公式（7）为传染天数与感染人数的相对关系式，t即为传染天数，以上为普遍理论。

将普遍理论中的参数与方格模拟的参数对应起来，即A与0.41-a-c有关，B与有关，故传染终止时间为：

A代表着病毒的实际固有感染力，A越大，则病毒的感染能力越强。B表示着群体免疫水平，B越大，则代表群体对此种病毒免疫抵抗能力越强。

现在补充了普遍理论，不仅能求得传染终止时间，还能对传染的日变曲线进行预测，来和实验资料比较。在本模型中，可以根据终止时间在达到疫情极大值点时间9/4倍的理论（公式（6）），便捷地预测疫情终止的时间；也可以通过相同地域不同毒株的感染参数变化来比较各毒株的感染能力；在验证参数A，B只与病毒自身因素相关，与地域因素无关后，还可以通过相同毒株不同地域的τ值来比较各地的防疫水平；最后，在确定毒株在起始地的标准感染参数和各地的防疫水平后，就可以将标准参数拟合为适合该地的参数，并将其代入公式，即使在没有疫情拐点数据的情况下，只要有起始疫情数据，即可进行动态的感染日变曲线预测。

1.4 病毒的突变分析和多毒株混合传染模型

在病毒传播过程中，随着步数n的增加，概率p2增大，p1减小。这意味着如果不发生突变或进行任何治疗，病毒传染的普遍趋势是免疫的增强和感染数的减少。但是，只要传染还没有停止，病毒变异的发生就是不可避免的。

因此，本文选取了多种具有代表性的变异毒株进行突变分析，讨论突变型的氨基酸电性变化对病毒传染力的影响。依据Le Chatelier原理与上述理论分析了突变的方向与理论的参数变化，并给出了相应的防控举措［21］。

随后，收集了各个国家及地区包含多种无变种或变种毒株的传染情况，以爆发曲线的一个完整的涨落作为一个传染周期，收集数据并使用网格搜索的方法拟合模型参数，以平均偏差最小作为拟合依据，以得到实际数据的理论模型参数。

同时，考虑到公式（7）是感染人数与传染时间相对关系的基本公式，它针对了只包含一种毒株的情况，而现实中往往在一个爆发周期中会出现多种变异毒株混合，这时再简单套用单种毒株的研究方法显然是不合理的，并且由于各毒株传染能力的不同，在传染过程中可能会出现各种类毒株占比变化甚至相互替代的情况，这可能会造成爆发曲线的延长甚至双峰的出现。因此，探究多种毒株混合情况下的传染规律是非常必要的。

为此拓展公式（7），使其更适用于多种毒株混合传染的情况：

具体规则如下：

a.i代表毒株种类，通常i只取2个值，即认为爆发曲线中主要占比毒株为两支，其余占比较少毒株可忽略不计；ki为混合比，M0在爆发曲线中的初值，是已知的。

b.在拟合各毒株参数时可参考起始地参数，但应留出τ变化的误差范围，这里设定未知在参考的±0.03范围内拟合，未知±0.003范围内拟合；若没有起始地参数可以参考，则按照原本的拟合规则拟合。

最终通过参数及其组合变化分析了各变异毒株的感染力、免疫逃逸作用、综合传染性；评估了爆发地的隔离措施强度与抗体水平。

1.5 同种毒株A、B是否受地域影响的猜想验证

根据上面的理论可以知道，A和B与病毒自身性质、病毒与人体共存的性质有关。那么A和B是否与地域有关呢？并且，由于τ仅受毒株种类以及当地防疫强度影响，在限定毒株种类的情况下，若A和B与地域无关，那么A和B与τ也将是无关的。这对明确参数意义，探究流行规律具有重要影响。因此采用以下的方法验证：将待验证地的参数与起始地参数相比分别消去A与B，得到两个τ的比值（设起始地的τ为τ1，待验证地的τ为τ2，即得到了两个由于τ之比是定值，那么在一定误差范围内，若两个相等，则可以说明假设成立。

2 结果与讨论

2.1 nth的阈值计算

nth的阈值计算结果如表4~6所示，结果趋势如图2所示。计算表明，a+c≥0.41时，疫情已经得到控制，如果传播时间足够长，那么疫情总是可以控制的（公式（4））。β取1/2是由于随机步行的距离与步行时间的平方根成正比［22］。从表4~6与图2中很容易发现，在β分别取1/4、1/2、1的3种情况下，结果相差很大，其中β取1/4时千万量级的步行次数与β取1时十位量级的步行次数均不符合实际情况，而β取1/2时，千位量级的步行次数与波动范围则较为符合实际，这也说明了β取1/2的合理性。而对于给定的b，阈值nth会随着参数a+c的减小而迅速增加。这意味着加强病毒隔离和增加社交距离（例如增加c值）是控制流行病的重要途径。相反，强度较弱的社会隔离需要更长的时间才能消除传染病。上述论点与参数b的选择无关，因为b2和nth在理论中是协调调节的。表5给出的阈值估计值可用于分析2003年SARS-CoV和目前SARS-CoV-2在世界不同地区的流行和控制情况。

Table 4 Threshold of the number of walks nth(β=1/4)

Table 5 Threshold of the number of walks nth(β=1/2)

Table 6 Threshold of the number of walks nth(β=1)

2.2 传染终止时间的估计

根据理论模型可以简便地估计出疫情中传染终止的时间。这里的传染终止指感染人数回落至疫情爆发起点，预测与实际对照结果如表7所示。

Table 7 Estimated and actual control of infection termination time(d)

2.3 病毒突变的电性与参数变化分析

本文从各处收集了SARS-CoV-2的部分突变及这些突变包含的位点电性变化、感染力变化及免疫逃逸能力变化，希望探寻病毒突变位点的电性与病毒感染力、免疫逃逸能力之间的关系，其具体情况见表8。

Table 8 Partial mutation of SARS-CoV-2

病毒S蛋白上的氨基酸突变列于第4列。表中O表示中性，P表示正电性，N表示负电性。当突变中氨基酸的电性有变化，感染性就强，否则就弱。这是因为电性变化导致S蛋白的结构弹性改变［16］。

免疫逃逸与特定的突变如K417N、K417T、E484K和P681H等有关，它依赖于不完全免疫（免疫力低下）人群的存在。不适当的医疗也会帮助免疫逃逸。Le Chatelier原理指出，如果在平衡状态下对反应施加应力，则平衡将向释放应力的方向移动。由于药物治疗可以看作是一种施加压力，其倾向于增加免疫并降低传染性，则药物治疗下的动态平衡将向相反方向移动。也就是说，突变已经发生，与野生型相比，突变体对中和抗体的敏感性降低，病毒感染性更高。这个现象已在最近治疗免疫抑制个体的SARS-CoV-2突变病毒（刺突蛋白中的D796H和ΔH69/ΔV70）的慢性感染过程中被观察到［23］。免疫逃逸突变一旦被自然选择通过，就会产生新一轮疫情。免疫逃逸突变的形成是COVID-19大流行中出现那么多变异的最重要机制［24］。

2.4 变异毒株的感染力群体免疫响应和危害性

本文对无多种变异毒株混合的情况进行了参数拟合，其中各地区具体每日新增感染人数来源于世界卫生组织统计数据，参数拟合情况见表9。

这些参数能帮助人们在疫情传播曲线上简便地发现各毒株种类的固有感染力与群体免疫水平，便于这些变异毒株得到合理的重视与评估。以南非Omicron疫情举例，Omicron作为目前世界最为流行的突变种，一经出现便传播迅猛，席卷全球［15］。与疫情初期因准备不充足而传播迅速的中国无变种疫情相比，南非Omicron的显著大于原种，这意味着Omicron具有超强的感染力，而却并不如般较原种显著增长，一般来说，感染力的增长会使传染更加迅速，缩短传染需要的时间，τ随之减小，而现在没有急剧增大，说明Omicron的B较原种显著减小，这意味着易感人群对Omicron的免疫响应更为迟钝，Omicron可能进化出了更强的免疫逃逸能力。与其他突变种的对比也是类似，由于Omicron强大的感染能力显著提高，而则由于Omicron强大的免疫逃逸能力导致的B减小一定程度上抵消了传染速度加快导致的τ减小，增长的相对较少。各混合毒株爆发曲线得到最优拟合参数见表10。

Table 9 Parameters of variant strains without mixed cases

Table 10 Parameters of mixed variant strains

这些数据便于对一些更复杂的传染情况进行解释。如美国2020年11月产生的变异曲线（图3），在2021年4月感染人数几乎回落到爆发前的状态时，紧接着产生了一次反弹（5月），形成了一个双峰，这显然不是两个独立的单峰，因为根据第2个峰最终的位置来看，第1个峰的下降位置还远远未到谷底，综合美国的传染情况及毒株占比情况来看，前一个峰是由Epsilon变异株造成的，它是美国的本土变异株，而在它的传染后期，新传入的Alpha变异株与本土新变异株Iota出现在美国，它们的感染能力显然更强，竞争取代了Epsilon成为了主要毒株种，并引起了新一轮疫情的反弹［25］。疫情后期τ增大，Epsilon毒株引起的新增感染人数逐渐减少，而Alpha与Iota的混合传染在这样大的τ下引起了疫情感染人数反弹，也说明了这两者感染能力较Epsilon更强。

以上比较了同种毒株在不同地区感染参数的变化，也就是隔离措施、群体免疫水平对病毒传染速率的影响，也可以用这些参数比较各变异毒株的综合传染性，依据表9、10的结果，将参数消去τ，就可以得到表示病毒株在人群中的综合传染性的参数综合传染性是指病毒对易感人群传染速率与感染成功率的综合评价参数，病毒的感染能力愈强，群体免疫水平愈低，综合传染性就愈高。这里采用变异毒株起始地的参数作为该种毒株参数的代表，其统计数据如表11所示。

考虑到资金、物流、服务支持能力及顾客需求等诸多因素，大部分家电企业的产品并不会直接售卖给终端消费者，而是通过经销商中转到消费者手中。因此，对于以经销商作为开拓、维护市场主力的家电企业来说，经销商管理无疑就成为公司管理中极为重要的一部分。本文以B公司为例，来谈谈家电企业的经销商管理问题及优化方案，希望给读者带来启示。

Table 11 Comparison of parameters of various epidemic strains

根据表11的计算结果，大致可以将各毒株的综合传染性按照从大到小的顺序排列起来，依次为Omicron>Delta>Alpha=Beta>Lambda=Gamma>Kappa>Zeta>Epsilon>Original strain type。理论规律与实际情况拟合的比较好。可以看到，中国最开始的无变种都很高，但毒株综合传染性却很低，这显然是由于疫情爆发初期政府没有准备，隔离措施不完备，免疫水平低造成的τ很小。这与客观事实是比较相符的，实际上，在加大了隔离力度后，中国的疫情得到了显著的、快速的遏制，也有效避免了本土毒株的进一步变异造成的疫情反弹。而将之前最广为流行的两变种Delta与Alpha相比可以看到，二者的综合传染性参数都很高，这也是它们如此流行的原因之一，而Delta较Alpha的更高，这意味着Delta的感染能力更强，感染的条件更低，传染的速率更快；更低，这意味着Delta的免疫逃逸能力更强，疫苗效用更低。这些也是Delta在某些地区取代了Alpha作为优势变种，并引起了新一轮流行的重要原因。

新型变种Omicron目前综合传染性最高，并且相对来说τ也较小，这或许是由于当地的防疫措施未能及时适应新变种的高感染力与高免疫逃逸能力导致的，同时，高感染人数带来的医疗资源捉襟见肘可能使得感染人员无法得到及时的检测与救助，为传染创造了条件。当然，由于感染人数具有不确定性，可能会造成误差，例如表中Beta与Alpha的参数相同，但根据实验数据来看，Alpha的感染能力更强，而Beta的免疫逃逸能力更强，因此需要根据其他感染地区的情况，更为全面的评估突变毒株。

一般来说，病毒的变异会使当前模型中的参数值发生变化［26］。本模型中病毒变异产生的有害作用表现为：a.病毒的变异可能会导致其传染性的增强，这将直接导致A值的增大；b.病毒的变异可能会导致其受机体免疫作用的降低，这将显著降低B值；c.这两种变异在隔离水平保持不变的情况下均会加快传染速率，降低感染一次所需的时间τ，增加感染人数，延长疫情终止的时间Tth，使得疫情更难控制，周期更加漫长。

2.5 同种毒株A、B不受地域变化影响

在前面上述诸项研究的基础上，还发现同种毒株在不同地域流行时，参数A，B保持不变。检验过程见表12。其中每种毒株的第一行即为起始爆发地疫情，其参数作为参考参数，τ设为τ1，其余行为其他爆发地疫情，其参数作为待验证参数，τ设为τ2，与参考参数相比进行验证。

Table 12 Verification that the parameters A and B of the same strain are not affected by regional changes

根据表12的结果来看，绝大部分τ2/τ1比值的差值绝对值都是很小的，这说明两种方式得到的τ2/τ1差别不大，每一地区有一个固定的τ，地区的差别完全表现在τ的差别上，因而A、B与地域无关。当然，由于各地区疫情毒株组成并不唯一，可能混杂了少部分其他毒株，是误差的主要来源之一。例如，在美国Alpha疫情流行过程中，得出的差值绝对值0.34可以在图3的混合感染情况中得到解释。

目前已知同种毒株在不同地区的A、B相同，那么在排除病毒感染因素后，就可以通过同种毒株在不同地区流行情况中τ的水平来评估地方的防疫状态（表12）。如原种流行区域中的中国、美国与英国，显然疫情起始国中国的τ值更小，这是由于疫情初期，人们对病毒认识不足，防疫水平低，且没有有效疫苗造成的。而美国较英国τ值更小，则可能和当时美国防疫政策放松、美国选举、抗议游行等相关，各国τ值在这里的对比鲜明地反映了各地的防疫状态，与实际情况拟合的较好。再如Delta流行区域中的泰国，τ值显著高于起始地印度，说明其隔离措施较好或疫苗普及度更高；而法国τ值则显然低于印度，这或许与复工复产、集会等带来的感染风险提高有关。

3 结 论

本文依据传染病传播的方格步行模型研究了感染持续时间和群体免疫作用的关系。在此基础上提出感染力参数A、免疫作用参数B两个参数，给出了传染时间与感染人数的关系，可以对感染日变曲线进行预测。还分析了SARS-CoV-2的突变，提出氨基酸突变产生的电性变化导致了毒株感染力的变化。文中还引入了突变株综合传染性参数定量比较了各突变株的综合传染性，得出综合传染性排行Omicron>Delta>Alpha=Beta>Lambda=Gamma>Kappa>Zeta>Epsilon>Original strain type。还论证了病毒感染能力和群体免疫作用只与病毒自身性质、病毒与人体共存的性质相关，而与单次传播时间无关，也与这一突变型在何地域传播无关。

在Omicron变种席卷全球，国内疫情形势严峻的当下，本文提出的传染病传播模型可以根据毒株种类与防疫情况，动态地对不同地区每波疫情的持续时间与感染人数做出较精准的预测，便于当地评估疫情严重程度及调整防疫状态。同时，该模型可以根据疫情快速评估各变种的综合传染性，对新变种的出现具有评估预警作用。

面对病毒变异带来的严峻防疫形势，本文根据模型中可能的参数变化给出以下建议：

a.增加疫苗接种的人数，可以提高B值，降低A值，抵消病毒变异引起的A值升高和B值降低。

b.严格隔离措施，阻断传播途径，增大τ值，可以有效抵消A值的升高与B值的降低。

c.对免疫力低下人群的医疗必须谨慎，以减少免疫逃逸为病毒变异提供机会。

同样，本文也存在一些不足，例如未考虑介质传递病毒导致疫情传播的情况，以及疫情数据采集不准确、不及时对评估结果会造成一定影响等。之后的工作将针对这些情况继续优化模型，以获得更精确的预测结果。