重视审题过程 培养思维品质
2022-10-25陈宣新
陈宣新
(浙江省龙游县第二高级中学,324400)
准确解题的前提条件是能够认真审题,正确地理解题意,而要想正确全面地理解所要解答的试题的题意,就需要会审题,就需要在审题的时候能够发现试题所要考查的知识点,全面深入地挖掘出试题中隐藏的解题信息,排除干扰因素,找到解题所需要的突破口.本文结合试题介绍几种审题方法,以有效培养学生的数学思维品质.
一、咬文嚼字,培养思维的缜密性
审题中思维的缜密性,是指学生能够准确理解问题中已给的条件和结论,并能够根据所解问题的要求,排除干扰信息,确定解题方向,找到解决问题所需要的数学知识.
例1已知集合M={x|x-a=0},N={x|ax-1=0},若M∩N=N,则实数a等于( )
(A)1 (B)-1
(C)1或-1 (D)1或-1,或0
分析根据已知条件可知,正确理解M∩N=N是正确解答本题的前提条件,需特别注意N=∅的情况.通过对各选择项的考察,a=1,a=-1都符合题意,主要需考察a=0的情形.当a=0,N=∅,M≠∅,显然有N⊂M,即M∩N=N成立,则应选(D).

分析经审题可知,“对任意的实数x,总有f(x1)≤f(x)≤f(x2)”中,含有不等式恒成立的结论,进而可知x1,x2分别是函数的最小值与最大值点的横坐标,于是|x1-x2|的最小值为函数的半个周期长,所以|x1-x2|的最小值为2.这里准确理解题目中的条件对应于正弦函数图象的意义,就能解决问题.
二、关注结构,培养思维的敏捷性
审题中思维的敏捷性,是指需要学生能够在面对所要解决的数学问题时,快速正确地读懂题目要求,根据已知条件推断出解题所需要的数学知识,准确有效地找到解答问题的关键.这就需要在审题时做到快速、准确、有效.
例3已知在∆ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos 2C=0,求角A,B,C的大小.
分析这是一道与三角形有关的三角问题.在∆ABC中,首先想到内角和定理,即A+B+C=180°,由于sinA(sinB+cosB)-sinC=0,即sinA(sinB+cosB)-sin(A+B)=0,展开整理得sinB(sinA-cosA)=0.又B∈(0,180°),所以sinB≠0,从而cosA=sinA;由A∈(0,180°),得A=45°,则B+C=135°①.又由sinB+cos 2C=0,得sinB=-cos 2C=sin(270°-2C),则B=270°-2C或B=2C-90°,即B+2C=270°或2C-B=90°②.由B+C=135°知B+2C=270°不合,由① ② 联立得C=75°,B=60°.
解题过程就是将已知条件不断向解题目标转化的过程.为了减少失误,优化解题过程,就需要在解题过程中不断审题,不断进行选择判断,明确解题方向.在本题求解过程中对题目的两个关键表达式进行化简,转化有了明确的方向,使整个解题过程顺利进行.
三、分析因果,培养思维的抽象性
审题中思维的抽象性,是指对问题中所给的各种信息进行提炼、浓缩和概括,在审题过程中及时地将其中部分条件进行整理、归类,迅速转化为新的、对解题有用的结论,为后续的解题明确方向,使整个解题过程通畅无阻.

很多情况下,第(1)问的分析过程对解决第(2)问有很大的启发性,在进行第(2)问审题时,如何注意研究这一点是很重要的,也是必须的,当然不是普遍的,也可能有意外的情况出现.
四、挖掘隐含,培养思维的深刻性
审题中思维的深刻性,是指需要学生能够根据所给出的条件,深入理解题目要求,并能从表面的文字叙述和符号表达中找到隐藏的解题条件,即通过现象发现问题的本质,及时地避免误判,跳出解题的误区.
例5设a>0,b>0,方程x2+ax+2b=0与x2+2bx+a=0都有实根,求2a+b的最小值.
分析本题的条件是二方程都有实根,则有Δ1=a2-8b≥0,Δ2=4b2-4a≥0,即8b≤a2与b2≥a同时成立.从代数形式考虑,一时难以下手,如果再进行一次审题,就可以挖掘它的几何意义.联想到两个不等式同时成立所满足几何条件,由于a>0,b>0, 且8b≤a2且b2≥a表示直角坐标aOb内阴影部分的区域(如图1),两条曲线的交点是P(4,2).设t=2a+b,则直线2a+b-t=0与阴影部分有公共点,平移直线,当直线过点P(4,2)时,截距t最小值,将P(4,2)代入,得t=10,即2a+b的最小值为10.

在思路受阻时,通过及时的再审题,挖掘题目其它方面的信息,可能会眼前一亮,新的解题思路就会出现.所以换一个方向,转一个角度,前途就可能是一片光明.
五、多向分析,培养思维的广阔性
审题中思维的广阔性,是指通过精细研读题目,发挥丰富的想象力,从多角度、多方向、多层次去认识问题,分析问题.在审题阶段,要考虑到一个式子、一段表述,可能对应问题的不同表征,如果从不同侧面去理解,就可能得到多种解题思路.

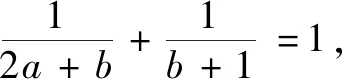

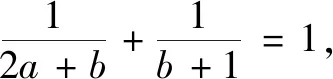
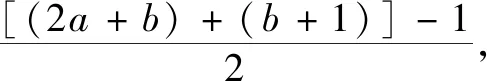
由上可知在审题中,如果将侧重点放在不同的地方,就可能有不同的解题方法.如果在平时学习中,学会从多方面思考问题,然后设法用多种方法解决问题,对思维的广阔性的养成会有很大帮助,同时对学习数学的兴趣提高和思维能力的提升很有益处.
六、放眼全局,培养思维的独创性
审题中思维的独创性,是指让学生在审题时能够根据所掌握的数学知识,发现新的、有创造性的解题思路,并能跳出命题人在试题中给出的某些细枝末节,从全局思考问题,整体思考,综合理解,然后用整体列式、整体运算的方法解决问题.
例7设a,b,A,B均为已知实数,且对任何实数x,不等式Acos 2x+Bsin 2x+acosx+bsinx≤1成立,求证:a2+b2≤2,A2+B2≤1.

从一个式子变化中,要得出两个不同的结论,只有通过不同的变换才能够达到,所以整体思维,整体变换是较好的解题办法,也可能是一种独创的思维结果.
在平时的解题教学中,应该让学生知道审题的重要性,只有严格把好审题这一关,才能在解题中抓住本质,应对自如.
