基于LSTM的热力站短期热负荷预测研究

张腾达，李 琦，陈 波

(内蒙古科技大学信息工程学院，内蒙古 包头 014010)

1 引言

区域供热系统(District Heating System，DHS)的目标是利用局部热源通过管道分布向建筑物供应热量。由于我国北方地区的气候原因，供热面积巨大，因此改善区域供热系统的运行对于节约能源有着重要意义。在热负荷预测中，按照预测周期时间的长短，可分为超短期热负荷预测、短期负荷预测、中期负荷预测以及长期负荷预测，其中短期热负荷预测的目的是使供热量与需求量相匹配。

由于区域供热系统自身具有非线性、大滞后、多变量、强耦合的特点，随着硬件能力的提升和机器学习的快速发展，为热负荷预测的发展带来了新契机。Fang等分析了芬兰第二大城市埃斯波的热需求和室外温度对热负荷预测的影响，并且结合线性回归的SARIMA模型对热负荷进行短期预测，获得较高的精度，但不足的是该模型需要大量连续且充分的历史数据。Zhao等提出一种负荷预测模糊控制策略，对空调系统进行前馈模糊控制，这种控制方法被认为是在保证室内舒适性的同时降低能耗的有效方法，以天津大学某地源热泵系统为例，验证了该控制策略的有效性。但是疏忽了控制过程中由于时滞原因导致的参数变化因素。王琎等提出一种基于DWT和特征选择的热负荷预测模型，与单一ETR和DNN 模型相比更能充分提取数据的非线性特征并且获得更高的精度。姜平等利用T-S模糊神经网络建立热负荷的预测模型预测第二天的热负荷，证明算法具有较好的拟合效果，由于训练数据为过去48小时的144组数据，因此还需要大量数据检验其有效性。Izadyar N等提出了极限学习机的方法，并评估了人工神经网络和遗传编程的算法，得到极限学习机算法在区域供热系统中热负荷预测的优越性。李琦等在传统的BP神经网络基础上采用改进的BP算法得到未来24小时的热负荷预测值。刘鹏飞等通过灰色关联法对影响热负荷预测的因素做了相关性分析，得到影响热负荷相关性最大的因素是供回水温度、供水流量和室外温度，同时选取一个月的数据采用灰色神经网络模型预测热负荷。近年来，由于深度学习的发展，神经网络在其它方面也有长足的发展，孙海蓉等将改进的深度信念网络(DBN)模型和支撑向量机回归(SVR)模型相结合用来预测电力负荷，通过实际数据仿真证明其是一种有效的预测方法。孙瑞奇对LSTM模型进行了模型结构和算法的改进，挖掘出股票价格时间序列中的隐含规律，对股票价格实现短期预测。

基于以上研究内容，结合LSTM神经网络精度高、有效克服“维数灾”和泛化能力强的优点，首先收集整理一年供暖周期大量真实历史数据，对数据进行归一化处理，然后将室外温度作为影响热负荷变化的核心因素，将室外温度序列和热负荷序列之间的非线性关系进行LSTM建模，充分发现数据之间的客观规律，为防止过拟合，在LSTM模型的隐层加入DropoutWrapper函数来提高模型的性能。此外，加入风力因素作为模型的输入，与上述模型分别进行未来24小时热负荷预测实验，同时与支持向量机的3种不同核函数方法进行对比实验，最后，验证LSTM模型对处理时间序列问题的可行性和优越性。

2 区域供热系统理论基础

2.1 区域供热系统原理

区域性供热系统由热源、热力站、热用户以及连接它们之间的管网构成。各部分之间装有循环泵、过滤器、电动阀等各类测量仪表，形成了一个结构复杂的非线性控制系统。为了满足不同区域热用户的供热量，热力站对不同区域热用户供热量的需求对应不同的供给量。如图1所示为区域供热系统原理图，其中由热电厂与热力站构成的为一次侧，经热力站分配给热用户热量之间构成二次侧，热电厂将生产的热量通过换热器和水泵机组将热量由一次侧管网输送到热力站，热力站再经二次侧管网将热量供给到热用户群。针对热用户热量需求和热量供给不平衡问题，本文对热负荷预测采用不同方法进行介绍。

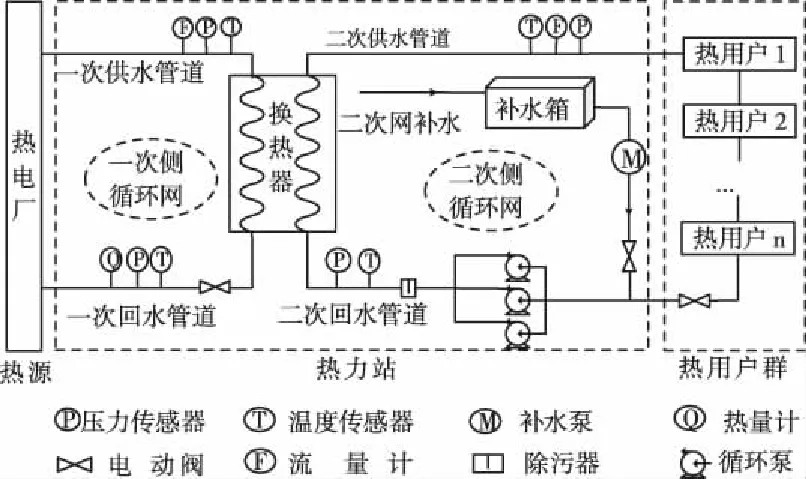
图1 区域供热系统原理图

2.2 LSTM算法原理

LSTM算法来源于循环神经网络(Recurrent Neural Network，RNN)，由于RNN激活函数为tanh，在反向传播更新上一时刻参数的时候，若参数W初始化为小于1的数时，就会出现梯度消失的现象，只能具有短期记忆，鉴于此LSTM神经网络利用门控单元将长、短期记忆结合起来，解决了梯度消失的难题。

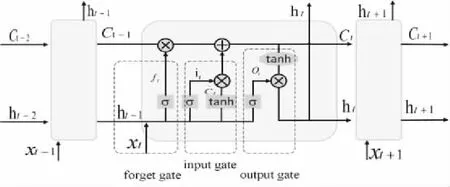
图2 LSTM神经网络结构图

LSTM网络结构图如图2所示，该模型神经网络由3个“门”组成：遗忘门、输入门和输出门，更新过程如式(1)-式(6)所示。

=([-1，]+)

(1)

=([-1，]+)

(2)

(3)

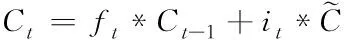
(4)

=([-1，]+)

(5)

=*tanh()

(6)

式中：和tanh 为激活函数，、、、和、、、分别是3个“门”对应相关的权重矩阵和偏置向量。在LSTM神经网络更新过程中，输入门是决定要将哪些信息更新到新细胞中，遗忘门是将和-1作为输入，经过sigmoid函数再与上一时刻-1作乘积以决定哪些信息保留，最后输出门根据输出概率值得到输出预测值。

总之，LSTM神经网络通过“门”来选择需要的信息，区别于传统的神经网络，通过sigmoid和tanh激活函数，使网络降低了梯度消失和梯度爆炸问题出现的可能性，除此之外，LSTM神经网络的优势在于可以依据当前时刻的数据对下一时刻数据产生影响，同时挖掘到数据之间的关系，更适合处理基于时间序列的热负荷预测问题。

3 热负荷预测

热负荷的预测是保障供热系统“按需供热”和热用户舒适安全的基础，供热系统本身的特点有三个：1、室外天气因素方面：气温、光照强度、风速、空气湿度以及紫外线强度，其中温度是最大的影响因素；2、热力公司方面：管网压力、温度和供热流量等；3、非线性、时滞性、以及不同人群不同的生活方式，都会对热负荷预测带来一定的影响，因此，选取合适的热负荷预测方案，建立恰当的热负荷预测模型对于现场控制具有指导性意义。对于热负荷预测的流程，首先通过热力公司提供的历史工况数据，对数据进行预处理，由于区域供热系统具有明显的时间序列特征，LSTM神经网络对于时间序列的问题有独特的优势，因此选择该模型并利用Python语言在Tensorflow库下进行编程，同时对网络参数不断进行优化改进，预测下一时刻的热负荷值，最终循环迭代预测下一天的24小时热负荷序列。

3.1 热负荷数据预处理

本文数据来源于包头某热力公司的历史供热数据，由于数据在采集和存储的时候难免会因为环境或者人为、硬件和软件等因素存在不符合常规的数据，比如温度短时间的骤变和数据的缺失等，LSTM神经网络模型对于数据集的完整性和冗余性以及相关性都有一定要求，因此，干净、简洁有效的数据是模型对于发现数据之间客观规律的重要保障。在整理数据过程中，天气数据来源于中国天气网，其准确性和可靠性较高，常用的离群点分析方法有简单统计量分析：取数据的最大值和最小值范围内的数据，范围之外的数据称为异常值；3σ原则：一组测定值中与平均值的偏差超过3倍标准差的值；箱线图分析等。本文首先采用3σ原则发现异常值，由于前后时间差为1小时，所以利用前后各2个时间点数据的平均值作为该异常值的替代值，如图3所示为热负荷原始数据和处理之后的对比图。

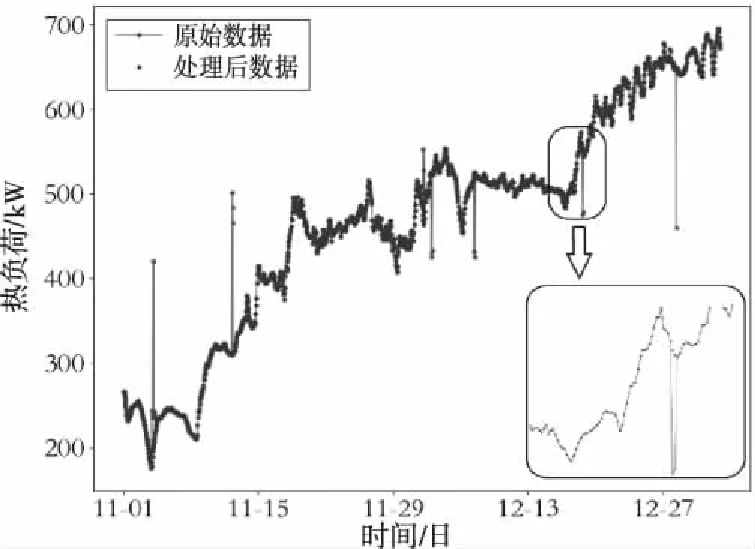
图3 数据处理前后对比图

3.2 LSTM 热负荷预测模型

如图4所示为热力站热负荷预测模型结构图，由于室外温度会影响热水在管网中传递时的热量，因此室外温度和热负荷都在时间序列上对下一时刻的热负荷会产生影响，将历史的热量值和与其对应的历史温度，以及未来时刻的温度值作为神经网络的输入，预测未来时刻的热负荷。模型数据以 24 小时为一个周期，输入数据格式分别为batch＿size：24，time＿step：1，input＿size：3，三个输入变量分别为历史室外温度、热负荷值和未来时刻室外温度，每次训练结束输出一个输出变量，为避免过拟合现象，在模型的隐层加入DropoutWrapper函数，当网络中每个单元在每次有数据输入时，都以一定的概率正常输出，其它输出为0。利用这种有效的正则化的方式，可以有效的防止过拟合，提高模型的性能，达到热负荷预测的目标。

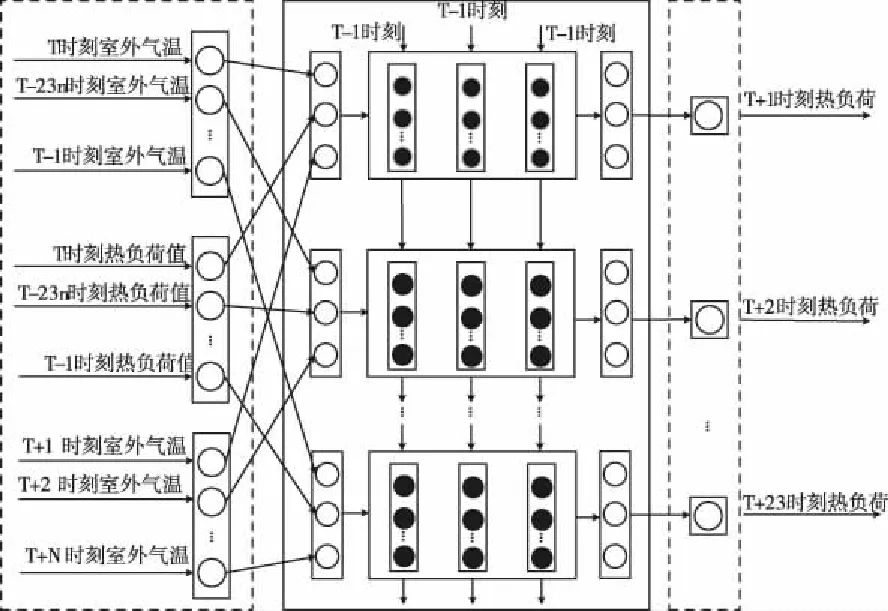
图4 LSTM 的热负荷预测模型

3.3 仿真与验证

本次数据选用包头市热力公司2019年11月份至2020年2月份的供暖时间采集的数据，室外温度数据来源于中国天气网，每1小时采集一组数据，每天采集24组数据，共计采集120天的历史数据，累计收集数据2880组数据，其中把最后一天的24组数据作为验证集，用来验证模型的泛化能力，剩余2856组数据按照4：1的比例分为训练集和测试集。经处理后的数据如表1所示，根据多次预测比对试验隐藏层设置为3层，节点个数为8，学习率为0.0002，循环迭代2000次时，预测效果最好，如图5和图6所示为经LSTM神经网络训练之后验证未来24小时热力站1的相对误差和热负荷预测结果。

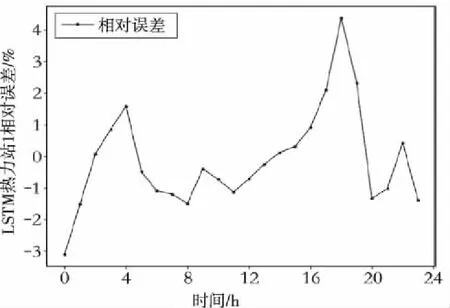
图5 热力站1热负荷预测相对误差

表1 热负荷预测数据

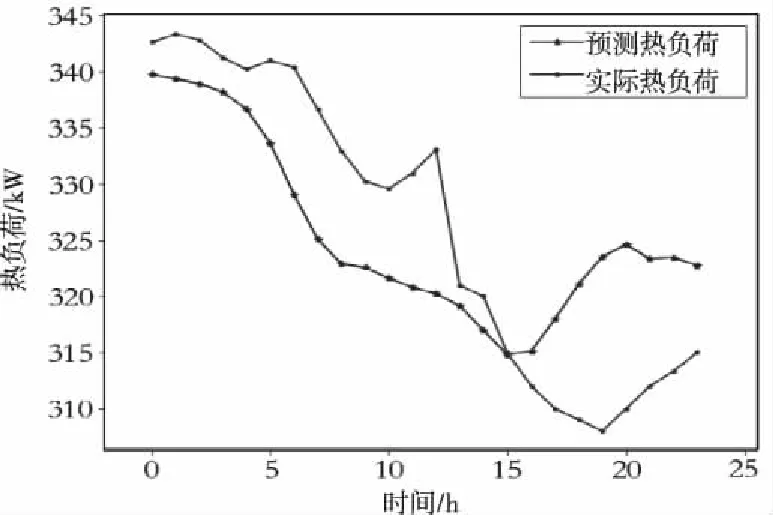
图6 热力站1热负荷预测结果

为了验证模型的泛化能力，另挑选同样时间段的热力站2作为实验对象，在相同实验环境下进行实验，其相对误差和预测结果如图7和8所示。

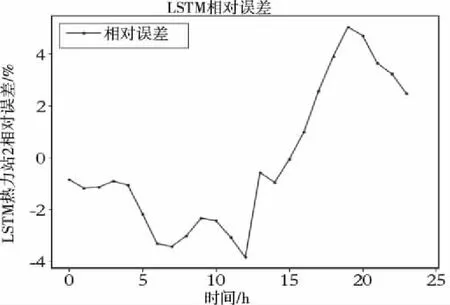
图7 热力站2热负荷预测相对误差

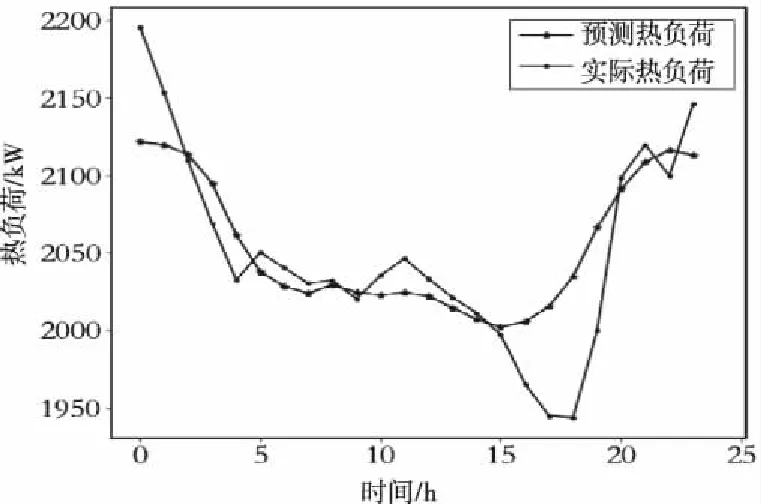
图8 热力站2热负荷预测结果

经过两组实验分析，热力站1和热力站2的最大相对误差分别为4.4%和5.01%，平均相对误差分别为1.24%和2.35%。可以发现，热力站1的热负荷值相比热力站2要大一个数量级，这是因为不同热力站在实际工况中会对应不同规模的热用户群体。基于LSTM的热负荷预测模型误差较小，基本满足目标函数的需求。

除了室外温度是影响热负荷值的第一大因素外，风力因素也是一个重要的直接影响因素，在实际生活中，当上一时刻和下一时刻的检测温度相同的情况下，也有可能热需求是大小不同的，因为较强的风速会导致热需求的增加，特别是建筑物的老化程度不同也会使得热负荷发生变化，所以在输入端加入了风力因素，这样对于基于时间序列的预测模型提供了一个约束条件，有利于模型精度的提高。因此，本文将风力因素作为一个新的输入因素，对热力站1和热力站2在相同参数下实验。如图9-12所示为热力站在有风力因素和无风、力因素的情况下的相对误差和热负荷预测结果图。

图9 热力站1有无风力因素相对误差对比图

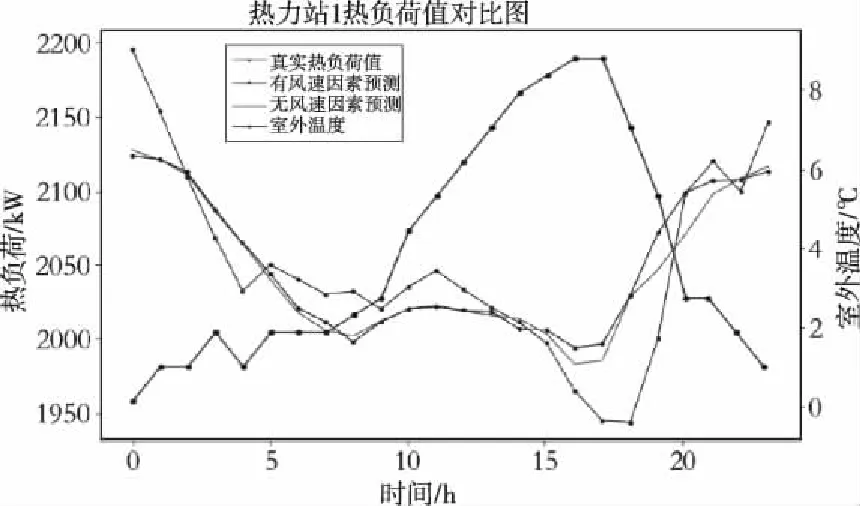
图10 热力站1有无风力热负荷值对比图

图11 热力站2有无风力因素相对误差对比图

图12 热力站2有无风力因素热负荷值对比图

根据实验数据结果如表2所示。不难发现，在加入风力因素之后，热力站1和热力站2的平均相对误差分别降低了0.03%和0.17%。通过验证未来24小时的热负荷值，可以看出来，热负荷和气温基本呈反比的关系，热负荷会随着气温的降低而升高，特别是16时之后的热负荷，尤其明显，因为在0时-10时的阶段，温度变化基本在零下1℃到零上2℃阶段变化，而11时-23时温差变化明显，因此热负荷值也会产生较为明显的变化，这也符合包头市温度变化趋势。因此，这项实验为热负荷预测的准确提供了理论依据，并且精度满足实验要求。将该模型与SVM的三种核函数进行预测对比。SVM是针对二分类问题提出的一种算法，使得超平面距离最近的样本点的距离最大，在处理类似区域供热系统的问题时，常用核函数来解决训练样本线性不可分的问题，典型核函数包括线性核函数、多项式核函数和径向基(Radial Basis Function，RBF)核函数，为了验证SVM的预测性能，以热力站1有风力因素数据为例，仿真过程采用与LSTM相同的环境条件和一致的输入数据，验证集同样为最后一天的24组数据，如表3为其各项指标对比。对三种方法求相对误差并可视化预测结果如图13和14所示。

表2 有无风力因素对比结果

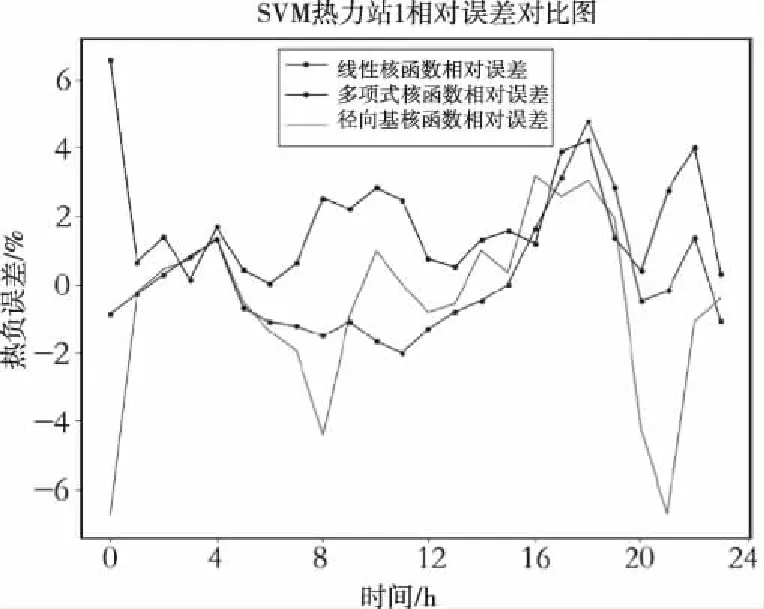
图13 SVM三种核函数预测相对误差

图14 SVM三种核函数预测结果

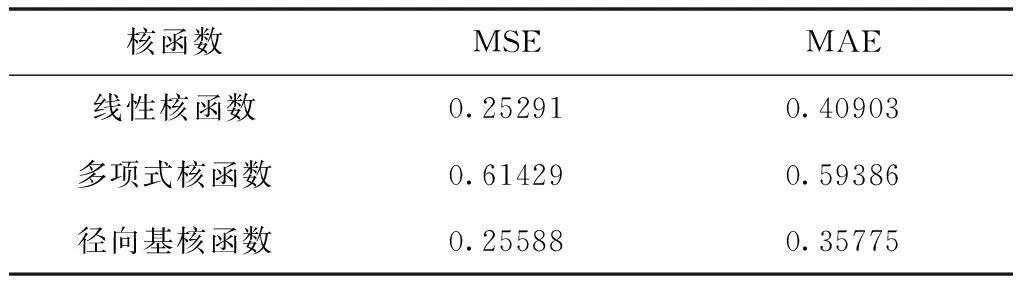
表3 SVM模型预测与指标对比

三种核函数的预测结果中，均方误差从大到小依次为，多项式>径向基>线性核函数，但是从其相对误差表现来看，表现最好的线性核函数最大相对误差为4.79%，平均相对误差为1.29%，相比于LSTM神经网络，最大相对误差高出了0.42%；径向基核函数最大相对误差(6.74%)比LSTM高出了2.37%，可见，对于时间序列的热负荷预测模型而言，长短期记忆神经网络更具有优势。

4 结束语

为了进一步提高热负荷预测精度，本文将深度学习框架LSTM神经网络模型作为热负荷的预测模型，算法研究表明：

1) LSTM模型可以更好的发掘历史数据之间的规律，模型中隐含层加入DropoutWrapper函数能有效防止过拟合，对模型的预测精度起到了促进作用。

2) 通过考虑风力因素对热负荷预测的影响，证明了其作为影响因素的重要性。

3) 采用大量真实历史数据进行对比实验，验证模型的有效性，同时与三种不同的核函数方法做对比分析，证明了所提方法的有效性。

综上，通过对热负荷的预测，得到未来时刻的热负荷值，这将为热量的优化控制研究奠定基础，有利于控制系统按照未来热负荷的变化情况去控制供水流量或者温度，对于按需供热和节能减排有重要意义。