基于移动边缘计算的区块链资源分配算法仿真

李 凡，王 超

(成都信息工程大学区块链产业学院，四川 成都 610225)

1 引言

移动边缘计算是现阶段能够实现资源计算、存储以及处理功能为一体的全新架构形式。该计算通常通过两种方式实现：一种是将需要处理的资源放置至基站或各种无线通信设施中，利用蜂窝移动通信或无线通信，实现就近处理数据服务；第二种是通过终端设备自身存在的数据处理能力，例如手机等设备，利用端到端等通信技术，完成本地数据处理。该计算方法能够有效降低服务响应时延，改善用户处理数据的难题，还能够缓解网络带宽以及电池容量压力等。

区块链技术最早是通过比特币形式展现到人们面前。该技术通过去中心化的管理结构，实现数据加密以及数据处理等问题。对于资源分配来说，通过移动边缘计算与区块链相结合的形式，能够全面、安全地实现资源的分配。有较多学者研究资源分配，例如翟玲等人研究云计算平台下电子信息资源均衡分配算法，唐伦等人，研究基于异步优势演员-评论家学习的服务功能链资源分配算法。以上几种算法在实际应用中仍然存在系统能耗过高的问题。

因此，本文研究一种新的基于移动边缘计算的区块链资源分配算法。通过构建基于区块链形式的资源管理结构，实现资源的去中心化管理，利用移动边缘计算，构建多用户异构蜂窝模型，并设计模型优化约束，采用蚁群算法获取资源分配最优解，实现最佳资源分配。

2 基于移动边缘计算的区块链资源分配

2.1 多用户异构蜂窝移动边缘计算模型

由于区块链中边缘网络资源自身存在计算资源不足以及电池容量不足难以进行高性能运算等问题，借助无线通信技术，将终端设备连接到移动边缘计算(MEC)服务器中，以此为基础，并结合上述去中心化管理后的资源，构建基于多用户异构蜂窝的移动边缘计算模型。

设计由一个以太坊主链和个以太坊侧链构成的多用户异构蜂窝网络。在以太坊主链的计算范围中，均匀存在个终端设备。设全部基站的集合为={，，…，}，以太坊主链由描述。终端设备的集合由={，…，}描述。将每个服务器分别放置在每个以太坊侧链中，使计算资源能够供应至终端设备。在每个设备中，存在一个具有延迟敏感性且计算较为密集的计算任务，设计算的任务的大小为，并设需要的计算资源为，并将某段时延内需实现的计算任务通过描述。

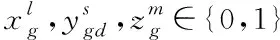
(1)

式(1)中，表示设备，设备与以太坊主链或以太坊侧链存在关联，同时，设备与基站互相通信时的传输速率与功率均会因带宽变化而变化，且当信道出现干扰时，也会对传输造成干扰。因此，为有效解决干扰，以太坊侧链复用以太坊主链的频谱资源，选取OFDMA实现设备与基站的通信。在此时，相同基站内的设备之间存在正交频谱，以太坊侧链与以太坊主链之间的频谱同样为正交。

若某一以太坊侧链的区域范围内不存在设备，则该设备的在以太坊主链上实现通信，两者的无线通信数据传输速率如式(2)所示

(2)

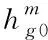
2.2 资源分配时延与能耗计算

可采用三种形式实现设备的计算任务：

1)通过本地计算资源对任务进行计算。

(3)

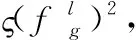
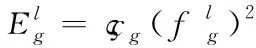
(4)

2)迁移至以太坊侧链上的服务器进行处理

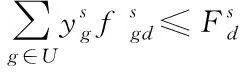
(5)

通过三部分实现设备将任务迁移到以太坊侧链中处理的延迟。首先是上行链路传输时间，其次是任务计算时间，最终为下行链路传输时间。由此可知，从设备中将任务转移至以太坊侧链进行计算的任务完成延迟可通过式(6)表示

(6)

与该公式相应的能耗如式(7)所示

(7)

式(8)中，以太坊侧链所采用的单位时钟能耗由描述。

3)迁移至以太坊上主链的服务器进行处理

该迁移过程与迁移至以太坊侧链过程较为类似。因此以，该过程的任务完成时延如式(8)所示

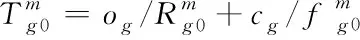
(8)

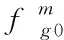
与该公式对应能耗可通过式(9)计算：

(9)

式(9)中，以太坊主链所采用的单位周期能耗由表示。

2.3 边缘计算能耗迁移与资源分配联合优化模型

考虑以太坊主链和以太坊侧链的计算资源约束、任务的时延约束，建立边缘计算能耗迁移与资源分配联合优化模型，如下所示：

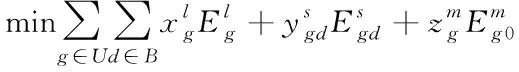
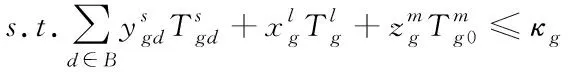
(10)

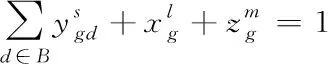
(11)

(12)

(13)

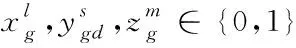
(14)

其中，表示计算资源总容量。式(10)表示任务的时延约束；式(11)、式(13)约束每个设备，使该设备仅能选取一种计算形式对任务进行计算，分别为本地计算、迁移到以太坊侧链或以太坊主链；式(12)是以太坊侧链或以太坊主链的计算资源约束，由于上述公式属于整数约束，因此对以上公式进行优化属于NP难问题，若想寻取该问题的最优解，需要将问题转化为蚁群算法学习模型，通过蚁群算法，对资源分配最优解进行寻取。

2.5 基于蚁群算法的模型求解

251 路径构建

依据蚁群算法的理论，选取蚂蚁“觅食”路径的形成与更新信息素的过程为该算法的主要步骤。其中，路径的形成通常是依据启发信息，寻取到蚂蚁由当前点移动到目的地的概率，之后挑选概率最高的点，将该点作为蚂蚁转移的下一目的地，以此为基础，确定蚂蚁逐步移动的路径，以确认蚂蚁整个移动的路径。

通过式(15)对蚂蚁移动概率进行计算

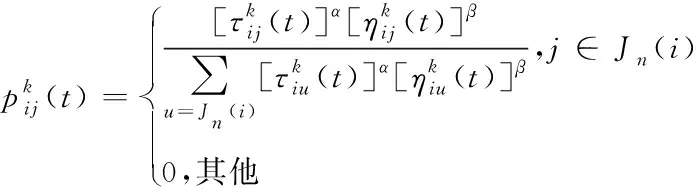
(15)

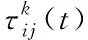
252 信息素更新

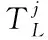
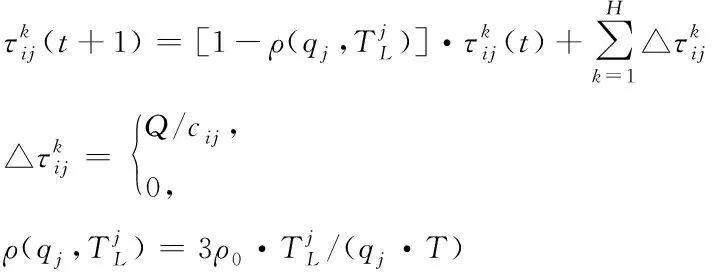
(16)

当全部路径信息素都实现更新时，引入下一轮蚂蚁，继续进行新一轮循环。式(16)中，表示路线，为需求点数量，的情况下表示蚂蚁经过，“0”情况下表示蚂蚁不经过，表示点到点的距离，。

253 蚁群算法求解基本流程

依据蚁群算法的基本理论，本文将资源分配求解过程分为四部分：第一部分为初始化，依据现实情况设定需要的参数；第二部分是确认蚂蚁群数目需求，将全部蚂蚁分组，并进行编号；第三部分为依据需求点数量，对蚂蚁进行随机分配，使蚂蚁的移动路径能够通过移动概率获知；第四部分是在全部蚂蚁都寻找到路径后，对最优目标值进行计算，计算结束后对路径中的信息素进行更新，更新完毕启动下一轮循环，当循环达到一定次数后，得到资源分配最优解。

1)对每条线路中的信息素(，=1，2，…，)，，，进行初始化。

2)对蚂蚁进行分组，全部蚂蚁分为组，在每组中存在只蚂蚁，向资源存放区域放置全部蚂蚁，即向位置派出资源分配小组。

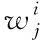
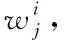
5)若步骤4)内的全部蚂蚁均返回至点，则执行步骤6)，若未返回，则执行步骤4)。

6)求解式(11)，获取现阶段最优解。

7)若现阶段所设循环次数大于迭代次数，则对每条路径中的信息素进行更新，并重新执行步骤2)，若未大于，则执行步骤8)。

8)依次对比循环中的目标函数值，获取全局最优解，实现区块链资源分配。

3 实验分析

通过Python对本文算法进行仿真，选取文献[6]云计算平台下电子信息资源均衡分配算法，文献[7]基于异步优势演员-评论家学习的服务功能链资源分配算法作为本文对比算法。

在单个移动终端的MEC服务器下，分析应用本文算法分配资源时，随着MEC服务器运行时间的增加，MEC服务器的电池能量与电池容量的消耗情况，分析结果如图1所示。

图1 应用本文算法后电池消耗情况

根据图1可知，随着运行时间的增长，电池容量始终消耗为40mJ，并未随着时间增长而产生波动，而MEC服务器运行时间处于0ms时，并未开始分配资源，因此电池能量消耗为0，当开始分配资源，电池能量的消耗由此上升，达到30mJ～40mJ之间，在之后的时间里，始终消耗电池能量均处于30mJ～40mJ之间，因此，应用本文算法，并未产生较大的电池消耗，能够以较为节约电池能量的形式实现资源的分配。

分析采用三种算法对资源进行分配时在不同设备数量下的资源分配能耗，分析结果如图2所示。

图2 不同算法分配下的能耗变化情况

根据图2可知，当设备数量逐渐上升，三种算法资源分配能耗也随之增加，其中，文献[7]算法的资源分配能耗在三种算法中保持最高，当设备数量达到150个时，能耗达到1600mJ以上，文献[6]算法的资源分配能耗相对低于文献[7]算法，但该算法的能耗会随着设备数量的增加大幅度上升，且该算法资源分配下的能耗要高于本文算法，本文算法未出现资源分配能耗大幅度上升现象，且最高能耗不超过400mJ，因此，应用本文算法对资源进行分配时，并不会对MEC服务器造成太大负担。

分析三种算法处于同一用户数量时，随着计算迭代次数的增加，不同算法地计算资源分配收敛状态，分析结果如图3所示。

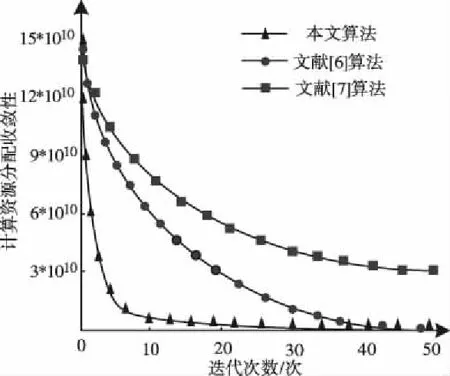
图3 三种算法的计算资源分配收敛性

根据图3可知，当计算迭代次数逐渐增加，三种算法逐渐进行收敛，其中文献[7]算法在迭代次数为50次时并未实现有效收敛，因此该算法的收敛性能最差，文献[6]算法虽然能够有效实现收敛，但本文算法的收敛情况依然高于该算法，本文算法在迭代次数为30次时，即能够完整实现资源分配收敛，因此，本文算法能够在有限迭代次数内实现收敛状态。

当用户数量分别处于50，100，150时，分析应用本文算法计算过程中，当移动边缘的最大发射功率逐渐增长时，资源分配速率的变化情况，分析结果如图4所示。

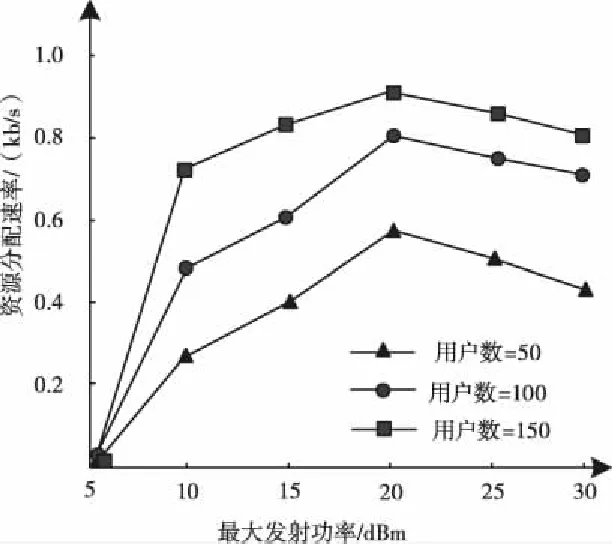
图4 不同用户数量下的资源分配速率

由图4可知，当用户数量增大，资源分配速率也随之增大，但当最大发射功率为20dBm之后，速率开始逐渐下降，因此在功率为20dBm时，资源分配速率也停止增加，同时，用户数为150名时，资源分配速率最高。

4 结论

本文研究基于移动边缘计算的区块链资源分配算法，通过构建区块链形式的数据管理结构，并结合移动边缘计算，构建多用户异构蜂窝移动边缘计算模型，设计资源分配优化约束，依据优化约束模型，采用蚁群算法获取全局最优解，实现资源分配。通过仿真形式验证算法性能，得出该算法收敛状态与系统能耗均要好于其它算法。未来可依据当前设计继续优化，实现海量数据资源的分配。