基于种群熵的变步长布谷鸟搜索算法
2022-10-25刘洪达李德全
刘洪达,李德全,王 栋
(1. 中国科学院长春光学精密机械与物理研究所,吉林 长春 130033; 2. 中国科学院大学,北京 100049)
1 引言
随着科学技术的发展,最优化问题成为了各个领域的重点研究对象。由于各行各业提出的最优化问题变得越来越抽象复杂,存在着非线性约束、计算量大等问题,经典的优化计算方法已经无法满足实际的需求。为获得复杂的优化问题合理有效的近似解,研究者们基于没有免费午餐(No Free Lunch,NFL)定理,针对不同的优化问题设计了大量的元启发式算法,例如模仿动物种群群集行为的粒子群优化算法(Particle Swarm Optimization,PSO)、模拟自然选择与生物进化过程的遗传算法(Genetic Algorithm,GA)、模仿蜜蜂行为的人工蜂群算法(Artificial Bee Colony Algorithm,ABC)等。在这些元启发式算法的基础上,诸多研究者对算法进行改进,提出了诸多改进策略,从而提高算法的效率。
许多优化算法由于其算法简单、易于实现等优点受人青睐,比如剑桥大学的Yang 和Deb于2009年提出的布谷鸟搜索算法(Cuckoo Search,CS)。这是一种通过模拟布谷鸟寻窝产卵的行为所设计的优化算法,基于莱维飞行机制进行寻优,能够有效解决最优化问题,并成功应用于图像处理、系统设计、医学应用、数据挖掘等各个领域的实际问题中,也可与其它算法相结合以提高混合算法的性能,如BP神经网络、PSO算法、极限学习机等。该算法简单、参数少,易于实现、全局搜索能力强,采用的随机搜索策略使得算法更为高效。此外CS算法的通用性强,可以与其它算法相结合。但是CS算法也和诸多元启发式算法一样,存在着后期的搜索效率低、寻优精度不高等缺点。
为了克服这些缺点,研究者们纷纷对CS算法进行改进:Rodrigues、冯登科等学者将二进制这一概念引入了CS算法中,获得了更优秀的全局搜索能力与鲁棒性,但仍存在一些收敛速度较差的问题;Ouaarab、王超等学者提出了一类离散CS算法,但是面对一些条件时提高效果并不明显;马英辉、Wang等学者将混沌理论引入到CS算法中,提高了寻优速度与精度,但是算法复杂度增大,影响了寻优时间。
针对CS算法存在的问题,本文通过种群熵对布谷鸟步长控制因子进行改进:将寻优搜索空间等分为多个子空间,计算种群熵以确定种群的分布特性,基于分布特性控制步长控制因子实时变化,从而提高了算法的寻优效率。此外,这项改进保持了CS算法的通用性,可配合其它改进策略来进一步提高算法的性能。
2 布谷鸟搜索算法
布谷鸟算法(Cuckoo Search,CS)通过模拟布谷鸟巢寄生繁殖的原理,利用莱维飞行机制(Levy Flight)来有效地求解最优化问题。
部分布谷鸟不会自己孵卵育雏,而是偷偷地在其它鸟类的巢穴中产卵,并移除相同数量的寄主卵,从而保持巢穴内的卵总数不变,最终由该寄主代为孵化育雏。若寄生卵被发现,此寄生卵将会被寄主移除,导致布谷鸟的寄生繁殖失败。
莱维飞行是一种混合了短距离与长距离的随机游走机制。其步长服从于重尾分布,随机游走过程中有相对较高的几率出现大的步长。而对于搜索算法而言,前期的大步长便于增强种群多样性,提高前期的全局搜索能力,易于搜索到全局最优值所在邻域;后期的小步长提高了局部搜索能力,缩小了搜索范围,从而获得全局最优解。
CS算法通过假设三个理想条件来模拟布谷鸟的巢寄生繁殖机制:
1)布谷鸟一次仅产一个蛋,并随机选择宿主巢穴来孵化自己的蛋;
2)在随机选择的一组巢穴中,孵化条件最好的巢穴将会被保留到下一代;
3)可寄生的宿主巢穴数量是固定的,一个宿主巢穴的主人能发现一个寄生鸟蛋的概率∈[0,1]。
在以上3个理想条件的基础上,基于莱维飞行机制的位置更新公式如下
+1=+(-)⊕′()
(1)
其中莱维飞行可以利用Mantegna方法进行模拟
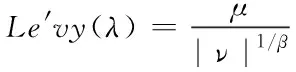
(2)
式(1)中,+1与为第+1代与第代的宿主巢穴位置,为当前最优解,为步长控制因子,⊕为点对点乘法,()为莱维飞行公式。
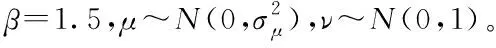
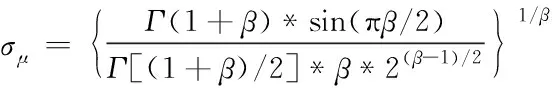
(3)
宿主鸟发现寄生鸟蛋的概率称为发现概率,在算法中常取=025。算法通过莱维飞行更新位置后,生成一个随机数∈[0,1],当>时,则对进行随机改变,采用偏好游走的方式生成等量的新解以替换旧解,象征着宿主发现并处理掉寄生鸟蛋的行为,使得布谷鸟随机选择一个新的巢穴进行寄生繁殖。偏好游走公式如式(4)所示
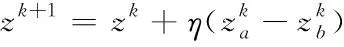
(4)
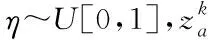
在处理实际的优化问题时,巢穴的位置代表待辨识变量的解值,巢穴的适应度代表待辨识变量取不同解的时候对应的目标函数值。算法的实现过程如下:
1) 参数初始化。设置最大迭代次数、种群规模、搜索空间维度、搜索上下界,生成鸟巢初始位置=(,,…,),并定义目标函数为(),=1,2,…,;
2) 计算每个巢穴的对应适应度,选出最优函数值作为当前最优适应度;
3) 基于莱维飞行机制,利用式(1)对巢穴的位置进行更新,获得一组新的巢穴位置并计算对应的适应度,此时式(1)中的步长控制因子=001。选择新巢穴的最优适应度与更新前的巢穴最优适应度进行对比,获得当前最优适应度与当前最优巢穴位置;
4) 随机产生一个随机数,令与进行比较。若大于则利用式(4)对巢穴位置进行随机更新,否则巢穴位置不发生变化;
5) 若达到最大迭代次数或满足指定搜索精度时,输出全局最优巢穴位置,即全局最优解,否则循环步骤2-4。
3 改进布谷鸟搜索算法
由式(2)与式(3)可知,Levy(λ)的值取决于正态分布随机数μ和v这导致莱维飞行搜索步长和方向都是高度随机变化的。对于步长控制因子而言,较大的控制因子可以增强全局搜索能力,但是局部搜索能力较差,容易造成搜索至在真值附近摆动;较小的控制因子会导致算法的效率低下,需要更多的迭代次数。为改善该问题,本文提出了PE-VSCS算法(Variable Step-size Cuckoo Search based on Population Entropy),将种群的分布熵引入到CS算法中,对步长控制因子进行改进。
熵为某一系统体系混乱程度的度量,种群熵为算法寻优过程中种群分布混乱程度的度量。假设布谷鸟种群总数为、搜索维度为,将寻优搜索空间分为个搜索子空间,每个子空间含有个体数为(=1,2,…,),则第维度(=1,2,…,)的分布熵为

(5)
式(5)为布谷鸟种群在寻优搜索空间中的分布熵的表达式。为使分布熵更能体现出寻优解的分布信息,一般搜索子空间取较大值。越大,则种群越分散,表明算法未收敛,需要较大的更新步长进行全局搜索;越小,则种群越集中,表明算法开始收敛,需要较小的更新步长进行局部搜索。
为满足上述关系,对改进步长控制因子进行构造,其表达式如下
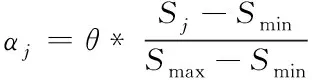
(6)
式中,为第维的步长控制因子,=0为分布熵理论最小值,=为分布熵的理论最大值,为调整参数。由于一般>,由式(5)可知,分布熵实际最小值为0,实际最大值为
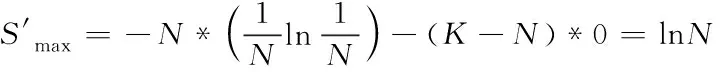
(7)
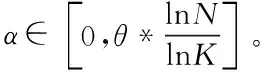
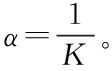
PE-VSCS算法的实现过程如下:
1) 参数初始化。设置最大迭代次数、种群规模、搜索空间维度、搜索上下界、搜索子空间数量,生成鸟巢初始位置=(,,…,),并定义目标函数为(),=1,2,…,;
2) 计算每个巢穴的对应适应度,选出最优函数值作为当前最优适应度;
3) 基于莱维飞行机制,利用式(1)对巢穴的位置进行更新,获得一组新的巢穴位置并计算对应的适应度,此时步长控制因子由式(6)决定。选择新巢穴的最优适应度与更新前的巢穴最优适应度进行对比,获得当前最优适应度与当前最优巢穴位置;
4) 随机产生一个随机数,令与进行比较。若大于则利用式(4)对巢穴位置进行随机更新,否则巢穴位置不发生变化;
5) 若达到最大迭代次数或满足指定搜索精度时,输出全局最优巢穴位置,即全局最优解,否则循环步骤2-4。
4 仿真研究
为验证PE-VSCS算法的寻优性能,本文选用了如表1所示的不同特点的测试函数。针对不同的测试函数,利用PE-VSCS算法与CS算法各进行50次仿真,并记录结果进行分析。其中()-()为多维函数,()-()为二维函数,()、()、()、()为多峰函数,其余为单峰函数。
记录每一次的仿真结果,将50次仿真结果中的最优值、最差值、平均值、标准差作为算法性能的评价指标。最优值代表了算法寻优可达到的精度上限,平均值代表了算法寻优的平均精度,标准差代表了算法的稳定性。
测试结果如表3至表10所示。图1至图8为PE-VSCS与CS算法的最优收敛曲线图,图1至图4所示曲线图的维度取值为10,图5至图8所示曲线图的维度取值为2。
4.1 测试函数

表1 测试函数
4.2 测试环境与算法参数
仿真环境操作系统为7,为5-6400 27,运行内存为8,编程环境为2014。
算法的最大迭代次数根据测试函数的搜索难度适当调整。其余的参数设置见表2。
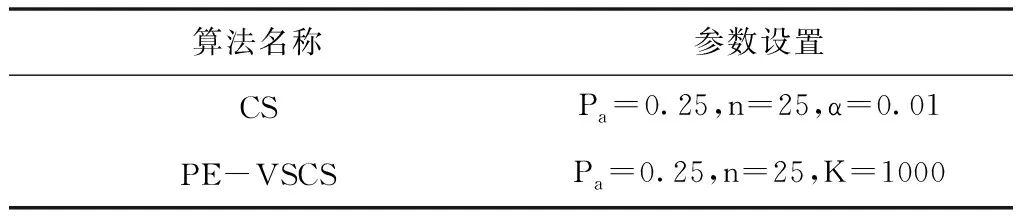
表2 算法参数设置
4.3 算法性能比较
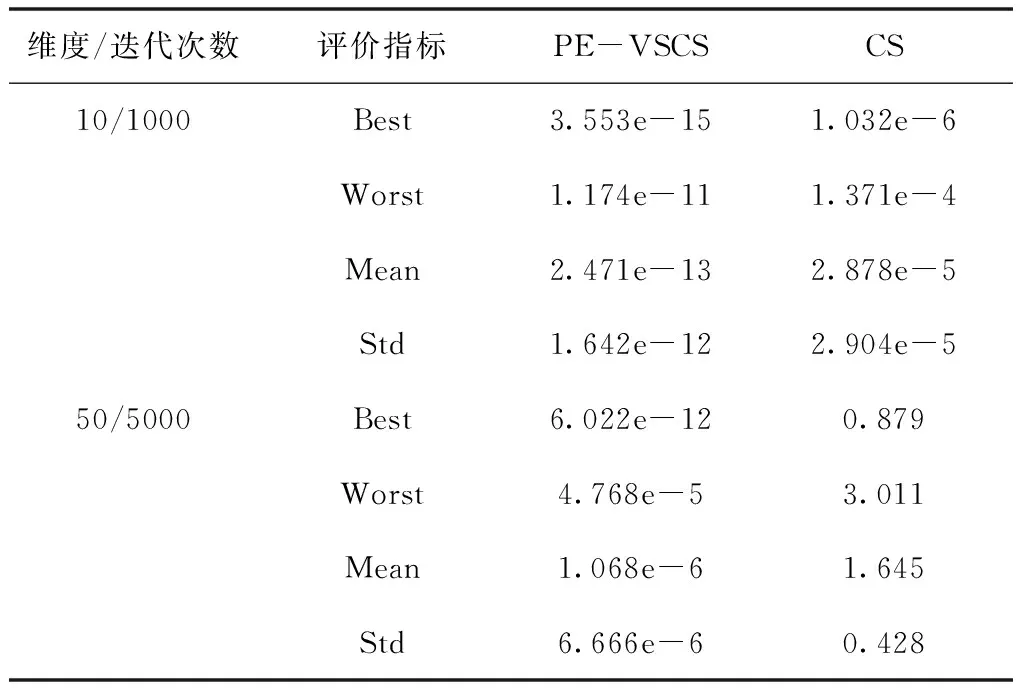
表3 Ackley函数f1(x)仿真结果
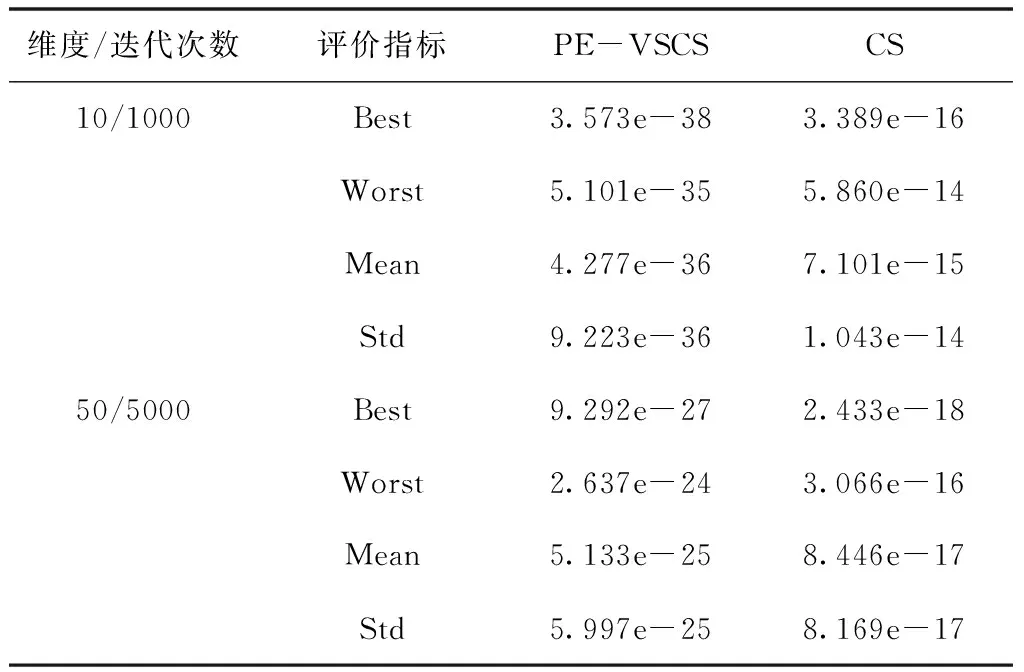
表4 Sphere函数f2(x)仿真结果
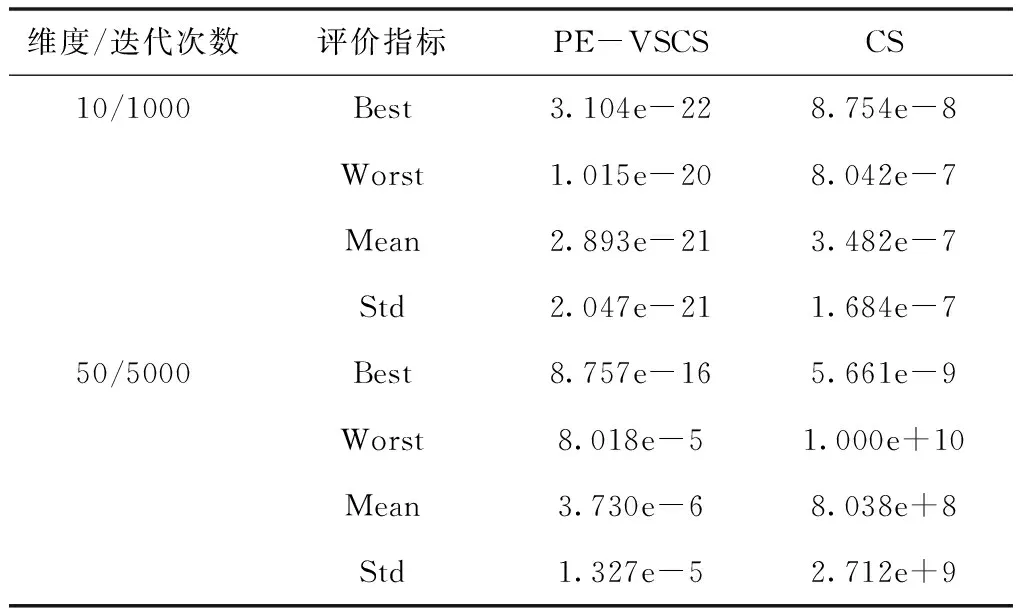
表5 Schwefel’s P2.22函数f3(x)仿真结果

表6 Sum Square函数f4(x)仿真结果
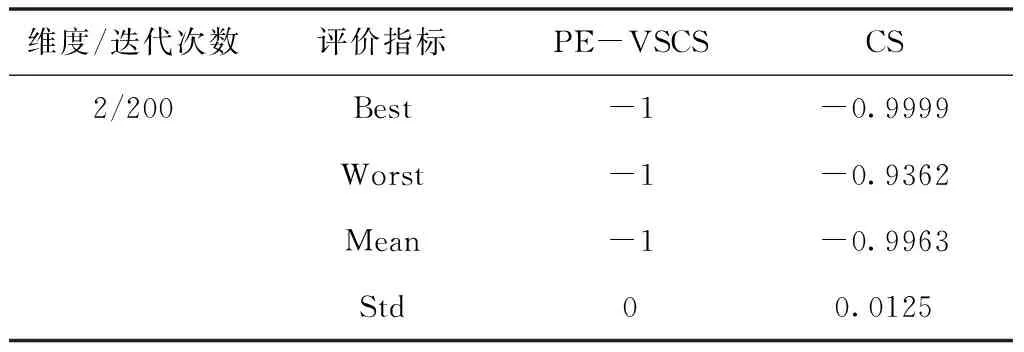
表7 Drop-Wave函数f5(x)仿真结果
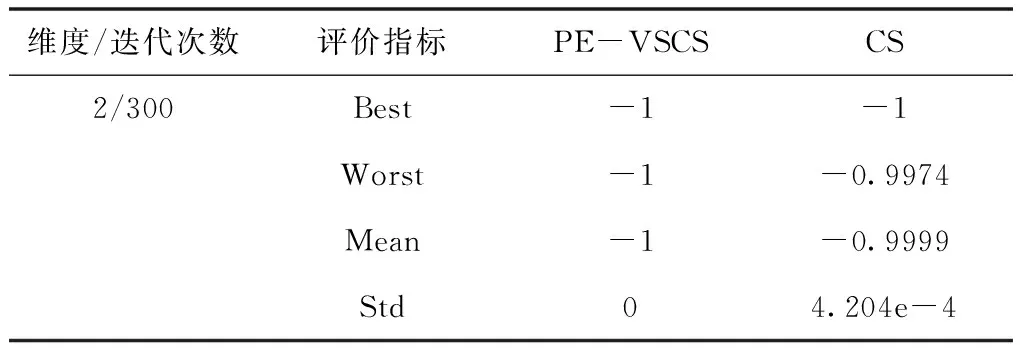
表8 Easom函数f6(x)仿真结果
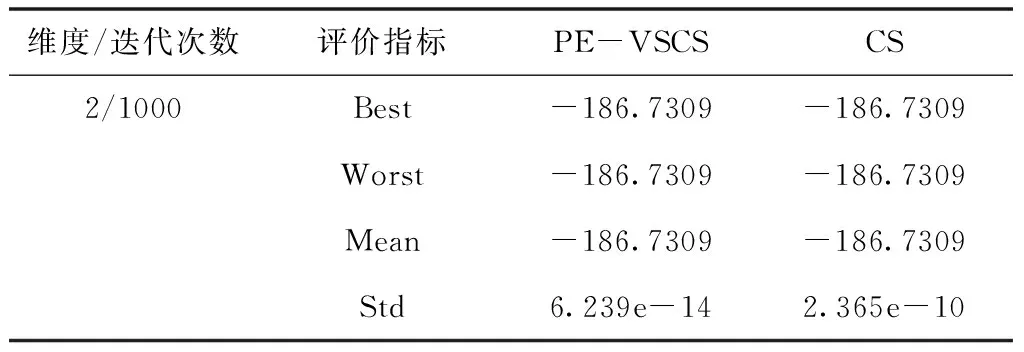
表9 Shubert函数f7(x)仿真结果
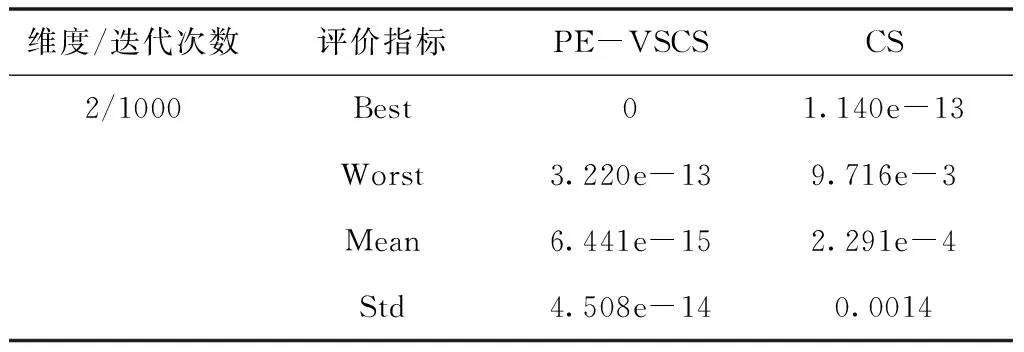
表10 Schaffer函数f8(x)仿真结果
由上述测试结果可以看出,与CS算法进行对比,PE-VSCS算法的性能大幅度提高。
面对低维度寻优问题时,PE-VSCS算法的收敛速度更快。从表7与表8可以看出,在面对一些较简单的测试函数时,PE-VSCS算法能在最大迭代次数较少的情况下,获得最优值并使得标准差为0,表明面对该类问题时,PE-VSCS算法能得到最优解且稳定性高。而CS算法在同样的最大迭代次数内,无法稳定寻出最优值甚至无法寻出最优值。从表9与表10可以看出,面对一些难度较高的测试函数时,PE-VSCS算法的四个评价指标的数量级均小于CS算法的评价指标数量级,表明PE-VSCS算法的稳定性与寻优精度优于CS算法。
面对多维问题时,PE-VSCS算法能达到一个很高的精度,优于CS算法。从表4与表6可以看出,PE-VSCS算法可以使得评价函数的数量级达到-30甚至-40,在一些实际问题中该数量级的误差可近似视为0。而CS算法所达到的数量级与PE-VSCS算法相比,数量级相差了10甚至20,表明了PE-VSCS算法的寻优精度要强于CS算法。
随着寻优维度的增加,PE-VSCS算法的寻优能力有所下降,如表3至表6所示,当寻优维度为50时,需要的迭代次数相比于10维度而言变大,且四个评价指标相比于低维度的寻优精度而言变差。但是与CS算法相比,仍有显著的提高,PE-VSCS算法与CS算法的四个指标相差至少5个数量级。
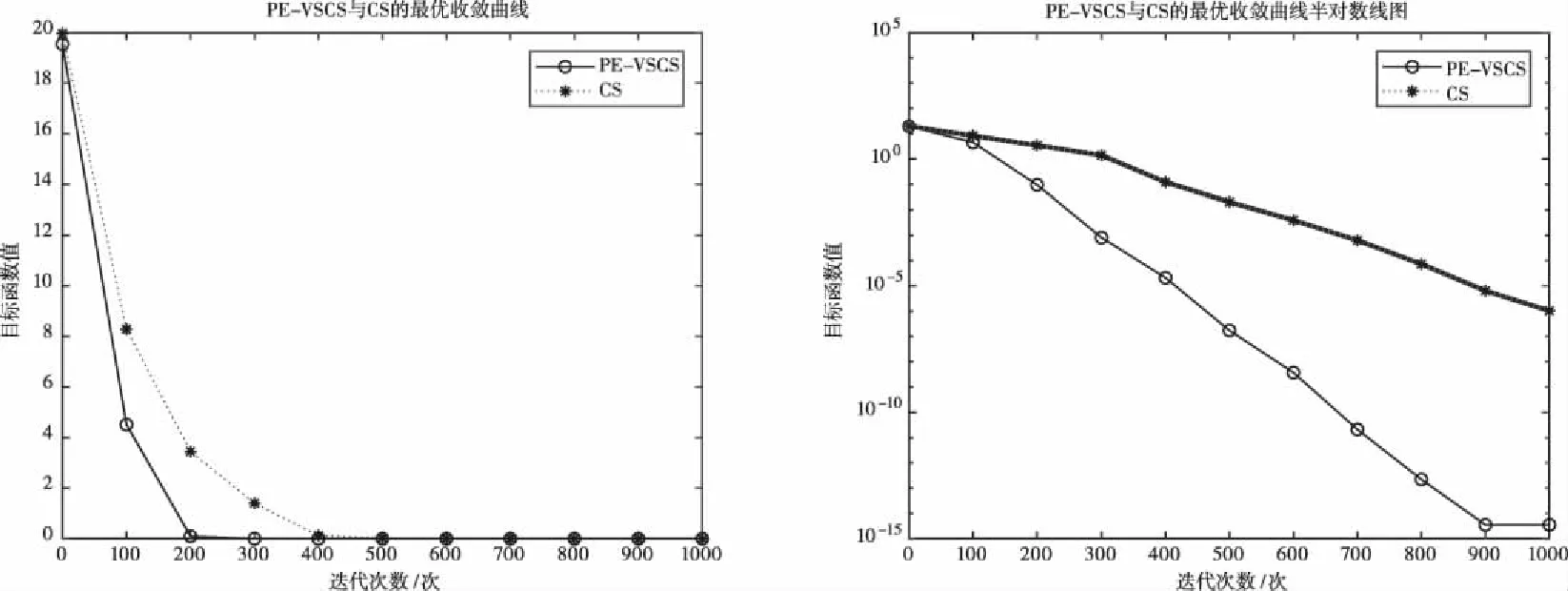
图1 基于f1(x)的PE-VSCS与CS算法的最优收敛曲线图

图2 基于f2(x)的PE-VSCS与CS算法的最优收敛曲线图
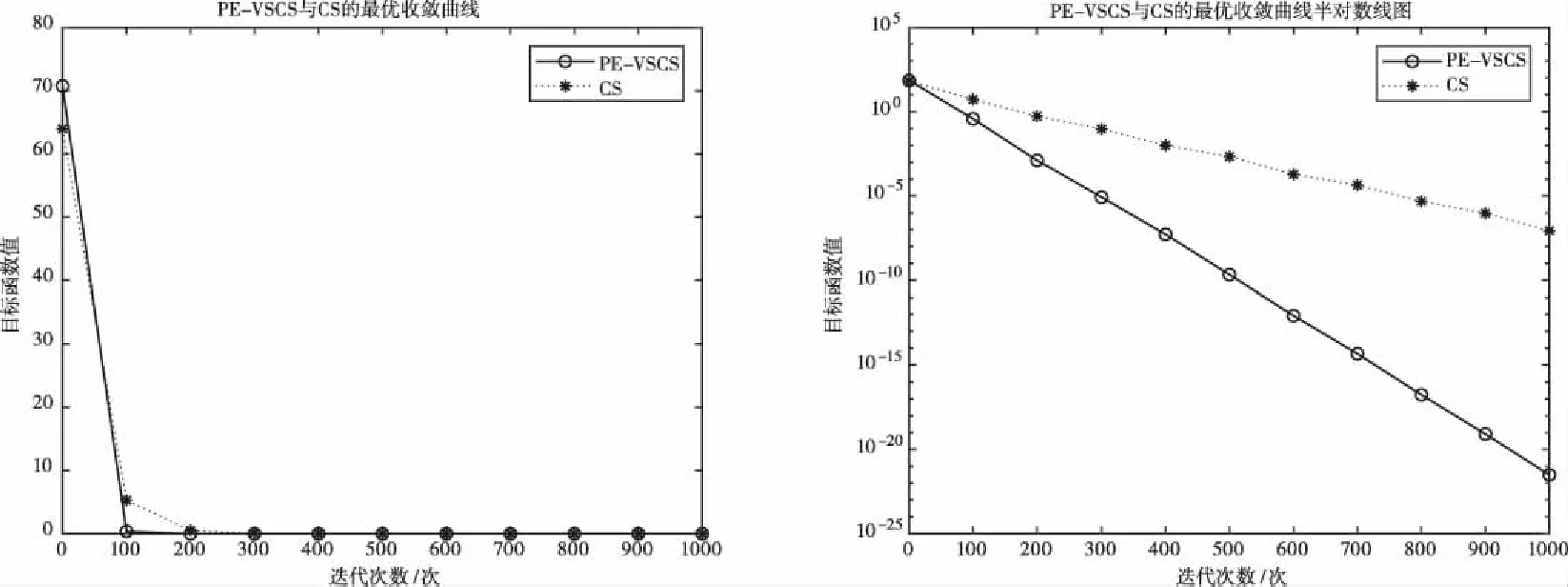
图3 基于f3(x)的PE-VSCS与CS算法的最优收敛曲线图
图4 基于f4(x)的PE-VSCS与CS算法的最优收敛曲线图
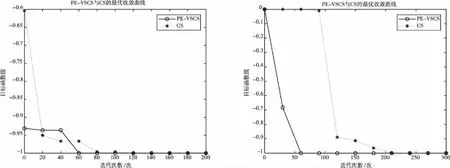
图5 基于f5(x)的PE-VSCS与CS算法的最优收敛曲线图 图6 基于f6(x)的PE-VSCS与CS算法的最优收敛曲线图
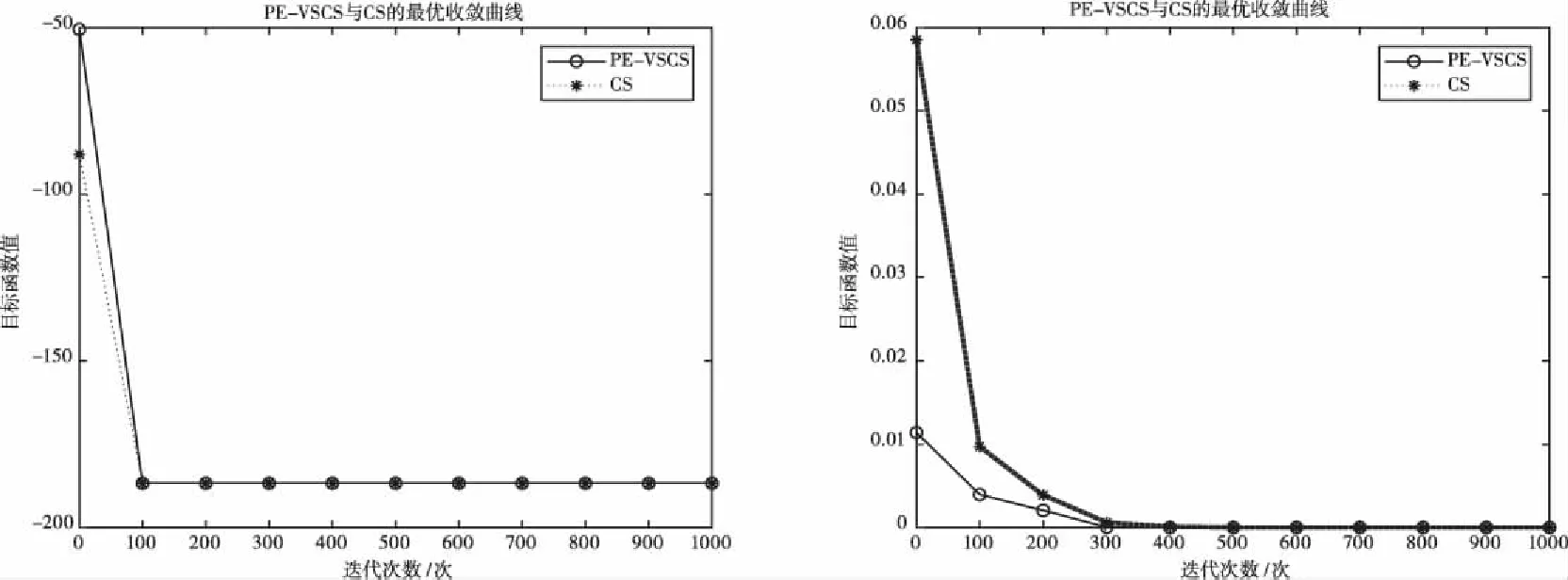
图7 基于f7(x)的PE-VSCS与CS算法的最优收敛曲线图 图8 基于f8(x)的PE-VSCS与CS算法的最优收敛曲线图
4.4 算法收敛曲线分析
图1至图4为10维度测试函数的收敛曲线与对应的半对数线图,图5至图8为二维度测试函数的收敛曲线图。
多峰函数f(x)、f(x)、f(x)、f(x)拥有多个局部极值点,可以测试算法跳出局部最优的能力。单峰函数f(x)、f(x)、f(x)、f(x)可以测试算法的收敛速度。由曲线图可以看出PE-VSCS算法的收敛速度要优于CS算法。由半对数线图可以看出PE-VSCS在指定最大迭代次数内,评价函数的量级要优于CS算法所能达到的量级。
综上所述,通过八个测试函数的收敛曲线图进行对比分析,无论是低维度寻优还是高维度寻优,无论是单峰函数还是多峰函数,PE-VSCS算法都具有优秀的寻优能力与收敛速度,证明了引入种群熵的步长控制因子的有效性
4.5 改进步长控制因子的分析
以Easom测试函数的测试结果的步长控制因子的变化为例,给出各维步长控制因子随迭代次数变化的曲线如图9所示。
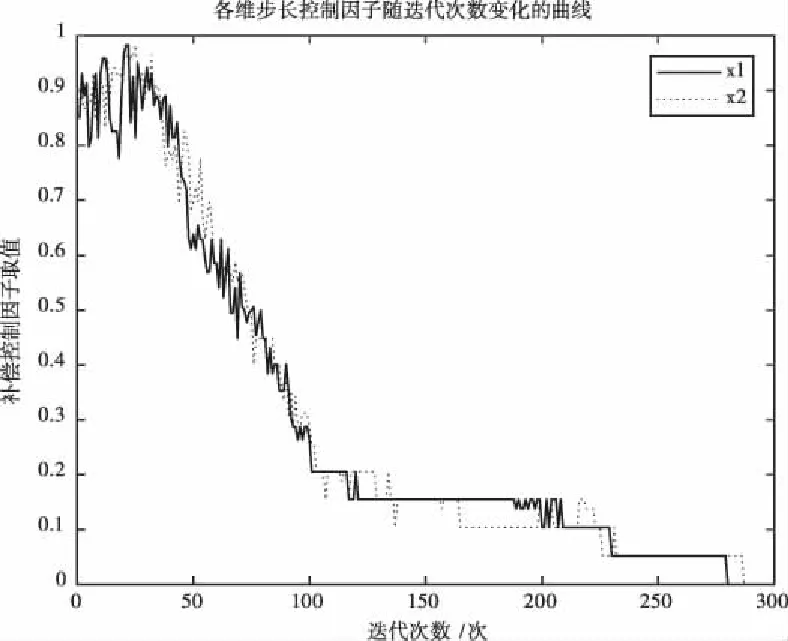
图9 各维步长控制因子随迭代次数变化的曲线
由图9可以看出,各维步长控制因子随种群熵不断变化,整体呈现下降趋势。在迭代初期时,步长控制因子取较大值以提高前期的全局搜索能力;迭代后期时,步长控制因子处于一个较小值,提高了局部搜索能力。在迭代过程中,步长控制因子会偶尔出现变大的情况,以对应由于随机更新导致的种群分散情况。算法随迭代次数的增加逐渐由全局搜索转为局部搜索。
5 总结
熵可以度量某一系统体系混乱程度,CS算法寻优模拟了布谷鸟种群从众多分散的巢穴中寻找出最优巢穴进行寄生繁殖的过程,种群从发散最终收敛于某一点,种群熵也随之变化从大变小。种群熵的变化代表了种群在寻优过程中的变化。本文通过将种群熵引入到莱维飞行机制中,构建了新的步长控制因子。通过8个测试函数的性能测试,可以表明PE-VSCS 算法的寻优能力、求解精度、收敛速度等方面相比于CS算法均有提高。仿真结果表明,无论是单峰函数还是多峰函数,无论是低维函数还是多维函数,PE-VSCS算法的寻优性能均超过CS算法,证明了基于种群熵的改进步长控制因子是有效的。且这项改进保持了CS算法的通用性,可配合其它改进策略来进一步提高算法的性能。本课题组将在后续工作中开展相关工作。
