奇数多涡卷混沌系统族及其FPGA实现

赵 耿，刘阿龙，马英杰

(1. 西安电子科技大学通信工程学院，陕西西安710071； 2. 北京电子科技学院电子与通信工程系，北京100070)

1 引言

随着时代更替和科学技术的不断发展，人们对信息传输的安全性提出了更高的要求，因此值得深入研究性能更加良好的调制信号来保障通信的安全。19世纪，混沌作为一门新兴学科登上了历史舞台，因为混沌信号具有非周期、类白噪声、相关性好、无法预测等很多优良特性，所以混沌信号源的构建已成为保密通信领域研究的热点。20世纪以来非线性动力学发展迅猛，这为混沌信号的构造提供了强有力的理论支撑，其中多涡卷混沌系统具有结构简单、动力学行为复杂、对初值敏感的特点，被广泛用于各种各样的通信系统中，目的是增强通信链路的抗干扰性和抗截获性。

近年来，Z. Tan、彭智俊、J. Liang、Y. Gao等学者们虽然提出了利用脉冲控制技术、正弦函数、对数函数、指数函数等非线性函数产生多涡卷混沌信号，但诸如此类方法具有局限性。本文在蔡氏电路和现有单涡卷、双涡卷混沌系统的研究基础上，引入组合符号函数，构建了一个能产生无穷奇数个涡卷的混沌系统。针对该模型，从动力学角度定性定量进行了分析，并且利用MATLAB仿真得到了李雅普诺夫指数谱、吸引子相图。在实际工程应用中，H. Liu、H. A. Jasim等人利用模拟电路实现了涡卷吸引子，但随着DSP、FPGA等大规模数字器件的盛行，利用数字信号处理的办法更加适用于保密通信领域。结合混沌的基本特征，本文利用FPGA开发平台进行了硬件实现。由于FPGA是高精度的数字信号处理器件，本文首先通过对提出的连续混沌模型进行离散化，然后使用Verilog HDL语言在赛灵思公司发布的集成设计环境Vivado 2018.3版本中以自底向上的数字化模式进行设计，其中关键模块可分为：浮点数运算模块、数值迭代模块、同步控制模块、浮点数转定点数模块等。根据工程的实际需要，最后结合示波器给出了基于ZYNQ7000开发平台的三维3涡卷、5涡卷、7涡卷混沌系统吸引子的硬件实验结果。理论仿真和硬件实验结果均表明：提出的奇数多涡卷混沌系统族稳定存在，并且涡卷数目可控。

2 可控奇数多涡卷混沌系统族

2.1 系统模型

本文在蔡氏电路和现有多涡卷混沌系统的研究之上，引入组合符号函数，构建了一个能产生无穷奇数个涡卷的混沌系统，其数学模型为

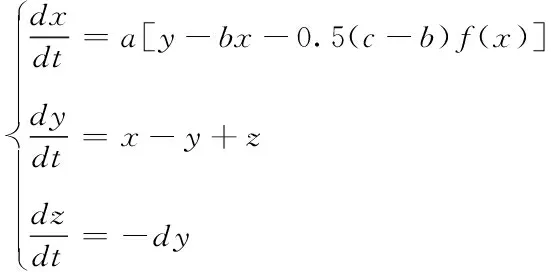
(1)

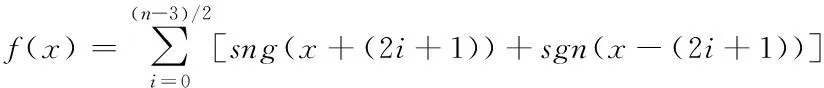
=3,5,7…

(2)

其中，、、为状态变量；、、、为实数参数；()为参变控制函数。将组合符号函数引入到多涡卷混沌系统，通过控制数学模型中维度的参变控制函数，可以产生一种新型无限延长的奇数(3、5、7……)多涡卷混沌信号源。与传统的单涡卷、双涡卷系统相比较，该系统具有更为丰富的吸引子相空间和更复杂的动力学行为。本文利用数字系统构建实现了三维3涡卷、5涡卷、7涡卷混沌系统，在实际的工程应用中更适合应用于保密通信。

2.2 复杂动力学特性分析及其数值仿真

本节将对2.1节提出的多涡卷混沌系统进行动力学分析和MATLAB的数值仿真。

对2.1节中系统模型，取a=9，b=2/7，c=-2/7，d=15；求解其平衡点得到

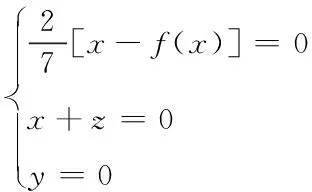
(3)

观察(3)式容易得到系统的平衡点为(，0，-)，其中为=()的根。根据平衡点的性质，为了使系统得到多涡卷吸引子，只需要增加系统的平衡点即可，即如果=()有多个实数根，方程组便有多个解，系统就能产生多涡卷的吸引子。令等于7，采用数形结合方法，便可以得到系统平衡点分布图，如图1所示。可以清楚的看到在每一个(2-1，2+1)区间内，()是连续函数，并且系统存在1个稳定平衡点，7个小的区间使系统具有7个平衡点；此外从图中看出还有6个第一类间断点，根据傅里叶级数敛散定理可知，()傅里叶级数收敛，并且当是()的连续点时，级数收敛于()；当是()的间断点时，级数收敛于(-0)+(+0)2。所以根据吸引子的特征，在每一个连续区间内系统能产生一个涡卷，而在每个间断点处系统都有一个同宿解，同宿轨将各个区间的涡卷连接起来，从而使系统形成7涡卷吸引子。根据上述分析可以得到，涡卷区域对应着系统的稳定平衡点，键波区域对应着系统的不稳定平衡点，所以，当一旦取定某一个大于等于3的奇数时，系统便能产生涡卷混沌吸引子。

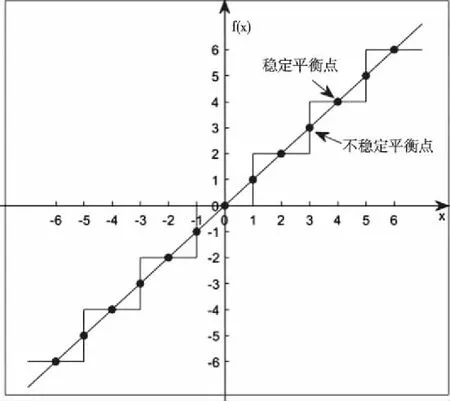
图1 系统平衡点分布图

取的值分别为3、5、7，则其分别对应3涡卷、5涡卷、7涡卷混沌系统，使用MATLAB仿真得到三个系统的李雅普诺夫指数谱均相同，如图2所示。其中X维度为LE1=0.166955，Y维度为LE2=0.166982，Z维度为LE3=-3.905366，李雅普诺夫维数为：LD=2.0854。根据混沌吸引子的特征，李雅普诺夫指数的计算均正确，并且无论n取任何一个奇数，总是能得到相同的李雅普诺夫指数谱，由此说明吸引子的性态不会随着涡卷数目的增加而改变，证明系统的稳定性良好。

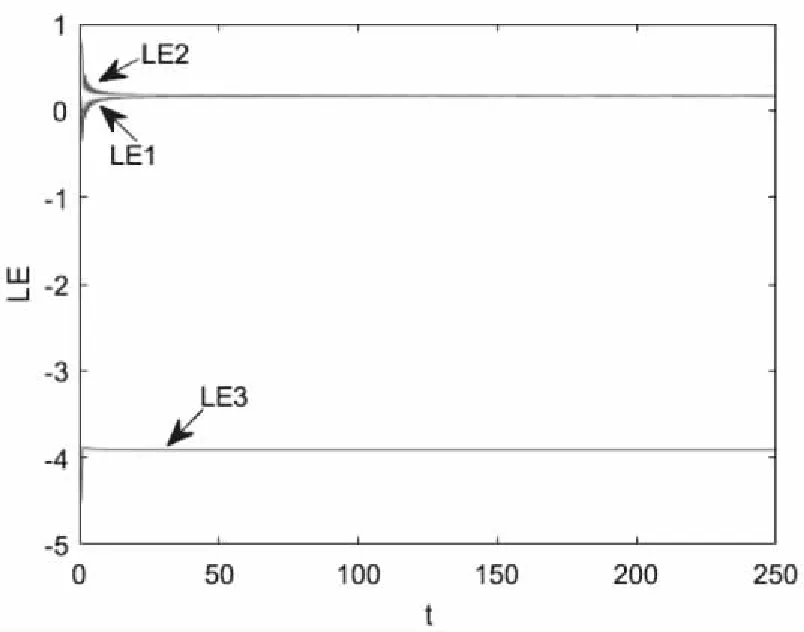
图2 3、5、7涡卷系统李雅普诺夫指数谱

3 基于FPGA的多涡卷混沌系统实现

3.1 系统整体架构

本系统使用Xilinx公司的ZYNQ7000开发平台，利用Verilog HDL语言在集成开发工具Vivado中进行自底向上的模块化数字设计模式，并使用Vivado内嵌的仿真器进行仿真验证。控制芯片选取XC7Z020-2CLG400I，DA模块选取AD9767 的双通道14位数模转换(DAC)板卡，示波器选取TDS3000B系列数字式荧光示波器。

系统整体构建方案如图3所示，具体可分为：三维方程设定模块控制涡卷的个数；浮点数运算模块实现数据的底层运算；数值迭代模块实现三维数据序列的迭代；同步控制模块实现数据的精准同步；浮点数转定点数模块实现数据的转换；两路数模转换模块将数字信号转换为模拟信号用于在示波器观察多涡卷的吸引子相图。

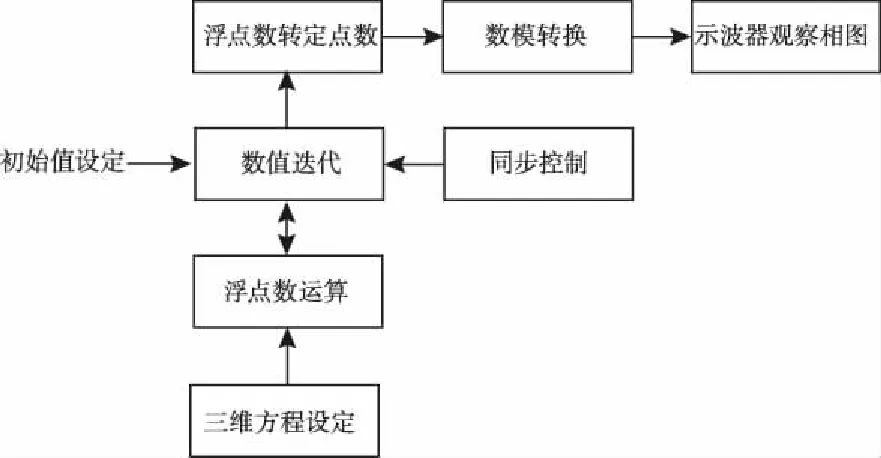
图3 系统整体架构

3.2 系统模型的离散化

本文所述的系统模型为三维连续型，由于FPGA通常用来处理离散数字信号，所以首先对该连续模型进行离散化。常见的离散化处理算法有简单Euler算法、改进的Euler算法和Runge-Kutta算法。简单Euler算法易于FPGA实现，占用的器件逻辑资源相对较少，但精度不算很高；而改进的Euler算法和Runge-Kutta算法虽然精度高，但同时实现难度较大，占用器件资源也多。本文考虑到工程实现的实际情况，下面采用简单Euler算法进行离散化处理。

简单Euler算法实际上是根据导数定义来实现的，导数的定义为

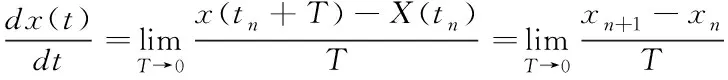
(4)

当的值趋于0或无穷小时，(4)式可表示为

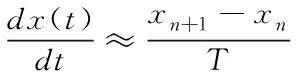
(5)

进而得到

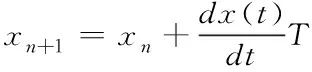
(6)

基于工程研究，本文选取步进因子=0005，将(6)式代入11节系统数学模型中，取()中分别为3、5、7得到多涡卷混沌系统迭代方程：(7)式为3涡卷混沌系统，(8)式为5涡卷混沌系统、(9)式为7涡卷混沌系统：

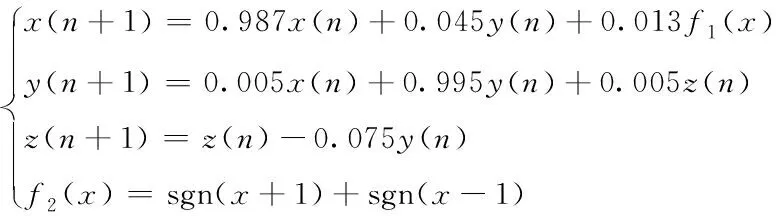
(7)

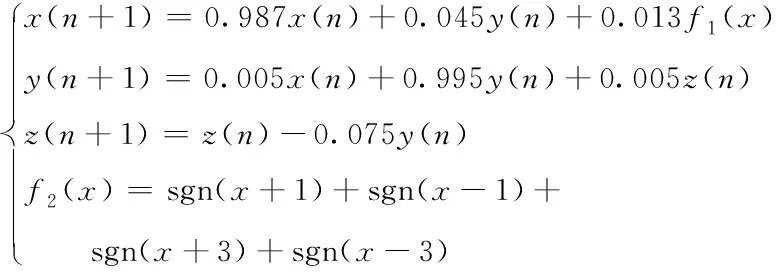
(8)

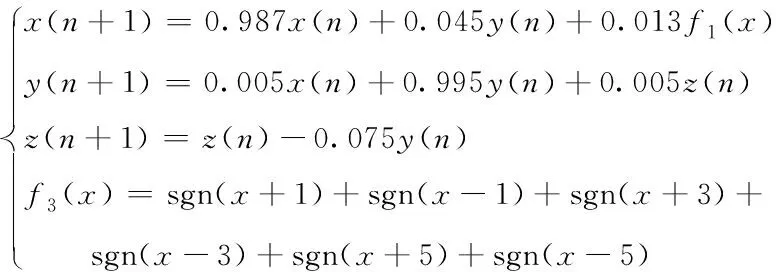
(9)

观察(7)式、(8)式、(9)式可知，()控制系统奇数涡卷的个数，因此只需要改变维度中符号函数的设定就可以选取对应的多涡卷混沌系统。MATLAB仿真得到离散化后的3涡卷、5涡卷、7涡卷混沌系统的吸引子空间结构如图4、图5、图6所示。

图4 3涡卷相空间结构

图5 5涡卷相空间结构

图6 7涡卷相空间结构

3.3 系统关键模块设计

3.3.1 浮点数运算模块

浮点数比定点数的表示范围宽，精度高，更适合用来进行工程计算。本文选用32位单精度浮点数，观察系统方程，浮点数运算包括加法、减法和乘法运算。根据IEEE 754标准，把32位二进制数据表示为1位符号位，8位阶码和23位尾数部分。

浮点数加法、减法模块设计方法如下：

浮点数减法可以理解为将做减法运算的数据对其符号位取反之后的加法，所以单独设定一个符号变换模块即可。加法运算步骤为：

1) 对阶：小阶向大阶对齐，目的是使操作数的小数点位置对齐；

2) 尾数运算：将对阶后的两个尾数按照定点的加减法运算规则计算；

3) 规格化：增加有效数字的位数，提高运算精度；

4) 舍入：考虑尾数右移时丢失的数值位；

5) 溢出判断：判断计算结果是否存在溢出。

浮点数乘法运算步骤为：

1) 符号位处理：符号位的判断运算单独处理；

2) 移位操作：操作数的小数点左移1位，阶码加1；

3) 尾数运算：尾数操作单独进行，按照定点的加减法运算规则计算；

4) 调整结果：按照浮点数的格式调整运算结果；

5) 规格化：获取尾数前半部分，判断是否四舍五入。

3.3.2 数值迭代模块

系统数值迭代顶层模块为scroll模块，其中例化了三维方程scroll＿x，scroll＿y和scroll＿z三个子模块，每个例化模块分别设定初始值x(0)=0.02，y(0)=0.01，z(0)=0.03，使用Vivado内嵌仿真器得到3涡卷、5涡卷、7涡卷部分数据迭代仿真波形如图7、图8、图9所示。

图7 3涡卷数值迭代

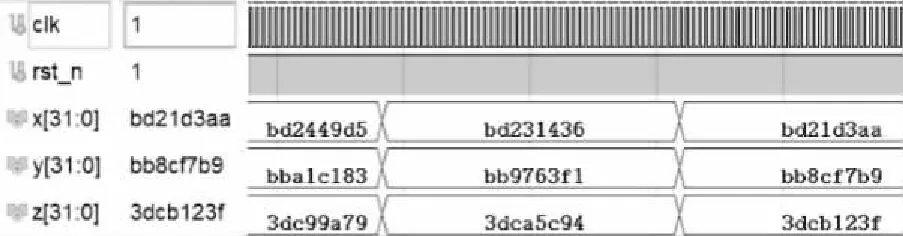
图8 5涡卷数值迭代

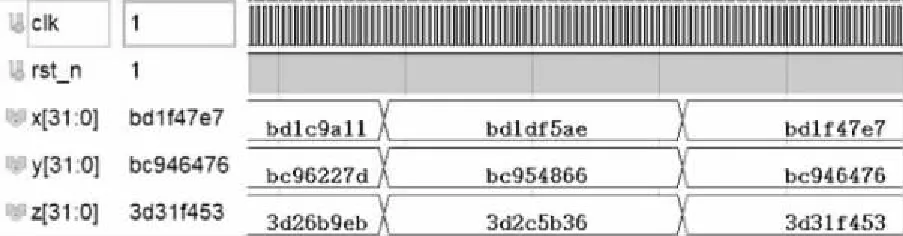
图9 7涡卷数值迭代

3.3.3 同步控制模块

数字电路因为路径的不同，一般存在各种各样的延时，这可能导致数据的丢失、乱码等现象，故为了保证不同路径数据同时到达输出端口，需要对各路径采取同步措施，仿真波形如图10所示，可以看出不同时钟下的3路数据经过同步处理之后都在同一时钟控制下输出，达到了同步的效果。

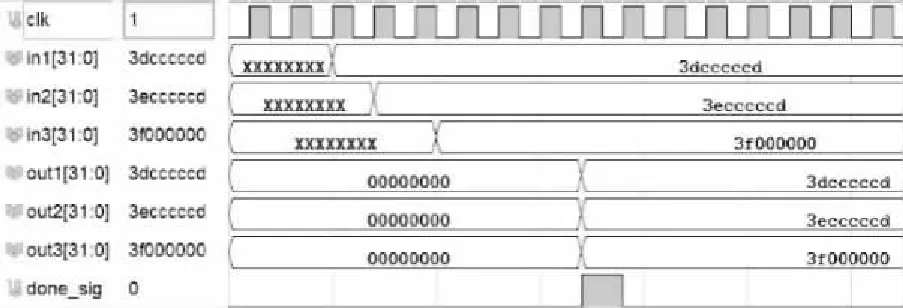
图10 同步控制波形图

3.3.4 浮点数转定点数模块

DA模块转换芯片的数据格式为14位双通道，为了匹配其输入格式，本系统将32位单精度浮点数转换为14位定点数，仿真波形如图11、图12、图13所示(截取部分数据)。DA模块将输入的数字混沌序列模拟输出到示波器，便于观察相图。

图11 3涡卷定点数

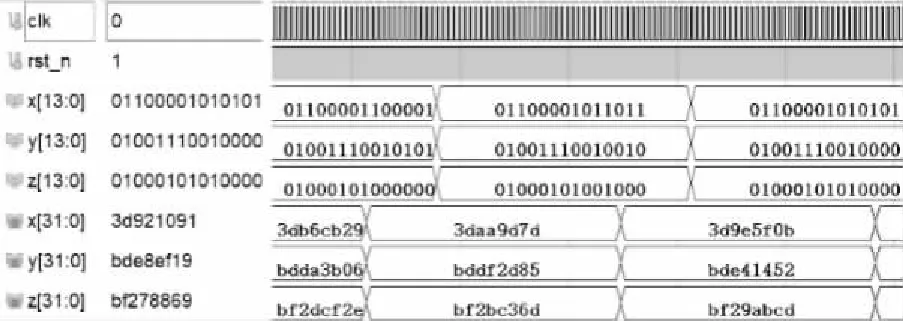
图12 5涡卷定点数

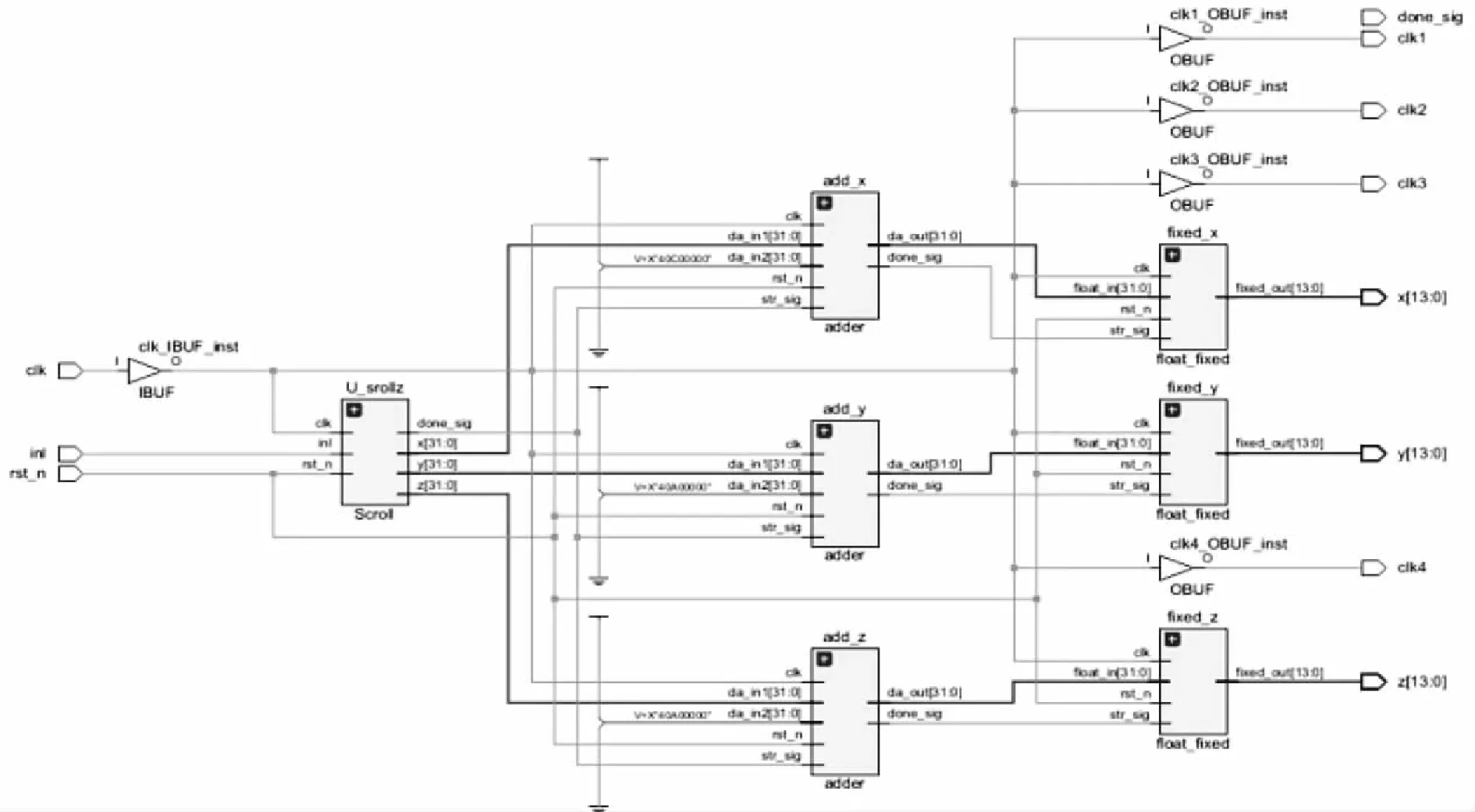
图14 5涡卷RTL视图

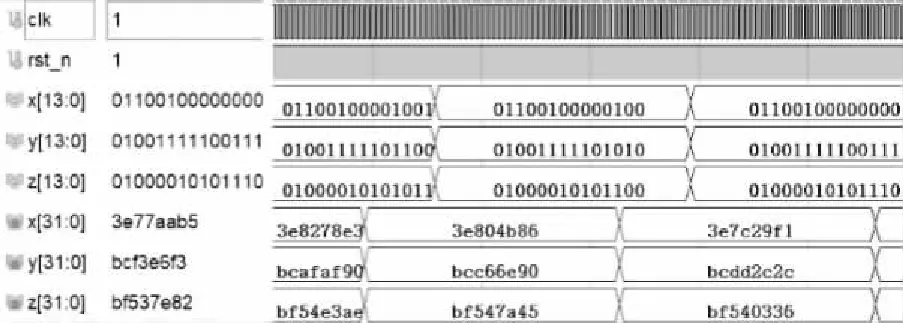
图13 7涡卷定点数

3.3.5 综合优化

以提高设计速度为目的，经过不断对代码优化，编写时序文件，使用集成环境Vivado对本工程编译综合，布局布线后导出了其硬件资源占用表，如表1所示，可以看出占用系统资源完全在可以容纳的范围之内。同时得到RTL视图，由于本系统任何涡卷的RTL视图模式都一样，选取5涡卷混沌系统为例，如图14所示。

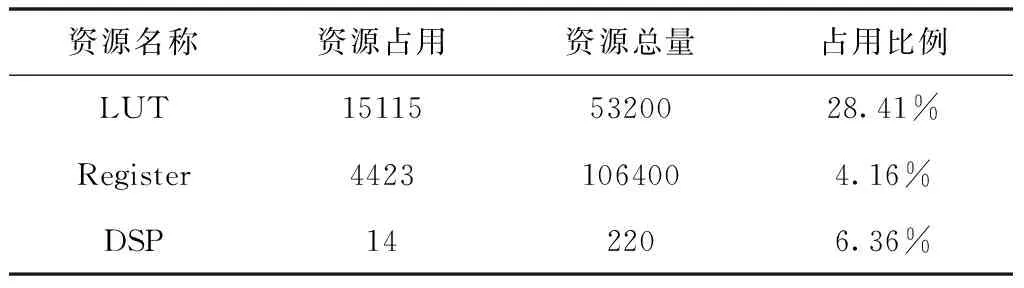
表1 系统资源占用表

3.4 系统板级验证实现

经过DA转换模块后，只能输出两路序列信号。因系统产生的是三维序列，所以调整顶层模块每次只输出二维x-y序列，x-z序列和y-z序列。最后调节示波器电压范围，成功得到了3涡卷、5涡卷、7涡卷的x-y相图、x-z相图、y-z相图。如图15、图16、图17、图18、图19、图20、图21、图22、图23所示。

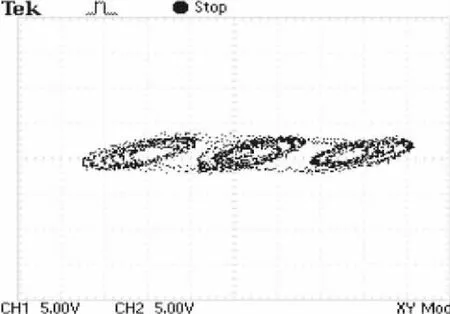
图15 3涡卷x-y相图

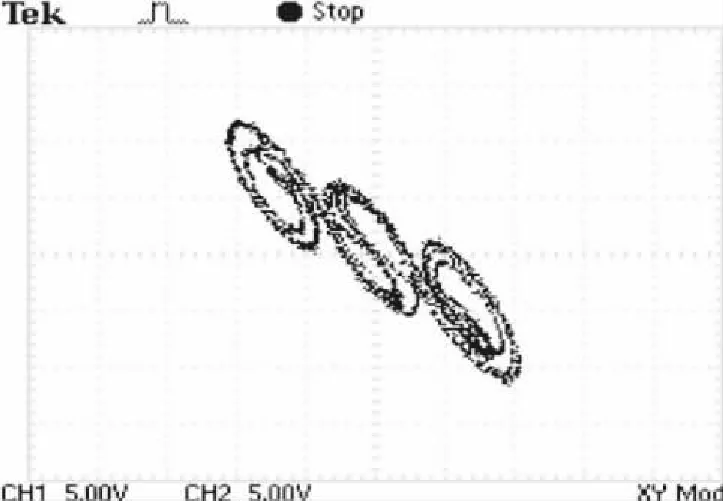
图16 3涡卷x-z相图

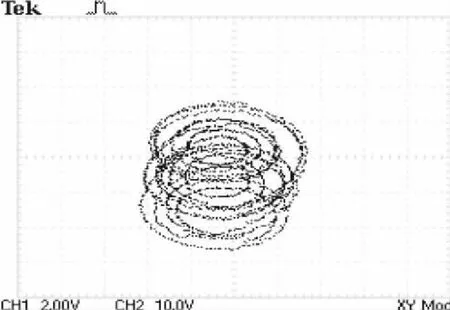
图17 3涡卷y-z相图

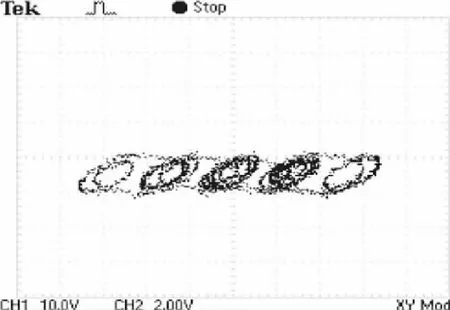
图18 5涡卷x-y相图

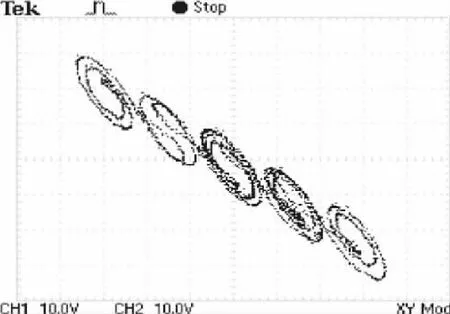
图19 5涡卷x-z相图

图20 5涡卷y-z相图

图21 7涡卷x-y相图

图22 7涡卷x-z相图

图23 7涡卷y-z相图

4 结束语

目前，信息泄露和截获事件普遍存在，尤其是军用保密通信领域，这极可能严重影响到国家的安全。传统单涡卷、多涡卷混沌系统性态简单，易于被破译和截获。针对此问题提出了一种基于符号函数的无限延长的奇数多涡卷混沌系统族。其主要优点为：1)不同于简单的单涡卷和双涡卷混沌系统，其可以根据实际场景的需求选择合适的涡卷个数；2)多涡卷的空间性态不可预测，大大增强了系统的安全性。

本文采用理论仿真和硬件实现的方法进行研究，首先使用MATLAB从理论仿真入手，通过对其动力学特性进性分析得到，其具有复杂的非线性动力学特定和丰富的相空间结构，完全相同的李雅普诺夫指数谱保障了系统结构稳定。然后为了进一步使该系统能在工程上得到实际应用，结合现代高精度数字信号处理器件FPGA对其进行了硬件实现。使用Verilog HDL语言，以自底向上的数字化模式进行RTL设计，以仿真作为辅助，在ZYNQ7000平台成功实现了3涡卷、5涡卷、7涡卷混沌系统，利用示波器得到了其吸引子相图。结合硬件实验结果看出本文仍存在一些值得改进的地方：1) 因为数字实现是离散的点数，所以硬件实验结果较仿真结果相似度没有达到100%，在以后的工作中可以选取精度更高的数字化离散方法，更好的逼近系统的混沌特性；2)从时序约束，资源利用率方向进一步优化RTL代码，提高运算速率；3)基于工程实际，按照此方法继续实现更多涡卷混沌系统，如9涡卷、11涡卷、13涡卷等等。