基于后向和多前车效应的跟驰建模及仿真

钱光宏，张立东，王小雷，宋晓帆

(山东交通学院交通与物流工程学院，山东济南 250357)

1 引言

交通出行与人类日常生活息息相关，数千年来，出行方式的演变见证了人类社会的发展历程。当前，随着汽车保有量的逐年攀升，交通拥堵已成为摆在各大城市面前亟需解决的问题。交通堵塞已严重影响了人们的日常出行、制约了社会经济的发展，由此引发的交通事故问题更是屡见不鲜。交通拥堵的成因机理在于交通供给与需求之间的不匹配，从而导致整个交通系统失稳，因此，解决交通堵塞就转变为如何提高整个交通流系统的稳定性。为了更好地描述交通流的运行特征及其拥堵成因，众多学者寄希望于通过数学的方法来解释复杂的交通现象，经过长达数十年的研究、改进和扩展，形成了各种各样的微观交通流模型。

Gipps提出了一种较为实用的安全距离模型，模型中认为车辆的运行速度由理想速度、道路状况所允许的最大加速度和安全车距这三者共同决定，虽然可以最大限度的保证安全，但其模拟的交通量与实际不符，不能反应真实的交通状况；Bando等人利用车间距优化速度函数对车辆跟驰行为进行了重新研究，建立了最优速度(Optimal Velocity，OV)模型，该模型形式简单、数学扩展性好，能够解释多种真实场景下的交通流现象，一经提出便引起了众多学者的关注和研究，而后，在此模型的基础上又进行了一系列的扩展和延伸；Helbing和Tilch为了解决OV模型中存在的加速度过大问题，其利用实测数据对最优速度模型进行了重新标定，提出了广义力模型；姜锐等人通过对跟驰行为的观察，认为由两车相对速度变化所引起的加速度，无论其正负都需要加以考虑，同时还认为跟驰车辆的加速度还与其车头间距的大小有关，继而提出了全速度差(Full Velocity Difference，FVD)模型；孙棣华等人在FVD模型的基础上，考虑后向车辆和速度差对交通流的影响，提出了后向观测速度差(Backward Looking and Velocity Difference，BLVD)模型，通过分析该模型能够有效提升交通流的稳定性。近年来，随着智能交通领域如火如荼的发展，针对车辆网及无人驾驶环境下的跟驰行为受到了广大学者的重视，并由此展开了一系列研究。罗嘉陵以车-车通信为切入点，考虑多前车速度差和协同优化速度，提出了无人驾驶环境下的多信息融合跟驰模型，并且进行了稳定性分析和相应的模拟仿真；纪艺在OVCM模型的基础上提出多前车最优速度与紧邻加速度的跟驰模型，其仿真结果表明改进后的模型可以有效地消散扰动同时能够提高车辆行驶的平稳性。

以上各位学者所提出的模型不仅丰富了微观交通流理论的研究，同时在提高交通流稳定性方面贡献了一份力量。从当前发展趋势来看，未来的交通出行更倾向于智能化和无人驾驶，在此情形下超视距的驾驶成为可能，考虑多前车及后车车头间距下的优化速度、多前车及后车速度差等因素可进一步提升交通流的稳定性。但是这些因素并没有在以上提出的模型中得到综合体现。

为了克服上述模型的不足，以OV模型、FVD模型等为参考依据，同时综合考虑前向多车及后向优化速度、多前车及后车速度差以及传感器敏感度系数等因素，提出了V2V环境下的微观交通流模型，进而推导出了模型的临界稳定条件，同时分析了参数对模型稳定性的影响，最后进行了相应的数值仿真，验证了新改进的模型可以进一步改善交通流的稳定性。

2 模型提出

2.1 模型假设

提出的微观交通流模型是基于V2V正常通信环境下的，即默认车队中所有车辆是无人驾驶的。所以在建立模型时须遵从以下几点假设：

1)传统跟驰模型中驾驶员的灵敏度系数由传感器敏感度系数替代；

2)车队中的车辆均匀行驶在单一的车道中，并且不存在超车及变道行为；

3)车辆在跟驰行驶过程中仅考虑纵向速度、加速度以及位置的变化，不考虑车辆的横向变化；

4)车队中的跟驰车辆可以准确获取其前向多车及后向相邻车的运行数据信息。

V2V环境下车辆跟驰行驶如图1所示。

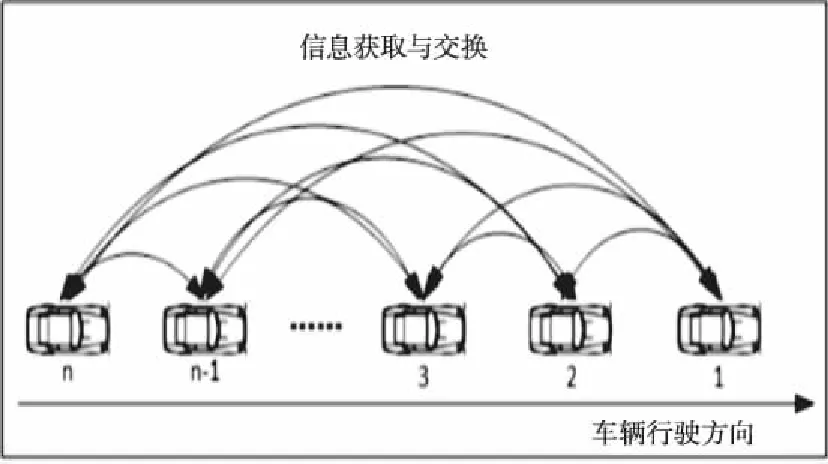
图1 跟驰行为示意图

2.2 模型描述

在V2V通信环境中，车队中的车辆可以获取到多种道路交通运行信息，并且彼此之间可以进行信息的交换。通过上文对相关研究背景的总结与分析后，在车—车建立正常通信的情况下，综合考虑传感器敏感度系数、基于前向与后向的优化速度、多前车及相邻后车速度差以及多前车车头间距，构建基于V2V环境下的微观交通流模型(Vehicle to Vehicle Normal Communication Model，简称V2V-NCM)，模型的基本表达式为

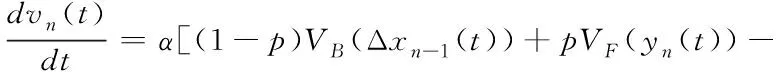
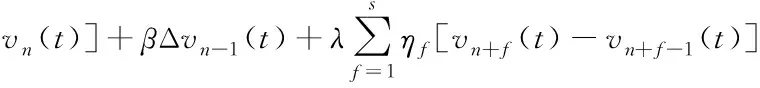
(1)

式中：表示安装于车身上的传感器敏感度系数，>0；表示前向车辆对跟驰车的影响系数，由实际交通状况可知05<≤1；(Δ-1())表示后车的优化速度；(())表示前向多车情形下的优化速度；表示后车速度差的影响系数；表示多前车速度差的影响系数；为前向观测的车辆数；为跟驰车与前辆车速度差的权重系数。同时模型中所采用的最优速度函数形式如下

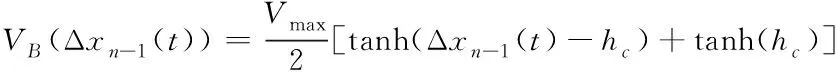
(2)

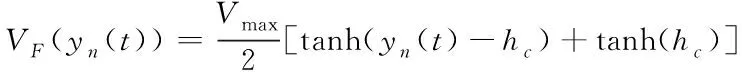
(3)

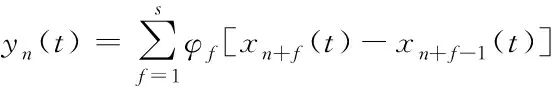
(4)

其中：为自由流时车辆的最大行驶速度；Δ-1()表示跟驰车与其后向相邻车的车头间距；表示跟驰过程的安全距离；()表示前向多车情形下各车头间距的加权值，其中为多前车车头间距对最优速度函数的权重系数，取值如下

(5)

3 稳定性分析

3.1 临界稳定函数

假定车辆数为的车队均匀的行驶在长度为的道路上，车头间距为=，速度为(1-)()+()，加速度为0，默认此时的交通流处于稳态，则稳态下车队中第辆车的位置可以表示为

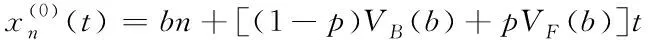
(6)

对车队施加一个扰动()=(-)后，可得

(7)

将式(7)带入模型(1)中，并线性化得

(8)

对方程(8)中的()进行傅里叶级数展开得式(9)

=[(1-)′()(-1)+

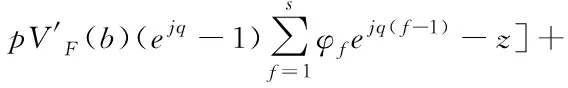
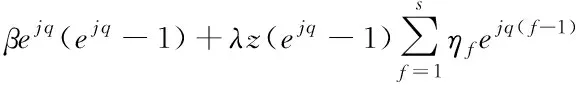
(9)

参数可展开为：=()+()+…，带入方程(9)中可得

(10)

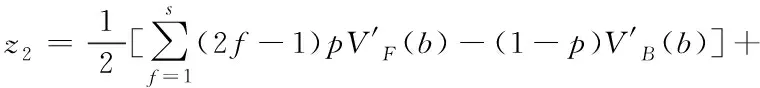
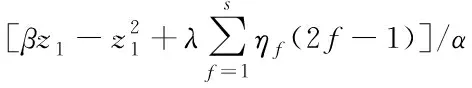
(11)

因此，为使跟驰车队在扰动的影响下仍能保持在稳定状态，则2-模型需要满足以下临界稳定条件

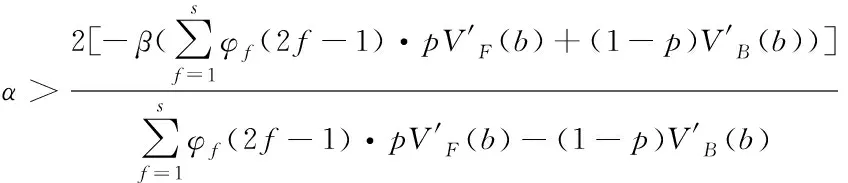
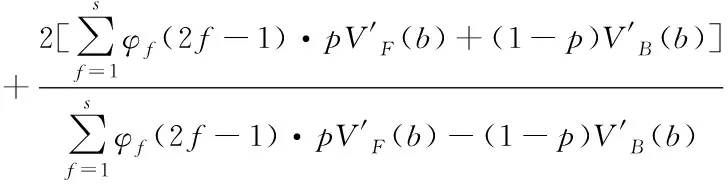
(12)

3.2 模型、参数稳定性分析

当=1，=0，=0且=1，=1时，表示模型中仅考虑前导车与跟驰车辆间的前后车距对跟驰车运行的影响。此时2-模型的临界稳定条件就退化为与模型的稳定性条件一致，即

>2′(Δ())

(13)

当=1，=0，=1且=1时，表示模型中考虑前导车与跟驰车辆间的前后车距和前后车辆的速度差对后车跟驰行为变化的影响，即仅考虑前向第一辆车对跟驰行为的影响，而不考虑后向车辆对跟驰行为的影响。此时2-模型的临界稳定条件就退化为与模型的稳定性条件一致，即：

>2′(Δ())-2

(14)

临界稳定曲线是评价交通流系统模型稳定性的一个重要指标，其是指以车头间距为自变量、传感器灵敏度系数为因变量而建立起的临界稳定函数。通过临界稳定曲线可以直观的看出模型的稳定性情况，即稳定区域范围越大，表明模型的稳定性就越高。图2是模型、模型以及2-模型在不同前向观测车辆数下的临界稳定性曲线对比图。其中参数取值为：车辆最大行驶速度=2，车辆跟驰行驶时的安全间距=35；2-模型(=09，=01，=02，分别取1，2，3)、模型(=1，=0，=0，且=1，=1)、模型(=1，=0，且=1，=1)]。

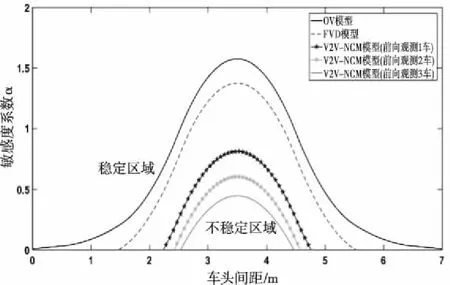
图2 模型临界稳定曲线对比图

图2中的曲线便是各个模型所对应的临界稳定曲线。临界稳定曲线以上部分为模型的稳定区域，曲线以下部分则为模型的不稳定区域。从图2中可以直观的看出OV模型、FVD模型以及V2V-NCM模型的临界稳定曲线依次减小，即各模型的稳定区域依次增大。在V2V环境下构建车辆跟驰模型时考虑的因素越全面，交通流系统的抗扰性就越强，模型的稳定性显著高于其它模型。

模型中某些参数的变化会对其自身的稳定性产生一定的影响，即参数的取值不同、模型的稳定区域也不尽相同。根据相关参考文献[20，21]中的取值，针对模型中的参数变化对其稳定性的影响进行分析。图3分别展示了模型中参数、、对系统稳定性的影响。从图中可以看出，当其余两个参数固定时，模型的稳定区域随参数值的增大而减小。因此，在车-车通信情况下更多关注前车的运行状态、相邻后车的速度以及多前车速度差等因素后，使得车辆在跟驰过程中有了更大的稳定行驶空间，即在该模型下交通流系统的稳定性得到了有效地改善。

图3 参数p、β、λ对模型稳定性的影响

4 数值仿真验证

上文中对模型的稳定性以及参数取值对模型稳定性的影响进行了理论分析，为了对分析结果作进一步验证，在周期性边界条件下基于Matlab软件对改进模型进行数值模拟仿真验证分析。

设定仿真初始条件为：模拟车辆数N=100，模拟道路长度L=500m，且所有模拟车辆均以相同的车头间距==5均匀的分布在道路上。传感器敏感度系数参照相关文献[22]标定结果的范围取12；其余参数，，的取值根据上文的影响结果分析以及相关文献[23]中的研究结论，依次取值为：09、01、02；跟驰过程中车辆间的安全距离及车辆最大行驶速度的取值与上文相同，在此初始条件下进行数值仿真验证。

4.1 交通扰动过程仿真分析

为了验证V2V-NCM模型的抗扰性，在上述设置的初始条件下，给处于稳态下的交通流施加扰动，得到不同时间条件下车队中所有车辆的速度分布图，如图4所示。

图4 不同时刻下车辆速度分布

图(a)～(c)中车辆的速度大致围绕1.9033m/s这一稳态数值上下波动，其波动幅度较小，表明车队在受到扰动后仍能保持一个较为稳定的行驶速度；在1000s时车辆均以稳态速度行驶，说明经过系统自身的调节，施加的扰动能够在车队的运行过程中逐渐消散，使其重新恢复到稳定状态。

4.2 车队启动过程仿真分析

车队启动过程仿真参数与上文一致，在初始时刻下头车启动后，其余车辆依次跟随启动行驶。选取车队中连续的10辆车作为研究对象，得到仿真结果如图5所示。

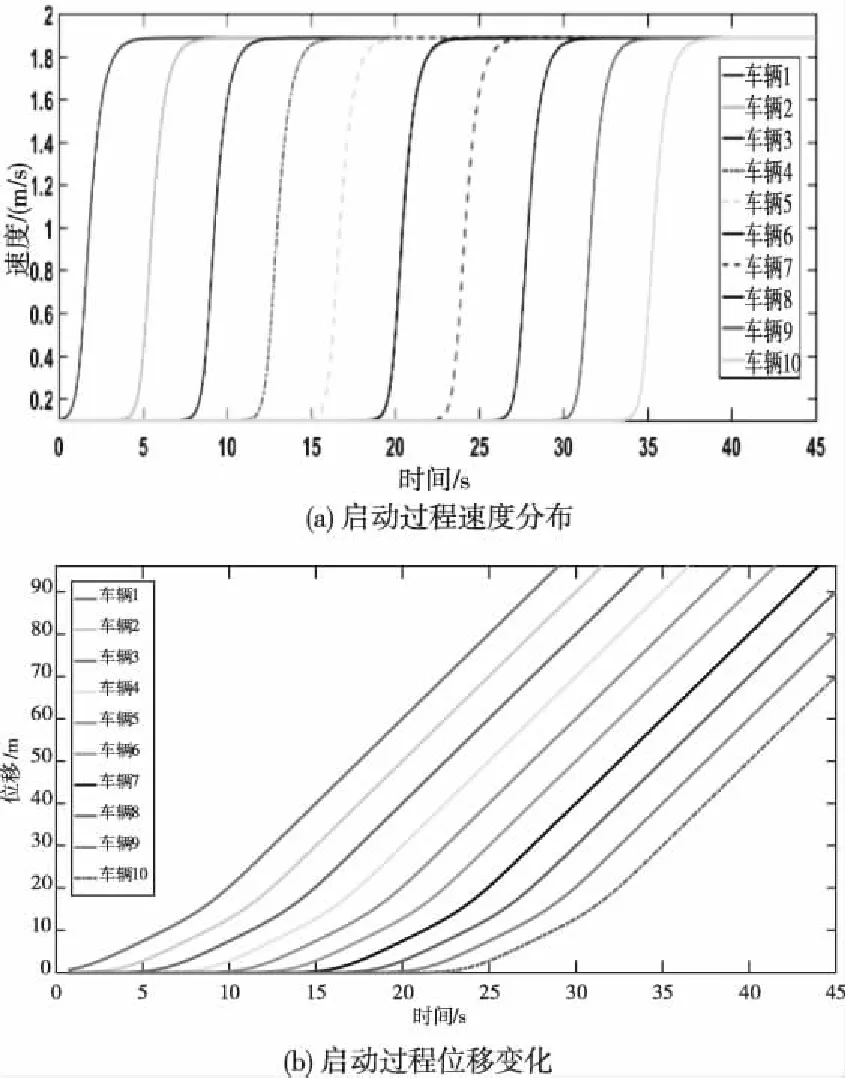
图5 车队启动过程中速度、位移变化

由图(a)可知，车辆在较短时间内达到稳态速度，且跟驰车在5s内便能够赶上其前导车的速度同时不存在较大波动，说明V2V-NCM模型其启动时间较快，可在较短的时间内达到最优行驶速度，符合实际驾驶行为；此外，图(b)中各车辆位移持续平稳增长且未呈现出波动现象，表明车队在启动时交通流能够以平稳的速度运行，具有较好的稳定性。

4.3 车队停止过程仿真分析

车队停止过程仿真参数与上文一致，设定在距头车前方90m处存在停止线，需车队由匀速状态逐渐减速至停止状态。其仿真结果如图6所示。

图6 车队停止过程中速度、位置变化

从图(a)中可以看出，车辆能够在较短的时间内完成从稳态速度减速至停止状态的过程，且不存在速度的波动，表明在V2V环境下相邻车辆对各自彼此间运行变化的操作反应比较及时，对交通流运行的影响微乎其微。此外，由图(b)可知车队中各车辆的位置在20s内稳步变化至不再增加，表明模型中的车队可以在较短时间内实现匀速行驶车队的平稳停止。

由以上的分析结果可知：V2V-NCM模型中考虑了多前车车头间距下的优化速度、多前车速度差以及相邻后对跟驰车辆的影响后，车辆可以及时、准确地获取其前后相邻多车的运行状态，因此可以根据所提供的信息事先调整自身车辆的运行行为，通过采取相应的措施来使整个交通流系统保持在一个相对稳定的状态，避免因为扰动的传播而使稳态交通流演变为拥堵流。

5 结论

在传统跟驰模型的基础上，综合考虑了相邻后车及多前车效应下的优化速度和速度差，提出了V2V-NCM跟驰模型。利用线性稳定性的分析方法证明了改进后模型的稳定区域较之于OV模型、FVD模型等有所扩大，模型中的车辆能在较大范围内平稳行驶。通过数值仿真验证了车辆在启动、停止以及受到扰动时的运行情况，结果显示模型具有较强的抗扰性，在上述3种情形下均能有效跟驰且平稳运行，说明在跟驰过程中前后车速度差和车头间距等因素在交通流自身演变过程中可以提高系统的稳定性，进一步证实了V2V-NCM模型能够有效改善交通流的稳定性。另外，由于实际交通状况的复杂性，文中的模型仅考虑了V2V-NCM正常通信情况下的现象，进一步的研究需要考虑实际交通状况下的其它不确定性因素。