基于改进STA的含风电场电力系统动态经济调度

王鹏鲲，王 聪，张宏立

(新疆大学电气工程学院，新疆 乌鲁木齐 830047)

1 引言

在全球节能减排的背景下，风电以其无污染、投入成本低、技术成熟的优点受到了世界各国的高度重视。然而，风电出力具有随机性、间歇性和波动性的特点，大规模风电并网给电力系统的安全稳定运行带来了严峻的挑战。因此，研究含风电场电力系统动态经济调度问题具有重大意义。

动态经济调度(Dynamic Economic Dispatch，DED)是在充分考虑调度周期内各时间段机组耦合关系和约束条件的前提下，确定发电机组输出功率的最优组合，以最小化发电成本。含风电场电力系统动态经济调度需在DED问题的基础上考虑风电的不确定性，因此在建模和求解上更为复杂。

许多传统方法曾被用于解决DED问题。Fu等人使用内点法(Interior Point Method，IPM)对DED问题进行求解，但是因为IPM不适用于非凸优化问题，只能忽略成本函数中机组阀点效应的影响；Ross等人使用动态规划的方法对DED问题进行求解，虽然动态规划能求解非凸问题，但其缺点是随着机组维数的增加，计算所需时间呈指数级增长。为克服传统方法的缺点，更有效地处理具有复杂约束和非线性特征的DED问题，越来越多的学者开始采用智能算法对这一问题进行求解。如改进的径向移动算法(IRMO)、改进的细菌群体趋药性算法(IBCC)、基于分解的多目标进化算法(IMOEA/D-CH)和基于记忆的全局差分进化算法(MGDE)。这些算法均能有效解决不同类型的DED问题，但仍存在算法运行时间长、无法找到全局最优解的缺点。

周晓君等于2012年提出了一种新型随机性全局优化方法——状态转移算法(State Transition Algorithm，STA)，并成功应用于诸多领域。薛永飞等人提出了一种基于改进状态转移算法的串级平推流反应器动力学参数估计方法，有效节约了计算时间；王聪等人将改进的状态转移算法用于混沌电力系统的参数辨识，并取得了很高的辨识精度。但这些文献也表明STA具有易早熟，后期收敛速度慢的特点。本文针对上述问题，建立了考虑成本中阀点效应影响和风电正负旋转备用约束的含风电场电力系统动态经济调度数学模型，使用一种新型的处理约束的修复方法配合罚函数对约束条件进行处理，并在STA的基础上提出了一种基于镜像变换和动态坐标变换的状态转移算法(MTSTA)用于求解此问题。通过对两个经典算例进行仿真，并与其它算法进行对比，结果表明MTSTA具有更快的收敛速度和更高的寻优精度，验证了模型的合理性和MTSTA的有效性。

2 含风电场的动态经济调度模型

2.1 目标函数

电力系统动态经济调度的目标就是在固定时间内，保证各机组满足约束条件，并使发电成本最小。当不考虑风力发电成本，只考虑火电机组燃料成本和阀点效应成本时，发电成本目标函数为

(1)

式中：()为发电机组总运行成本，(，)为发电机组燃料成本；(，)为发电机组阀点效应成本；为调度总时长；为火电机组数量。

(2)

(，)=|sin[(，min-，)]|

(3)

式中：、、为第台火电机燃料成本系数；、为第台火电机阀点效应成本系数；，为第台火力发电机在时间段输出的功率；，为第台火力发电机输出功率下限。

2.2 约束条件

221 系统功率平衡约束

功率平衡约束为等式约束，以保证机组总发电量等于系统负荷加网损之和，表示为

(4)

式中：，、，为时间段第台发电机组输出功率和风电场输出功率，，、，为时间段系统的负荷和网损，，用系数法计算如式(5)

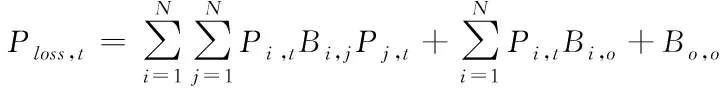
(5)

式中：，、，、，为网损系数；，、，为间段内第、台发电机组的输出功率。

222 机组爬坡速率约束

为保证电力系统稳定运行，每台发电机相邻时间段上升或下降的最大功率是有限的

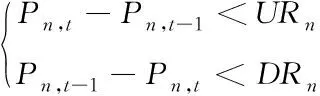
(6)

式中：、为第台发电机单位时间内上升和下降的最大功率。

223 机组功率上下限约束

火电机组出力应受其上下限约束

，min<，<，max

(7)

式中：，、，为第台发电机组的最大输出功率和最小输出功率。

224 系统旋转备用容量约束

风电并网后，由于风电预测的误差较大，综合考虑风电出力的随机性及系统负荷预测的误差，需准备充足的正负旋转备用容量以保证电力系统安全稳定的运行。

系统正旋转备用容量约束

(8)

系统负旋转备用容量约束

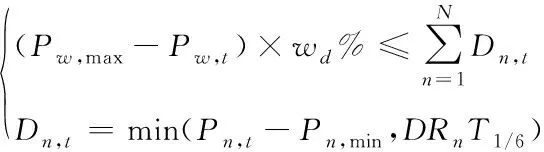
(9)

式中：、为风电预测误差对正负旋转备用容量的需求系数；为系统负荷预测误差对正旋转备用容量的需求系数；，为风电场额定功率；16为旋转备用响应时间，本文取值为16小时。

3 镜像状态转移算法

3.1 状态转移算法

是由周晓君等人于2012年提出的一种新型的随机性全局优化方法。具有搜索能力强、收敛速度快的特点，广泛地应用于各类优化问题的求解，并取得了很好的效果。

基本的状态转移算法包含以下四种算子

1)旋转变换(Rotation Transformation，RT)

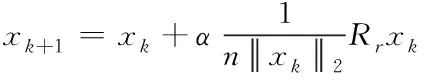
(10)

其中：>0为旋转因子；∈×是一个元素取值在[-1，1]之间均匀分布的随机矩阵；‖·‖为向量2范数。旋转变换具有在以为半径的超球体内进行搜索的功能。

2)平移变换(Translation Transformation，TT)

(11)

其中：>0为平移因子；∈是一个元素取值在[0，1]之间均匀分布的随机数。平移变换是一种线搜索，它以为起点，指向-1的方向，搜索的最大长度为。

3)伸缩变换(Expansion Transformation，ET)

+1=+

(12)

其中：>0为伸缩因子；∈×是一个非零元素取值服从高斯分布的随机对角阵。伸缩变换能够把中的每一个元素伸缩到整个坐标空间中。

4)坐标变换(Axesion Transformation，AT)

+1=+

(13)

其中：>0为坐标因子；∈×为服从高斯分布的稀疏随机对角阵，且仅有一个随机位置为非零值。坐标变换的功能是增强单一维度的搜索。

3.2 镜像变换(Mirror Transformation，MT)

为提高状态变换的搜索能力，丰富候选解多样性，本文提出一种新的算子——镜像变换。

即每次状态变换后，将候选解集=[，，…，]划分为位置上下对称的两个矩阵=[，，…，2]和=[2+1，2+2，…，]。随机选取矩阵的一列向量：，，将和矩阵以此列向量：，为分界的后半部分矩阵进行镜像对称。其示意图如图1所示。

图1 镜像变换示意图

镜像变换极大地丰富了候选解的多样性。将镜像变换后的候选解与原候选解合并，从中选出新一代最优解，更有利于找到全局最优解。

3.3 动态坐标变换

伸缩变换虽然能保证算法的全局搜索能力，但在求解本文问题时，由于每次变换改变的维度太多，很难满足约束条件。所以本文将伸缩变换与坐标变换结合起来，提出了一种动态坐标变换。动态坐标变换与原本的坐标变换相比，其搜索维度会根据迭代次数不断变化，使算法在搜索前期偏重于全局搜索，快速定位较优解的分布区域，加快算法收敛速度；搜索后期偏重于局部搜索，进一步提高解的质量。动态坐标变换很好的兼顾了算法的全局和局部搜索能力，其搜索维度满足以下公式

(14)

式中是搜索维度，是最大迭代次数。

4 含风电场DED问题模型求解

4.1 处理约束的修复方法

含风电场DED问题具有高维度多约束的特点，为保证MTSTA每次状态变换后产生的候选解均在可行域内，本文在处理约束条件时采用了一种新型的处理约束的修复方法，具体步骤如下：

Step1：将约束条件(6)和(7)合并为下式：

min(，max，，-1+)≠1

(15)

Step2：对于每一个决策变量，(=1，2，…，；=1，2，…，)，若违反约束条件(15)便直接让其等于边界值，经过这一步骤所有的决策变量便均满足约束条件(6)和(7)。

Step3：对于调度周期的每一时间段，均随机从个电机中选择一个发电机，并将其数值变为待定状态，另外-1个发电机与此发电机共同满足约束条件(4)，如下式所示：

(16)

可以看出式(16)为关于发电机，的一元二次方程。求解此方程，若有解便可以得到，的值并结束，否则转至Step4。

Step4：当方程无解时，重新从N个电机中选择一个不同于m的发电机转至Step3，当没有未选择过的发电机时转至Step5。

Step5：经过前四个步骤后绝大多数决策变量均满足约束条件，对于极少数不满足约束条件的决策变量用罚函数的方法进行处理，约束违反度函数与目标函数共同构成的惩罚函数如下

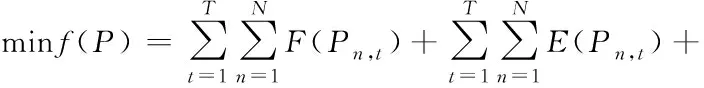
(17)

式中为惩罚因子，、是旋转备用容量违反度。

4.2 MTSTA在含风电场DED问题中的应用

在MTSTA中，个体在搜索空间的位置对应经济调度问题中火电机组各时段的输出功率，，个体维度由机组数量和调度时间段的乘积所确定。将发电成本作为目标函数，所有约束条件构成约束违反度函数。求解含风电场电力系统动态经济调度问题的流程图如图2所示，具体步骤如下：

Step1：设置镜像状态转移算法中各参数大小，进行候选解随机初始化。

Step2：对初始化后的候选解进行约束修复处理，计算候选解中个体的适应度值，从中选出初始最优个体gbest。

Step3：对初始最优个体进行旋转变换、镜像变换和平移变换，且每一次状态变换后均进行约束修复处理。

Step4：根据迭代次数选择坐标变换维度进行动态坐标变换，计算适应度值得到新一代最优解。

Step5：判断是否满足最大迭代次数，若满足，结束并输出结果；否则，g=g+1转至step3。

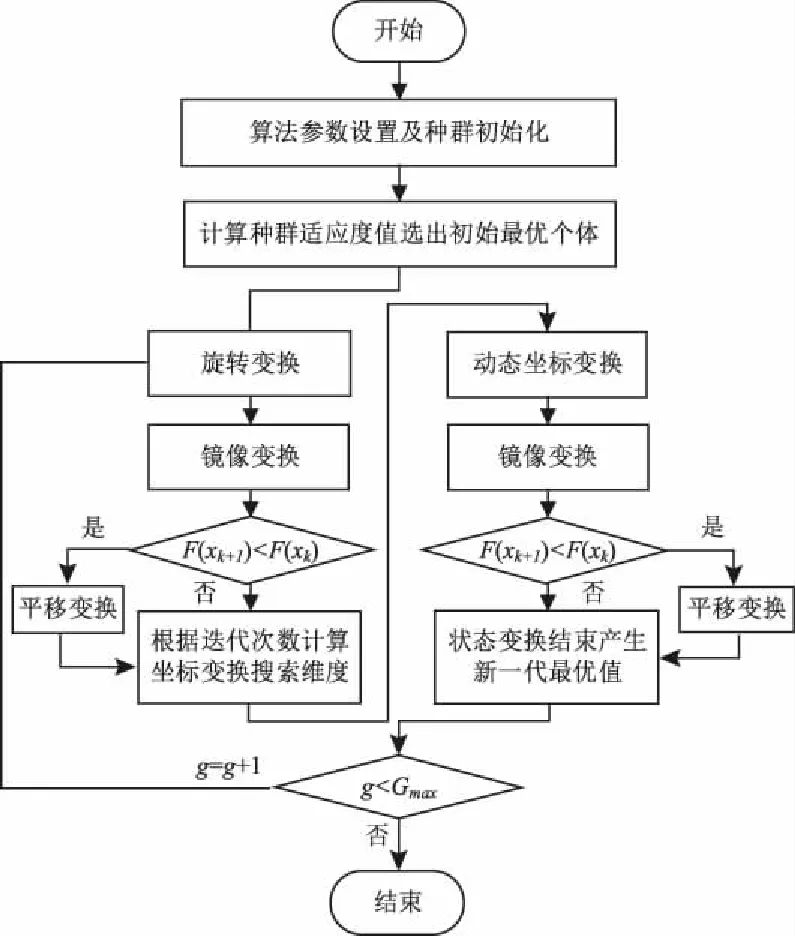
图2 MTSTA流程图

5 算例仿真与分析

为验证模型的合理性和MTSTA求解含风电场电力系统动态经济调度问题的良好性及快速性，以10机系统(调度周期24h，时间间隔1h)为例进行仿真。每台发电机的物理特性参数，各时段的系统负荷预测值，网损系数均来自文献[15]。

5.1 无风电10机系统仿真

首先，在无风电并网情况下对算例进行仿真。MTSTA和STA的各参数设置如下：搜索范围SE=30；最大迭代次数G=200；惩罚因子ζ=10；旋转因子α=50→10；平移因子β=50；坐标因子δ=50；伸缩因子γ=50。

图3 无风电情况下两种算法的适应度曲线

图4 无风电情况下两种算法30次的运行结果

图3为MTSTA与STA的成本适应度曲线。可见，MTSTA在整个迭代过程中的收敛速度和寻优精度均要优于STA。为避免一次实验结果的偶然性，将MTSTA与STA各自运行30次，寻优结果如图4所示，进一步验证了算法改进的合理性。

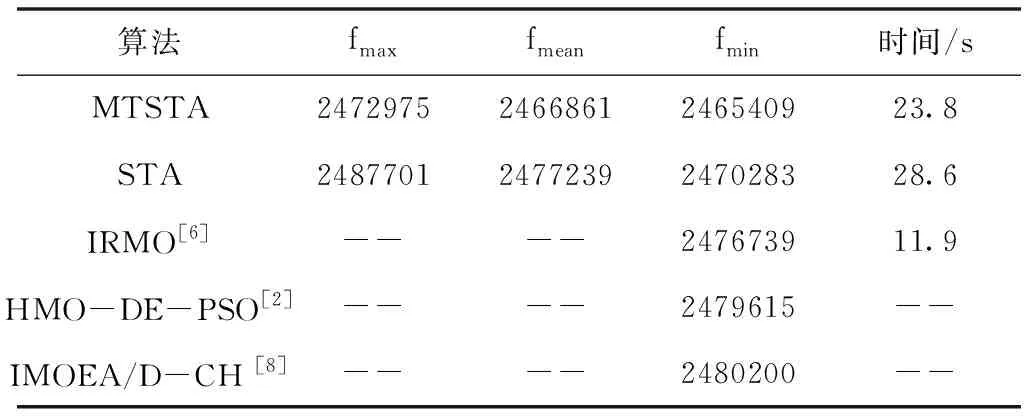
表1 无风电情况下各算法运行30次结果统计

表1为MTSTA与其它几种算法的对比结果。由于求解含风电场DED问题的相关文献大多是多目标优化架构，故文献[2]和文献[8]的比较数据为其Pareto前沿的成本最优解。相较于IRMO算法，虽然MTSTA运行时间更长，但是MTSTA的结果比其减少了11330美元。与其它算法相比，MTSTA在收敛速度和寻优精度方面均表现出较优性能。

5.2 含风电10机系统仿真

现考虑含风电场并网发电的情况，在10机系统中加入一座额定功率为100MW的风电场，再次进行仿真。其中，风功率预测值见表2，、的取值分别为02和03，取值为002，最大迭代次数=500，其余各参数与之前保持一致。

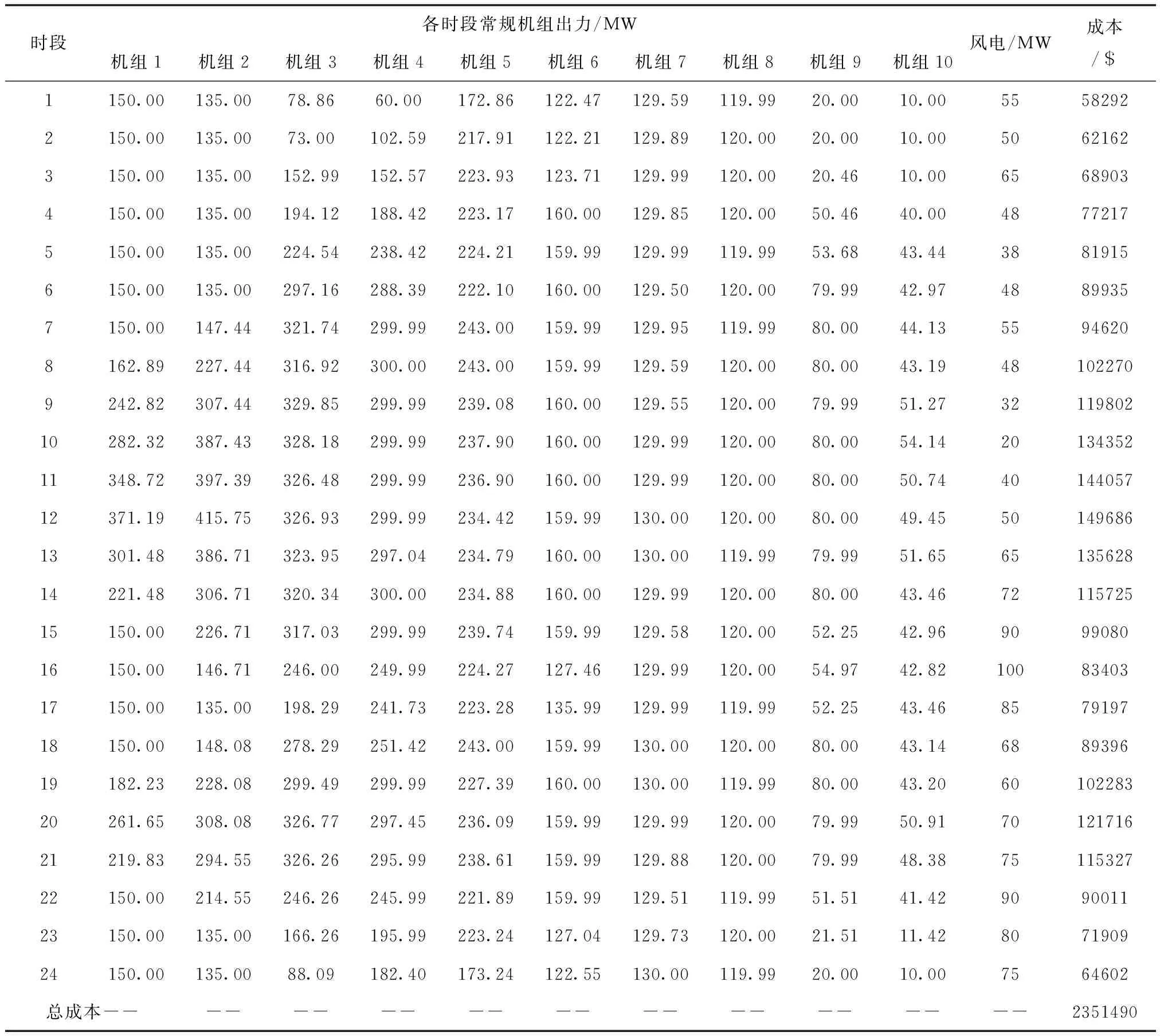
表2 含风电场10机系统各时段机组出力及成本

图5为MTSTA与STA分别迭代500次的成本适应度曲线。表2给出了MTSTA运行30次的成本最优解及各机组具体出力值。

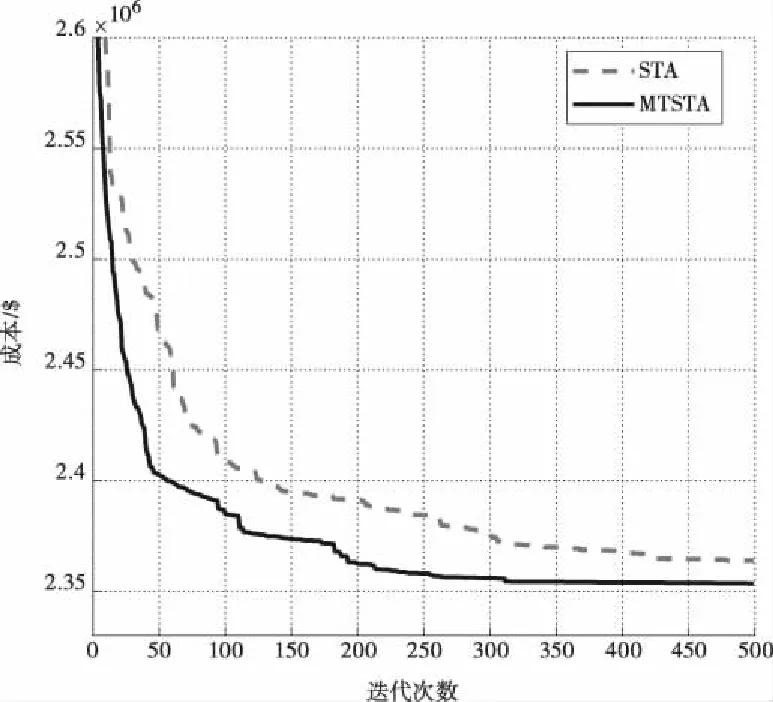
图5 两种算法的适应度曲线

图6为所有发电机组在整个调度周期内各时间段的运行情况及系统的网损、负荷。该图验证了MTSTA的所求结果完全满足系统功率平衡约束。

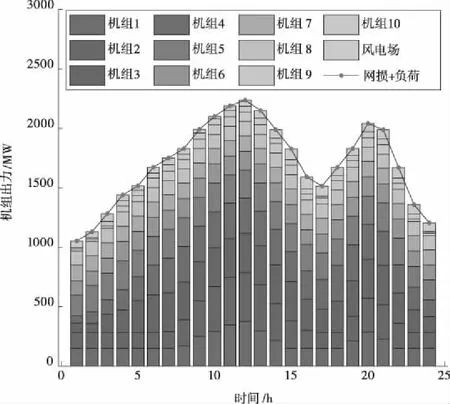
图6 调度周期内各机组出力

将MTSTA与其它几种算法进行对比，迭代次数增加到1500次。图7可以看出相较于其它算法，MTSTA在迭代500次左右便找到较优值，且优于其它算法迭代1500次的结果。

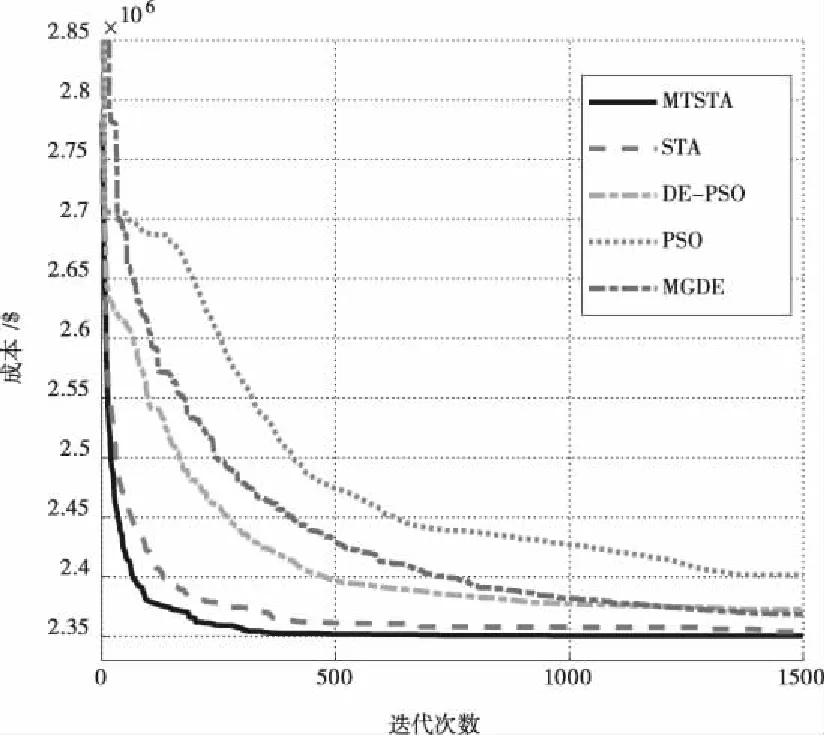
图7 MTSTA与对比算法的适应度曲线

表3给出了MTSTA与其它几种算法的对比结果。由于收敛速度差距较大，MTSTA、STA取迭代500次后的结果，DE-PSO、MGDE分别取迭代1500次和3000次的结果(MGDE在文献[9]中用于求解其它DED问题数学模型)。MTSTA与MGDE算法相比，MGDE算法拥有更高的稳定性，故平均值较MTSTA低591美元，但MTSTA比其运行时间少92.5秒，最优成本也低2247美元。MTSTA相较于其它算法在收敛速度和寻优精度方面均表现出较优性能。

表3 各算法运行30次结果统计

同时，通过对比有无风电场电力系统的发电成本可以发现。风电并网前平均发电成本为2466861美元，风电并网后平均发电成本为2355258美元，比之前下降了111603美元。可见，风电并网对降低系统发电成本是有利的，同时也验证了模型的合理性。

6 结论

本文针对含风电场电力系统动态经济调度问题，提出了一种基于镜像变换和动态坐标变换的状态转移算法进行求解。首先，为处理风电的随机性，在约束条件中考虑正负旋转备用容量，建立了含风电场电力系统动态经济调度的数学模型；其次，在STA的基础上加入了镜像变换和动态坐标变换，丰富了候选解的多样性，提高了算法的收敛速度和寻优精度；最后，用含一座风电场的10机系统作为算例进行仿真，并与其它采用相同算例的文献进行对比。实验结果验证了模型的合理性及MTSTA的有效性。本文为求解含风电场电力系统动态经济调度问题提供了一个新的可行方案。