基于高维统计学习的能源网需求响应仿真研究

付一木，郑志杰，孙东磊，贾倩倩

(国网山东省电力公司经济技术研究院，山东 济南 250021)

1 引言

综合能源系统(Integrated Energy System，IES)由冷、热、电、气相关的多种能源、能量网、储能设备和终端用户组成。在IES 下，各类能源转换设备如热电联产机组(Combined Heat and Power，CHP)、电热锅炉和燃气锅炉等使电力、热力和天然之间紧密耦合，实现了多能源的互动及转换。由电力系统、供热供冷系统和天然气系统等构成的IES使得能量利用更加高效、环保和经济。IES理论和技术的发展有助于帮助解决能源安全问题，提高社会效率，促进新能源和可再生能源的发展。

目前，对于传统需求响应(Demand response，DR)策略的研究已有较多研究成果。文献[3]以分布式光伏消纳最大化作为优化目标，制定负荷的需求响应方案。文献[4]通过对温控负荷进行合理的建模，使用户参与电网调峰过程。文献[5]针对智慧园区的集成特性，提出双层优化调度模型，实现负荷主动参与系统运行。文献[6]分析了价格激励信号对企业需求响应行为的影响。

现有研究虽然通过不同的优化目标制定相应的需求响应方案，但是没有考虑天气因素的不确定性对高质量的DR负荷——温控负荷的影响。天气因素之间的相关性使得分布式光伏电源等间歇性分布式能源和热负荷之间具有一定的相关关系。此外，光照、温度和风速是计算建筑物供暖负荷的主要因素，而建筑物供暖系统与分布式光伏电源之间有着复杂的线性或非线性相关关系。因此天气因素能够影响IES的响应策略，有必要对其进行研究。确定性的潮流(Deterministic Power Flow，DPF)已不适用于具有不确定性的IES分析，概率潮流(Probabilistic Power Flow，PPF)成为IES、电力系统不确定性优化的重要依据。

以往使用蒙特卡罗法、解析法和近似法等数值模型在高维样本情况下计算PPF时复杂度较高，耗时长。回归模型成为解决复杂系统难以建模、计算复杂度高等问题的新手段。然而回归模型在处理高维样本时同样面临着“维数灾难”、“过拟合”的难题。本文提出了一种基于统计机器学习方法中的主成分分析法(Principal Component Analysis，PCA)和随机响应面模型(Stochastic Response Surface Model，SRSM)的PPF快速计算方法，记为PSRSM(PCA and SRSM，PSRSM)。首先通过降维方法削减样本数据的维数，再使用回归模型将低维数据拟合，用于求解分析综合能源概率潮流，得到准确的光伏并网电压、总燃气消耗、热电联产系统负荷率的概率特征，最终得出优质需求响应结果。

综上，本文提出的基于高维数据统计学习的综合能源系统动态需求响应策略研究，包括三部分：首先通过华东某地真实历史天气仿真出温度、光照等天气数据；其次将物理建模得到的光伏出力和热力负荷高维数据作为PSRSM模型的输入样本，光伏并网电压、总天然气消耗、CHP系统负荷率的概率特征分别作为响应量进行拟合；最后分析不同室内温度控制下响应量的关系，综合考虑经济性和安全性后制定出响应策略。本文后续章节安排如下：第二章介绍了考虑天气不确定性的能源网需求响应模型；第三章提出了一种名为PSRSM的PPF快速计算方法；第四章仿真通过构建的IES实例验证了所提方法的有效性，并得出经济性与安全性并存的动态响应策略。

2 能源网需求响应建模

本章将简要介绍用于仿真天气数据样本和多能概率潮流响应量的各个模型，为仿真数据的真实性提供坚实基础。

2.1 天气模型

假设太阳光照辐射的概率分布函数(Probability Distribution Functions，PDFs)与文献[10]中的Beta分布相同

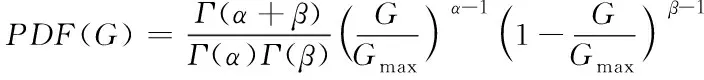
(1)

式中是伽马数学函数，和是其形状参数，和分别是当前和最大太阳辐射值。

假设室外温度的PDF为正态分布

(2)

式中，为室外温度，和分别是其均值和标准差。

使用Copula函数表示光照与温度之间的相关关系，二者的边际累积概率分布(Cumulative Distribution Functions，CDFs)为

=(()，()，)

(3)

式中(·)为累积分布函数，(·)为一个函数的，为线性相关参数的矩阵。

2.2 光伏有功功率模型

光伏发电系统的有功输出功率模型为

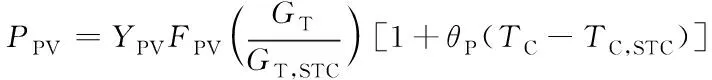
(4)

式中，是标准测试条件下的电池温度，为25℃；为光伏板的额定容量；为光伏系统的功率降额因子；是当前太阳光照强度，是在标准测试条件下的太阳光照强度，单位是；是光伏电池功率的固有温度系数。

另外，光伏电池当前温度计算为

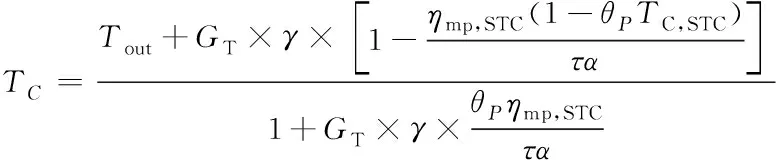
(5)

式中，为室外环境温度；为标准测试条件下的额定电池温度；是标准测试条件下的最大功率点效率；为已知常数。

2.3 热负荷模型

本文以华东某地建筑冬季供暖负荷为例，冬季供暖负荷主要受温度的影响。冬季外墙和屋面的供热负荷可计算为

(6)

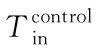
外窗的热负荷可计算为

(7)

式中，={1，2，3，4}分别代表东窗、南窗、西窗、北窗；为窗户的传热系数；为窗户面积。

冬季新风采暖负荷可计算为

=(-)

(8)

式中，为一人新鲜空气的体积；为人数；为空气的密度；为供暖季新鲜空气的定压比热容；表示当前室内温度。

因此总的供暖热力负荷为

=++

(9)

从上述公式可以看出，光伏发电的有功功率与太阳光照强度具有函数关系，供暖热力负荷与室外温度具有函数关系，因此可以将天气的不确定性转移到光伏出力和热力负荷中，作为PSRSM模型的原始输入样本。

2.4 IES模型

水力模型电力系统模型，与文献[14]一致，本文不再赘述。与所研究需求响应策略密切相关的IES的热网、CHP和天然气网络模型描述如下。

首先，热力网络模型描述如下

(10)

式中，表示热力网络的节点热功率，为水的比热容，和分别表示每热负荷节点的供热温度和输出温度；与分别代表管道末端和初端的温度，为环境温度，是管道的热传导系数，是管道的长度；、和、分别是流入和流出管道中睡得流量和温度。

其次，燃气轮机驱动的模型中电功率、热功率的关系为

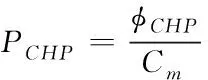
(11)

的耗气量可由式(12)求得

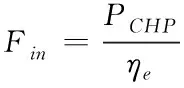
(12)

式中，为机组的热电比例系数；与所发出的电功率有关，本文假设其为常数。

带压缩机的天然气管道的稳态流量可以用式(13)计算

(13)

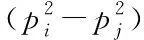
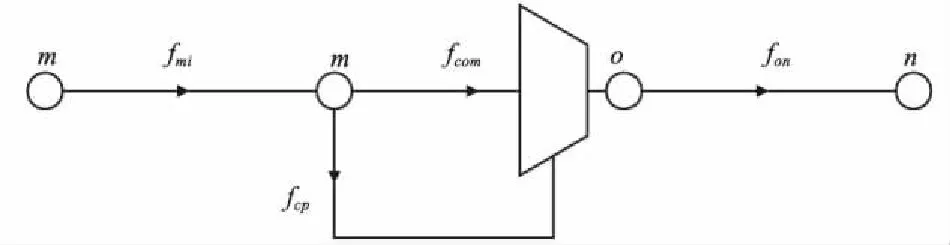
图1 含燃气轮机驱动的压缩机的管道

由燃气轮机驱动压缩机的管道模型如图1所示，，分别为流过压缩机的流量和出口管道的流量，为压缩机消耗的天然气量，为压缩机入口管道的流量。数学表达式可以描述为

(14)

式中，为压缩比；、为入口管道和出口管道的管道常数；、、、为图1 中4 个节点的压力；为天然气热值；为天然气温度；为多变指数。

3 需求响应策略

本章介绍了制定需求响应策略的具体过程和影响因素，并在策略调整的计算环节提出了一种名为PSRSM的PPF快速计算方法，使用第二章中生成的光伏出力与热力负荷样本作为输入样本，多能概率潮流作为输出响应量，进行回归拟合后得到多个多能概率潮流的概率特征值，为制定需求响应策略提供辅助决策信息。

3.1 PSRSM方法

本小节提出了一种名为PSRSM的PPF快速计算方法，用于策略调整的计算环节，具体过程如图2所示。

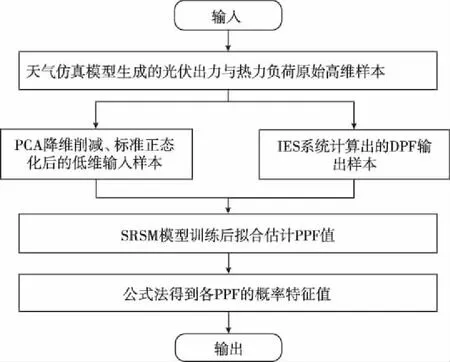
图2 PSRSM方法流程图

3.1.1 PCA降维削减

高维输入样本会增加回归模型的计算复杂度，产生模型过拟合问题。因此需要对输入样本进行降维削减。PCA是一种基于最大方差理论的典型线性降维方法，从线性代数的角度分析，其意义在于使用另一组基来重新描述得到的数据空间。具体步骤如下：

步骤一：对原始输入样本矩阵进行去中心化处理；

步骤二：求取去中心化后样本矩阵的协方差矩阵，并求取特征值和其对应的特征向量；

步骤三：将特征值由大到小排列，根据方差贡献率特征值；

步骤四：被选特征值所对应的特征向量即为降维后的低维样本矩阵；

PCA通过向量与矩阵运算将样本投影至低维空间中实现降维，计算过程不涉及寻优。原始特征集中有共同特点的特征会被投影到同一主轴方向，代表一个低维维度。

3.1.2 SRSM回归拟合

SRSM是一种基于Hermite多项式的显式多项式混沌展开

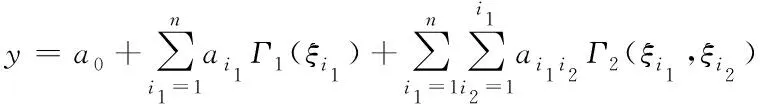
(15)

式中，，，和是标准正态分布变量；为响应向量，表示状态变量；(·)表示阶的多维埃尔米特多项式；是一个未知的确定性系数，需要估计。式(15)的逼近精度取决于多项式的阶数，待定系数的个数为

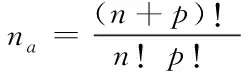
(16)

样本容量为

=2×

(17)

通过最小化残差的合适范数来确定多项式混沌展开中的未知系数，并利用最小二乘法构造曲面。需要注意的是，输入变量的样本个数是待定系数个数的两倍。

313 基于PSRSM的PPF快速计算方法

本文在需求响应的策略调整的计算环节提出了一种名为PSRSM的PPF快速计算方法，首先通过PCA降维算法对数据进行维数削减，再通过统计机器学习的SRSM方法进行PPF快速计算。

在本文中，进行降维处理的是仿真生成的光伏出力与热力负荷组成的原始输入样本，其中式(15)的输入样本，，和表示将原始输入样本经过降维削减和标准正态化处理后获得的低维样本；输入变量的样本个数为

=

(18)

其对应的输出响应向量是通过IES模型计算得到的各个多能概率潮流。当输入规模远远小于实际场景数量时，很明显可以提高PPF的计算速度。

本文引入二阶SRSM来估计PPF，利用该方法可以计算响应向量的数字特性

()=

(19)

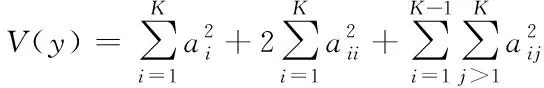
(20)

其中E(·)是SRSM的数学期望函数，V(·)是SRSM的方差函数。通过计算系数，不仅可以得到概率数字特征，而且可以用式(15)得到与一组输入向量相对应的响应变量。

本文提出的PSRSM方法使用PCA减少样本维数，使用SRSM来减少场景数量，即样本个数来减小DPF的计算复杂度，其目的是减少PPF时间成本。

由式(15)可知，维数越高，公式中的项数越多，计算过程就越复杂。但是需要注意的是，根据式(16)，考虑到降维和SRSM的时间代价，使用SRSM计算PPF的前提是SRSM系数的数量小于原始样本量的一半。

SRSM的作用是准确快速计算出不同室内温度设置值下的能源系统运行的概率特征(温度下降带来燃气消耗下降，但是究竟能下降多少，多大空间，需要本文方法计算)，量化结果为需求响应策略制定依据。

3.2 热负荷需求响应方法与过程

热负荷是优质的需求响应资源，而室内控制温度是影响供暖热力负荷的关键因素。

(21)

总的供暖热力负荷更新为

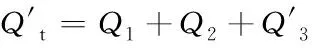
(22)

那么需求响应的公式为

(23)

式中，Q表示为达到设定的室内温度所需热负荷与之前室内温度所需热负荷的差值，具体的热负荷需求响应过程如图3所示。

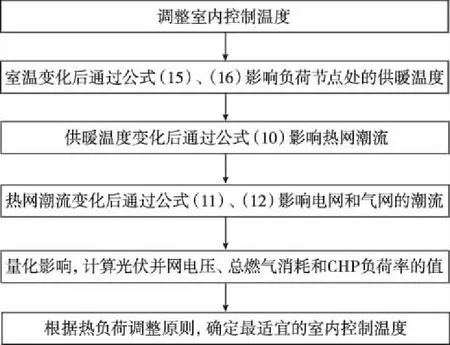
图3 热负荷需求响应过程

图3中，热负荷调控的原则为，在适宜的温度范围内，让整个综合能源系统的经济性和安全性最优。其中经济性体现在天然气消耗小、发电负荷率大；安全性体现在光伏电压偏差小。

4 实例仿真

4.1 IES系统构建

本文以典型电、热、气系统网络为研究对象，如图4所示。仿真中使用的电力系统、热力系统和天然气系统的主要参数如表1—表3所示。第4、7、8和10节点为光伏接入点，设立电网管理站、天然气管理站和IES管理站保障系统安全运行。

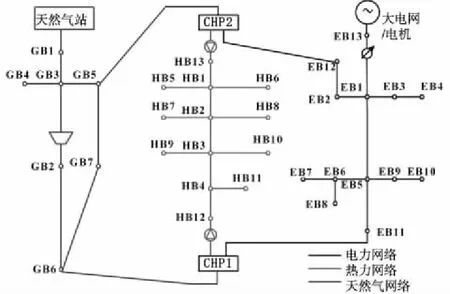
图4 IES结构图

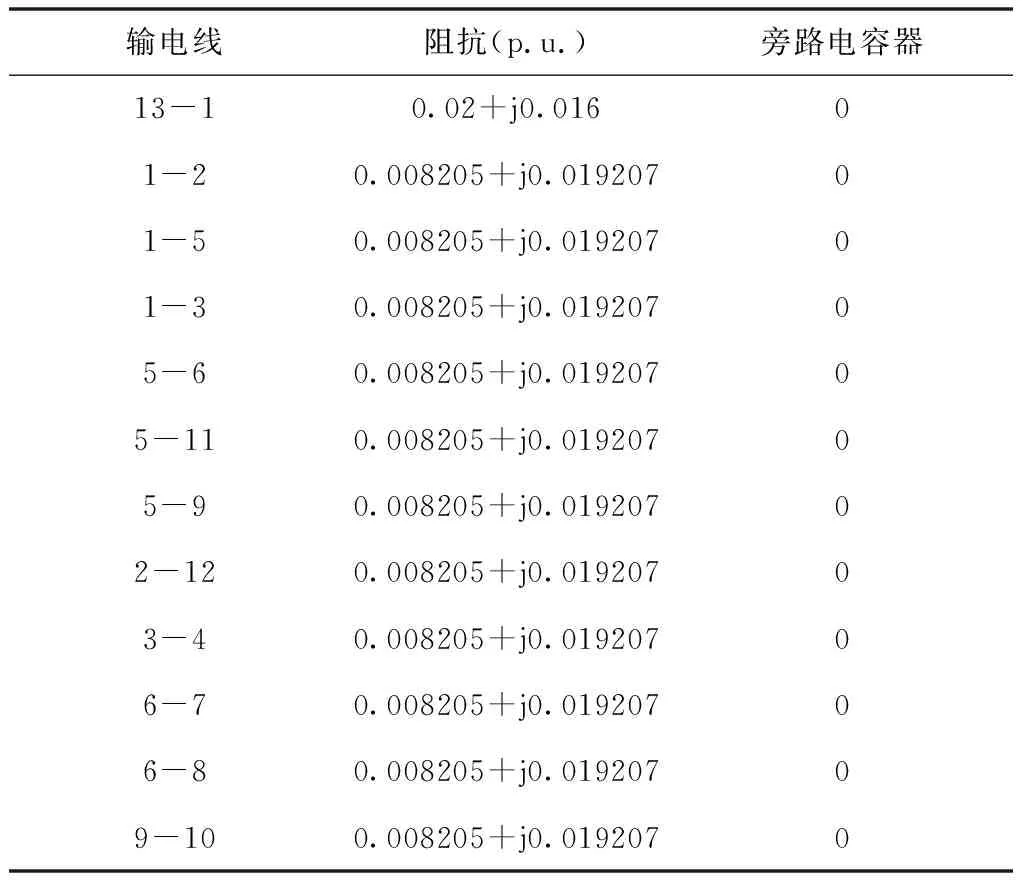
表1 电力系统主要参数

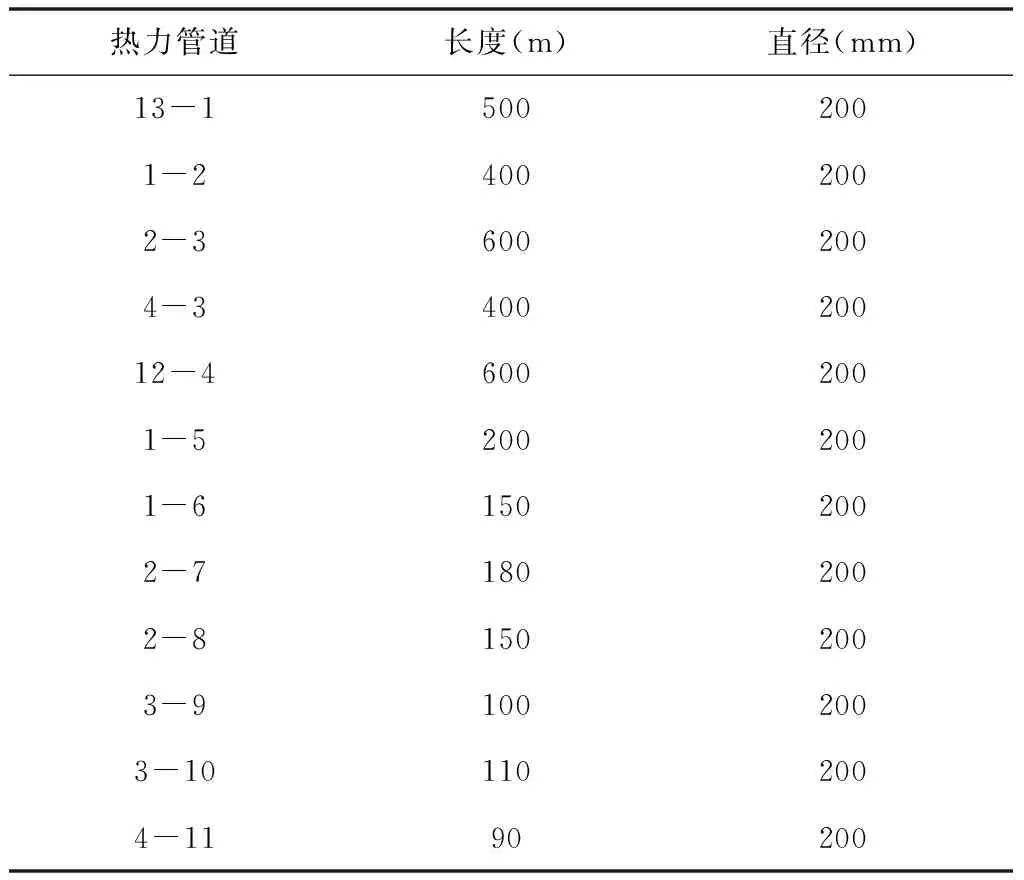
表2 热力系统主要参数

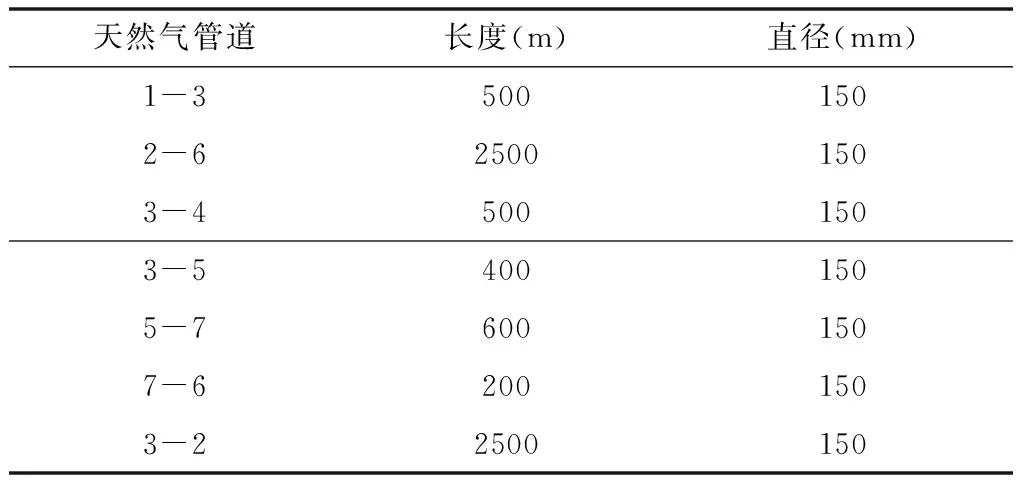
表3 天然气系统主要参数

天然气管理站调度天然气，在不同情况下保证供应给工厂的天然气量。由于GB1、GB2和GB3不存在气体负荷，因此输送到IES的气体量等于流经GB1到GB2的气体量。电网管理站负责保障有功功率流、无功功率流，以及电站与电网连接点的电压处于正常水平。为了减少IES对电力系统的影响，电网，电流和连接点的电压是固定的，因此IES的随机行为对电网没有影响。IES管理站控制12母线的电网、12支路的热网、7管带压缩机的天然气网。由于光伏发电和建筑供暖热力负荷是随机因素，因此IES管理站必须调度CHP以确保不同场景下的多重能量平衡。CHP1采用面向电网的操作模式，承担固定发电的任务，因此场景没有不确定性，而CHP 2则采用面向热量的操作模式。

综上所述，天然气系统和CHP 2是具有随机特性的调度对象，为了工业系统的安全稳定运行，应该仿真出它们的场景。仿真中使用的天然气系统和CHP运行参数如表4所示。

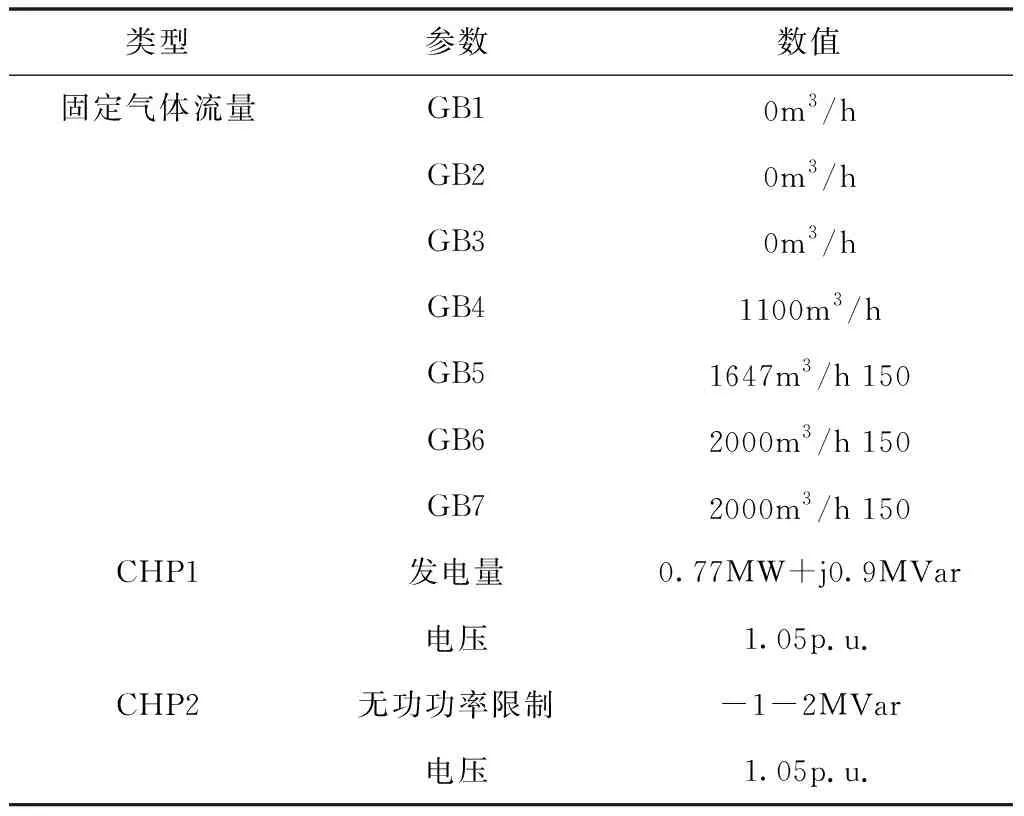
表4 天然气系统和CHP的主要参数

4.2 天气场景仿真

温度和太阳辐射强度总是随二者的联合分布和相关性的变化而变化。不同的天气相关性可以表示不同的天气情景，相关性的程度不同，天气情景的类型也不同。在以往的研究中，已经发现Copula函数可以精确地捕捉到各种天气相关性，因此利用Copula函数可以准确地仿真温度和太阳辐照度CDF的联合分布规律。本文在考虑天气因素相关性的基础上，根据1999年1月31日至1999年2月18日的小时级真实数据分别仿真了500个温度和光照强度的样本数据，其中原始光照样本服从[1.1158，2.6830]的Beta分布。仿真结果如图5和图6所示。

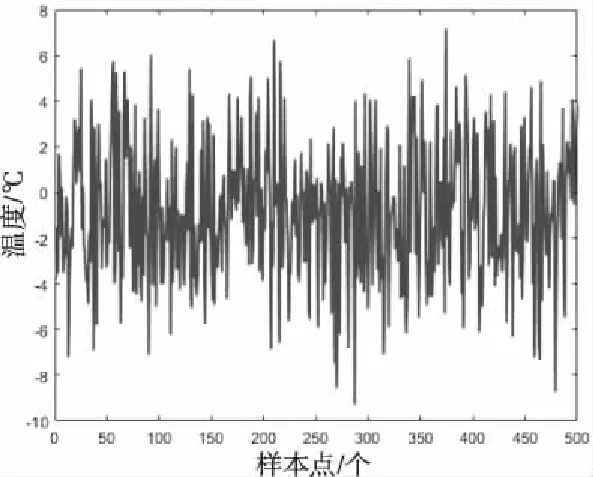
图5 500个温度样本

图6 500个光照样本

图5的温度在-10℃至8℃之间，符合仿真地区冬季的温度。图6中的光照全部大于0，是因为光伏在白天出力，光照小于0的情况没有意义的。

光伏出力和供暖热力负荷的仿真结果如图7和图8所示。其中图8的热功率是设定室内温度23℃时得出的结果。

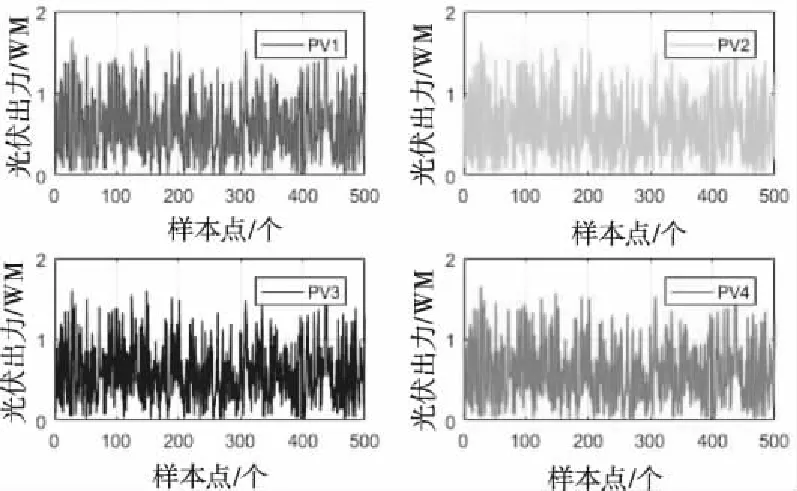
图7 光伏出力图

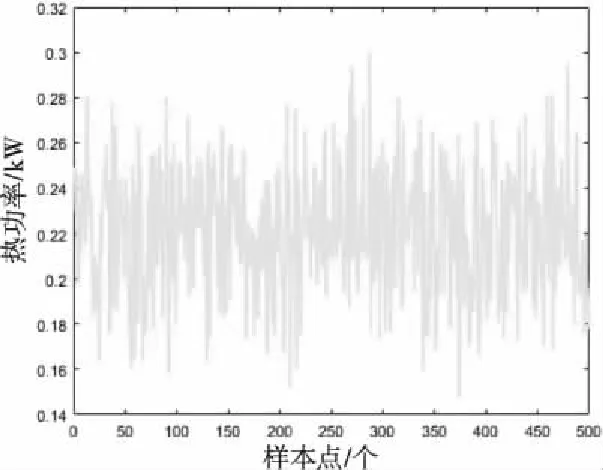
图8 热功率图

4.3 PPF快速计算

将500个样本的光伏出力和热力负荷共15个维度作为原始输入样本，4.1节中IES计算出的综合概率潮流中的光伏电压作为输出响应量，两种方法得出的光伏电压概率特征对比如图9所示。其中PCA方法中的阈值设定为0.95，经过降维后低维维数为2。

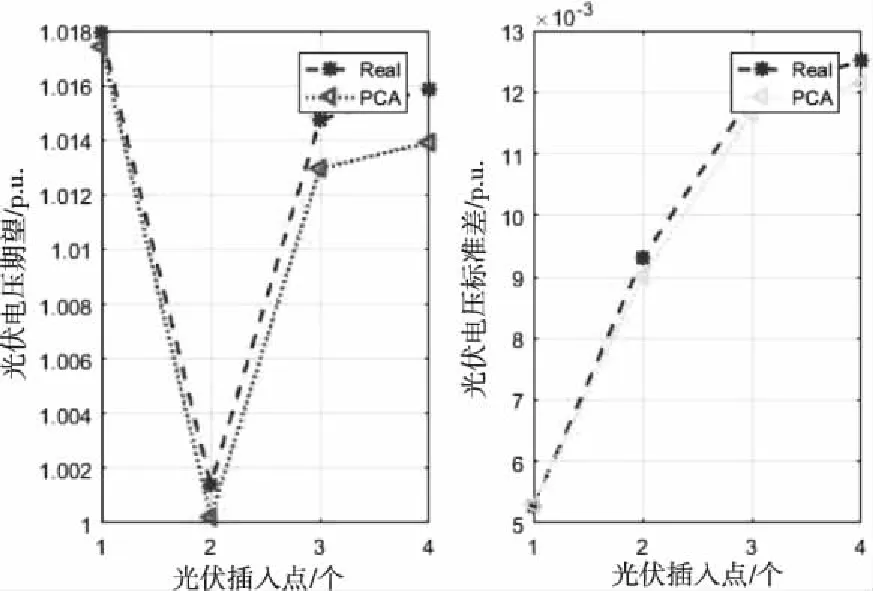
图9 4个光伏电压的概率特征

从各光伏电压的期望和方差结果来看，电压波动较小，较为稳定。从图9中可以看出，经过PCA算法降维处理后的数据与真实值之间拟合曲线的趋势大体相同，误差较小，数量级可精确到小数点后三位。PCA降维的数学机理是矩阵分解，其好处在于运算速度快，且在寻求低维结果的过程中，优化条件较少，公式推导过程严谨，这就意味着对数据集的转化操作较少，因此结果偏差较小。此外，利用基于统计机器学习的SRSM方法进行回归拟合时，所用样本数小于数值建模方法，因此也减小了计算量，提高了计算速度。

4.4 需求响应

冬季室内人体最佳舒适温度为19℃～24℃，因此本文探究了在6个温度变化下光伏并网电压、天然气消耗量和CHP负荷率的概率特征变化，根据室内设定温度的变化实现热负荷的需求响应。

图10 各温度下总天然气消耗量

图10展示了各温度下的总燃气消耗量，可以看出温度的改变也会影响总天然气消耗量的数值。图11展示了各温度下总天然气消耗量的概率特征，其期望是线性递增的，符合仿真系统的天然气消耗随热负荷的增加而增长。

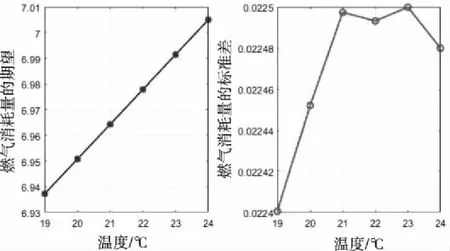
图11 各温度下总天然气消耗量的概率特征

图12和图13展示了各温度下光伏并网电压的概率特征，图12中的期望在正常状态0.95p.u.～1.05p.u.之间。图13中的光伏电压3和光伏电压4的方差相对来说较大，因此反映出数值波动较大。

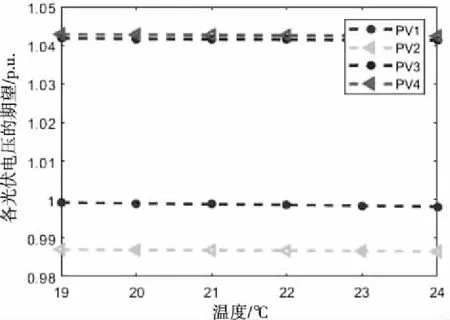
图12 各温度下光伏电压的期望

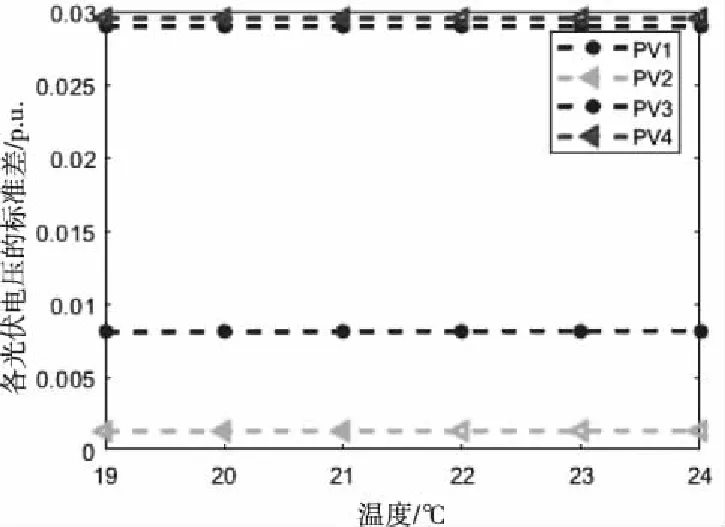
图13 各温度下光伏电压的标准差

从图14中可以看出，CHP负荷率随温度的升高而增大，增大趋势逐渐变缓。

图14 各温度下CHP的负荷率

综合以上几个参数在不同温度下的比较，可以认为在室内设定温度为19℃时能达到经济性和舒适性的平衡。

5 结论

针对含电、热、气的IES系统，本文研究并提出了一种基于统计机器学习的能源网需求响应策略，在对IES进行不确定性分析时考虑了天气相关性对结果的影响。还提出了一种名为PSRSM的PPF快速计算方法，将特征提取方法PCA与回归模型SRSM相结合并应用到综合潮流计算中。为探究室内控制温度对实现热力负荷需求响应的影响，仿真中量化了不同热力负荷需求响应策略下天然气系统、CHP运行的结果。根据仿真结果，所得结论如下：

1) 所提出的PCA降维算法与SRSM模型相结合的PSRSM综合潮流快速计算仿真方法与传统的数值模型法相比，在保证精度的前提下减小了计算复杂度，提高了运算速度，证明此仿真方法是有效的。

2) 通过仿真量化数据，综合考虑室内控制温度对光伏并网电压、总天然气消耗和CHP的影响，发现仿真制定冬季热负荷需求响应策略时，室内温度控制在19℃的效果最好。

3) 提出的需求响应仿真模型通过调节不同热网节点的热力负荷大小，可以满足居民采暖和电力系统经济运行的双重要求。