问题链教学法在高职“高等数学”教学中的应用
——以“一元函数的极值”为例
2022-10-25许素贞
许素贞
江西师范高等专科学校 江西鹰潭 335000
“高等数学”是高职院校的一门重要的公共基础课,它不仅为后续许多专业课程的学习奠定了基础,还对学生学习能力和思维能力的培养起到了十分重要的作用。该课程内容抽象、逻辑严密、应用广泛,教师若采用传统的灌输式教学方法进行知识讲授,学生难以接受。本文以“一元函数的极值”为例,坚持以学生为中心,紧紧围绕着脉络清晰的问题链展开教学,使得教学目标有效达成,学生的学习能力、思维能力、分析解决问题能力得到显著加强。
一、问题链教学法的含义
问题链是指由一系列层次分明、环环相扣、具有逻辑性和系统性的问题构成的问题链条。问题链教学法是基于学生学习基础,围绕教学目标,结合生活实际,紧扣教学重难点设计问题,以环环相扣、层层递进的“问题链”来引导教学的方法。
二、高职“高等数学”教学中存在的问题
(一)学生基础薄弱,知识晦涩难懂,难以深入理解
高职学生普遍数学基础薄弱,学习主动性不强,认为数学理论晦涩难懂,对知识缺乏深入的理解,对学习数学充满畏惧。
(二)教学方法传统,教师作为主体,能力难以提高
“黑板+粉笔”的讲授式教学法是最传统的教授数学的方法,在课堂上,教师是教学的主体,学生在听课的过程中获取新知,缺乏独立思考,难以锻炼和提高自身的学习能力。
(三)教学内容抽象,教学过程枯燥,学习缺乏兴趣
“高等数学”是一门脱离实际、高度抽象的理论性课程,学生普遍认为这样的知识点十分难学。教师在教学过程中关注知识点本身,忽略知识的来源与作用,学生为了应对考试而被动学习,学习过程枯燥,学习兴趣不佳。
三、问题链教学法在高职“高等数学”中的应用——以“一元函数的极值”一元函数的极值为例
“一元函数的极值”是一元函数导数的后续内容。它来源于实际问题,又可用于解决许多实际问题,在生活中有广泛的应用。诸如利润最大最小、距离最短、成本最小等问题,都可以转化为极值问题。下面基于问题链教学法,以“一元函数的极值”为例进行教学实践。
(一)创设情境,引发思考
教师从生活中的案例引入,展示我国的壮丽河山(黄山),在连绵起伏的群山之中,各个山峰之顶,虽然不一定是群山之中的最高处,但它却是其本身附近点的最高处。同样,各个山谷虽然不一定是群山之中的最低处,但它却是附近所点的最低处。由此提出问题:山峰和山谷在数学上如何刻画呢?这就是我们要学习的极值,引出主题。
(二)尝试探索,建立新知
1.模块一:一元函数极值的定义
教师用函数曲线来模拟黄山,引导学生探索极值的定义,设计问题链:
问题1:什么是函数的极大值?(学生根据图片引导及自身理解进行回答。)
问题2:如何用不等式刻画函数极大值的含义?(f
(x
)>f
(x
))问题3:什么是函数的极大值点?(强调极大值点并非一个点的坐标。)
问题4:什么是函数的极值?什么是函数的极值点?
函数极值的概念:已知函数y
=f
(x
),设x
是定义域(a
,b
)内任一点,如果对x
附近的所有x
(x
≠x
),都有f
(x
)>f
(x
)(f
(x
)<f
(x
)),则称函数f
(x
)在点x
处取极大(小)值,x
称为函数f
(x
)的一个极大(小)值点。函数的极大值与极小值统称为极值,极大值点与极小值点统称为极值点。教师引导学生在实际生活中抽象出数学概念,既帮助学生理解极值的概念,也让学生感受到数学来源于生活。
2.模块二:一元函数极值的求法
教师引导学生看图回答以下问题:
问题5:图1中函数在哪些点处取得极值?(x
、x
、x
、x
)问题6:图1中函数在极值点x
、x
、x
处的切线,有什么特征?(切线水平,斜率为零,函数f
(x
)在这些点处导数为零。)问题7:导数为零的点一定是函数的极值点吗?(不一定,比如图1中函数f
(x
)在点x
处导数为零,但x
却不是函数的极值点。注:导数为零的点称为驻点。)问题8:极值点除了导数为零的点,还有其他的点吗?(有的,还有可能是不可导的点,比如图1中x
是函数f
(x
)的极值点,但函数f
(x
)在该点处导数不为零,x
是函数f
(x
)的不可导点。)问题9:观察图2,满足什么条件的点是极值点呢?(口头总结判定极值的充分条件。例如:在点x
的左侧,函数是单调递增的;在点x
的右侧,函数是单调递减的。左增右减正好形成了一个高峰,这个点正好是极大值点。)问题10:如何判断函数的单调性?(导数大于零,函数单调递增;导数小于零,函数单调递减。)
问题11:如何求解函数的极值?(学生探索出求解函数极值的第一种方法,并梳理出具体步骤。)
求解函数极值(方法一)的步骤:
(1)求函数f
(x
)的定义域;(2)求导数f
′(x
),找出f
(x
)的所有驻点(导数为零的点)及导数不存在的点;(3)用以上点将定义域分成若干区间,求各区间导数符号,判别函数的单调;
(4)求出极值。
组织学生利用Geogebra画板画出函数f
(x
)=x
+2x
、函数f
(x
)的一阶导函数f
′(x
)=3x
+4x
及函数f
(x
)的二阶导函数f
″(x
)=6x
+4的图像。具体图像如图3所示,图3中S形曲线代表函数f
(x
)的图像,抛物线代表函数f
(x
)的一阶导函数的图像,实直线代表函数f
(x
)的二阶导函数的图像,两条虚线分别经过函数f
(x
)的极大值点和极小值点。问题12:观察图3,函数f
(x
)极大值点左右两侧的一阶导数有什么特征?(左侧一阶导大于零,右侧一阶导小于零,与方法一的判定原理一致。)问题13:观察图3,函数f
(x
)在极大值点处的二阶导数有什么特征?(在极大值点处的二阶导数小于零。)问题14:观察图3,函数f
(x
)极小值点左右两侧的一阶导数有什么特征?(左侧一阶导小于零,右侧一阶导大于零,与方法一的判定原理一致。)问题15:观察图3,函数f
(x
)在极小值点处的二阶导数有什么特征?(在极小值点处的二阶导数大于零。)问题16:还可以找到求解函数极值的其他方法吗?(学生探索出求解函数极值的第二种方法,并梳理出具体步骤。)
求解函数极值(方法二)的步骤:
(1)求函数f
(x
)的定义域;(2)求一阶导数f
′(x
)、二阶导数f
″(x
),找出f
(x
)的所有驻点;(3)判断在驻点处函数f
(x
)的二阶导数的符号(大于零还是小于零);(4)求出极值。
注1:方法二只能用来判断驻点是否为极值点,不可导点是否为函数极值点仍需用方法一来判断。

图1

图2
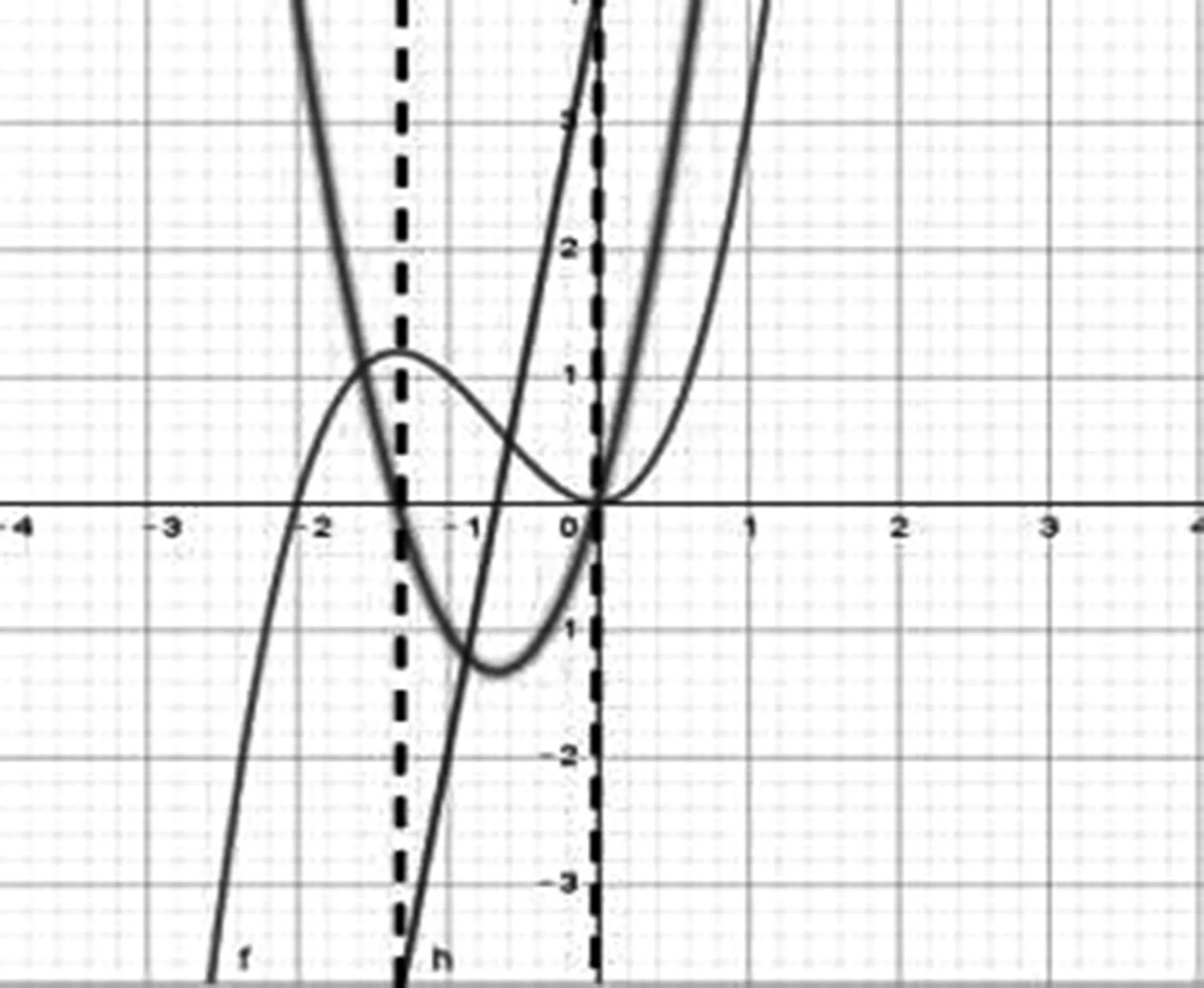
图3
在教学过程中,为引导学生探索极值的求法,从学生已有的知识经验(学生已经理解导数的定义、计算、几何意义,并且掌握了利用导数判定函数单调性的方法)出发,借助问题链的实施,在已知与未知之间搭建桥梁。学生在教师的引导下,主动回顾旧知,深入探究问题,理清知识脉络,最终获得求解函数极值的两种方法。
3.模块三:例题演练
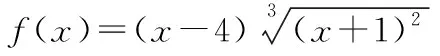
f
(x
)的定义域:f
(x
)在(-∞,+∞)内有定义且连续;(2)求导数f
′(x
),找出f
(x
)的所有驻点及导数不存在的点:
(3)判断单调性:
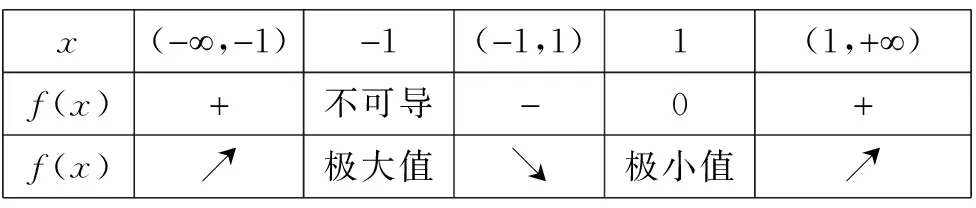

f
(x
)=(x
-1)+1的极值。解:(1)求函数f
(x
)的定义域:f
(x
)在(-∞,+∞)内有定义且连续;(2)求一阶导数f
′(x
)、二阶导数f
″(x
),找出f
(x
)的所有驻点:f
′(x
)=6x
(x
-1),f
(x
)=6(x
-1)(5x
-1);令f
′(x
)=0,求得驻点x
=-1,x
=0,x
=1;(3)判断在驻点处函数f
(x
)的二阶导数的符号:f
″(0)=6>0,f
″(-1)=f
″(1)=0;(4)求出极值:f
(x
)在x
=0处取得极小值,极小值为f
(0)=0;因f
″(-1)=f
″(1)=0,用方法二无法判别,需选用方法一;在-1的左右邻域内f
(x
)皆小于零,所以f
(x
)在x
=-1处没有极值;同理,f
(x
)在x
=1处也没有极值。注2:二阶导为零的驻点是否为函数的极值点仍需用方法一来判断。
(三)课堂总结,拓展应用
教师借助问题链中的主干问题“什么是函数的极值?如何求解函数的极值?”引导学生对一元函数极值的教学内容进行梳理,并设置实际问题,拓展应用。
拓展应用:某一公司生产某种产品Q件,总成本为C(Q)=5Q+200,得到的总收益为R(Q)=10Q-0.
01Q,求生产该产品多少件可以获得最大的利润?四、在高职“高等数学”教学中应用问题链教学法应注意的问题
(一)问题链的设计要符合学生基础,关注学生困惑,能辅助学生进行知识探索
设计问题链时,问题太难,会使学生缺乏思考空间,问题过于简单,会使得问题本身失去思考的价值,所以,创设难易度适合的问题尤为重要。问题的设置要充分考虑学生的学习基础,同时又要关注学生容易产生困惑的点,设置的问题应具备思考性和探索性,能辅助学生在循序渐进的基础上获取新知。
(二)问题链的设计要逻辑严密,层层递进,能启迪学生思维、培养学生能力
设计问题链时,设置的问题应具有逻辑性,缺乏逻辑性的问题会打乱学生的思维,不利于学生逻辑思维能力的培养。设置的问题应具有层次性,上一个问题的解决为下一个问题做好铺垫,通过层层设疑,引导学生慢慢地接近最终答案。学生作为解决问题的主体,在逻辑严密、层层递进的问题链的引导下独立思考,积极探索,自觉地掌握知识内容和提高分析问题、解决问题的能力。
(三)问题链的设计要贴合实际,环环相扣,能提升学习兴趣,凝聚学生注意力
脱离实际、高度抽象的“高等数学”让学生为之却步,为了克服数学课理论性强、趣味性不够的问题,在设计问题链时要尽量做到贴合实际,环环相扣。获取的知识点从实际生活而来,用到实际生活中去,不仅可以加深学生对知识内容的理解,同时可以大大提升学生的学习兴趣,凝聚学生注意力。
(四)问题链的设计要围绕教学目标,紧扣教学重难点,能达成良好的教学效果
问题链教学课堂要避免盲目设问,问题的设置应紧紧围绕课程的教学目标,教学目标是教学设计和实施的依据。基于教材内容,围绕教学目标,紧扣教学重难点,前后问题的内容设置应具有连贯性,共同指向核心问题。一个接一个问题的顺利解决,直到核心问题的解答,达成教学目标,这样的学习才是有意义的学习。
教学中灵活运用问题链教学法,能够对高职数学教学的改革与创新起到积极的推动作用。在今后的“高等数学”教学中,将问题链教学法合理运用,将知识点转化为层层递进的问题链,用问题来组织教学,引导学生通过自主探索的方式来建构对知识点的理解,让学生真正成为学习的主体,能够提高学生独立思考的思维能力和实际解决问题的操作能力,能够真正学有所获,起到助力终生持续性学习的作用。
