基于ABAQUS的加筋球壳参数化建模及屈曲分析

彭宇辰，陈秀华，吴亚东

（1.上海交通大学 机械与动力工程学院，上海 200240）（2.上海交通大学 航空航天学院，上海 200240）

0 引言

加筋球壳结构由于其抗屈曲性能良好，并且具有较高的结构效率和可设计性，广泛应用在航空航天领域中各类承力构件。典型的加筋球壳结构如飞机后压力框，其加筋设计和布置有很多方式。例如空客A340的后压力框采用了只加经向筋的方式进行设计，而波音747则采用了经纬向格栅加筋的方式进行设计。加筋球壳结构在承受外压载荷时需要考虑屈曲问题，同时当前航空航天领域对于减重的需求愈发迫切。因此，如何通过对加筋球壳结构的筋条布置及各项参数进行设计用以实现在减重的同时获得较高的屈曲载荷变得十分重要。

对于球壳结构的稳定性问题，研究者已对此展开了研究。J.Btachut针对扁球壳结构的屈曲问题进行了实验和有限元分析；Wang Jingchao等基于能量法，给出了加筋正交各向异性扁球壳非线性屈曲的广义相似条件和缩尺原理；庞福振等针对加筋球壳结构的稳定性进行分析，讨论了球壳厚度、加强形式对加筋球壳结构稳定性的影响并进行了一定的优化；马玉斐等对经线加筋和纬线加筋这两种加筋形式的加筋球壳进行了局部和总体稳定性计算；蔡奕霖等采用有限元法分析均布外压作用下复合材料扁球壳结构的屈曲和后屈曲行为，讨论了铺层顺序等对屈曲及后屈曲行为的影响并进行优化设计；罗珊等基于弧长法对受压球壳的稳定性进行了分析，并对含初始缺陷受压球壳的稳定性进行研究；张猛等针对不锈钢球壳进行静水压力试验与数值仿真分析；李富根等利用渐近迭代法获得了边界弹性支撑的S型功能梯度扁球壳的非线性屈曲问题的理论解。但在目前研究中，球壳结构的加筋设计形式相对较少，所建立的有限元模型也只选取了几种相对简单的方式，尚未给出任意尺寸及加筋布置方式下加筋球壳结构的参数化有限元模型，同时也未给出加筋结构对临界屈曲压力与重量之比的影响规律。

为了提高有限元建模效率，研究者采用参数化模型来对某一飞机部件进行设计。郭英男等开发了航空连接结构参数化有限元分析系统；蒋华兵等通过对ABAQUS二次开发，建立了数控弯管专用前处理模块；年春波等基于ABAQUS二次开发，对变角度层合板的屈曲特性进行了分析；Jin Bocheng等利 用PCL语 言 对Patran进 行二次开发，通过建立参数化模型对单板和多板的帽型筋加筋板进行了分析，研究相关几何参数的设计敏感性；Tang Jiapeng等提出了飞机机翼结构的有限元参数化建模方法。但目前尚未有文献报道给出双曲加筋球壳结构的参数化有限元建模方法。

本文给出基于ABAQUS的加筋球壳结构的参数化有限元建模方法，并利用其对铝合金加筋球壳的屈曲问题进行参数化分析；根据有限元分析的结果，归纳各主要设计参数对整体结构屈曲的影响规律，以期为加筋球壳结构的减重优化设计提供参考。

1 加筋球壳结构有限元模型的参数化建模

1.1 有限元建模方法

参数化建模的实现过程与有限元模型的建模过程相类似。由于球壳与加强筋分布一般采用周期性对称结构，因此可以通过建立扇形模型利用周期性实现整个加筋球壳参数化模型的建立，其中球壳曲面采用壳单元，加强筋则采用一维梁单元。加筋球壳结构示意图如图1所示。

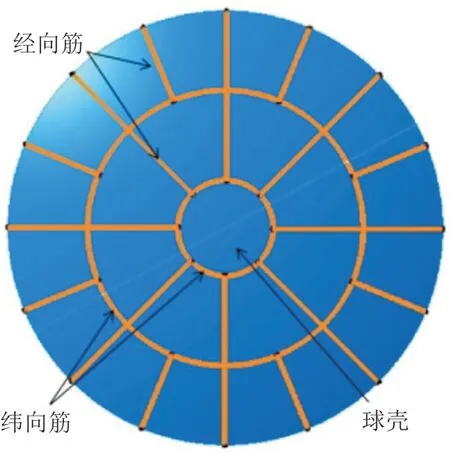
图1 加筋球壳结构示意图Fig.1 Diagram of stiffened spherical shell structure

1.1.1 扇形球壳几何模型建模

扇形曲面模型示意图如图2所示，对于扇形球壳曲面部分，主要参数包括底面半径a，拱高h，壳厚t以及扇形周期数n，扇形模型的圆心角α的大小根据扇形的周期数n得到。上述参数构成了整个球壳结构的基本几何尺寸。

图2 扇形曲面模型示意图Fig.2 Schematic diagram of fan-shaped surface model

通过改变上述参数大小即可实现扇形球壳曲面的快速建模。根据底面半径a及拱高h即可计算出曲率半径R的大小。

1.1.2 扇形几何模型的拆分及网格划分

对于整个模型的几何拆分和网格划分，主要的难点在于不仅需要确定加强筋所在的位置，同时还需要保证球壳所划分的网格与加强筋网格相对应。根据纬向筋和经向筋的位置和数量对曲面进行合适的拆分，通过对拆分所形成的几何边进行布种数量控制完成球壳曲面网格划分。

对于扇形几何模型的拆分，如图3所示，主要是根据经向筋和纬向筋的位置和数量来确定的。首先根据纬向筋的位置将整个扇形模型分成i个区域，i为纬向筋数量。对于距球壳中心的距离为0～r的区域，默认没有加强筋，对于r～r的区域在右侧默认有一条经向筋。若整个模型需要额外加经向筋，则将该区域按照最少的经向筋个数均匀拆分，若整个模型不需要额外加经向筋，则不再对该区域进行拆分。对于距球壳中心的距离为r～r的区域，根据最大经向筋个数n均分该区域。这样拆分的目的是为了之后划分的网格更加规则。

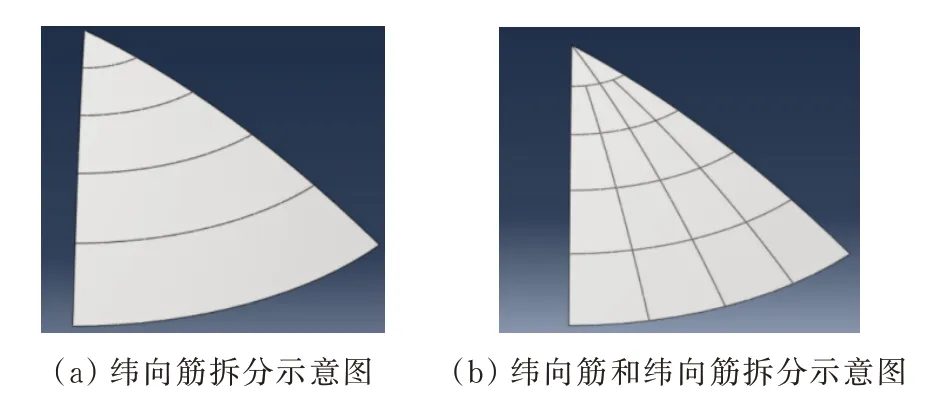
图3 扇形几何模型拆分示意图Fig.3 Schematic diagram of division of fan-shaped model

对扇形模型进行几何拆分后，对其进行网格划分。网格划分主要的控制参数为径向和环向的布种个数。对于径向的几何边通过设置相邻种子之间的间距s来控制布种个数，而环向的几何边则通过调节一定的比例系数m来实现布种个数的控制，球壳曲面的单元类型为S8R。不同密度的网格划分示意图如图4所示。

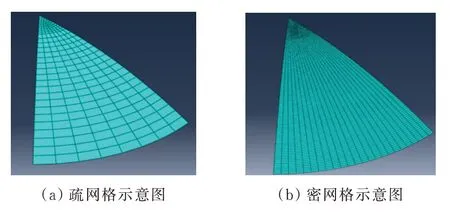
图4 不同网格密度划分示意图Fig.4 Division of different mesh density

1.1.3 加强筋建模

对于加强筋部分，为了便于参数化建模进行一定简化，采用球壳外部加筋方式，通过一维梁单元来进行表示，单元类型为B31。在该模型中，加强筋采用与球壳网格共节点的方式进行建模，即认为加强筋与球壳之间是完美连接的，不考虑球壳与加强筋脱开的情况。通过对球壳划分网格后，将所需位置的节点按x坐标的大小排序后依照从小到大的顺序两两相连来建立梁单元。

对于纬向筋建模，主要的控制参数为纬向筋的数量i以及纬向筋的位置r～r。r～r由纬向筋距球壳中心距离与球壳底面半径之比C进行控制，如图5所示。通过表格来对纬向筋的位置和个数进行控制，只需改变相应参数即可实现不同纬向筋位置的快速建模。在该模型中，默认最大半径处有纬向筋，因此C≡1。

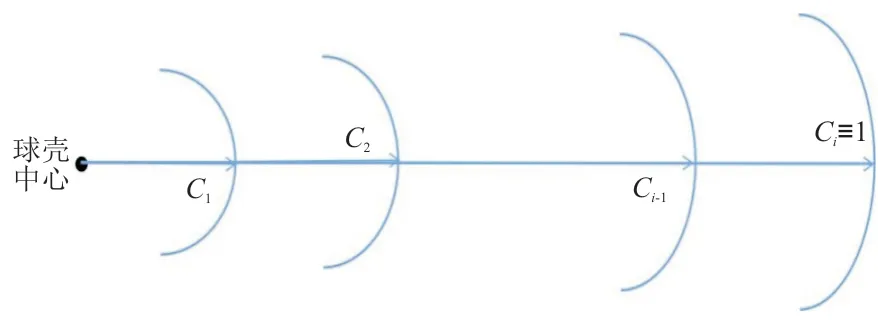
图5 纬向筋位置控制参数示意图Fig.5 Schematic diagram of position control parameters of circumferential stiffeners

对于经向筋的建模，相邻两个纬向筋之间区域中经向筋的数目均匀布置。主要的控制参数为相邻两个纬向筋之间区域中经向筋的数目N～N。对于距球壳中心的距离为0～r的区域，默认没有加强筋，对于r～r的区域在右侧默认有一条经向筋，最内层没有经向筋。通过表格对一个扇形模型上的经向筋个数来进行控制，使得相邻两个区域上的经向筋的个数相互关联。I为第一个纬向筋与第二个纬向筋之间增加经向筋个数，即N=I+1。N～N则通过F（j=1，2，…，i-2）进行控制：当F为0时，表示下一层不需要额外加筋，即下一层增加的经向筋个数与上一层相同，N=N；当F=1时，表示下一层需要额外加筋，下一层的经向筋个数变为上一层的2倍，即N=2N。生成的加筋扇形模型如图6所示，图中绿色部分即为加强筋。

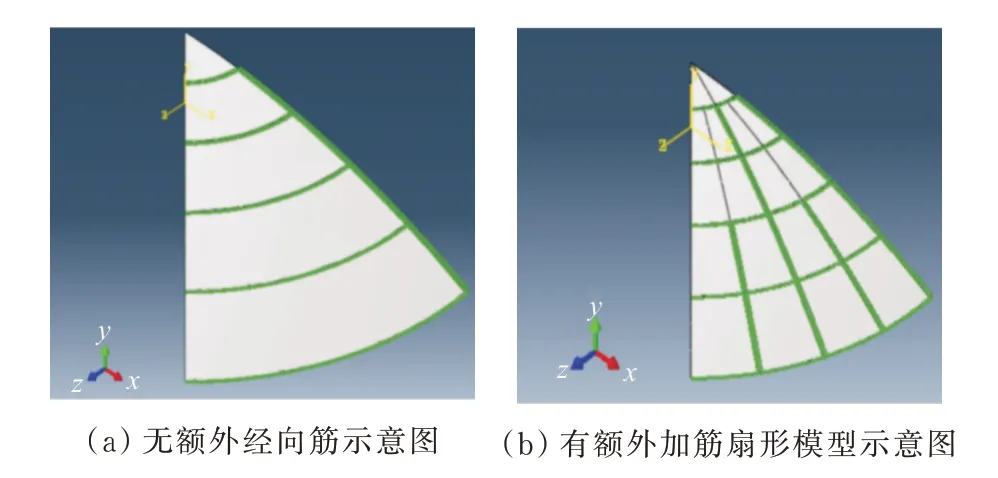
图6 纬向筋数目为5，无额外经向筋和有额外加筋扇形模型示意图Fig.6 Diagram of fan-shaped model with 5 circum ferential stiffeners，without extra meridional stiffeners and with extra meridional stiffeners

在目前所使用的模型中，梁单元截面采用矩形截面，根据实际模型需要可以更换为梯形、T型或I型截面等不同梁截面形状。对于矩形截面，主要的设计参数为梁截面的宽度b和厚度t，通过改变这两个参数即可实现任意矩形梁截面的建模。

由于本模型采用球壳外部加筋方式，为保证加强筋与球壳曲面的相对位置关系与实际相符，需要对梁截面进行偏心操作，如图7所示，对梁单元的方向进行设置，保证梁截面的1方向为宽度方向，梁截面的2方向为厚度方向。在全局坐标系下，对于纬向筋，当梁单元z坐标大于0时，梁单元的1方向为（0，0，-1）；当梁单元z坐标小于0时，梁单元的1方向为（0，0，1）。对于经向筋，其1方向在全局坐标系下为（sinφ，0，-cosφ），其中φ为

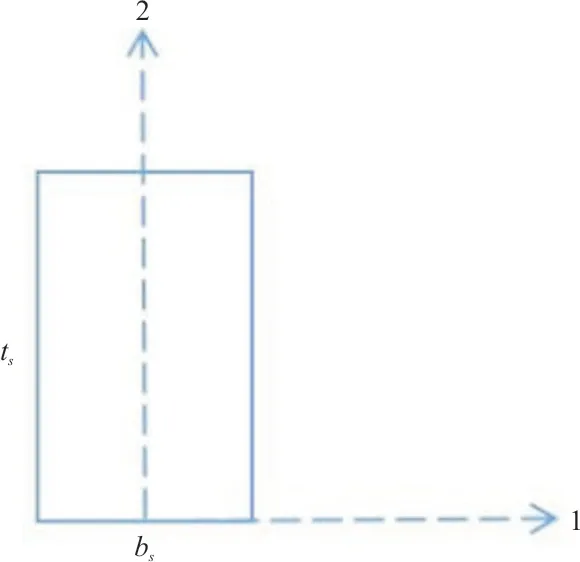
图7 加强筋梁截面示意图Fig.7 Schematic diagram of beam section of the stiffener

该经向筋与xy平面所成的夹角。

完成上述扇形几何模型建立后，根据扇形模型周期个数n，利用旋转阵列即可建立完整的加筋球壳结构几何模型。

1.1.4 载荷及边界条件

整个模型的载荷及边界条件，如图8所示，整个模型受到均布外压载荷作用，边界条件为底边固支，进行屈曲分析。根据不同的受载情况，可以对载荷和边界条件进行调整。

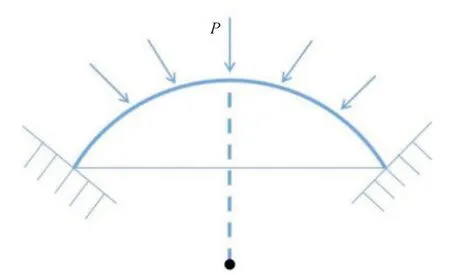
图8 载荷及边界条件示意图Fig.8 Schematic diagram of load and boundary conditions

1.1.5 参数化有限元模型

本文通过对ABAQUS二次开发来建立加筋球壳有限元参数化模型，采用python作为接口语言。依据上述参数化建模方法，创建GUI插件，实现加筋球壳结构有限元模型的快速建立。

采用该参数化有限元建模方法，只需根据需要输入相应参数，即可快速建立不同尺寸和厚度、不同材料、不同加筋形式及梁截面的加筋球壳有限元模型。所建加筋球壳有限元几何模型及网格划分示意图如图9所示。

图9 加筋球壳几何模型及网格示意图Fig.9 Schematic diagram of geometric model and mesh of stiffened spherical shell

在目前的模型中，加筋方式可以从不加筋，仅加经向筋，仅加纬向筋，格栅加筋这四种情况中进行选择。同时，加筋球壳材料属性赋予，分析步创建，载荷及边界条件施加也已完成，只需提交作业即可得到分析结果。在给定加筋球壳结构参数的情况下，采用传统有限元建模方式需要至少1 h进行有限元模型的创建，而采用该参数化有限元模型仅需要至多半分钟的时间便可完成模型的建立。

1.2 加筋球壳结构参数化有限元模型的验证

由于缺少实验数据，对于无加筋球壳，选取文献［2］的数据对模型进行验证，载荷为均布外压载荷，边界条件为底边固支；对于加筋球壳结构，选取文献［3］的模型参数进行验证，分别对底边固支和简支两种边界条件进行计算，载荷为均布外压载荷。所用模型基本参数如表1～表2所示。

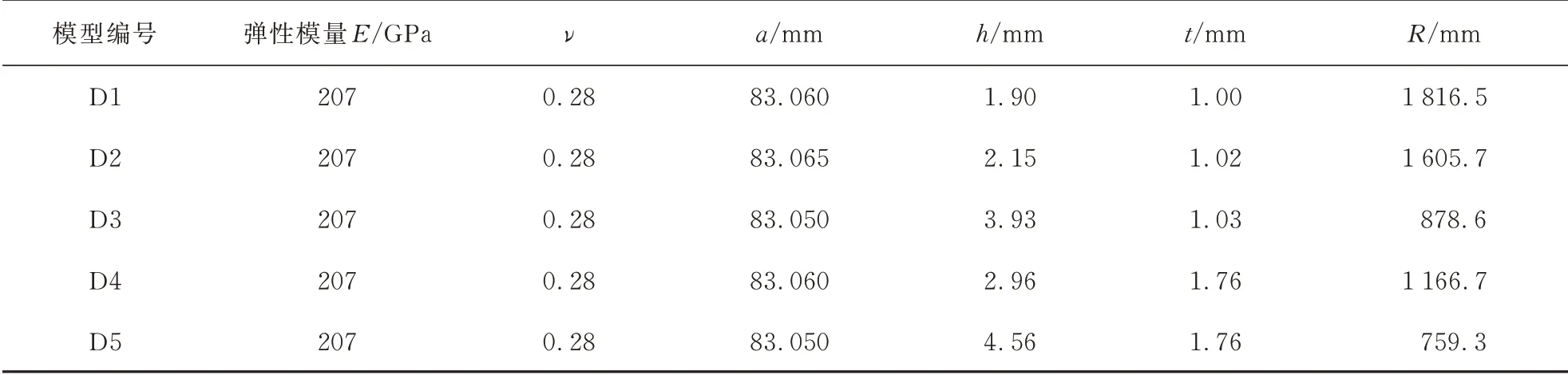
表1 无加筋球壳材料属性和结构尺寸Table 1 The material properties and dimensions of the spherical shells without stiffeners

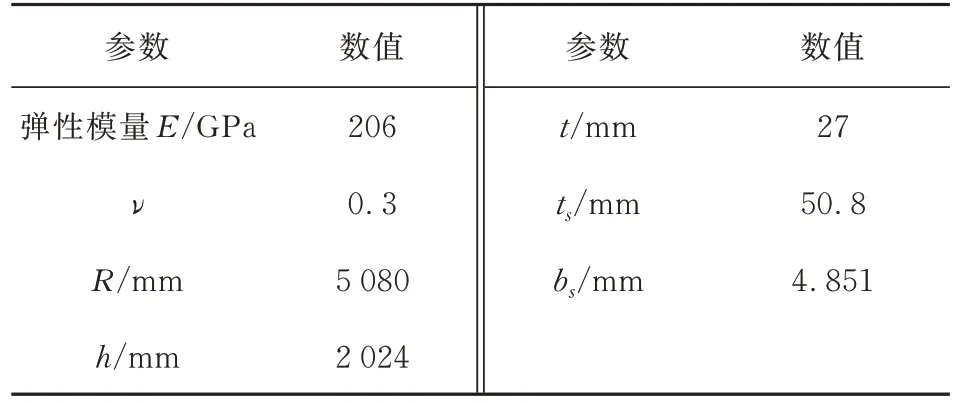
表2 加筋球壳材料属性和结构尺寸Table 2 The material properties and dimensions of the stiffened spherical shells

利用上述参数化有限元模型对所选模型进行有限元分析，并与文献［2-3］结果进行对比，结果如表3所示，其中P为文中所给出的临界屈曲压力，P为参数化有限元模型所计算出的临界屈曲压力，可以看出：该参数化模型在无加强筋与格栅加筋情况下通过有限元得到的结果均与文献结果吻合较好，因此认为通过该参数化有限元建模方法所建立的有限元模型的计算结果是可信的。

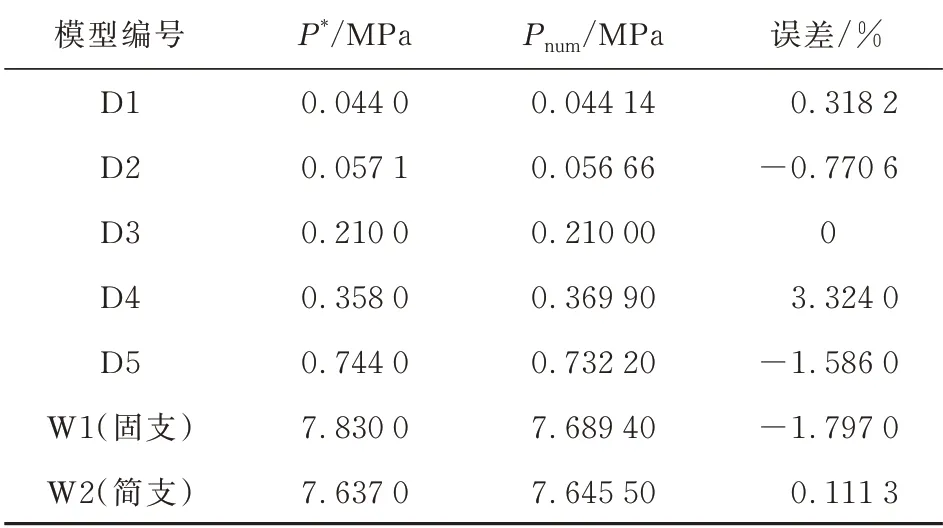
表3 文献结果与有限元结果的比较Table 3 Comparison of literature results and finite element results

2 加筋球壳结构主要参数对其屈曲性能的影响研究

随着航空航天领域对于减重的要求越来越迫切，在保证临界屈曲载荷足够的同时如何减重变得愈发重要。本文针对铝合金加筋球壳，以临界屈曲载荷P与临界屈曲载荷与重量之比P/W为主要指标，对其屈曲问题展开研究。载荷为均布外压载荷，边界条件为底边固支，通过Riks分析步进行非线性分析，模型的基本尺寸采用文献［2］中的模型D3进行计算。临界屈曲载荷P为载荷位移曲线中的极大值点，加筋球壳质量为W，铝合金球壳材料与尺寸参数如表4所示。

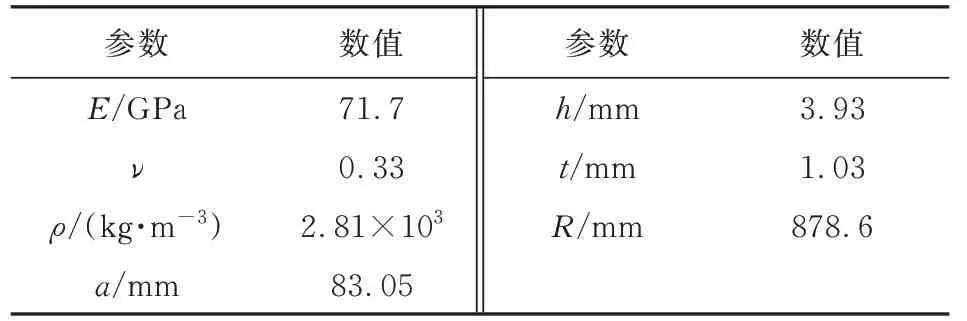
表4 铝合金球壳材料属性和结构尺寸Table 4 Material properties and dimensions of the aluminum alloy spherical shells

2.1 球壳厚度对Pc及Pc/W的影响

针对无加强筋的情况，对球壳厚度对P及P/W的影响进行研究。球壳厚度选择从1～2 mm，每次增加0.25 mm，结果如图10～图12所示。

图10 球壳厚度与临界屈曲载荷Pc关系Fig.10 Relationship between critical buckling load Pc and the thickness of shell

图11 球壳厚度与Pc/W之间的关系Fig.11 Relationship between Pc/W and the thickness of shell

图12 不同壳厚下无加筋球壳中心处载荷位移曲线Fig.12 Load-displacement curve at the apex of unstiffened spherical shell with different shell thickness

从图10～图12可以看出：随着球壳厚度的增加，临界屈曲载荷P逐渐增大，临界屈曲载荷与重量之比P/W也逐渐增大，因此增加球壳厚度可以有效地提高结构整体的屈曲性能。

2.2 加强筋主要设计参数对Pc及Pc/W的影响

球壳曲面尺寸与材料同上节一致，厚度为1 mm，加强筋截面采用矩形截面，材料与球壳一致，开展加强筋主要设计参数对P及P/W的影响研究。由于边界条件为固支，在最大半径处的纬向筋并未起到加强作用，因此在计算加筋球壳重量和纬向筋数量时减去了该部分的重量。

2.2.1 加强筋布局对P及P/W的影响

对不同加强筋布局的铝合金加筋球壳进行非线性有限元分析，加强筋截面尺寸为5 mm×1 mm（宽度×厚度），结果如图13～图15所示。

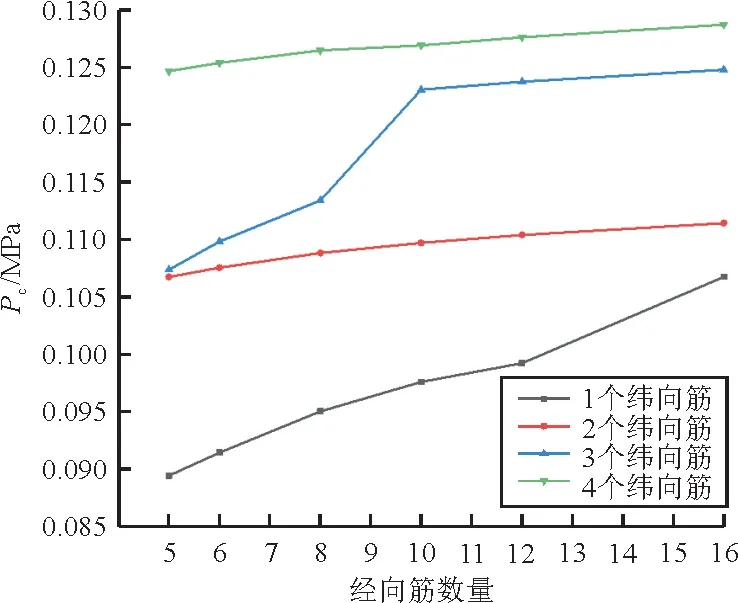
图13 加强筋布局与临界屈曲载荷Pc关系Fig.13 Relationship between stiffeners layouts and critical buckling load Pc

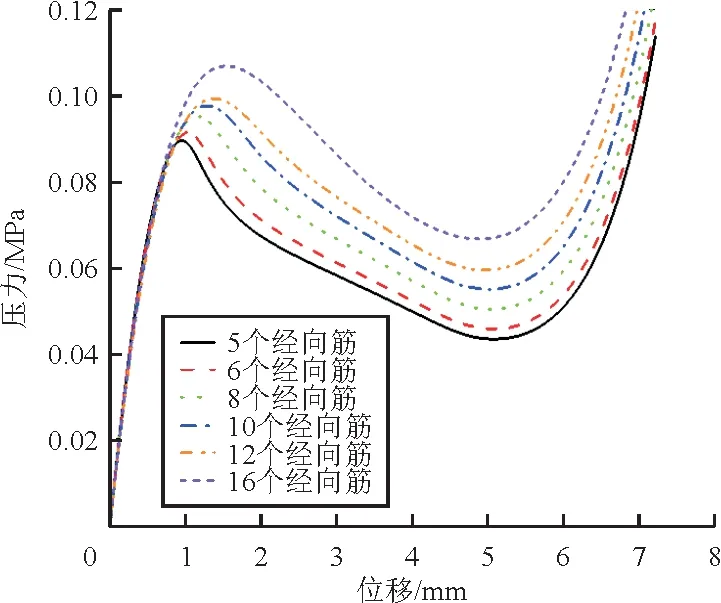
图15 纬向筋为1时不同经向筋数量下球壳中心处载荷位移曲线Fig.15 Load-displacement curve at the apex of different meridional stiffeners with one circumferential stiffener

从图13～图14可以看出：随着纬向筋数量的增加，P和P/W均逐渐增大，而随着经向筋数量的增加，P逐渐增大，而当纬向筋数目为1和3时，随着纬向筋数量的增加，P/W先增大后减小；当纬向筋数目为2和4时，随着纬向筋数量的增加，P/W则逐渐减小；当纬向筋数目为4，经向筋数目为5时，P/W取得最大值。

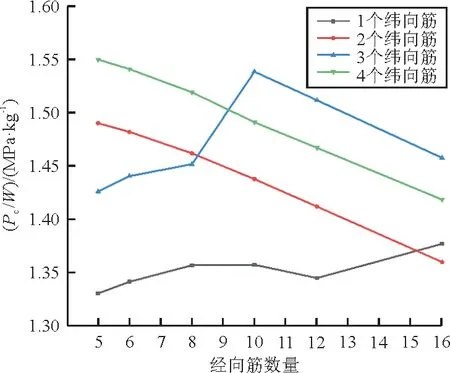
图14 加强筋布局与Pc/W之间的关系Fig.14 Relationship between stiffeners layouts and Pc/W

纬向筋位置分布如表5所示（省略了最大半径处加强筋），其中C为纬向筋距球壳中心距离与球壳底面半径之比。

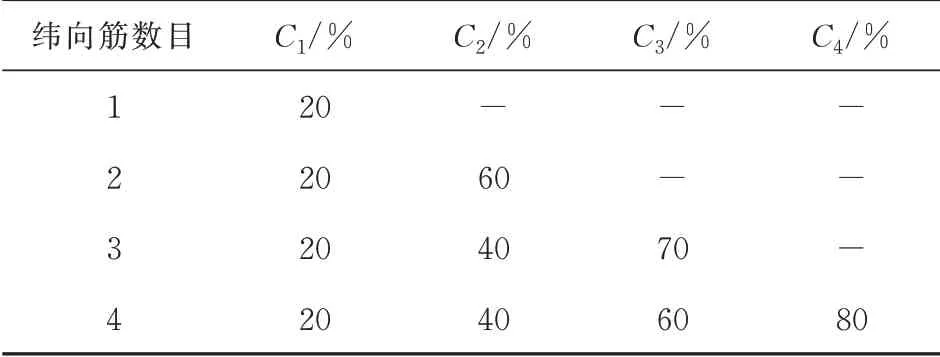
表5 纬向筋位置分布表Table 5 Location distribution of circumferential stiffeners

2.2.2 纬向筋位置对P及P/W的影响

研究纬向筋位置对P及P/W的影响，选取纬向筋数目为1时的情况，经向筋数目为8和16，加强筋截面尺寸为5 mm×1 mm（宽度×厚度），纬向筋位置距球壳中心距离与球壳底面半径之比为10%～50%，每次增加10%，进行有限元分析，得到结果如图16～图17所示。

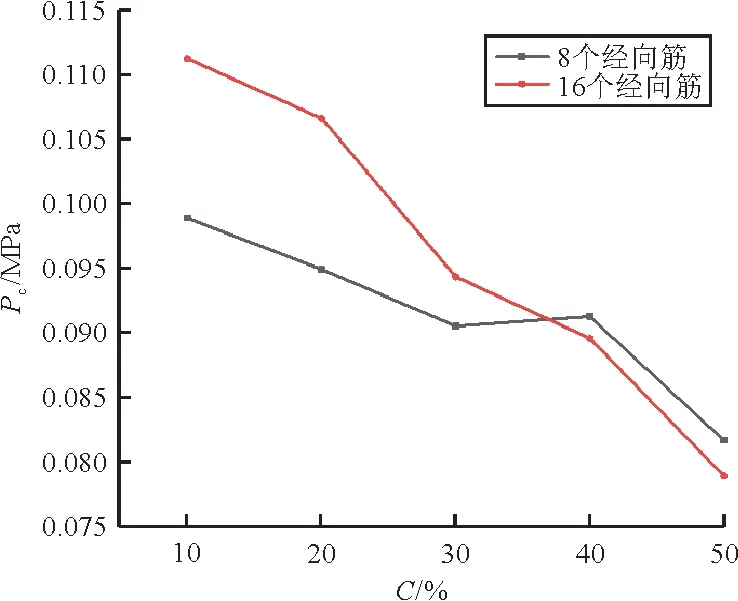
图16 纬向筋位置与临界屈曲载荷Pc关系Fig.16 Relationship between the position of circumferential stiffeners and critical buckling load Pc

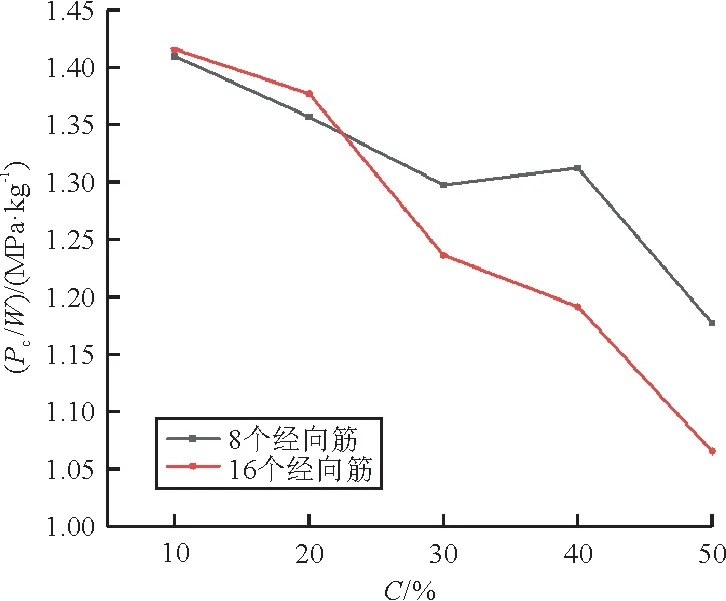
图17 纬向筋位置与Pc/W关系Fig.17 Relationship between the position of circumferential stiffeners and Pc/W

从图16～图17可以看出：当纬向筋位置距球壳中心距离越远，P和P/W均逐渐减小。因此纬向筋的位置对结构整体屈曲有很大影响，需要对纬向筋位置进行合理布置。

2.2.3 加强筋截面尺寸对P及P/W的影响

在加强筋梁截面面积一定的情况下，对不同梁截面尺寸对屈曲特征值的影响展开研究。选取球壳厚度为1 mm，纬向筋数目为1，纬向筋位置距球壳中心距离与球壳底面半径之比为20%，经向筋 数 目 为8和16，截 面 面 积 为5 mm，得 到P及P/W结果如表6～表7所示，可以看出：在梁截面面积一定的情况下，梁截面高度越高，P和P/W越大，加强筋的作用越明显，但高度也应在合理范围内进行设计。

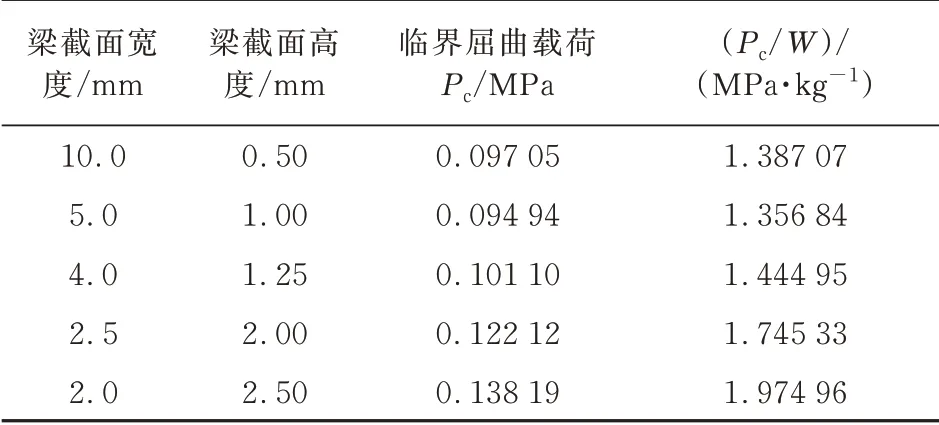
表6 经向筋数目为8时不同加强筋截面尺寸下的Pc与Pc/WTable 6 Pc and Pc/W under different stiffener section size with 8 meridional stiffeners

表7 经向筋数目为16时不同加强筋截面尺寸下的Pc与Pc/WTable 7 Pc and Pc/W under different stiffener section size with 16 meridional stiffeners

综上所述，对于球壳结构，添加加强筋能有效地增大临界屈曲载荷；纬向筋对于P及P/W的影响较为显著，增加纬向筋个数，合理分布纬向筋的位置均能有效提高P与P/W的值；而经向筋的影响则并不明显，需要根据纬向筋的个数合理选择；同时提高梁截面的高度能有效增大P与P/W的值。

3 结论

（1）本文给出了基于ABAQUS的加筋球壳结构参数化有限元模型的建模方法，实现了快速建立不同球壳尺寸和厚度，不同加强筋位置、布局以及截面尺寸的加筋球壳有限元模型，极大地节约了加筋球壳结构设计阶段在有限元建模上所花费的时间，提高了建模效率，为后续的计算及参数分析提供了便利。

（2）提高球壳曲面厚度能够较为明显地提高P和P/W的值；纬向筋对于P和P/W的影响较为显著，增加纬向筋个数，合理分布纬向筋的位置均能有效提高P和P/W的值；而经向筋影响则并不明显，需要根据纬向筋的个数合理选择；增大加强筋截面的高度能有效增大P和P/W的值。因此在对球壳结构进行加筋设计时需要根据实际情况，对上述参数进行仔细设计与选择。

（编辑：马文静）

NIAN Chunbo，WANG Xiaoping，DAI Wenmeng，et al.Analysis of buckling properties of variable angle laminated plates based on secondary development of ABAQUS［J］.Aerospace Materials & Technology，2019，49（4）：17-22.（in Chinese）

［14］JIN Bocheng，LI Xiaochen，MIER R，et al.Parametric modeling，higher order FEA and experimental investigation of hat-stiffened composite panels［J］.Composite Structures，2015，128（C）：207-220.

［15］TANG Jiapeng，XI Ping，ZHANG Baoyuan，et al.A finite element parametric modeling technique of aircraft wing structures［J］.Chinese Journal of Aeronautics，2013，26（5）：1202-1210.