基于同步马达的液压多缸同步提升系统仿真研究

王贵桥，高扬，张福波，孙杰，李建平

(东北大学轧制技术及连轧自动化国家重点实验室，辽宁沈阳110819)

0 前言

同步马达采用多个轴刚性连接的等排量双向液压马达作为等流量分流装置，具有加工精度高、同步性能好、使用方法简单等特点，往往使用开环控制方式就能获得满意的同步精度。因此，在工业现场得到广泛的应用。图1所示为一个典型的四通道同步马达液压回路原理。

但是在某些工况复杂的场合，由于马达出口至液压执行机构之间的特性差异较大，仅仅依靠开环的液压同步马达控制方式，难以获得令人满意的同步精度，并且随着设备在运行过程中的磨损(包括同步马达的磨损和液压执行机构的磨损)，同步精度会越来越差。为了解决上述问题，本文作者首先利用SimHydraulics建立了基于同步马达的四缸同步提升回路模型，并进行了仿真研究，利用控制变量法确定了影响同步马达同步精度的主要因素，在此基础上提出一种基于均值偏差进行流量补偿的控制策略，并对控制策略的有效性进行了仿真验证。

1 仿真模型的建立

SimHydraulics是MATLAB平台的一个液压动力与控制系统的工程设计与仿真的建模环境，是基于Simscape建模环境的物理网络方法。它包含一个综合性的液压模块库，扩展了基本的液压、电气、一维平移和旋转机械元件和实用块。本文作者在Simulink中调用SimHydraulics模块库对图1所示液压回路进行建模，模型如图2所示。

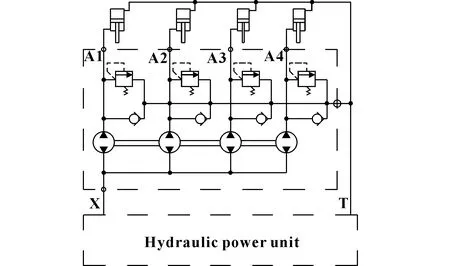
图1 同步马达控制液压原理

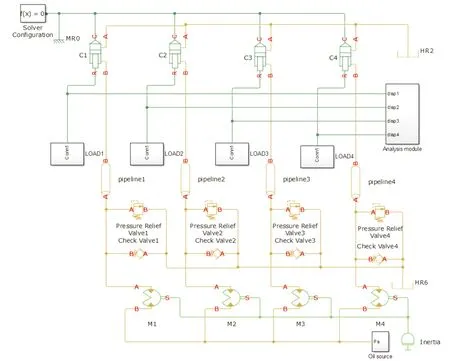
图2 同步马达回路模型

2 仿真实验

2.1 同步误差的定义

假设4个液压缸的位移分别为、、、，液压缸行程均为，液压提升过程中的同步效果反映在4个位移的差异上，差异越小，同步效果越好，设同步误差为，且定义同步误差的大小等于4个位移值最大值同最小值的差与液压缸行程的比值，即

=[max(,,,)-min(,,,)]×100

(1)

2.2 同步马达开环控制仿真

影响同步马达控制精度的因素很多，主要表现在液压管路的布置形式以及液压缸所受的负载不均、不同马达单元之间的差异(排量和内泄系数)。本文作者利用控制变量法，分别研究管路长度、负载质量、单元马达排量、单元马达内泄系数对同步精度的影响。假设基准参数为：管路长度为10 m，负载质量为1 000 kg，单元马达排量为5×10m/rad，内泄系数为1×10m/(s·Pa)。

2.2.1 管路布置形式对同步精度的影响

不计弯头、变径等局部损失的影响，只考虑马达单元出口至液压缸有杆侧之间的管路长度不同，如表1所示，其他参数相同。

表1 不同管路长度

液压缸行程为300 mm，全程平均速度达到100 mm/s，其同步误差仿真曲线如图3所示。可见：当管路布置差别不大时，同步马达能够获得较好的同步效果，同步误差约为4.53%；当管路布置差异较大时，同步马达的同步控制精度受到很大的影响，同步误差达到11.8%。原因在于管路内的液压弹簧刚度差异较大，造成高压条件下油液的压缩体积差异较大。因此，单独用同步马达进行同步控制时，须尽量将各液压执行机构的中间管路对称布置。

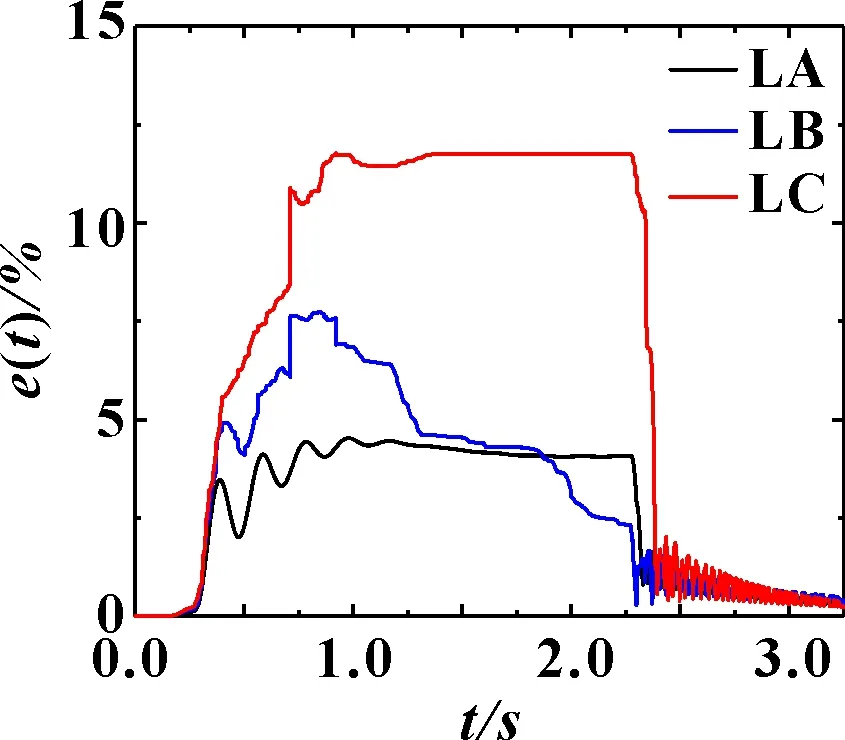
图3 不同管路长度下的同步误差

2.2.2 负载质量对同步精度的影响

只考虑负载质量的差异对同步控制精度的影响，负载模型参数如表2所示。

表2 不同负载质量

仿真结果如图4所示。可见：当负载质量偏差不大时，同步马达能够获得令人满意的同步效果，同步误差约为1.95%；当负载质量差异较大时，同步马达的同步控制精度受到很大的影响，同步误差达到7.82%。原因在于负载质量的不同，造成各管路内的压力差异较大，使得高压条件下油液的压缩体积差异较大；此外，负载的不同对于各元件的内泄差异影响也较大。

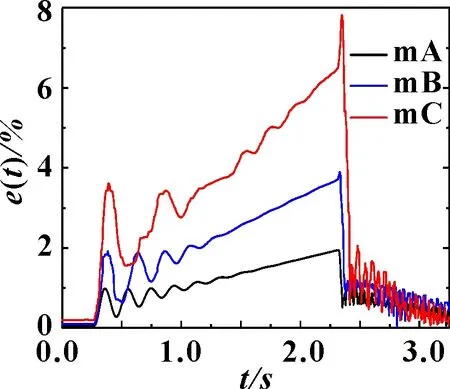
图4 不同负载质量下的同步误差

2.2.3 单元马达排量对同步精度的影响

只考虑同步马达排量,仿真参数如表3所示。

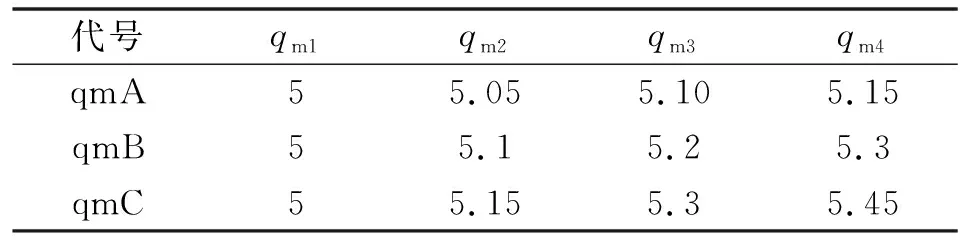
表3 不同马达排量 单位：10-6 m3·rad-1

仿真效果如图5所示。可见：当马达单元间排量偏差不大时，同步马达能够获得令人满意的同步效果，同步误差约为2.95%；但马达单元间排量差异较大时，同步马达的同步控制精度受到很大的影响，同步误差达到8.38%。原因在于排量的不同，相同转速条件下马达排出的油量不同，造成液压缸位移间的同步累积误差。

图5 不同马达单元排量下的同步误差

2.2.4 单元马达内泄系数对同步精度的影响

仿真参数如表4所示。

表4 不同马达内泄系数 单位：10-11 m3·s-1·Pa-1

仿真效果如图6所示。可见：当马达单元内泄漏系数间的差异达到45%时，同步误差约为0.923%，未超过1。因此，马达单元的内泄漏系数差异对同步控制效果影响不大。原因在于马达的内泄漏相对于马达排量来说属于小量，对位置同步误差影响较小。

图6 不同马达泄漏系数下的同步误差

综上，仅仅依靠同步马达，欲达到较高的位置同步控制精度，需要同时保证液压管路的对称布置、较高的负载均匀性以及较高的马达单元加工精度。其中，精密马达单元机械加工成本高，且随着马达单元的磨损精度逐渐难以保证。而较好的液压管路布置对称性及负载布置均匀性受制于复杂的现场条件及工艺设备结构要求而往往难以实现。因此，单纯依靠液压同步马达，在条件相对复杂的工业现场难以实现高精度位置同步的控制，有必要对马达单元通道间的差异产生的同步误差进行有效补偿。

3 流量补偿阀动态补偿控制策略及仿真研究

3.1 电磁阀动态补偿液压回路设计

在液压系统中，为了获取高精度的控制效果，通常采用伺服阀或比例阀进行控制。伺服阀或比例阀能够实现模拟量的连续调节，但其电气控制系统复杂、液压阀抗污染能力差，且价格昂贵。本文作者提出了一种基于同步马达的电磁换向阀动态补偿液压回路，如图7所示。直流电磁换向阀具有换向特性好、工作可靠性高、电气控制简单、价格低廉等优点。

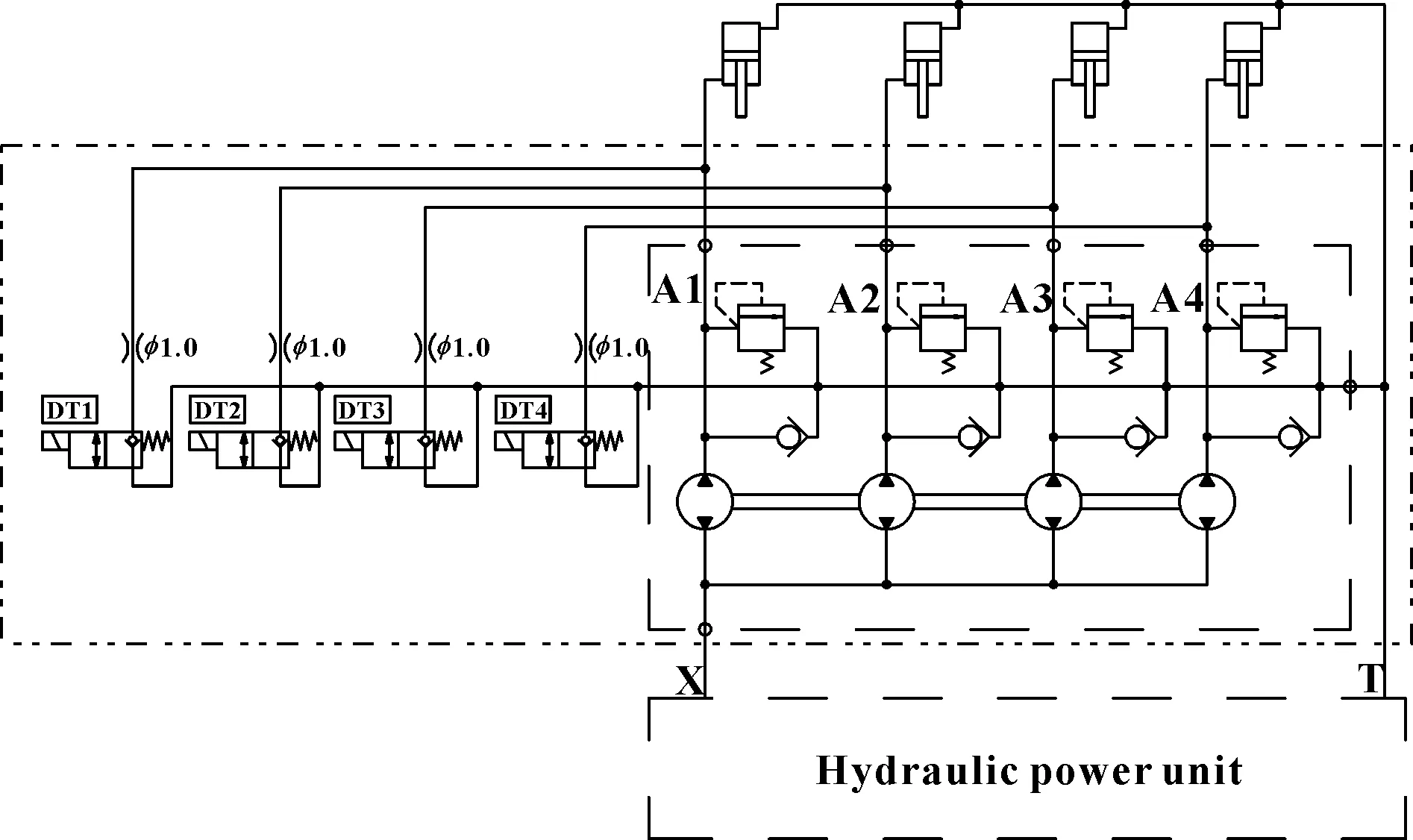
图7 同步马达配合电磁换向阀的同步控制液压原理

3.2 控制算法

4个电磁换向阀通过PLC数字量输出模块连接固态继电器进行控制，整个控制过程都在某循环中断中实现，根据两位两通电磁滑阀的开闭特性，循环中断周期选择为40 ms，其控制流程如图8所示。其中，～分别对应于Ⅰ～Ⅳ区框架位置的辊缝值；代表辊缝平均值；～分别代表与～的差值；～分别代表PLC对图7中各电磁铁线圈DT1～DT4的开关量输出值；代表死区大小，取=1 mm；fun为计算开关量输出值的函数。其算法流程如图9所示，其中：表示函数fun的输入变量，out表示fun的输出值；fun().out～fun().out分别表示函数fun()～fun()的输出量out。流程图当中“PLC执行其他任务”指的是PLC执行除液压多缸同步控制之外的其他工作。

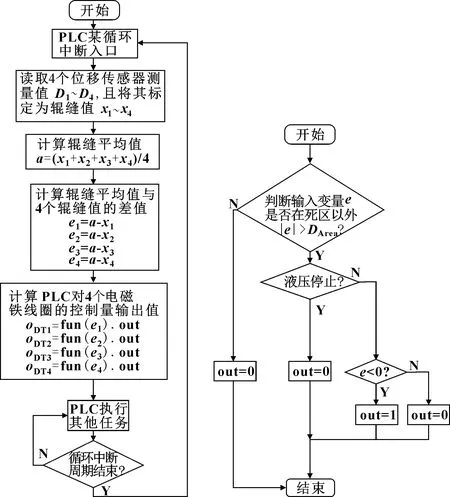
图8 控制流程 图9 函数fun的运算流程

3.3 控制策略仿真

将电磁换向阀加入图2所示Simulink模型，并利用图8—图9所示的控制算法，得到图10所示的模型，并对控制策略进行Simulink仿真分析。

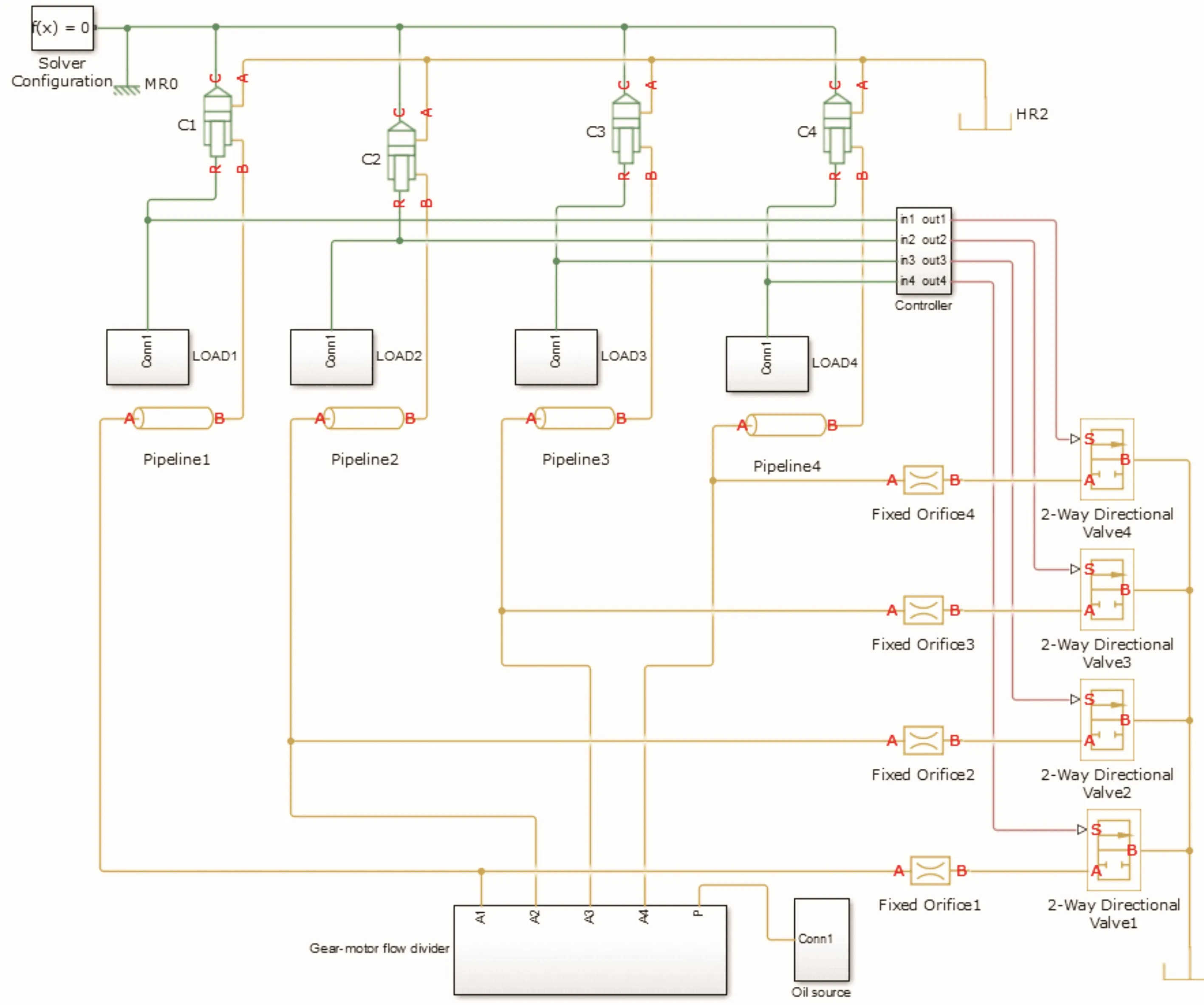
图10 改进方法的控制模型

分别选取表1—表4当中各组参数相差最大的一组参数，利用文中提出的控制策略进行仿真实验，同步误差仿真效果如图11所示。

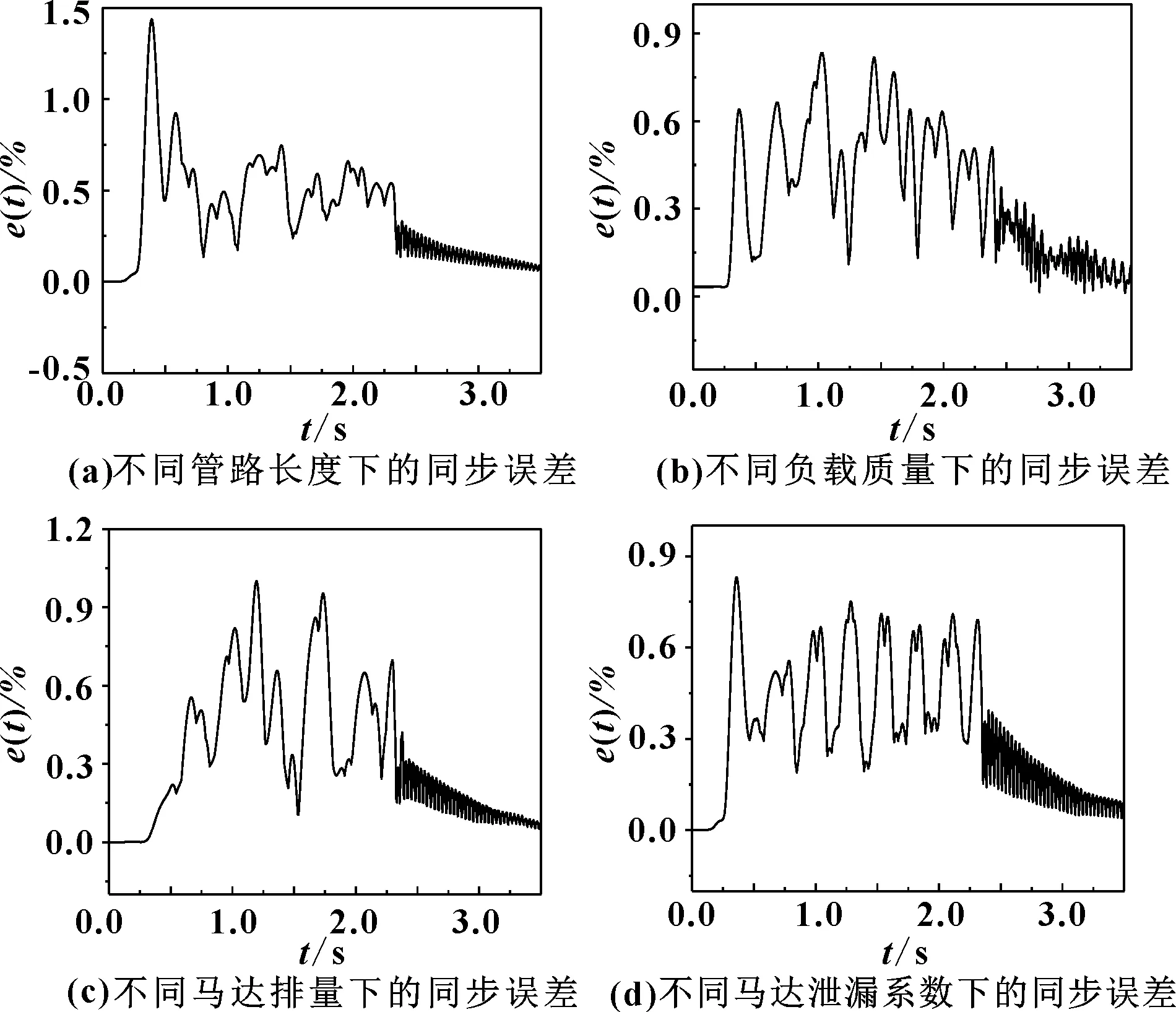
图11 改进方法不同苛刻条件下的同步误差控制效果

可见，相对于单独的液压同步马达控制，加入电磁换向阀进行流量补偿之后，考虑管路长度的影响，同步误差由11.8%减小至1.44%；考虑负载质量的影响，同步误差由7.82%减小至0.833%；考虑排量差异的影响，同步误差由8.38%减小至1.0%；考虑内泄漏系数的影响，同步误差由0.932%减小至0.83%。以电磁阀配合液压同步马达控制策略在各种负载参数或设备参数条件下均获得了高精度的位置同步控制精度。

4 结论

(1)同步马达的控制精度主要取决于马达出口至液压执行机构之间的管路布置对称性、各液压执行机构的负载均匀性以及马达自身的加工制造精度。在工况复杂的工业现场，单纯地采用同步马达实现同步控制，即使马达自身的加工制造精度很高，也会由于液压管路布置不均或者偏载等因素引起较大的同步误差。

(2)采用同步马达配合电磁换向阀进行流量补偿的控制策略，由同步马达实现多液压缸流量的初步分配，然后根据各液压缸运动位移相对于位移均值的偏差进行流量补偿，该方法能够有效地消除由于工况差异所产生的同步位置误差，具有较强的鲁棒性。

(3)提出的电磁换向阀流量补偿策略除了用于同步马达回路，对于节流阀、同步阀等多缸同步场合同样适用，具有广泛的推广意义。