基于模糊物元分析的PSO-LSSVM磨加工补调值在线预测与补偿方法

张志永，郑鹏

(1.郑州科技学院机械工程学院，河南郑州 450064；2.郑州大学机械与动力工程学院，河南郑州 450001)

0 前言

磨削是机械加工中重要的加工方式，磨削精度的高低决定了工件质量的优劣。磨加工主动测量仪是一种能够实时检测工件尺寸，广泛应用于自动、半自动磨床的仪器，其工作原理如图1所示。

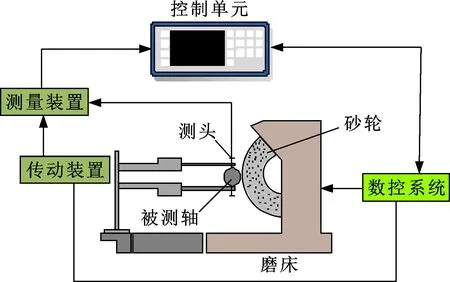
图1 磨加工主动量仪工作原理示意

在磨削过程中，温度产生的温漂会导致系统控制出现偏差,主动测量控制仪动态测量工件也导致偏差的产生；在光磨阶段，光磨余量、砂轮转速、工件转速的设置也会导致偏差的产生。生产现场操作者针对此类偏差，多采用气动量仪测量工件得出偏差值，然后对磨削控制系统信号点设置进行补调，手动输入补调量。此种补调方式滞后于磨削加工进程，且随意性大，主要依赖于操作者的经验。因此在不同批次、大批量的流水线生产过程中依然无法满足自动化的要求。传统的时序预测方法如小波分析、LSTM等因运算过程复杂、预测精度不足等原因，无法满足在线测量的要求。因此，需要寻找更加准确高效的预测方式来提高在线测量磨削过程中的加工精度和加工效率。

磨削工艺参数组合优化对于提高产品加工精度和生产效率至关重要，可利用模糊物元描述方式对磨削工艺参数组合进行快速有效地优化。SUYKENS等利用具有等式约束并满足KKT条件的规则化最小二乘支持向量机函数作为损失函数，提出了最小二乘支持向量机(Least Squares Support Vector Machines, LSSVM)模型，它具有良好的泛化性能、高计算效率和高维鲁棒性的优点。将模糊物元分析方法与LSSVM相结合，通过模糊物元分析迅速准确地获得最佳工艺参数，并将对应的参数作为输入训练出LSSVM预测模型。粒子群算法(Particle Swarm Optimization, PSO)是一种源于复杂适应系统的进化算法，从随机解出发，通过不断的迭代来寻找最优解，通过适应度函数来评价解的优劣，具有原理简单、易实现、精度高、收敛快等特点。虽然LSSVM算法具有良好的线性回归拟合和统计预测能力，但在计算过程中容易陷入局部最优解，使得LSSVM算法的线性回归和统计预测能力受到影响。因此利用PSO对预测模型进行参数寻优，在保证模型准确率的同时，可提升模型的泛化程度。补调值预测补偿反馈控制示意如图2所示。

图2 补调值预测与补偿反馈控制示意

1 基于模糊物元分析的PSO-LSSVM补调值在线预测模型

1.1 模糊物元分析

物元分析理论中要求用“事物、特征和量值”对事物属性进行描述。若模型中的量值具有不确定性，可称为模糊物元，若有个事物、、…、,用其共同的个特征、、…、及其相应的量值1、2、…、，则称为个事物维复合物元。一般计算中，可用量值代替模糊量值，构成复合模糊物元，记为。

(1)

利用模糊物元描述方式，并使用模糊集合和关联度评定的方法，将灰色关联法计算所得的客观权重和层次分析法所得的主观权重进行复合，兼顾实验数据逻辑性和决策可参与性，可很好避免权重分配不合理之处。将2种改进方法结合，可实现对磨削工艺参数组合进行快速有效的优化。

1.2 PSO-LSSVM预测模型构建

设粒子群大小为，单个粒子维数为，即对维空间(1,2,3,…,)进行搜索，表示第个粒子。第个粒子的速度可表示为=(1,2,3,…,)(=1,2,…,)；第个粒子的历史最优解为=(1,2,3,…,)(=1,2,…,)；粒子群的全局最优值为=(,,,…,g)。其速度和位置更新公式为

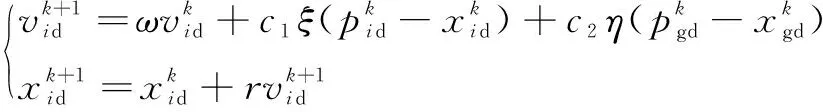
(2)

其中：为惯性权重，是用于保持原速度的系数；、分别为个体最优值的权重系数和群体最优值的权重系数，通常都设置为2；、都是[0,1]区间内的随机数；系数称为约束因子，通常设置为1。适应度函数是度量粒子当前位置与全局最优位置之间距离的函数，文中将磨加工补调值预测值的均方根误差作为各个粒子的适应度函数，距离全局最优位置越近的粒子，其适应度函数值越小。适应度函数的表达式为

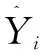
图3 LSSVM分类和回归示意

假设样本集={(,),=1,2,…,}，对于LSSVM，(,)是样本的输入和输出变量，∈,∈。存在一超平面·()+=0，这个超平面可以将所有样本分开。LSSVM的分类和回归模型如图3所示，是超平面的法向量，是其中常数。补调值的预测是非线性问题，需要通过一个核函数将输入向量从低维空间映射到高维特征向量空间，转换为线性可分的数据。在高维特征空间对数据构造分类超平面，将映射为高维空间的()，即→()=[(),(),…，()]，根据希尔伯特-施密特原理，将原来线性情况下的内积运算替换成()·()即可。LSSVM利用()=·()+进行估计，式中(·)将输入从低维非线性映射为高维线性，把非线性问题转化为高维特征空间中的线性拟和问题。LSSVM的优化问题为式(3)，其中为惩罚参数，决定了函数的光滑程度。

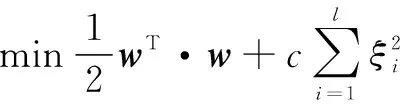
(3)

约束条件公式如下：

[·()+]=1-=1,2,…,

(4)

构造拉格朗日函数进行求解：

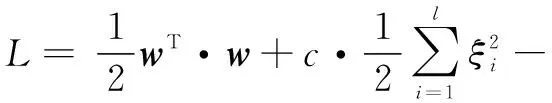
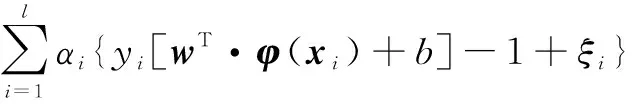
(5)

其中，为拉格朗日乘子。根据KKT条件，得到如下等式约束条件：

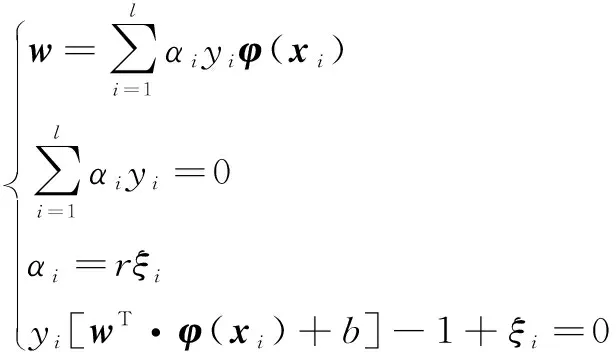
(6)

对于=1,2，…，，通过式(6)消去和，式(7)为经过解算推导出的LSSVM最优超平面公式，使用该式可训练磨加工时输入的尺寸数据。

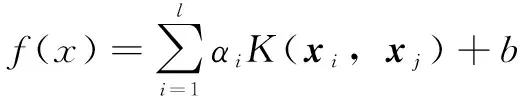
(7)

其中核函数(,)即为某一空间内积()·()，因高斯核函数具有较少的核参数，模型的复杂程度较小，故核函数选用高斯核函数，公式如式(8)所示，其中为核参数。

(,)=exp[-(-)(2)]

(8)

在高斯核函数中，太小会导致过拟合，过大会影响判别函数的分布。核参数与惩罚参数共同决定了分类超平面的位置和形状，它们取值过大或者过小都会影响LSSVM预测模型的泛化程度。故采用PSO对LSSVM的核参数和惩罚参数进行优化，提高LSSVM算法的线性回归拟合和统计预测能力。设置粒子群数量，初始化粒子群参数、、、和循环次数，初始化核参数和惩罚参数。根据各个粒子位置坐标(，)，构建其对应的LSSVM预测模型，并对磨加工补调值进行预测。根据各LSSVM模型的预测结果，计算各LSSVM模型的预测误差，并将它作为粒子个体适应度值。保存适应度值最优的粒子个体位置坐标(，)，更新各粒子个体的位置坐标(，)，根据更新后的(，)重新构建LSSVM预测模型，并对磨加工补调值进行预测。根据LSSVM模型的预测结果，重新计算各个LSSVM模型的预测误差，确定适应度值最优的粒子个体位置坐标(，)。判断是否满足结束条件，若不满足则循环执行上述操作，若满足则根据适应度值最优的粒子个体位置坐标(，)，构建LSSVM预测模型并对磨加工补调值进行预测，完成磨加工补调值预测目标。PSO优化LSSVM模型流程如图4所示。

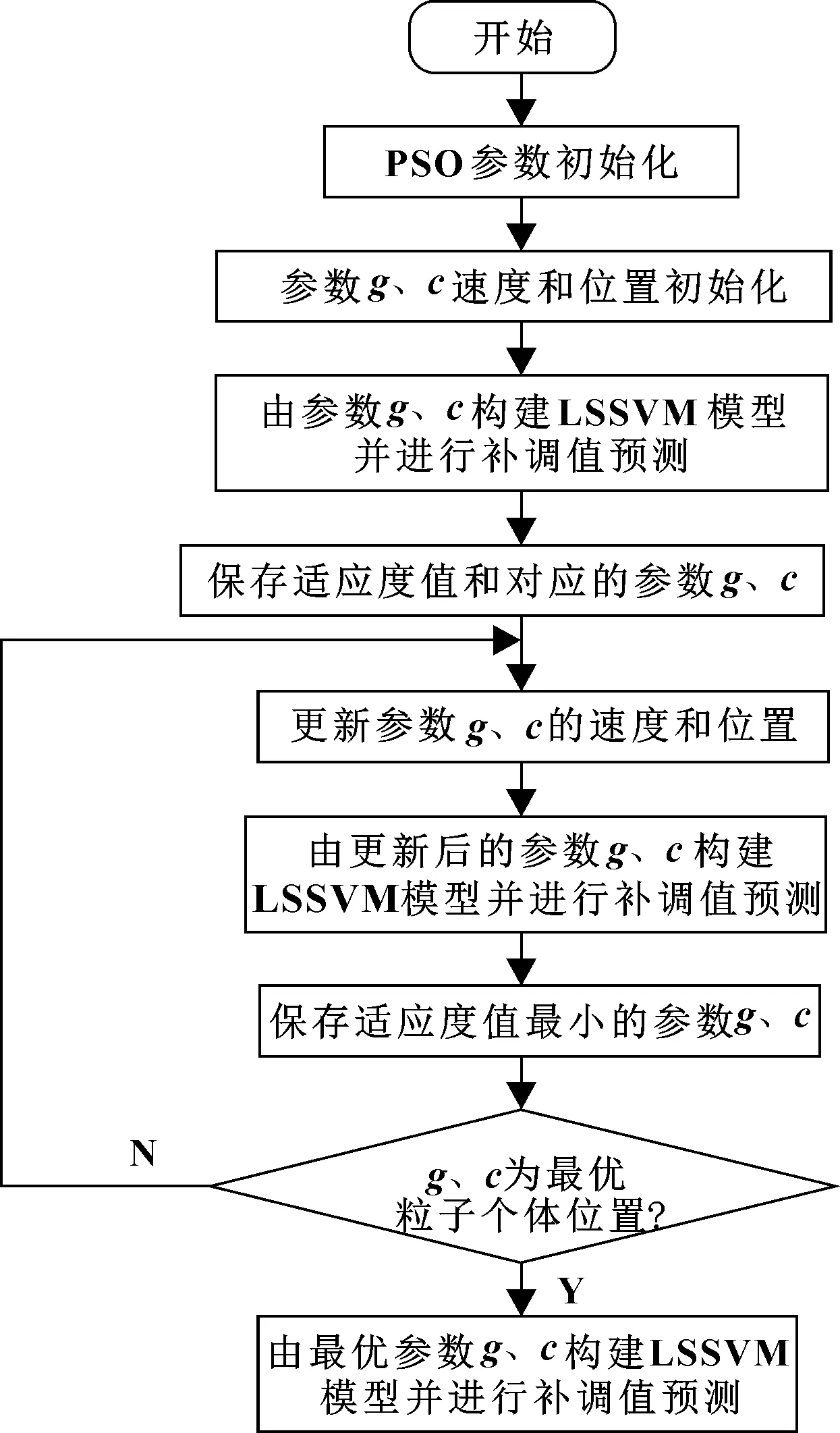
图4 PSO优化LSSVM模型流程

1.3 补调值在线预测与补偿实现流程

利用模糊物元理论优化磨削工艺参数，将寻得的最优工艺参数组合输入LSSVM补调值预测模型，采用PSO对预测模型中高斯核函数的核参数和惩罚参数进行优化。具体的磨削补调值在线预测与补偿步骤如下：

(1)原始数据预处理，构建样本数据，包括数据的粗大误差剔除、数据的均值化、归一化。

(2)利用模糊物元理论得出最优工艺参数组合。

(3)构建LSSVM补调值预测模型。预测模型训练样本集合为(,)(=1,2,…,)，为输入值，是一个由组参数构成的维向量，即模糊物元理论得出的最优工艺参数组合；为相应的补调值。

(4)对模型作训练学习，同时用PSO参数优化方法对预测模型参数寻优，选取最优参数。

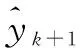
图5 补调值预测与补偿实现流程

2 基于模糊物元分析的PSO-LSSVM磨加工补调值在线预测与补偿实验

2.1 磨加工主动量仪在线测量加工进程分析

在磨削加工过程中，当预测尺寸超出误差允许范围边界时，向数控控制系统发出补调指令。控制系统接收指令后，通过更改工艺参数对误差进行补调。砂轮进给机构和驱动装置根据指令调整，实现工件尺寸闭环控制。利用在线测量进行磨削加工时，需要根据工艺规程设置特征点。加工进程被特征点划分为5个阶段：快速进给阶段()-粗磨加工阶段(-)-半精磨加工阶段(-)-精磨加工阶段(-)-光磨阶段(-)，如图6所示。

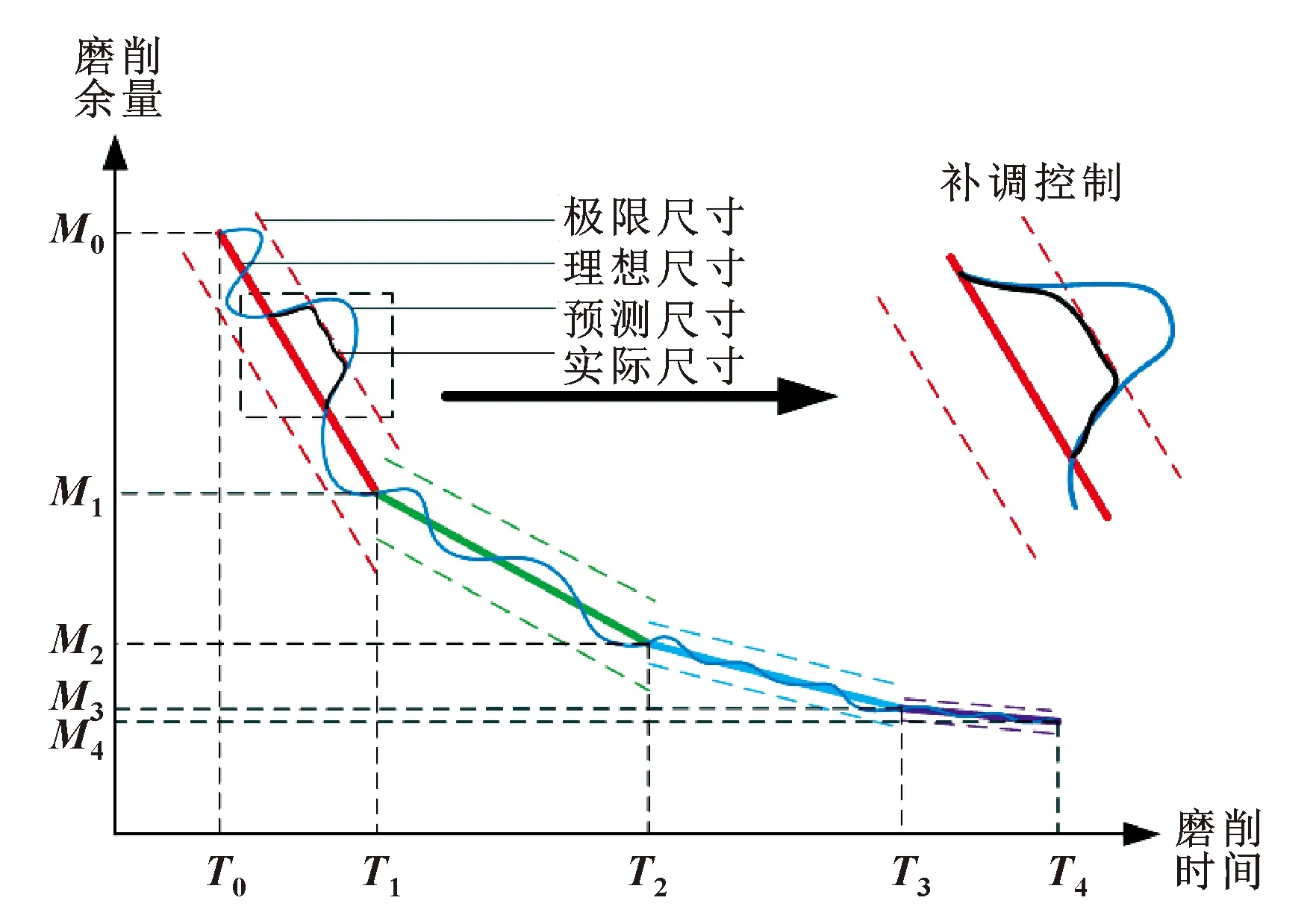
图6 加工进程

测量装置在快速进给结束时刻启动，此时机床执行粗磨加工。当控制单元检测到工件尺寸达到各阶段尺寸要求时，数控系统自动调整工艺参数进入下一磨削阶段，直至工件满足设计要求(切断点)，砂轮执行回程运动直至下一循环开始。由于精磨和光磨阶段对加工质量影响明显，故选择精磨和光磨阶段尺寸数据进行实验。

2.2 实验验证与分析

为验证基于模糊物元分析的PSO-LSSVM磨加工补调值在线预测与补偿方法的有效性和准确性，设计并进行了在线测量磨削加工实验。实验装置选择高精度外圆磨床MGB1320E，磨削工件材质为45钢，采用外圆径向切入方式进行小批量磨削实验，如图7所示。

图7 实验装置

由模糊物元分析可得最佳工艺参数组合如表1所示，采用该组工艺参数对工件进行加工。共进行35组实验，每组加工20个工件，加工后工件尺寸采用气动量仪测量，测量时每个工件选择5个测量点，去掉极大值和极小值，取剩余3个值的平均值为尺寸实测值。通过求取实测值与公称值之间差值得到补调值的实测值，可有效地去除测量偶然因素的影响。对采样值误差作均值处理，对每组实验数据求均值，得每组的尺寸平均实测值、平均补调值，使得建模数据尽可能地拟合真实磨削数据。

表1 最优工艺参数组合

记录每次磨削过程中各阶段的尺寸数据用于预测模型训练，并将训练完成的模型应用于在线测量加工，验证以预测值进行补调的磨削加工结果。程序均采用MATLAB编制。进行补调值预测时，采用PSO对LSSVM补调值预测模型参数寻优，得最优参数=0.615 5、=24.251 4。图8所示为采用试样内35组数据训练所建立模型的参数和优化结果示意。图中横轴与纵轴分别表示和取以2为底的对数后的值，竖轴表示对应的预测精度，文中选用适应度函数值即均方根误差作为评判准则。

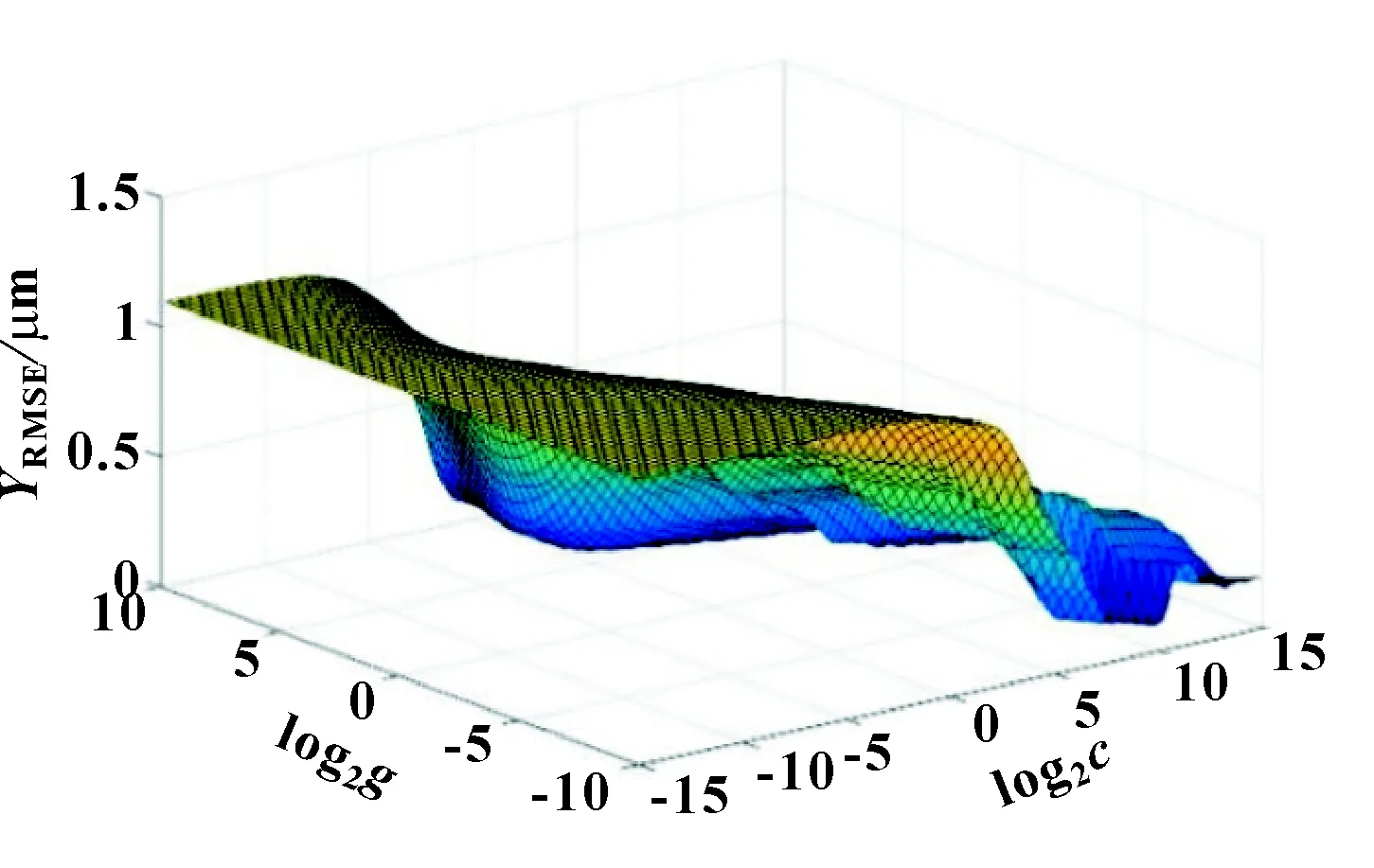
图8 PSO模型参数优化结果示意

表2为外圆磨削试验补调值的实测值与预测值。补调值预测模型预测精度与稳定性的优劣采用平均绝对误差(Mean Absolute Error,MAE)与均方根误差(Root Mean Squared Error,RMSE)来评判，计算公式如下：

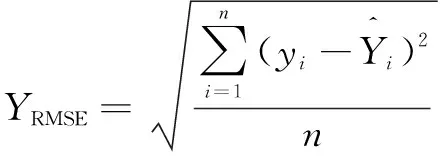
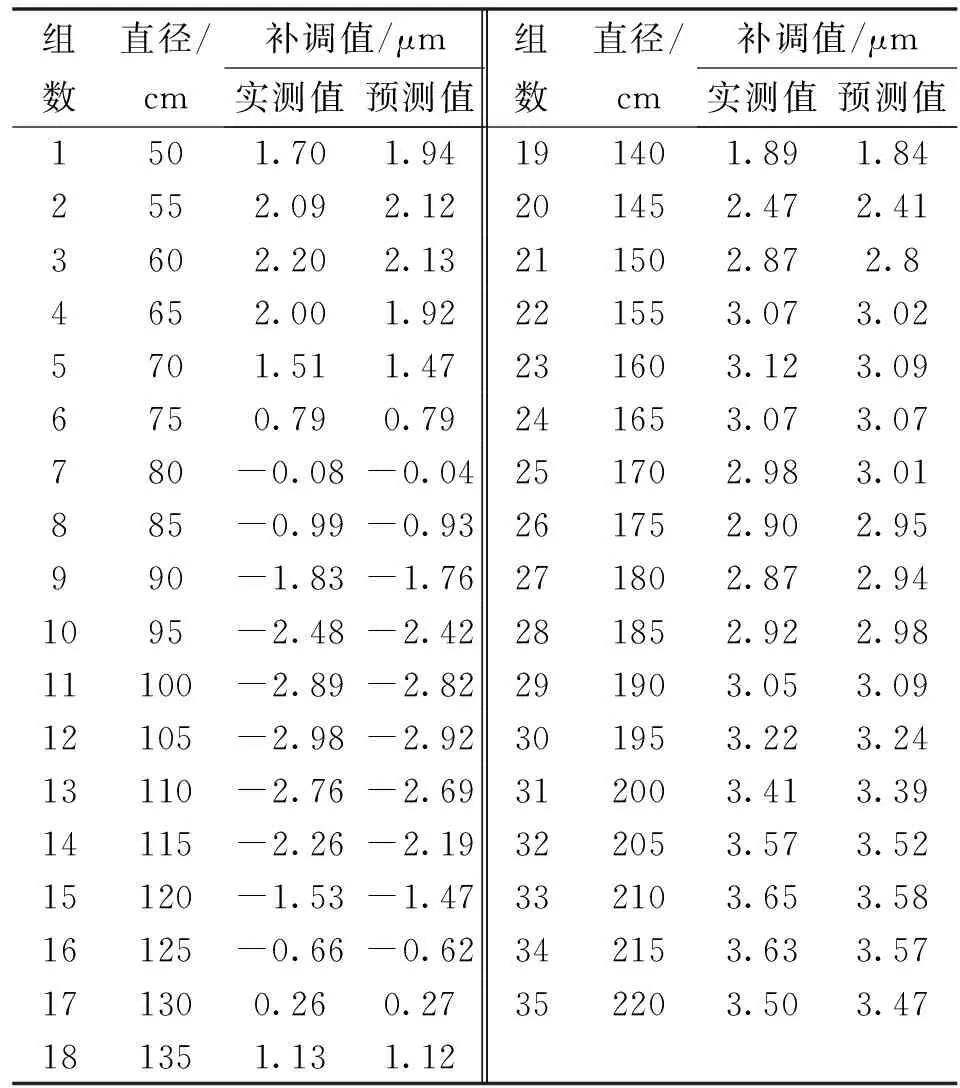
表2 工件外径尺寸补调值实测数据及预测值

模型的与值越小，表示模型预测精度与稳定性越高。通过计算可得:预测模型获得的补偿值与实际应补偿值的平均绝对误差为=0.052 57 μm，均方根误差=0.065 33 μm。图9所示为补调值预测值与实测值对比曲线。

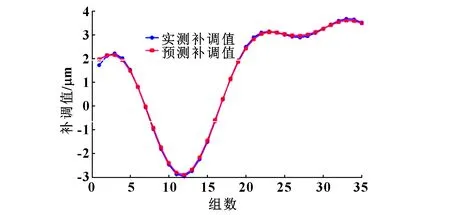
图9 样本内预测补调值与实测补调值对比

只采用样本内数据验证模型的精度时，会出现忽略过学习、泛化性弱、推广能力不强的问题，难以确保模型的普适性。用所得补调值预测模型对试样以外的批量工件进行外圆磨削加工实验，分析模型对此补调值的预测精度，通过判断预测精度能否达到主动测量控制仪的要求，来判断模型的普适性。样本外磨削试验进行了8组，参数寻优得最优参数=6.498 0、=3.249 0，如图10所示为采用样本外8组数据训练所建立模型的参数和优化结果示意，表3所示为磨削补调值实测值与预测值。

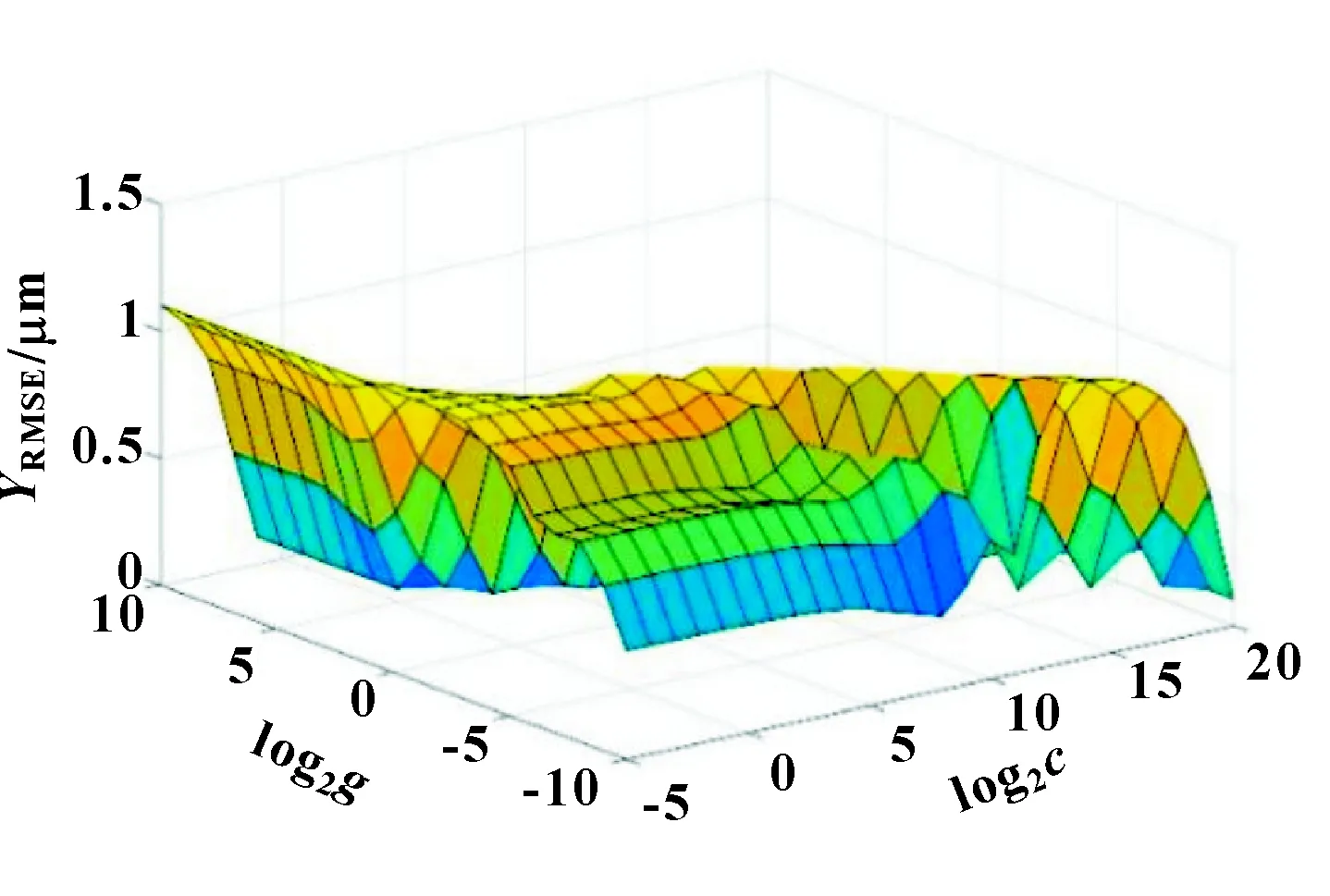
图10 PSO模型参数优化结果示意

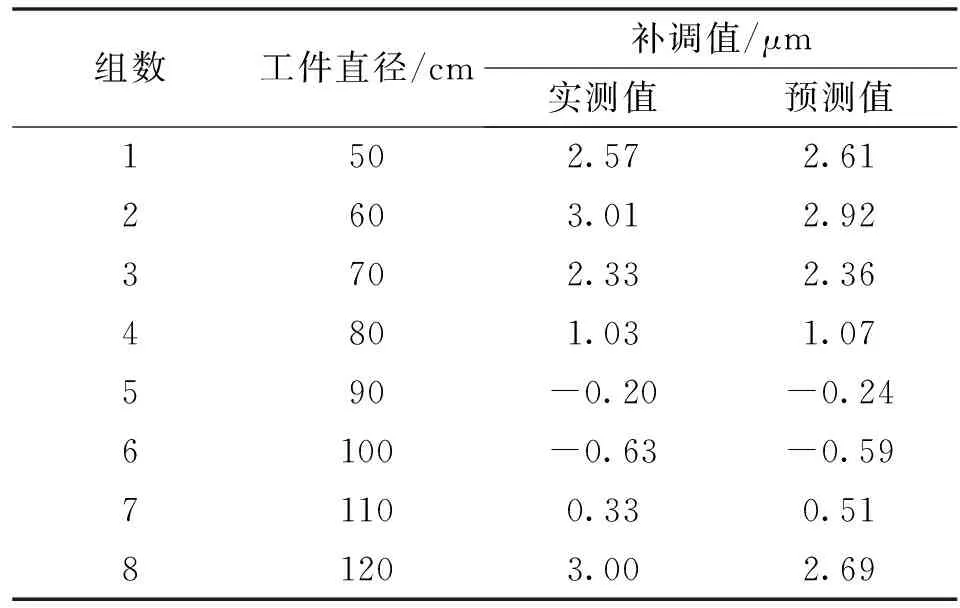
表3 磨削补调值实测值与预测值

预测结果表明：预测模型对试样外的工件磨削补调值进行预测时，模型训练样本平均绝对误差=0.096 25 μm，均方根误差=0.134 12 μm。图11所示为训练样本外补调值预测值与实测值对比。

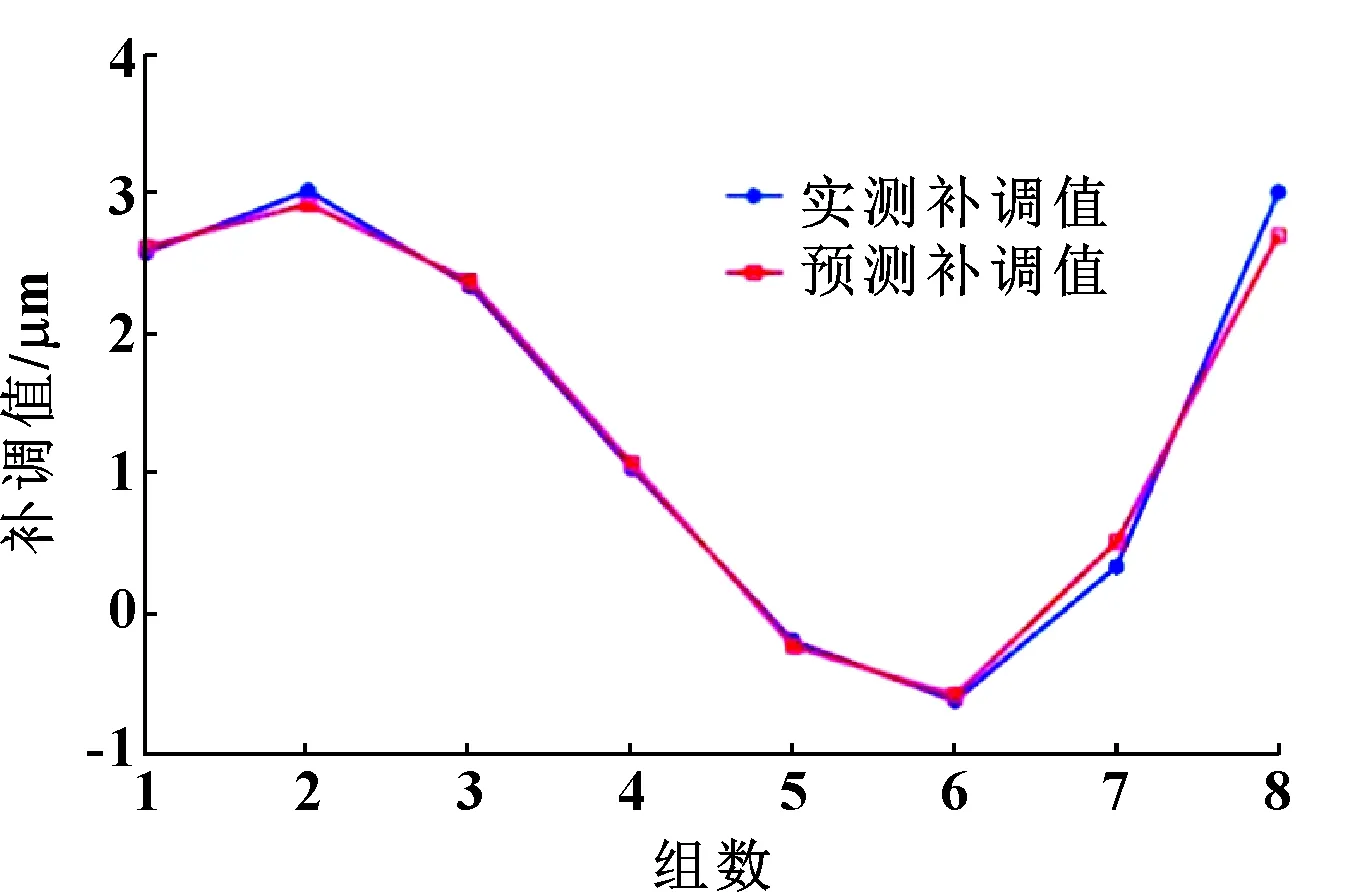
图11 样本外预测值与实测值对比

将补调值预测模型应用于外圆磨削误差反馈补偿系统中，将模型预测所得补调值反馈到主动测量控制仪，在线控制磨削补调值的设置，加工一批工件尺寸为100 mm的柱状工件，光磨余量定为7 μm，温度为20 ℃，工件转速为105 r/min，砂轮转速为38 m/s。分析在误差补偿反馈控制情况下加工工件的精度。图12所示为批量工件的尺寸分布。由统计结果可知：增加补调加工之后相对误差的平均值和方差均有明显提高，表明利用该预测模型进行在线预测和补调加工可有效提高加工精度。同时相对误差的分布接近正态分布，表明该方法具有良好的重复性和较高的应用价值。

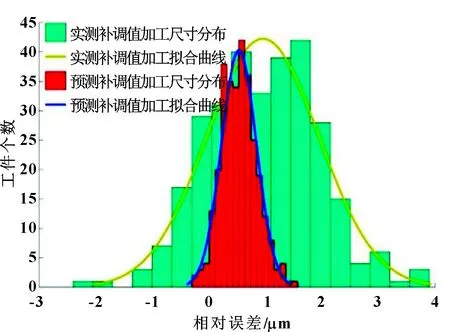
图12 批量工件加工误差分布

3 结论

针对现有磨削加工主动测量过程需要人工手动补调导致随意性大、实时性差等问题，通过对磨削过程的分析和预报理论研究，提出了基于模糊物元分析的PSO-LSSVM补调值在线预测与补偿模型，通过试验验证得到预测模型对试样内以及试样外的工件补调值预测精度高，符合补调值预测的精度要求。将模型应用于磨削加工时，对补调值作预测并及时反馈给磨床控制系统，实现自动调节工艺参数设置。研究成果有效地提高了产品加工精度的一致性和加工效率，对提升磨削加工智能化水平具有积极意义。