基于大数据背景下时间序列的用电量预测模型构建

姚长征，张自强，李玉杰，王选岐

(1.国网庆阳供电公司，甘肃 庆阳 745000；2.国网甘肃省电力公司，甘肃 兰州 730000)

目前而言，居民用电量预测仍然是电力系统最为关注的研究课题之一，准确的居民用电量预测同时有益于电力公司与普通居民。对电力公司来讲，可以规范运营策略，提升服务质量，降低营销成本；对普通居民来讲，有助于规划用电计划，购买合理的用电套餐，达到随时随地可监控自己的用电量的效果。因此，居民用电量预测研究很有必要，其为电网规划建设、市场开拓、台区三相负荷不平衡调整等提供科学的依据支撑。

国内对用电量的预测研究大部分都停留在回归分析等传统方法，该方法预测精度不高，并且对变化趋势反映迟钝。近几年，有些学者提出了数据挖掘算法如神经网络等进行居民用电量预测，但该方法要求样本具有高的代表性，并且解释过程相对困难，针对上述方法的不足，本文采用较为简单的时间序列算法对居民用电量预测研究，利用描述性统计对居民用电量敏感度进行了分析。实现对居民用电量的精准预测，提升电力公司的服务质量，降低95598关于居民用电量的投诉量，为营销居民用电管理提供决策参考利用居民日电量数据汇总生成县区日电量数据，结合气象数据，分析居民用电气象敏感度，达到预警的作用。

1 数据挖掘分析

1.1 数据来源

本次分析电力内部数据取自营销业务应用系统、用电信息采集系统，取数粒度到居民用电客户层级，数据周期为2018年1月至12月，总数据量约1.02 GB、数据记录总数约7.19亿条。

1.2 数据质量

(1)可信度：日冻结电量来自于用采系统，为一次数据，具有较高的可信度。(2)完整性：日冻结电量因采集原因不存在重复情况，存在少量数据项缺失情况，整体字段完整度较高，不影响后续的数据挖掘分析。(3)数据质量：日冻结电量主要存在数据为空或电量数值突变的情况。

1.3 数据预处理

对日冻结电量数据为空或数值幅度突变的情况，使用该数据临近数据平移填补；将12个月度日冻结电量宽表合成年度日冻结电量宽表，如图1所示。

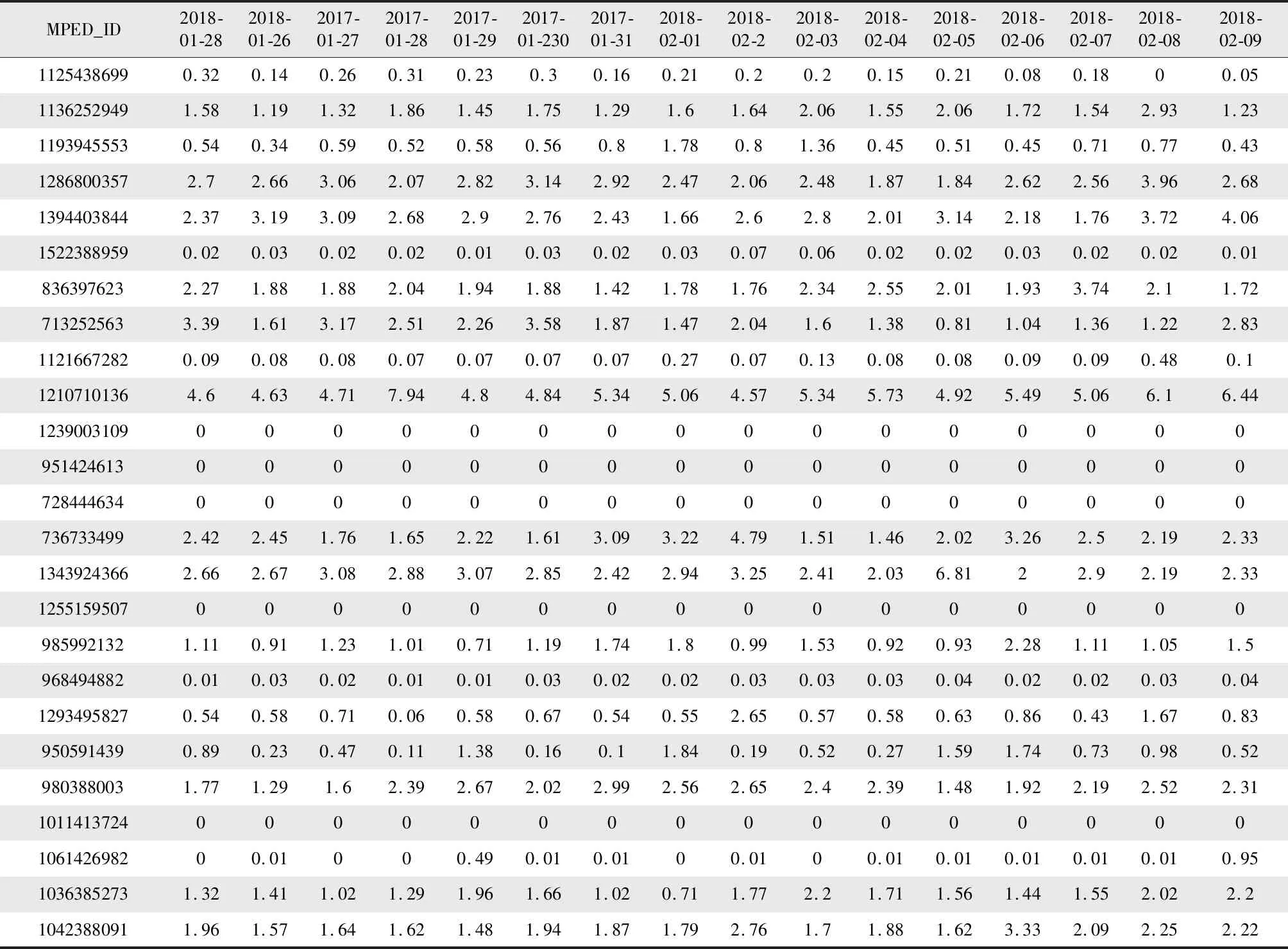
表1 年度日冻结电量宽表Tab.1 Annual daily frozen power meter

根据数据集中的用户日电量汇总计算周电量、月电量、供电所日电量、县区日电量。

居民个人日电量曲线波动大，外界影响比较显著。为减小外界因素影响、提高模型可行性和预测精确度，将用户按照所属供电所分类后，使用日电量求和计算得到的供电所每日用电量进行预测。

1.4 模型构建

由居民日用电量按照居民所属供电所计算供电量日用电量，基于3次指数平滑算法对未来一周的日用电量进行预测，在确定最佳参数后，确定向后预测3 d效果最佳。

算法选择

几种算法比较，结果如表2所示。

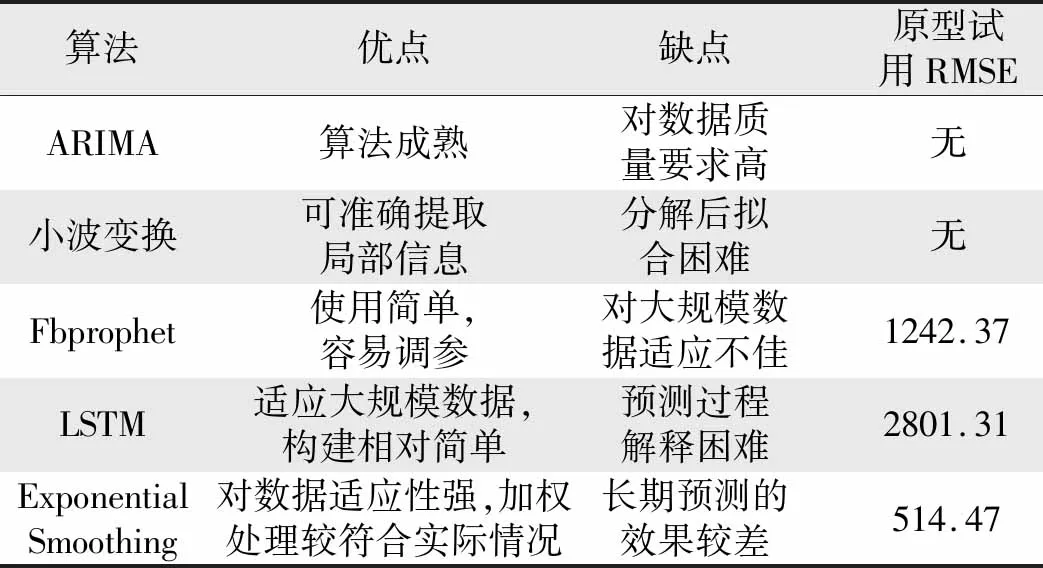
表2 算法比较Tab.2 Comparison of algorithms

由表2可知，ARIMA要求数据既具有平稳性又非白噪声，部分数据无法满足需求，故而无法预测，试用阶段未完成计算；小波变化先将数据分解，分解得到的数据分别拟合、预测，最终将各个预测结果合成，过程复杂，且分别拟合效果不佳，试用阶段未完成计算；Fbprophet虽完成计算，但计算时间长，对大规模数据适应性不好，总体效果在完成计算的3种方法中最差；LSTM、ExponentialSmoothing适应大规模数据，计算时间短，比较RMSE(均方根误差)可知，ExponentialSmoothing更低，故最终选择ExponentialSmoothing算法。

算法介绍

通常3次指数平滑算法分为累加和累乘2种方式，在本研究中使用累加形式的3次指数平滑算法，其用公式表示为：

=(--)+(1-)(-1+-1)
=ß(--1)+(1-ß)-1
=(-)+(1-)-

式中：为周期。

累加3次指数平滑的预测公式为：+=++-+(mod)，其中，，是平滑参数，是之前个数据的平滑值，变量来表示平滑后的趋势，是指“周期性”部分，是这个周期的长度。

参数训练

3次指数平滑的主要参数有：smoothing_level(alpha值)、smoothing_slope(belta值)、smoothing_seasonal(gamma值)参数使用网格搜索调参。指数平滑算法中alpha值代表最近的历史数据对预测结果的影响，考虑到用电量预测最近的历史数据与未来相似程度最高，所以alpha值至少在0.9以上。本研究鉴于均方根误差最小来确定最终参数值，当smoothing_level为0.99，其余2个参数为None时效果最佳，其RMSE值最小为332.13。

模型调优

在确定模型参数后，计算预测效果最佳天数，使用模型参数向后预测7 d，通过使平均误差控制在一定的范围之内确定最佳预测天数。

经计算，未来7 d的平均预测误差如表3所示。

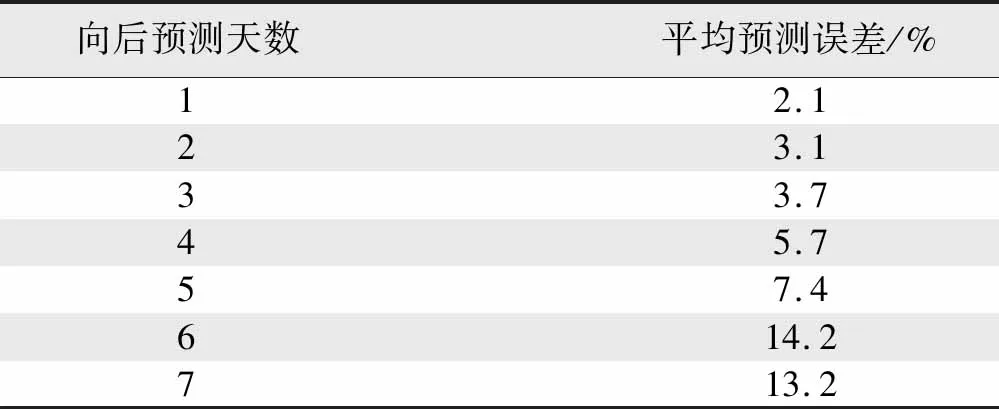
表3 平均预测误差Tab.3 Average forecast error

由平均预测误差可知，前3 d预测误差小于4%，预测精度较高，故选择向后预测最佳天数为3 d。

1.5 居民用电气象敏感度分析

分别分析温度、风力、相对湿度、降水量、极端天气对用电量的影响，最后根据分析结果构建相关图表。

数据处理

数据处理包含2部分：气象数据处理和用电量数据处理。

气象数据处理时间周期为2018年1月1日至2019年6月30日，包含气象、温度、相对湿度、风力、降水等信息，数据集中没有重复值、异常值，但含有缺失值，通过其他形式查找缺失气象数据填补缺失值(如以往的天气预报值)。

用电量数据处理，首先将测量点标识与该表所在区县代码一一对应，然后根据区县代码计算该区县的用电量。

在对气象数据和用电量数据处理完成后，按照对应日期合成宽表。

温度敏感度分析

温度敏感度分析，结果如图1所示。

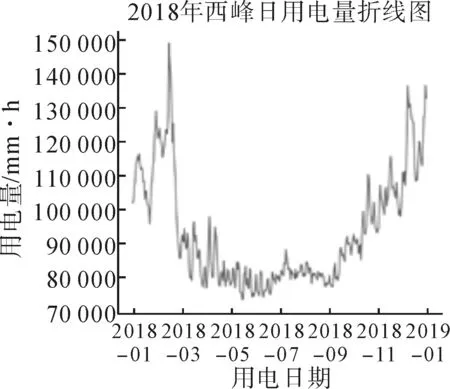
(a)2018年西峰日用电量折线图

从2018年西峰日用电量折线图中可以看出，1～2月份用电量大，且波动明显；3～8月用电量趋势总体略显下降；9～12月用电量总体上升，从11月开始用电量波动增大。这也体现庆阳市的特点，夏季空调降温用电量少，冬季采暖用电量高。

从2018年西峰气温折线图可以看出白天和夜晚温度总体趋势大体相同，都呈现先上升再下降的趋势，为简化分析，只分析其中代表性较强的夜晚温度。夜晚温度折线图中1～2月份、11～12月份温度基本都在0度以下且震动幅度很大，其他月份总起呈现先上升再下降的趋势，其中拐点出现在9月份。

温度和用电量对比分析，结果如图2所示。

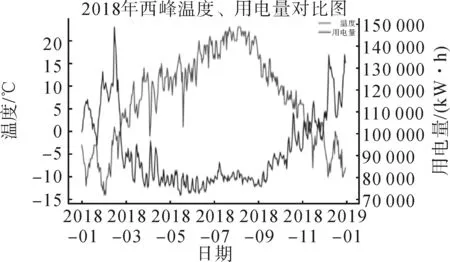
图2 温度和用电量对比分析结果Fig. 2 Comparison analysis results of temperature and power consumption

由图2可知，温度和用电量总体呈负相关关系，部分呈正相关性。

将上述描述推广到庆阳市的各个县，不同区县用电量对气温的敏感度不同，表4为不同区县对温度敏感度的描述(加入阈值)。

用电量受到多种因素的影响，为了重点强调现温度对用电量的影响，选择相关性系数绝对值大于0.8，即对温度敏感度非常高的时间段，分析温度对用电量的具体影响；结果如表5、表6所示。

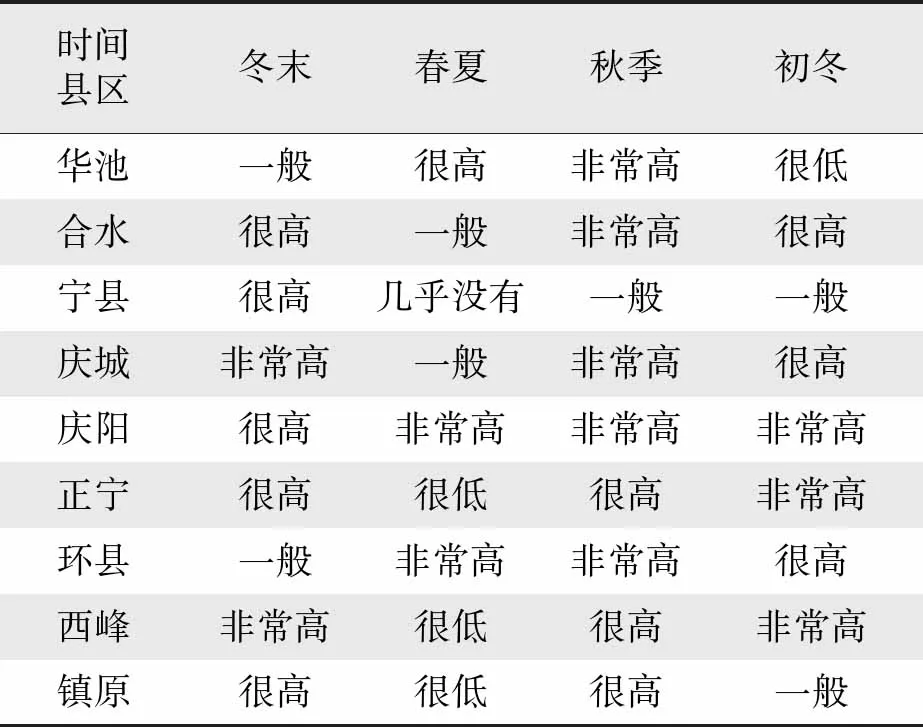
表4 不同区县对温度敏感度的描述Tab.4 Description of temperature sensitivity of different curves

对春夏、秋季2个时段，其变化趋势单一，具体趋势如下：

对冬末、初冬2个时段，其用电量波动性大，同时拥有温度上升时，用电量下降；温度下降时，用电量上升的趋势。

风力敏感度与相对湿度分析

风力敏感度与相对湿度分析，结果如图3所示。

图3 风力敏感度与相对湿度分析结果Fig. 3 Results of wind sensitivity and relative humidity analysis

表5 用电量随温度变化的趋势(春夏、秋季)Tab.5 Trends of electricity consumption with temperature change (spring & summer, autumn)

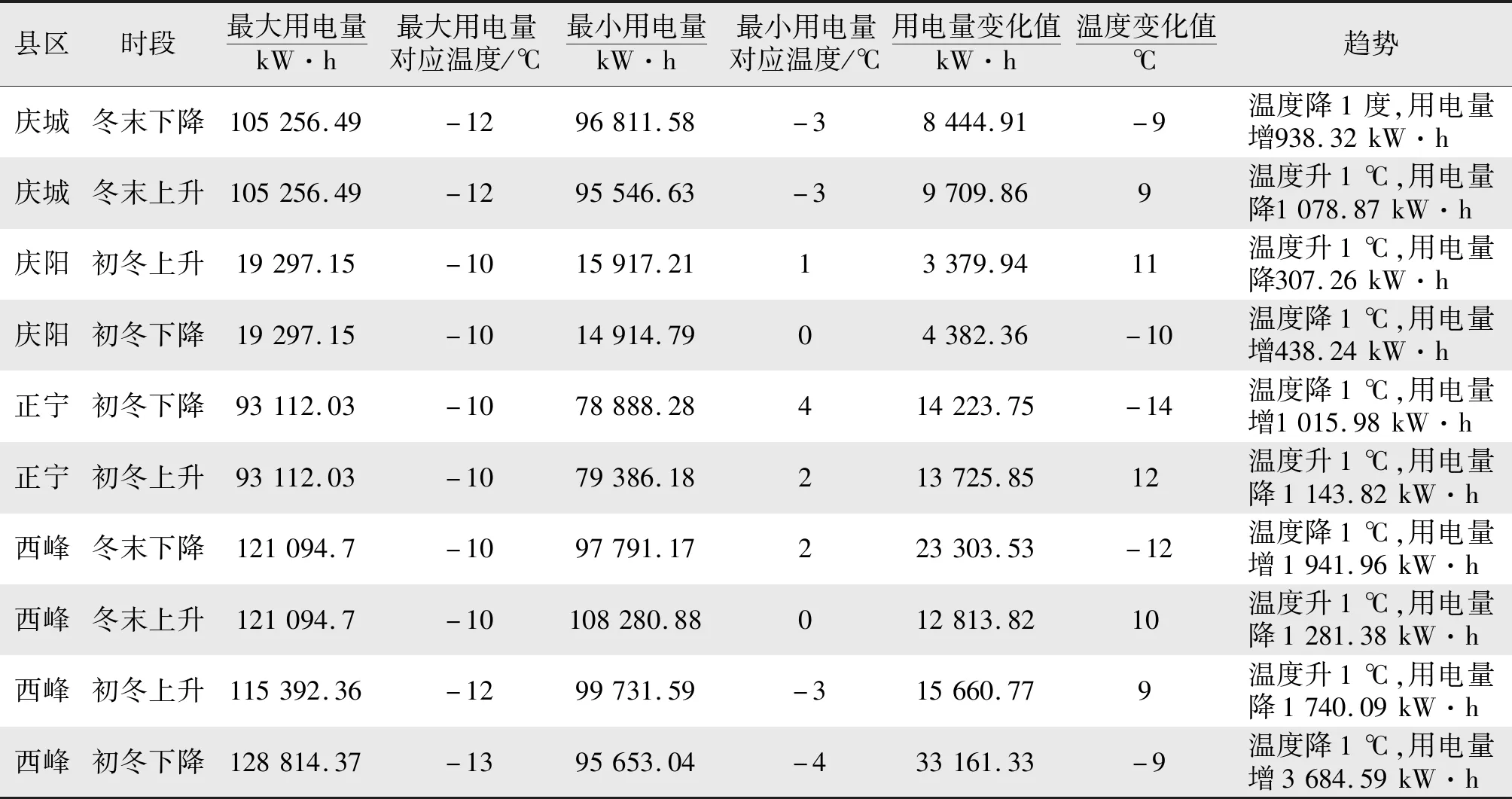
表6 用电量随温度变化的趋势(冬末，初冬)Tab.6 Trends in electricity consumption with temperature change (late winter, early winter)

由图3可知，左边散点图根据某一天与前一天的风力等级、用电量的变化差值构成的；右图根据某一天与前一天的相对湿度、用电量的变化差值构成的。当风力或相对湿度等级增加1级时，用电量既可能增加也可能减少，不存在一定的规律。同样的方法应用到降水量与极端天气变量，可以得到相同的结果。

2 模型应用

基于时间序列的居民用电量预测研究，一方面试点单位的相关管理人员可根据预测结果制定负荷调整计划，最大程度上降低企业运行成本；另一方面电力公司根据温度与用电量大致上呈现负相关的基础上，在温度急剧上升或急剧下降的事件发生时，可以辅助制定应急策略，让气象敏感单位做好提前预防工作，尽可能降低极端事件带来的人力物力损失。同时在应用过程中，可将新的数据作为验证集代入模型，进一步调整模型参数，使模型达到最优。

3 创新点

本研究在传统居民用电量短期预测的研究基础上，进一步研究了居民用电气象敏感度分析，将人为不可控因素作为辅助因素(温度，风力，相对湿度，降雨量与极端天气)加入到居民用电量的研究之中，这种不可控因素无法阻止其发生，但我们可以在不可控情况发生时，及时提出相应的策略，达到预警的作用，这样既能完善电力系统功能，又能提升居民客户对电力公司的信任。

4 结语

目前对居民用电客户的用电量预测工作尚处于探索阶段，较主网及大工业用电客户的电量预测还有很大的差距。本研究基于指数平滑算法中的累加形式的三次指数平滑算法实现了庆阳市居民用电量的短期(3 d)预测，其平均预测误差控制在4%以内，预测效果良好，为了进一步研究居民用电量，本研究在此基础上进行了居民用电气象敏感度分析，从而制定相应的策略，提前防范极端事件发生时对电力公司与居民客户带来的损失，但是本文提出的不可控因素之间存在多重共线性，可能在一定程度上会影响对居民用电量的判断，可以用，ridge，lasso等方法进行变量稀疏化，再进一步进行研究。