单种群两阶段竞争模型的能控性、能观测性及状态反馈分析

侯云艳，华志强，黄玉洁，程 研，陈丽莹

(内蒙古民族大学 数理学院，内蒙古 通辽028000)

棉铃虫是一种严重危害棉花生长的害虫，它导致棉花大量减产.近年来，棉铃虫在棉花作物上发生危害的趋势明显加重[1].棉铃虫广泛地分布于我国各地，是一种钻蛀性害虫，主要发生在棉花的蕾铃期.据相关数据统计，我国每年棉田因棉铃虫原因损害15%～20%，对我国农业发展有很大影响.棉花是民生中不可或缺的产品，是基本的民生需求.为了保证我国棉花的稳定生产，对生物种群以及生态环境进行定量分析并增加适当的生物控制，保证生态系统的平衡和生物种群的生存具有重要的理论意义和实际意义.卓义峰与慕嘉[2]通过对具有捕获率的一类捕食-食饵模型进行分析，讨论了系统的稳定性.高旭[3]讨论具有种间竞争的捕食-食饵模型，通过对模型进行定性分析得到了最适合的捕食者和食饵数量，从而使生态系统达到动态平衡.此外，国内外还有许多学者对不同模型进行定性分析[4-8]，得到使生物种群存在的必要条件，从而最终实现生态系统的动态平衡.

20世纪40年代，Volterra利用现代生态学理论通过微分方程建立了两种群竞争共生模型：

(1)

其中x和y为两种群在t时刻的种群密度.由于不同种群之间存在着相互作用、相互影响，种群x在成长的过程中不但会受到自身的作用，也会受到种群y对其的影响.设β11为种群x自身的密度制约，β22为种群y自身的密度制约；β12为种群y对种群x的影响，β21为种群x对种群y的影响.

近年来，生态问题日益突出，因此不断有学者将Volterra模型进行推广，对模型进行理论研究并赋予实际意义，通过对模型的定性分析，更清晰地描述了系统的动态行为.自20世纪70年代起，种群动力学理论研究迅速发展，阐述了一些生物现象，并给出了许多有效的生态数学理论.常见的种群动力学模型有：Lotka-Volterra模型、时滞模型、功能反应模型、反应扩散模型以及年龄结构模型[9-12].生物种群间的关系是生物数学理论重要的一部分，种群之间的主要关系是捕食与被捕食、竞争和共生.本文通过不同时期两阶段的竞争和共生关系建立生物数学模型，研究单种群不同时期两阶段的平衡关系、能控性和能观测性以及系统状态反馈的能控性.

1 建构生物模型及模型假设

在Volterra模型原理的基础上，考虑种群x划分为不同时期的2个阶段，种群x不同时期2个阶段存在竞争和共生的关系.现根据生物数学理论建立模型，并做如下假设：

1) 种群z在相对分布均匀的空间生存，空间上不涉及迁入和迁出的情况.

2) 种群z在生活空间上一直有较为稳定的资源供给，且种群z1、z2内部个体有均匀的机会获得资源供给.

3) 种群z在空间上的结构相对稳定，种群两阶段不同时期的增长速率相对一致.

4) 种群z自身的密度制约对个体的影响程度是均等的.

假设r1、r2为种群z的z1、z2阶段的死亡率，d1表示z1向z2转化的转化率，a11、a22为种群z的z1、z2阶段相互之间的影响，a12、a21为种群z的z1、z2阶段各自的密度制约.为了方便起见，令-b1为种群z的z1阶段的死亡率与z1向z2转化的转化率之和，-b2为种群z的z2阶段的死亡率，即-b1=r1+d1,-b2=r2.故基于Volterra模型建立一种群两阶段竞争共生模型如下：

(2)

由Volterra模型可知:①a11<0,a22<0，因为种群z的z1,z2阶段是竞争关系.②a12<0,a21<0，因为种群z的z1,z2阶段是密度制约.③ 0≤r1≤1,0≤r2≤1,0≤d1≤1.

2 模型分析

2.1 模型平衡点分析

定理1 如果a11b2-a21b1,a22b1-a12b2,a11a22-a12a21同号时，则系统存在唯一的正平衡点.

证明令

将微分方程组转化成：

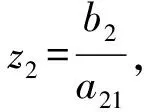
解得

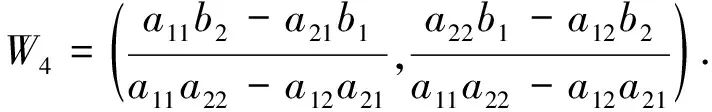
综上，系统存在4个平衡点：

2.2 平衡点稳定性分析

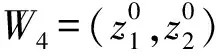
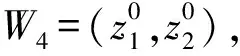
由稳定的Routh-Hurwitz条件p>0,q>0，其中p=-gs1-fs2,q=detJ.

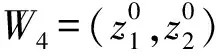
综上可知，系统中种群z两阶段z1(t)、z2(t)相互作用，可以达到种群z不同时期两阶段共存的稳定的平衡状态.

2.3 系统的能控性、能观测性

故系统可以写成：

(3)

现对系统增加控制，并给定输出：

(4)

(5)

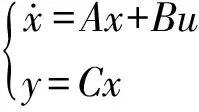
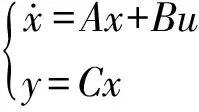
2.4 系统的能控性判定

接下来给出系统的能控性判定定理3和系统能观测性判定定理4.

定理3 如果系统(5)中a′+c′≠0或b′+d′≠0时，rank[BAB]=2，则系统是完全能控的.

证明

显然系统(5)的能观测矩阵rank(Uc)=2，由引理1知系统(5)是完全能控的.

定理4 如果系统(5)中a′+c′≠0或b′+d′≠0时，rank(U0)=2，则系统是完全能观测的.

证明

当系统(5)中a′+c′≠0或b′+d′≠0时，rank(U0)=2，由引理2知系统是完全能观测的.

2.5 系统经过状态反馈后的能控性分析

状态反馈是现代控制理论中特殊的一种控制方式，状态变量能够反映系统内部特征，从而对系统变量进行状态反馈，能更有效地改善系统的内部性能.状态反馈即将系统(5)的状态发出的信号作为系统的反馈量.现在系统(5)中引入反馈控制律：

其中v为2维控制输入向量，K为2×2状态反馈增益矩阵，L为2×2非奇异实常数矩阵.经过状态反馈的系统状态空间表达式为

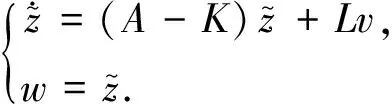
(6)

定理5 对于任何实常数矩阵K，当系统(5)中c′+d′≠0时，系统(6)也是完全能控的.

证明系统(5)的能控性矩阵为Uc=[EAEA2E].系统(6)的能控性矩阵为

综上可得，当系统(5)中c′+d′≠0时，系统(6)也是完全能控的.

3 数值模拟

为了研究在自然生物背景下，模型(2)与模型(5)的生物意义.通过收集实验数据，利用Matlab对模型(2)与模型(5)进行数值模拟.在系统的生物意义下，通过对单种群竞争模型(2)施加控制，将单种群竞争模型(2)转变为线性时不变系统(5)，从而最终实现生态系统的动态平衡.现对模型(2)、模型(5)取4组参数：

其中图1～4中的图(a)为模型(2)取4组参数时，模型(2)的z1、z2两阶段的种群数量随时间的变化关系.图1～4中的图(b)为通过对单种群竞争模型(2)施加控制，将单种群竞争模型(2)转变为线性时不变系统(5)，模型(5)的阶跃函数随时间变化的时间响应图.

通过对模型(2)和模型(5)取多组相同的参数，可以发现当棉铃虫z1阶段的死亡率加转化率大于棉铃虫z2阶段的死亡率时，模型(2)两条曲线无交点且逐渐趋于0，模型(5)经过对系统施加控制后逐渐趋于稳定但趋于稳定较慢；当棉铃虫z1阶段的死亡率加转化率小于棉铃虫z2阶段的死亡率时，模型(2)两条曲线有交点且逐渐趋于零，模型(5)经过对系统施加控制后逐渐趋于稳定且趋于稳定较快.图1～4均有较明显的生物意义，虽然趋于稳定的速度与程度不同，但最终都实现了系统的可控性.

(a) 种群数量图 (b) 时间响应图 (a) 种群数量图 (b) 时间响应图图1 模型(2)与模型(5)取第1组参数结果 图2 模型(2)与模型(5)取第2组参数结果

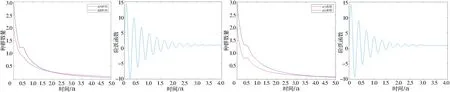
(a) 种群数量图 (b) 时间响应图 (a) 种群数量图 (b) 时间响应图图3 模型(2)与模型(5)取第3组参数结果 图4 模型(2)与模型(5)取第4组参数结果

4 结语

生态问题已经逐渐成为当前的焦点问题，本文根据Volterra模型以及生物学背景建立单种群竞争模型，通过对单种群不同时期两阶段进行分析，得出系统的稳定点及能控、能观测的条件.通过对系统施加控制，将种群模型转化为线性时不变系统，实现种群的能控性，从而可知，对种群施加控制来实现生态系统平衡有重要的作用.