土工袋抗土体静态液化机制探讨
2022-10-24沈超敏刘斯宏史丽雯
沈超敏 刘斯宏 史丽雯 邓 刚 严 俊
(1.河海大学 水利水电学院,南京 210024;2.中国建筑第二工程局有限公司,北京 100054;3.中国水利水电科学研究院,北京 100044)
砂土在饱和条件下的孔隙水压力增大会引起抗剪强度大幅降低甚至为零,这种现象统称为液化.土体的液化按其成因分类主要有两种:地震动力荷载下的循环液化和静态荷载引起的静态液化.1964年的日本Niigata地震和美国Alaska地震使循环荷载下的砂土液化受到了学术界的极大重视,而静态液化的概念直到20世纪90年代才开始逐渐引起各国学者注意.静态液化是指加载条件下的饱和松散砂土在无法及时排出孔隙水时突然出现的强度丧失现象.其实在20世纪初,Hazen[1]就已经使用“液化”的术语描述1918年Calaveras土坝的溃坝事件,之后陆续有文献报道了土体静态液化引起的流滑事故.尽管之后的20世纪60年代,Castro和Poulos[2-3]进行了大量的室内试验,很大程度上提高了人们对静态液化的认识,然而砂土的静态液化并未引起足够的重视.20世纪90年代,Morgenstern[4-6]列举了一系列在没有任何动力影响条件下的土体流动破坏现象,并将静态液化与常规土体破坏对比,发现静态液化往往发生在土体达到破坏强度之前.Yamamuro等[7]对比了临界状态理论与静态液化残余强度的关系,提出了稳定状态的概念.Lade[8]给出了砂土静态液化失稳线,并基于失稳线概念对较缓的水下边坡进行稳定性分析.吕玺琳等[9]基于二阶功理论,提出了根据弹塑性刚度矩阵的数学特性预判静态液化的触发.
土工袋是将软弱土体放入土工编制袋内,通过袋子加筋土体,从而提升土体结构性能的技术.研究表明,土工袋可以对袋内土体提供附加的约束力,从而提升袋内土体的力学性能.近年来,土工袋在一些重要的土木水利工程中得到了应用,如地基、边坡、挡墙缓冲层、尾矿处置等工程,并在防土体的静态液化失稳等方面呈现出了显著的优势.以采用模袋(长土工袋)加固的细粒尾矿砂为例(如图1所示),不经加固的尾矿坝属于典型的易发生静态液化失稳的工程,通过模袋的加固,极大提升了尾矿坝的稳定性.然而,由于土体的静态液化概念相对较新,土工袋如何通过袋土的相互作用改善土体的静态液化问题方面更是处于空白状态.本文尝试基于Hill失稳的准则,在土体的弹塑性本构理论框架内探讨土体静态液化的机理,在临界状态理论本构模型的框架内讨论静态液化满足的条件和其成因,从而进一步揭示土工袋在抗土体静态液化的机理.

图1 云南某尾矿模袋[10]
1 砂土液化的典型规律
大量的室内试验结果表明,松砂试样在不排水条件下的静三轴试验应力-应变曲线可以有4种典型的形式:暂时静态液化,完全静态液化,暂时失稳,完全失稳.静态液化和暂时液化中发生的体缩与颗粒结构在剪切过程中重组有关[11].
然而不管是哪种破坏形式,其触发模式都相同.典型的土体静态液化(失稳)的应力-应变关系如图2(a)所示,其剪应力q在达到峰值强度后迅速降低到稳定应力状态.此时稳定状态的应力状态对应的剪应力会在极短时间产生剧烈的降低甚至为零.这样低的残余剪应力使得土体出现类似流体的滑动现象,因此静态液化造成的破坏也被称为“流滑”破坏.以某饱和松散砂土试样的不排水剪切试验有效应力路径为例,饱和砂土的静态液化有效应力路径经历了图2(b)中的点A-C-D的过程.发生静态液化时,在(p,q)平面内的应力路径有着如下特征:①峰值剪切强度对应的应力比(点C)并未达到其临界状态线(稳定状态线上的点D),然而其应力比超过了屈服面顶点的应力比(点B);②发生静态液化以后,随着峰值强度的迅速降低,其应力比(q/p)还在持续增大(点C至点D);③最终的稳定状态(点D)对应的抗剪强度可能高于或者低于其峰值强度(与暂态液化或者失稳有关),然而其应力比(p/q)却与排水条件达到的临界状态应力比相同.

图2 典型的饱和砂土液化/失稳触发模式
失稳理论是通过二阶功反映材料稳定性的通用准则,目前大多数研究结果表明,静态液化的触发机制可以用失稳理论阐述.为此,本文尝试在失稳理论的框架内探讨该问题.
2 弹塑性本构框架下的液化阐述
2.1 土体弹塑性本构框架
本文在土体弹塑性本构理论框架内讨论土工袋的液化失稳问题.为了不失一般性,讨论中不涉及具体的本构模型,而是采用土体弹塑性本构经典的理论框架.本文讨论仅限于(p,q)空间内,即忽略中主应力对本构模型的影响.文中涉及的应力如不加说明,均为有效应力.
土体的屈服面可以写作如下形式:
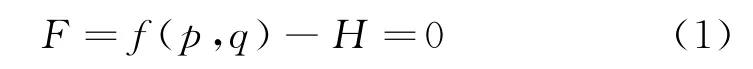
式中:H为硬化参数,其通用的形式为[12]:
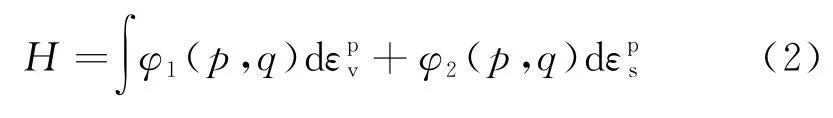

当应力状态到达屈服面时,发生塑性变形,塑性应变增量和应力增量满足如下关系:

式中:g为塑性势面.屈服发生后,如果不卸载,则应力始终在屈服面上,因此有dF=0,即:

记土体的剪胀方程的一般形式为[13]:

式中:D为剪胀比;η为应力比;ψ为状态参量;C为材料参数;Q为内变量.
将式(5)代入式(4)可得:
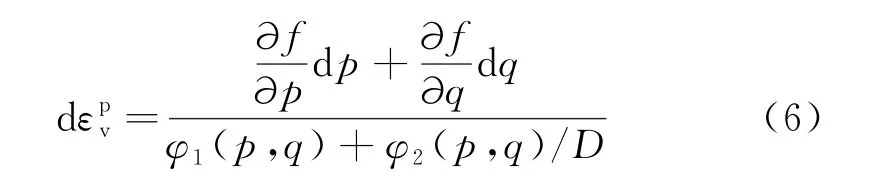
结合剪胀方程同样可以求出偏应变增量.

2.2 基于Hill失稳的土工袋静态液化条件
土体的静态液化可以归结为分散性失稳的一种,本文基于Hill[14]的二阶功原理来判别土体稳定,即在小变形条件下,若要使材料稳定,需满足:

将式(8)代入式(7)可得:
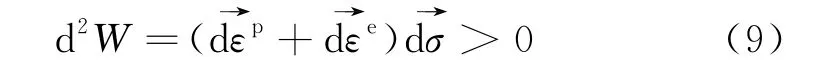
这里弹性应变部分由于砂土作为一种无黏性土,故可认为其剪切变形近似不可恢复,即有
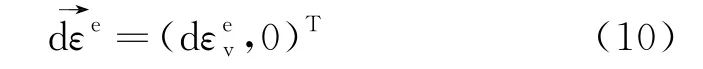
将式(9)(10)代入式(7)可得
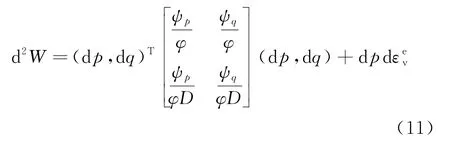
整理后有


其中:κ为体变的弹性回弹模量,v=1+e.将式(13)代入式(12)整理可得
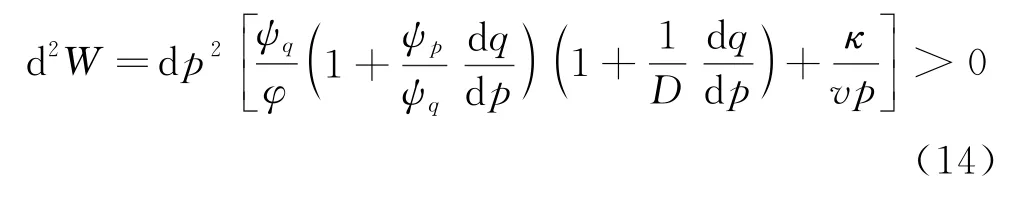
上式给出了在应力空间内任意加载路径下的二阶功的表达式,注意到式中ψq和κ/vp在加载过程中恒为正,因此当砂土发生静态液化时,要使得二阶功从正变为负,必然伴随着ψp/ψq,dq/dp或D 正负的变化,也就是说在液化前(或液化时)屈服面方向、塑性势面方向和应力增量方向中至少有一个改变其所处的象限.同时,注意到κ/vp这个恒正项与孔隙比成反比,因此减小孔隙比可以提高二阶功的值,从而避免土体发生液化失稳.
3 土的失稳与土工袋抗液化机制
3.1 土体的失稳路径
针对不同的剪切路径分别分析其发生失稳的可能性和对应的应力关系.
1)等向压缩路径
在等向压缩过程中,没有剪应力q,因此二阶功可以退化为如下形式:
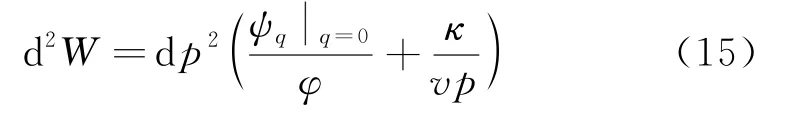
根据ψq,φ以及p的非负性易知d2W>0 恒成立,也就是说等向压缩过程不会发生液化或失稳,这也与对土体的认知常识和室内试验结果吻合.
2)等p剪切路径
此处讨论的p是有效应力,在排水条件下保证有效球应力为定值的剪切,因此剪切过程中始终满足dp=0.由于式(14)中dp分别出现在分子分母上,稍作整理后将dp=0代入式(14)可知:
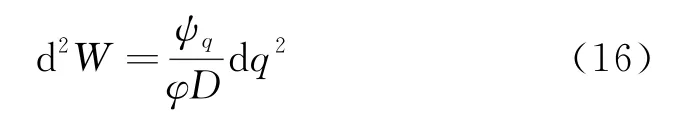
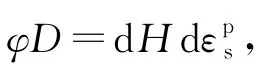
排水条件下的等p剪切对应的失稳与静态液化是有较大区别的,主要表现为此时体应变表现并不一定是剪缩,事实上,大部分试验结果表明[15],在等p剪切阶段发生失稳发生在剪胀阶段,且对应的是应力比的小幅度软化.
3)饱和不排水剪切路径
饱和砂土不排水剪切路径对应着总体积变形为零的假设,即

将式(17)代入式(14)易得
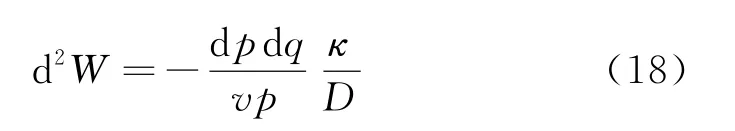
从上式可以看出,在不排水条件下剪切时,其二阶功与应力增量的方向和剪胀的方向有关.图2(b)中不排水剪切条件下应力在有效应力路径的最高点dqdp的符号发生改变:在加载初期,dq>0,dp<0,松砂发生剪缩,D>0,因此对应d2W>0.当应力增大到一定程度,出现dq<0,dp<0时,此时对应的二阶功符号同样发生变化,d2W=0初值不稳定点)的应力满足

即为有效应力路径的最高点.值得注意的是,等p剪切的软化对应的是屈服面的收缩,而砂土在不排水条件下的液化对应的屈服面可以仍处于扩张阶段(dH>0).
下面针对完全液化和暂时液化展开讨论:
式(13)的弹性体应变与球应力p的关系在不排水条件下依然成立,结合式(17)可知

由于剪应变恒为正,因此我们可以得到如下结论:在不排水条件下,剪缩时有效应力dp<0,剪胀时dp>0.换句话说,剪缩时,孔隙水压力增大,有效应力降低,反之剪胀过程中孔隙水压力减小,有效应力增大.
若某一排水剪切试验中发生暂时静态液化现象,也就是说在应力衰退一段时间后出现应力回升,dq>0,dp>0,则此时根据式(20)的推论可知,此时土体剪胀,D<0,根据式(20)的判别条件可知此时土体恢复稳定状态(如图3(b)所示).反之,若土体发生的是完全液化,则此时并无剪胀出现(如图3(a)所示).以上的讨论表明土体的液化触发条件d2W=0,然而其剪胀特性决定了液化是完全的还是暂时的.对于更加密实的试样,有可能在未出现dq=0 之前就发生剪胀,则此时应力路径与图3(c)相同.
3.2 土工袋抗液化机制
土工袋对袋内土体提供约束作用,从而提升土工袋整体的抗液化稳定性.以二维情况下的土工袋约束作用为例,目前对其约束机制有两类解释,分别是等周假设和等张力假设.下面针对两种假设分别讨论.
土工袋的等周假设基本概念是将土工袋作为一个刚性的约束“箍”住袋内土体,袋体的周长不发生变化,即

式中:H和B分别为袋子的高和长.进一步式(21)可以写作应变的形式

式中:εH和εB分别为土工袋沿宽度和长度方向的应变,且约定压缩为正.若土体为饱和不排水条件,显然仍需要满足总体积变形为零的假设,即

结合式(22)和式(23)可发现方程有唯一的解,即εH=εB=0,表明土工袋处于完全约束状态,不会产生液化变形.这一结果也符合直观理解:完全不可变形的袋内部即使土体完全没有强度,只要袋子不破坏,作为整体也不会发生失稳破坏.
由于第一种等周假设过于理想化,进一步采用土工袋的等张力假设分析.Matsuoka和Liu[16]分析了袋内土体的平衡方程,对于横截面为图5所示的土工袋,忽略其形状的不规则性以及边角的弧度,近似认为土工袋为长方形,其宽与高分别为B和H.假定土工袋在二维情况下的张力T沿着袋周是均匀分布的,则土工袋袋子侧向和竖向的平衡方程分别为
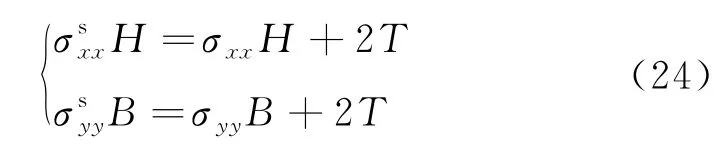


图4 土工袋与袋内土体应力关系
对于处于弹性阶段的袋子,其张力与沿着袋周方向的应变εl成正比,写作

式中:E l为袋体单宽模量;εl压为正,根据其定义可以写作

Shen等[17]借鉴了土体有效应力原理,提出了土工袋强度变形特性的方程

式中:σ和σa分别为土工袋受到的外应力和袋子对袋内土体的附加应力;K为袋内土体的劲度张量.因此,土工袋的二阶功写作
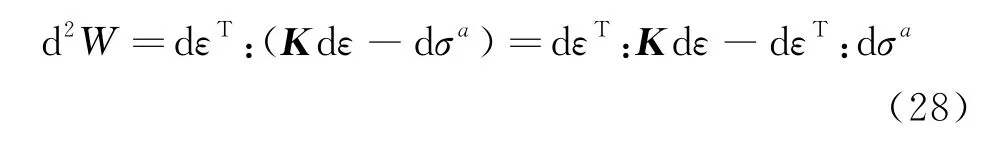
式中:dεT:Kdε项为袋内土体的二阶功,其值主要取决于袋内土体的材料特性;-dεT:dσa为袋子引起的附加二阶功.土工袋是否能够提升土体的抗液化效果的问题可以归结为-dεT:dσa是否为正值.
结合式(21)中袋体附加应力分量的定义,袋体引起的附加二阶功部分为

上式结合式(25)和(26)可得
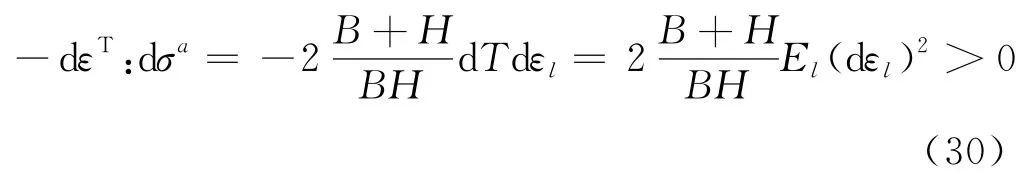
从式(30)可以发现:①由于式(30)恒为正,表明土工袋在任意应力路径下对土体的抗静态液化稳定性均有增益效果;②土工袋模量E l的增加可以提升土工袋的抗液化稳定性;③袋体截面的比周长,即单位表面积的周长(B+H)/BH的增加有助于提升土工袋的稳定性,此结论的推论也表明,同样的长宽比和袋体材料条件下,土工袋越小,抗液化稳定性越好.
4 结论
本文基于Hill二阶功失稳研究了土工袋的静态液化机制问题.为此,首先在弹塑性本构理论框架内讨论了土体静态液化的模式与土体屈服、硬化以及剪胀性的关系.并分别在等周和等张力假设条件下,探讨了土工袋的抗静态液化的机制.主要结论如下:
1)土体的静态液化触发条件可以通过Hill二阶功失稳判据识别,但液化后为暂态液化或完全液化与土体的剪胀特性有关.若土体呈剪缩性,则发生的是完全液化,若土体呈剪胀性,则液化为暂时液化.
2)从土工袋的应变约束作用看,土工袋通过限制土体的允许应变路径,约束了袋内土体静态液化的发展;从Hill二阶功准则看,土工袋对袋内土体提供的附加二阶功恒为正,有助于降低土体的静态液化风险.
3)土工袋袋体模量增加可以提升土工袋的抗液化稳定性;袋体截面的比周长,即单位表面积的周长(B+H)/BH的增加有助于提升土工袋的稳定性.换言之,同样的长宽比和袋体材料条件下,土工袋越小,抗液化稳定性越好.
