问题导向引领下的数学探究式教学——以“圆的标准方程”教学为例

盛 茜

(江苏省常州市田家炳高级中学,213000)

苏教版高中实验教材《数学》必修二第二章2.2.1“圆的方程”第一课时“圆的标准方程”是在学习了直线的方程之后首先遇到的曲线方程． 作为新授课,其目的就是为了让学生在问题情境中明白数学的实用性,在问题串的引领下用所学数学知识解决实际问题．教学时可采用“问题情境——学生活动——建构数学——数学运用——回顾反思”的方式来设计教学,巧妙设计“问题情境”和“问题串”，常可收到好的效果．

一、“问题情境”的设计

“问题情境”如下:已知隧道的截面是半径为4 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?

反思问题情境设计的目的在于唤醒学生的注意,从情境中发现并抽象出数学问题,进而能够为了解决问题而进行积极的数学活动．这个问题情境来源于实际生活,也是教材的一道例题.在这个实际问题情境下,学生的兴趣被激发出来，注意力一下子被集中起来.从心理学角度来说,学生自然地产生主动学习的“心向”．因此,问题情境设计的核心原则是:有利于学生思维品质的改善,有利于学生探究能力的发展,有利于学生创新意识的培养,充分关注学生数学核心素养的养成过程． 因此，在创设实际问题情境时，应注意问题情境的依托性(适度性)、导向性、探究性．

1.依托性

问题情境来源于真实的生活，但必须包含明确的数学问题,最重要的是符合学生的认知特点．车过隧道问题是学生在生活中常见的问题,而且与本节课的知识密切相关．因此具备了较好的依托性原则,这样的情境设计有利于学生展开思维活动,从而能有效促使学生进行观察、归纳、概括、抽象、推理、论证等.在实际教学过程中,绝大部分学生都能根据自己的生活实际，较好地理解情境,为进一步学习探究奠定基础．

2.导向性

所谓导向性原则是指在设计问题情境时必须要突出“问题”这个核心,能引导学生提出相应的数学问题．在实际情境中伴随着观察、猜想、抽象等思维活动的展开,逐步将问题集中抽象到建立“圆的方程”这个主题上来,因此这个情境就具有较好的导向性．在课堂教学中,学生对于问题的导向能作出相应的回应,顺利地进入到各个环节的探究中去． 问题是数学的心脏,问题是思维的核心,没有问题,思维便无法启动．

3.探究性

问题情境的特点具有开放性、新颖性、对学生的思维有一定的挑战性．因此，设计问题情境时，应当充分激发学生的探究欲望．在实际问题情境中,解决的方法多种多样,可以用初中平面几何知识解决问题,也可以用三角函数知识解决问题等等.对于学生来说,可以很好地拓展思维空间,激发对新知识探究的渴望,同时也为引出本节课的主题作好铺垫．

二、“问题串”的设计

问题1你有怎样的方法解决上述问题?

问题2考虑解析几何方法时,以半圆的圆心为坐标原点,直径所在直线为x轴．这样货车的宽和高分别对应什么(顶点的横坐标与纵坐标，图2)?

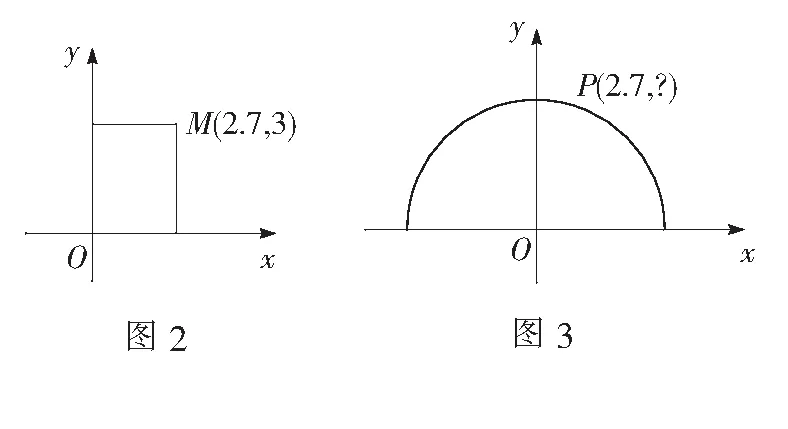
问题3需要求出哪个量就可以作出判断(如图3)?

问题4初中圆的定义是什么?请画出圆,并用符号语言表示(如图4)．

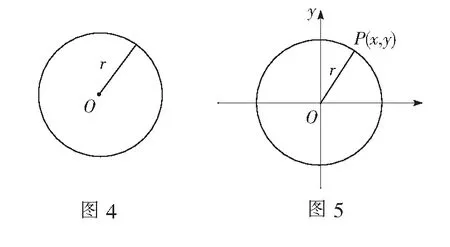
问题5引入平面直角坐标系后,请将上述符号语言转化为代数方程表示(如图5).

问题6尝试总结推导圆的方程的步骤．

问题7用解析几何方法解决情境中的问题．

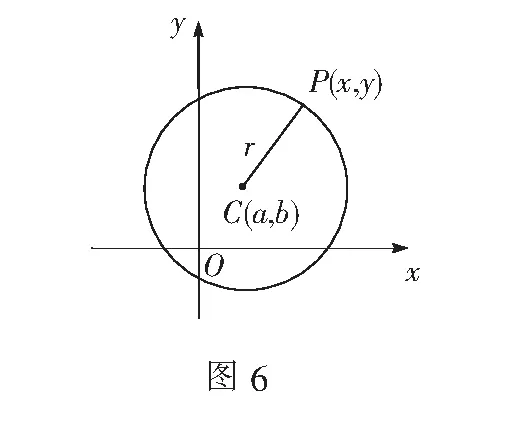
问题8在平面直角坐标系下,以C(a,b)为圆心,r为半径的圆的方程是什么(图6)?

问题9求圆的标准方程需要几个独立的条件?

问题10请思考情境中的问题还有怎样的解决方法?

问题11在解析几何问题中,一方面需要将“形”的问题转化为“数”的问题来研究,另一方面还有什么呢?

反思每个数学教师都知道,问题是数学学习的根基，有效的问题情境设计,才能打开学生的思维“匣子”,从而进行有效的数学思维活动．本节课用11个环环相扣的问题串成一条主线，贯穿整个课堂．通常在进行问题串的设计时应遵循整体性、层次性、探究性的原则．

1.整体性

本节课从问题情境的第一个问题出发,逐步引导学生围绕本节课的知识结构与思维方式展开.在设计上环环相扣,逐步追问,并且在第一次解决问题后并没有就此结束,而是引导学生向思维的更深处发展,最终回归到解析几何本质问题的理解，较好地呈现了思维脉络的整体一贯性．

2.层次性

本节课的11个问题的设计，首先从问题1的开放性问题开始,让每个学生都“有话可说”,符合新课程理念,兼顾各个不同学习能力层次的学生.其次从问题2开始到问题6引导学生从数的角度解释问题,开始用数学的思维思考问题,分析问题.然后从问题7开始到问题9,用数的方式解决实际的几何问题.最终的问题10、问题11的目的在于引导学生将实际问题最终抽象成解析几何的本质问题,达到数学抽象的目的．这样的设计层次分明,有利于学生思维的不断加深,引导学生对数学本质进行探究．在经历解决问题整个过程的同时，学生学会了提出问题、分析问题、解决问题的一般方法．

3.探究性

培养学生的自主探究能力是实施新课程的目的所在．“问题”设计的好坏，决定着能否引导学生真正进行有效的数学探究．本节课,从实际问题出发,逐步设问,引导学生探究建立“圆的方程”的必要性,进而激发学生进一步思考建立方程的方法与步骤,然后用新建立的方程来解决问题,有效地促进了学生理解并掌握圆方程建立过程．这11个问题实际上是不断进行探究,不断在已有认识基础上推进,探究的内容越来越深入．

在数学教学中,教师的“教”和学生的“学”应该自然地融入到“问题”中去．教师通过设计问题、提出问题来促使学生对问题进行思考,而不是干巴巴地讲解知识.学生通过对问题的思考促进思维活动的形成,从而掌握思考问题的方法,获得能力的提升．应相信学生在不断地解决各个问题的过程中能体验学习数学的乐趣,增长数学知识,最终形成解决问题的能力,为进一步发展奠定基础．因此,数学教学就是提出问题与解决问题的教学,在问题的设计中提升教师的教学能力,在问题的解决中发展学生的思维能力．

综上可知，在问题设计中,要对学生数学基础、考试要求作出充分考虑,找到其中的平衡点.只有围绕这一平衡点来进行数学探究式课堂的构建，才能够保障教学有效性,在提升学生数学成绩的同时,锻炼其学习能力,同时促进教师自身的专业成长．