数形结合:让学生解决实际问题能力真实落地
2022-10-24于晓兰江苏省无锡市东北塘实验小学
于晓兰(江苏省无锡市东北塘实验小学)
数形结合数学思想能够将抽象的数学语言转化为直观图形便于学生理解,将数形结合用于小学数学教学中有利于帮助学生掌握数学问题的本质,对提高学生解决实际问题的能力具有重要的意义。
一、数形结合发展数感
数感主要是指个人对数字理解与运用的能力,良好的数感对于学生数学学习以及理科思维的培养有着重要的意义。尤其是在小学数与代数问题的分析与解答中,学生如果具有良好的数感,可以更好地明确数学题干中数量关系,可以帮助学生用数学思维更好更快地解决实际生活中的数学问题。
例如,在《认识多位数》一课教学中,让学生复习之前学习过的万以内数的知识。在此基础上,学生拿出课前准备好的计数器,让学生在计数器上拨出1000,再每次增加1000,直至拨至9000,再让学生思考:“如果9000+1000是多少,在计数器上如何拨出这一数字?”让学生结合问题在计数器上拨出10000,再每次增加10000,直至拨至90000,再提出问题:“如果90000+10000是多少,在计数器上如何拨出这一数字?”让学生通过波动计数器数字认识的10个1万是10万,万位满10应该怎样处理。再让学生结合计数器播出数字的变化以及教材中的例题进行写数与读数,初步认识数位与数位分级。在这一过程中,通过计数器上珠子的变化表示数的大小,让学生通过直观的珠子变化掌握十进制计数法。等到学生拨到9000数字后就会觉得计数器上的数位不够,有些学生就会想到使用新的计数器表示新的数位,但教师如果继续要求使用原有的计数器表示数位时,学生就会认识到直接进位是不可以的,需要将数位改写成万位再进一产生新的数位,再按照同样的方式数至9万时会自然产生新的数位——十万。学生在将计数器上珠子转化为新的数位过程中,实际上就是数形结合的过程,利用数形结合能够有效培养学生对万以上数字的数感。为了进一步培养学生的数感以及解决实际问题的能力,教师可以设计以下练习题:“一枚一元硬币的重量约为6克,那么1亿枚硬币的重量大概有多少?如果用载重10吨的汽车运输这些硬币,需要多少辆汽车才能一次性运输完毕?”配合多媒体课件的线段图等让学生结合所学知识去分析与解决现实生活中的问题,培养学生的数感与思维表象,用数形结合的方式也有利于提升学生解决实际问题的能力。
二、数形结合明确数量关系
教师在利用数形结合思想提高学生解决实际问题能力的过程中需要利用数形结合思想引导学生去剖析数量关系,这是学生顺利分析与解答数学问题的基础。例如,在解答“有一天,丁同学对甲、乙、丙三人的年龄进行了比较,发现甲的年龄是乙的两倍还比乙大三岁,而乙的年龄是丙的两倍且比丙小两岁,这三个人的年龄相加为109岁,那么甲、乙、丙三人的年龄分别是多少?”这一问题时,许多学生会感到这道题的题干叙述绕口、复杂,许多基础一般以及学困生在看到题干后毫无头绪。这时,教师就可以引导学生画出线段图(见图1),引导学生借助线段图去明确题干中的数量关系。

图1 甲、乙、丙年龄线段图
从图1中可以看出将丙的年龄设为1份,则乙的年龄少2份但需加2,甲的年龄减去3后是4份少2×2,所以这三人的年龄都是准备数时的和为:109+2-3+2×2=112岁,从线段图中可以得知三个人年龄的总分数为7份数,所以丙的年龄(1份数)为112÷7=16(岁),甲、乙二人的年龄分别为30岁与63岁。在解答知道生活中常出现的年龄问题时,将线段图应用于数学题目的分析与解答中,数与形的结合充分展示了题干中甲、乙、丙三人年龄这一数量之间的关系,将抽象的文字具象化地呈现出来,有助于发展学生的形象思维与抽象思维,可以通过直观的线段图帮助学生明确题干中的数量关系,为后续的解题打下了基础。
三、数形结合把握问题实质
教师在教学过程中应该注重利用数形结合思想去引导学生把握各类数学问题的实质。例如,在分析与解答面积问题时,学生很容易被题干中的文字叙述影响,无法了解题干中要求求的是哪一部分的图形面积,大多数学生也无法凭借着线段图去解决这类数学问题。这时教师就可以引导学生应用较为简单的示意图去让学生对面积问题进行本质理解与整体的判断,帮助学生明确题干中所求图形的面积范围等内容,帮助学生进一步明确题干中的已知信息,帮助学生更好地从已知过渡到未知。如在“小丁同学家中有一个长方形的菜园,长为25米,宽为10米,小丁的爷爷想要在菜园四周建一条宽两米的道路,则道路的面积是多少?”结合题干中信息,可以画出图2示意图,帮助学生明确题干所求部分图形的面积。
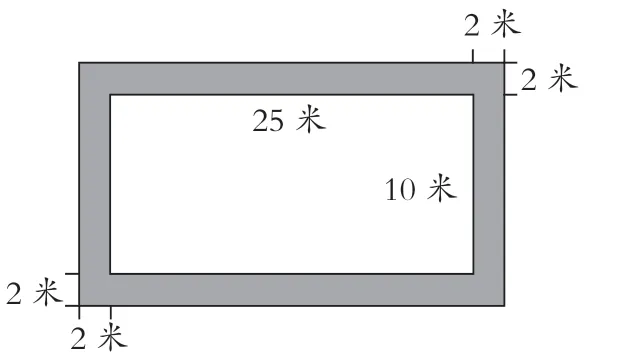
图2 菜园道路面积示意图
小学生很难把握题目中各变量之间的关系,尤其是面对较为复杂且计算量较大的数据时,一些学生使用逐个展开计算的方式很容易造成解题效率低下,也很有可能使学生因此产生厌学的心理。因此教师应该利用数形结合的思想帮助学生把握统计问题的实质,例如应用统计表格、点线图、柳卡图等简单的图形或示意图促进学生形象思维与抽象思维协调发展,帮助学生掌握解题方法与基本思路。
四、加强学生作图能力的训练
教师引导学生利用数形结合思想去解决实际问题,很大程度上需要学生自己作图去明确题干中的数量关系等已知条件,所以教师也应该注重对学生作图能力的训练与培养。首先教师在教学活动中应该尽可能地向学生介绍三角板等作图工具以及不同示意图的作用,让学生在作图过程中,明白不同示意图的绘制作用,以及能够结合题干内容以及解题的需要合理的选择示意图去辅助分析问题。教学过程中,教师需要为学生进行作图示范,在示范后向学生讲解做线段图、点线图等不同示意图的技巧,再让学生尝试独立作图,教师进行适当点拨,从而提高学生作图的规范性。在将数形结合思想方法用于小学数学教学中时,学生在作图解答数学问题的过程中,教师应该留给学生足够的作图与思考的时间,让学生独立作图与思考,再让学生进行合作交流,最后由教师进行总结与指导。这样,不断提高学生的作图能力,使学生在分析与解决问题的过程中能够更好地应用数形结合思想方法。
