“数”于其外，“函”形于内

董秀明（江苏省南京市科利华中学）

近年来，中考数学复习中，函数、方程、不等式融为一体、有机结合，成为一个热点专题。下面，笔者从“数于其外、函形于内”的视角浅谈该专题复习教学的组织与实施。

一、课前思考

设计意图：引导和帮助学生理清函数、方程、不等式的三者关系，挖掘深层内涵，构建知识“三角图”，渗透“数形结合”思想，提升学生思维能力。

教学目标：通过学习，学生能够理解函数、方程、不等式之间的关系；通过学习，学生能够综合函数、方程、不等式之间的关系解决问题；通过学习，学生能够进一步综合数学知识，感悟数学思想，提高解题能力。

教学重点：理解函数、方程、不等式之间的关系并能够综合三者关系解决问题。

教学难点：综合函数、方程、不等式之间的关系解决问题。

二、教学过程

（一）创设情境，提出课题

分析：前期试讲中，笔者曾尝试让学生直接说出函数、方程、不等式的联系，但效果不好。因此，笔者调整思路、创设情境，引导和帮助学生学习从归纳中理清三者关系。

（二）问题串联，以“形”研“数”

此方程是一个高次方程，初中生没有学过。这个问题的提出，对学生产生了巨大的冲击，“逼”着学生充分发挥函数和方程的联系，以“形”研“数”。

课堂上，笔者给予学生充足的时间思考，这是第一个问题，也是引领学生更有信心地往下走的一个开端。留有充足的时间，学生的思考会更充分，信心会更强。充分思考之后，学生给出此题的一个较为完整的解决思路。如下。

解：∵x≠0

(6)雾化方面:护理人员应每日给予患儿雾化辅助治疗,在雾化液中加入消炎药物,每次雾化保持在15min左右,一日5次。

由函数与方程的关系，此方程的根即为函数y=x2+2和的交点的横坐标。

分析：此题巧妙地以“形”研“数”，思路简单易操作，结论一目了然，学生尝到了以“形”研“数”的甜头。

此不等式组中的两个不等式，不等式①学生非常熟悉，易得解集为x＜1。

而对于不等式②，笔者发现学生出现了以下两种思路。

思路一（“数”的角度）：

由②，得2＜x，即x＞2.

综合①②得不等式组无解。

由②，得当x＞0时，得 2＜x，即x＞2；当x＜0时，得 2＞x，即x＜0。

∴x＞2或x＜0。

综合①②得不等式组解集为x＜0。

思路二（“形”的角度）：

令y＜1得解集x＞2或x＜0，从而综合①、②得不等式组解集为x＜0。

分析：两种不同的思路，一个从“数”的角度，一个从“形”的角度。笔者发现，思路一（“数”的角度）的解法中，大部分学生都出现了“错误解法”，究其原因是x的正负不确定，不等式基本性质的应用出现了错误。而“正确解法”虽然正确，但是相对于思路二（“形”的角度）来说，明显复杂，所以，我们发现此题若以“形”研“数”，则方法易且正确率高。

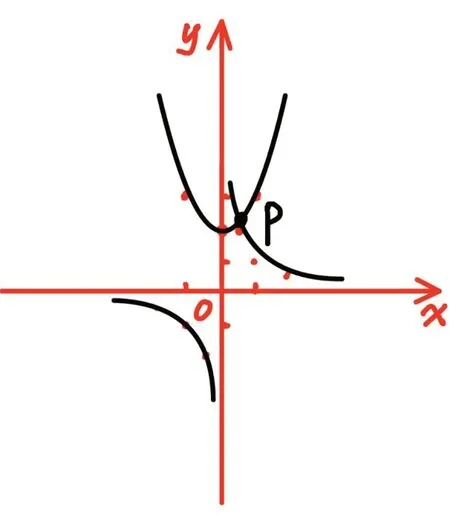
草图1

（三）画龙点睛，意味深长

本课至此，学生已经充分感受到，遇到“数”的问题，不仅能以“数”解“数”，更可以综合“数形结合”的数学思想方法，以“形”研“数”，使得方法简单、思路巧妙。

本课最后留给学生一道课后思考题，既与之前的情境呼应，又能充分体现本节课的主旨思想，可谓“画龙点睛，意味深长”。

三、教学反思

从本课的“设计意图”到“备课”“备学生”，再到“课堂全过程”，笔者分别在不同的班级分别授课，感受颇深。

（一）理解教材，强调课堂的自然生成

在研究教材、研究专题的基础上，笔者静心思考教材所体现的设计意图和设计思路，在专题部分多次调整问题，并将若干问题“串联”，层层深入，注重问题前后的联系和思想方法的渗透，注重课堂上学生的自然生成，努力体现以“形”研“数”“数形结合”的数学思想方法。

（二）理解学生，注重学生的合作探究

作为学生学习、课堂教学的“引导者”，带领学生一步步往前走，不仅需要教师在授课前充分地准备，更要学会在课堂上大胆地放手，充分地发挥学生相互之间的合作探究。特别是生生、师生之间的合作探究，尤为重要。

只有充分理解学生，相信学生，重视生生、师生之间的合作探究，课堂才能真正成为师生共成长、共进步的课堂。

（三）理解教学，体现深厚的思想内涵

数学课堂教学，教师不仅仅是把某个知识传授给学生，除了“传道授业”，更需要的是“解惑”。而如何“解惑”并教会学生“自主探究、自主解惑”，是所有数学教师面临的挑战。

课堂上，某一个数学知识的呈现，某一个数学方法的讲授，某一个数学思想的渗透，都需要我们教师充分地理解教学，把握数学，唯有这样，才能体现数学课堂深厚的思想内涵。