岩巷掘进中电子雷管爆破振动信号的时频能量分析

2022-10-24殷浩杰佟晓勇

金属矿山 2022年9期

孟彪殷浩杰陈辉,4 佟晓勇

(1.新疆雪峰科技(集团)股份有限公司,新疆乌鲁木齐 830000;2.新疆雪峰爆破工程有限公司,新疆乌鲁木齐 830000;3.新疆大学地质与矿业工程学院,新疆乌鲁木齐 830000;4.中南大学资源与安全工程学院湖南长沙 410083;5.新疆地质工程有限公司,新疆乌鲁木齐 830000)

伴随着我国工程建设领域相关技术的快速发展,工程爆破在隧道建设、矿山开采、城市拆除中的应用日益增多,与此同时爆破引起的安全隐患问题也频频出现,根据现场情况以及被保护对象的不同,其破坏机理与所采取的控制措施往往有较大区别[1-5]。对此,广大学者开展了大量研究,赵柯等[6]基于量纲理论,以埋地燃气管道为例,分析了影响其振动速度的物理量,并推导出了能够反映管道尺寸效应的振动速度预测公式。朱斌等[7]以隧道支护中的砂浆锚杆作为研究对象,利用ANSYS/LS-DYNA数值模拟软件,对不同围岩级别和支护条件下砂浆锚杆的动力响应特征进行了研究,研究结果对于指导现场支护工作具有重要意义。杨茂森等[8]以露天煤矿超高台阶为研究对象,探究了其爆破振动主频和持续时间的特点,并对台阶周围建(构)筑物进行了振动安全评估,极大保证了现场施工安全。吕虎波等[9]以下穿高速公路输水隧洞为研究对象,采用数值模拟结合现场试验的方法,研究了上覆高速公路路面振动响应特征及衰减规律。总体上,现有研究倾向于露天矿山、地下矿山或铁路、公路隧道等案例,被保护对象根据现场情况多有不同,对于挂帮矿这种露天转地下的特殊开采形式,对其振动规律的研究有待深入。挂帮矿露天开采部分的进行已经对边坡造成严重扰动,进而通过平硐转入山体内进行空场开采,伴随着山体内爆破活动的进行,必然会对薄弱的边坡及巷道造成严重损害,使其存在诸多安全隐患。因此研究挂帮矿的边坡及巷道在爆破振动下的动力响应特征,对于确保现场施工安全具有重要意义。

对于爆破振动信号,国内外研究人员在振动波的传播衰减规律[10]、振动波的时频能量分布特征[11-13]、减振方法和振动波的损伤机理[14-17]等方面展开了深入研究。主要研究方法为:运用ANSYS/LS-DYNA等数值模拟软件建立相似模型、运用萨道夫斯基公式和线性回归方程建立振动速度衰减模型、运用小波理论和傅里叶变换进行振动信号的频谱分析等。其中在振动信号的频谱分析中,应用较为广泛的为傅里叶变换法和小波分析法,但这两种方法仍存在着不同的局限性,傅里叶变换法不能在实质上分析非线性非平稳信号,小波分析法在小波基底的选择上受主观因素影响很大。而HHT作为一种新兴的信号分析方法,具有高度的自适应性,能够有效克服上述不足,并且能够更加直观地反映振动波在时间—频率—能量上的分布特性。本研究运用HHT法对备战铁矿岩巷掘进时的实测爆破振动信号进行分析,将振动波传播过程中的时间、频率和能量三要素相结合,分析电子雷管应用于工程爆破中的特点,对电子雷管的推广使用、爆破参数优化、减小振动危害、明确振动波的传播机理等具有重要意义。

1 Hilbert-Huang变换法理论分析

1.1 EMD分解

HUANG等[18]认为,振动发生后,存在着一些具有非正弦函数特征的IMF分量,他们共同组成了包括冲击信号在内的任何复杂信号,并且这些IMF分量通常较为简单。通过EMD分解可实现对这些IMF分量的提取,其中EMD分解以最终分解得到的残余分量作为结束标志,其算法表达式为

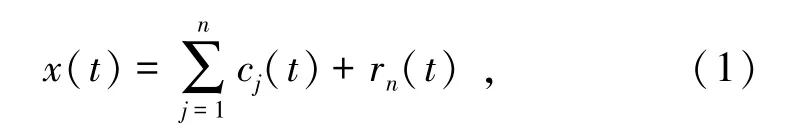
式中,c1(t)、c2(t)、c3(t),…,cn(t)依次表示原始信号在不同频段的成分,共同组成了原始振动信号,且他们的频率呈下降趋势,这些小频段的频带范围并不是固定的,证明了EMD分解具有自适应的特性;rn(t)为计算最终得到的余量;n为算式最终循环筛选次数。

1.2 Hilbert变换

对分解得到的各IMF分量进行Hilbert变换,得到各分量对应的瞬时频率,对所有的瞬时频谱进行综合后可得Hilbert谱[19]。计算步骤如下:

对所有分量进行Hilbert变换,公式为

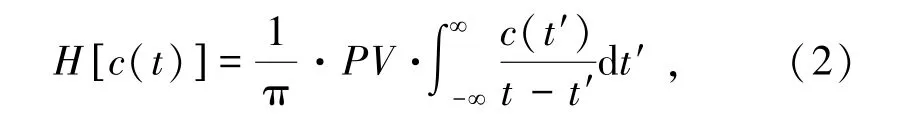
该公式表示将函数c(t')与1/(πt)做卷积运算,式中,c(t')表示某一实值函数;t'为实值函数变量;PV为柯西主值,对此构造解析信号z(t):

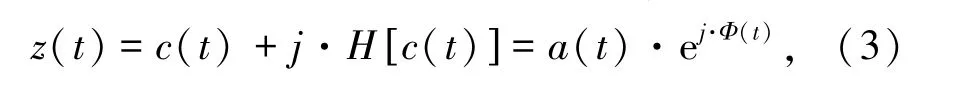
式中,j为解析常数;a(t)为幅值函数;Φ(t)为相位函数,公式分别为

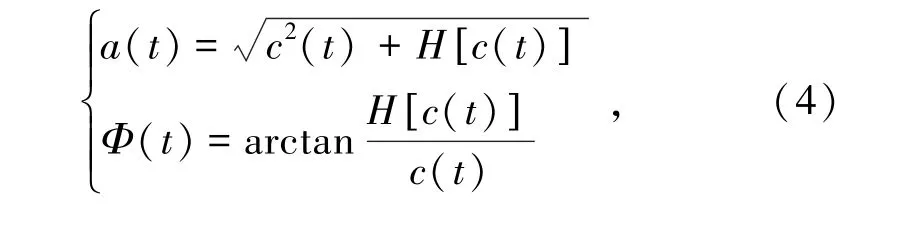
式中,c(t)为信号x(t)的IMF分量。

2 爆破施工方案与爆破参数

2.1 矿山概况

备战铁矿矿区位于和静县城327°方向160 km处,与和静县巴仑台镇路距130 km,直线距离84 km。该矿露天开采部分已经完成,现转为挂帮开采,且挂帮开采部分已由空场法转变为无底柱分段崩落法。2019年8月,3 476 m中段中已回采结束的采场中,预留的间柱和顶柱发生垮塌,出现顶板(3 536 m水平)与露天边坡垮塌贯通,并导致3 572 m露天边坡发生局部垮塌。矿柱及边坡的不稳定因素大大增加了爆破施工的难度。因此开展对爆破振动传播规律的研究,有效控制爆破振动,对于矿山安全生产具有重要意义。

2.2 爆破方案与爆破参数

测试期间工作面采用双楔形掏槽,第1圈掏槽眼平均孔深1.14 m,第2圈掏槽眼平均孔深2.07 m,辅助眼、周边眼孔深均为2.2～2.3 m,炮孔直径均为40 mm。

自2021年9月27日起,在该矿山进行了多次测振工作,本次分析选用9月28日某一出矿进路运用电子雷管进行掘进爆破作业时的测振数据。此次爆破所用炸药为乳化炸药,药卷参数为Φ32 mm×320 mm×300 g(直径×长度×质量),电子雷管段间延期间隔设置为150 ms。炮孔连线如图1所示。一次循环爆破炮孔数目50个(其中,一圈掏槽眼4个,二圈掏槽眼10个,辅助眼17个,周边眼19个),一次循环爆破消耗总药量66 kg,全断面一次起爆,最大单段起爆药量16.2 kg,循环进尺2.1m左右。图1中,电子雷管采用段间延期共7段,段间延时间隔均为150 ms,图例中标号为对应段数,爆破顺序按图例从左往右,从上到下依次爆破。

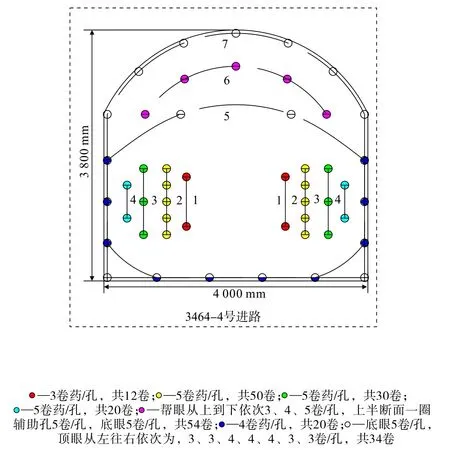
图1 爆破参数统计示意Fig.1 Schematic of blasting parameters statistics

2.3 监测点布置方案

本研究测试采用四川拓普公司生产的iSensor系列三通道智能传感器,该型传感器精度符合国家A级标准,分辨率为16 bit,数据采集精度高,基本不会对分析结果造成影响。仪器采集参数设置:连续采集模式,负延时长度256 ms,采集时长10 s,采集段数设置为65 535段,为最大采集段数,通道量程40 g,仪器固定内置采样率为4 000 Hz,设置出窗内触发,自动触发电平,运用离线采集模式。共选用6台测振仪器,所设采集参数均相同,待离线采集结束后连接终端设备进行数据下载。

本研究采用直线布孔的方法,沿巷道底板中心线布设(图2),第1监测点距离掌子面35 m,相邻测点传感器间隔5 m,根据测试场地的条件决定安设仪器的台数,每次监测不少于3台,不多于6台,传感器X轴指向爆心。

图2 3464-4号进路测点布置Fig.2 Survey point arrangement of No.3 464-4 roadway

3 振动监测结果及初步分析

本研究共进行了4次爆破测振,4次均为出矿进路的掘进爆破,具体测振结果见表1,典型的电子雷管振动速度—时程曲线如图3所示。

表1 爆破振动测试结果Table 1 Blasting vibration test results

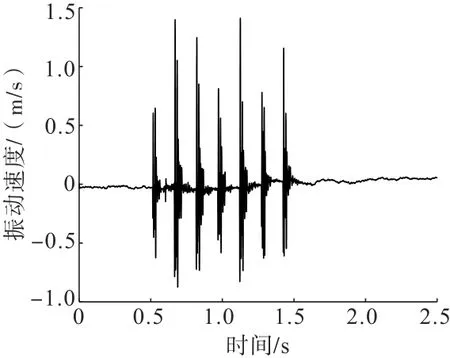
图3 电子雷管振动速度—时程曲线Fig.3 Vibration velocity-time history curves of electronic detonator

由表1可知:通过计算X、Y、Z各方向峰值振动速度均值,3个方向中水平径向较其他两向大,垂直方向次之,水平切向的振动速度峰值均值最小,其次,在几次测振试验中,各测点X轴方向峰值振动速度较其他两向呈现较为明显的规律性,即随着测点距离增加,峰值振动速度大体呈现逐渐减小的趋势。因此,进行爆破参数设计时,可参照爆破振动安全判据中的安全允许振动速度,以水平径向峰值振动速度为基准进行。由于此次掘进爆破使用了7段电子雷管,故波形图(图3)呈现出了峰值明显不同的7个波峰,且各波峰之间边界清晰,表示各段间并没有振动叠加现象的出现;第2、3、5、7段爆破产生了较大的振动,第1、4、6段振动较小,振幅最大值出现在第2段和第5段。

4 基于HHT法的信号处理与分析

4.1 信号小波软阈值法去噪

小波分析能够进行时频局部化分析,且进行滤波时具有小波基可灵活选择的特点。小波软阈值法消噪与小波强制消噪、默认阈值法消噪不同,设定软阈值去噪时,不容易丢失原始信号的有用成分,使消噪结果更具有可信度。本研究采用小波软阈值法消噪,选用“db5”小波基进行5层分解,并提取小波分解系数,给定消噪软阈值,依次处理其中超出经验设定阈值的系数,以达到消噪的目的,最后通过小波逆变换,重构去噪后的信号。消噪前后的信号对比如图4所示。

图4 信号去噪前后对比Fig.4 Comparison of signal before and after denoising

4.2 延期时间识别及延期方法比较

通过EMD法和瞬时能量法分别对电子雷管的实际延期时间进行了识别,并对两种方法的延期识别精度进行了比较。EMD法与瞬时能量法目标识别对象上有较大不同,瞬时能量法的分析对象为原始信号整体,而EMD法的分析对象为能够最大程度代表原始信号的分量,即某个IMF主分量。可见,EMD法精确了识别对象,减少了原始信号中的干扰部分,在对雷管段数识别中具有突出优点。但该方法由于在分解过程中,各IMF分量之间容易出现模态混叠现象,在延期时间识别精度方面有待进一步提升。

通过EMD法分解得到的IMF1信号包络图如图5所示,原始信号的瞬时能量图如图6所示。整体来看,图5、图6均展示7个幅值大小不同的主要波峰,与此次爆破所选用的7段电子雷管相对应。通过Matlab软件标点,显示图5中各波峰对应时刻分别为0.533 0、0.671 8、0.822 7、0.968 8、1.121 0、1.293 0、1.425 0 s,对应的延时间隔分别为0.138 8、0.150 9、0.146 1、0.152 2、0.172 0、0.132 0 s。图6所示瞬时能量法识别的各波峰对应时刻分别为0.495 0、0.676 5、0.827 5、0.986 0、1.119 0、1.270 0、1.409 0 s,对应延时间隔为 0.181 5、0.151 0、0.158 5、0.133 0、0.151 0、0.139 0 s,通过图谱显示EMD法和瞬时能量法对7段雷管均能准确识别,段数识别率为100%。在延期时间识别精度方面,根据本次使用的电子雷管段间延期均为150 ms计算,EMD法识别的延期时间最大正误差为+22 ms,最大负误差为-18 ms。瞬时能量法识别的延期时间最大正误差为+31.5 ms,最大负误差为-17 ms,识别误差较大。此次使用的是新疆雪峰科技生产的数码电子雷管,满足延期150 ms内误差小于1.5 ms的精度要求,且使用的是iSensor系列三轴智能测振仪,测试精度满足国家A级标准,以上两种因素基本不会对分析结果造成影响。

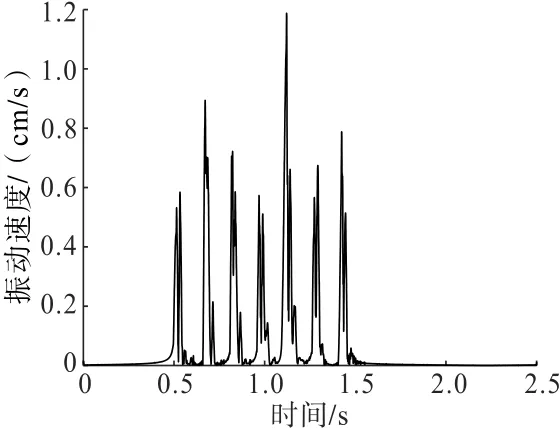
图5 分量1信号包络图Fig.5 Envelope diagram for component 1 signal

初步分析,造成EMD法延期识别出现误差的原因为,EMD分解得到的IMF分量受到外界因素干扰,出现了模态混叠现象,使得识别的包络图谱出现多余波峰。因此实际运用时,需结合现场具体设置的延期时间,对应包络图谱中最接近的波峰进行识别,以此提高识别精度。图5中在每段最高波峰附近,约20 ms各段均出现了临近波峰,且幅值除了第5段外差距都很小,结合爆破现场实际设置的延期时间,在幅值相差不大的前提下,选择合适的波峰,识别到的波峰时刻分别为0.514 2、0.671 8、0.822 7、0.968 8、1.121 0、1.274 0、1.425 0 s,延时间隔分别为0.157 6、0.150 9、0.146 1、0.152 2、0.153 0、0.151 0 s,计算得到识别的最大正误差为+7.6 ms,最大负误差为-3.9 ms。经计算,EMD法延期时间识别精度为95.2%,较瞬时能量法82.6%的识别精度已有很大的提高。初步分析,若能够对EMD法进行优化,使其能够进行完全正交分解,可在很大程度上消除EMD分解过程中的模态混叠现象,分析经过完全正交分解后,EMD法的延期识别精度将大大提高。

5 振动信号的时频能量谱分析

5.1 信号EMD分解与分析

振动信号经验模态分解后,各IMF分量的能量分布如图7所示。因EMD分解是将原始信号从高频到低频逐层分解,故得到一组振动幅度逐渐减小、频率逐渐降低的IMF分量,其中IMF10为信号残余分量。结合图7分析可知:IMF1分量振动幅度最大,且波形特征与原始信号最为接近,从振幅和所含的能量上看,IMF1～IMF3为信号的主要成分,其余分量随着分解频率逐渐降低,所含能量逐渐减少,振幅逐渐降低,波形曲线拉长,逐渐失去了原始信号的特征,为信号的次要部分和低频成分,IMF10作为信号的残余分量一般予以忽略。由经验模态分解结果可知:主要分量IMF1的优势频率为120～170 Hz,IMF2的优势频率为50～100 Hz,IMF3的优势频率为20～50 Hz,这3个主要分量在更大的频带范围内也有较多能量分布,其余次要分量主要是信号的低频成分,频率一般小于40 Hz。

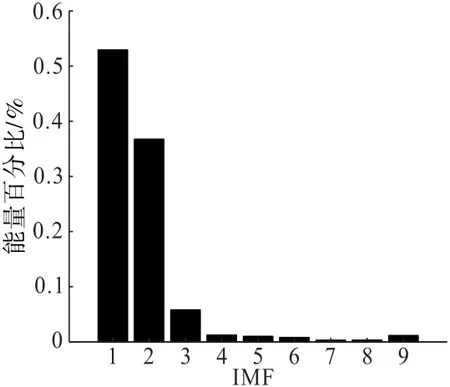
图7 去噪后各分量能量分布Fig.7 Energy distribution of each component after denoising

5.2 三维Hilebert谱分析

Hilibert变换在一定程度上剔除了原始的噪声部分,进一步地,在剔除EMD分解得到的残余分量后,将其余所有的IMF分量进行Hilbert变换,可得到三维Hilbert谱。该图谱能够清晰地反映时间—频率—能量三者之间的分布特征。

爆破振动信号三维Hilbert谱如图8所示,可见振动信号的大部分能量分布于0～200 Hz,大于 200 Hz的频带内含有的能量很少,这与几个IMF主分量的主频带范围基本一致。观察爆破振动信号的三维Hilbert谱可以看出,时间—能量平面内出现了7个边界清晰的能量峰值,各峰值所在的时间点与瞬时能量谱所识别的各段雷管爆破的时间点一致。在第5段爆破,即1.121 s时,产生了此次爆破的能量峰值,此外,在较低频带(0～20 Hz)能量持续时间最长,在整个低频带范围内均分布着部分能量,在高频段(2 000 Hz左右)分布着一些能量,初步分析为外界干扰造成。以往对于爆破振动信号的分析手段大多为傅里叶变换法或小波变换,且分析对象局限于振动产生的频率和能量。以往研究表明,振动信号的能量具有时间累积特性,在分析时应充分考虑时间因素的影响,HHT法能够将能量随频率和时间的变化规律展现在三维Hilbert能量谱中,这使得所展示的振动信号特征更加全面和形象。

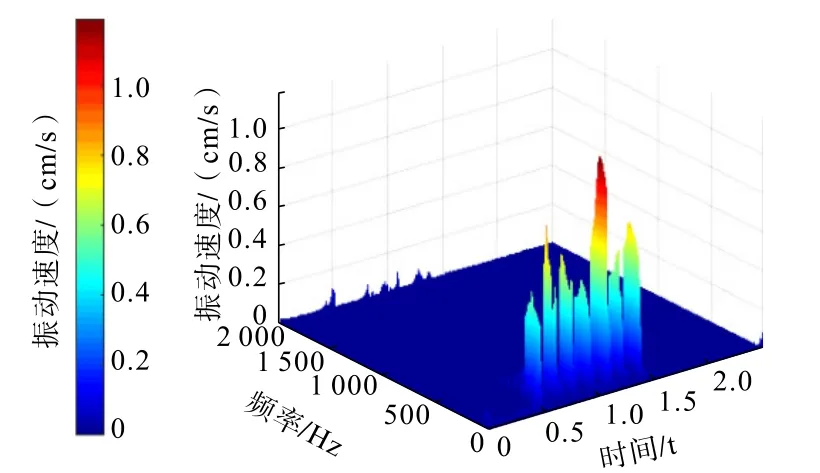
图8 爆破振动信号三维希尔伯特谱Fig.8 Three-dimensional Hilbert spectrum of blasting vibration signal

5.3 信号的边际能量分布特征

对Hilbert谱在时间上进行积分,可以得到振动信号的边际图谱,如图9所示。该图谱表示爆破振动产生的能量在时间范围内累加,其含义是各频率在整个爆破活动下的累加能量值,能够清楚地反映能量在各频率上的集中程度。

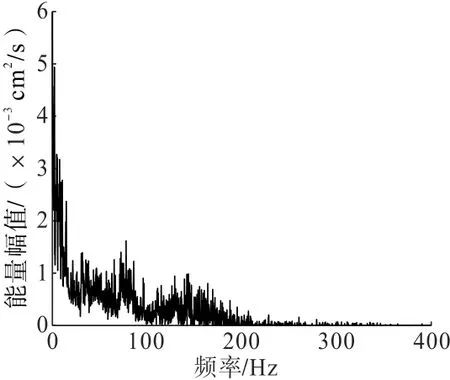
图9 信号边际谱Fig.9 Signal margin spectrum

由图9可知:此次爆破振动的主要能量频段小于50 Hz,在 0～12 Hz范围内出现多个幅值较高的能量峰,且占总能量的比值较大,说明此次爆破频率朝向低频方向发展,在50～100 Hz和100～200 Hz频域范围内也有部分能量分布。为便于更加具体地展示各频段携带的能量大小,划分了 0～10、10～50、50～100、100～200 Hz和大于200 Hz 5个频带,分别在这5个频带范围内对频率进行积分,可得到各频带能量占比大小,如图10所示。该测点5个频带能量占比见表2。由表 2可知:0～200 Hz频带携带的能量高达99.22%,说明此次爆破产生的能量基本分布在0～200 Hz,与三维能量谱和功率谱分析结果一致。0～50 Hz频带携带的能量占总能量的78.08%,说明0～50 Hz为此次爆破的主振频带。

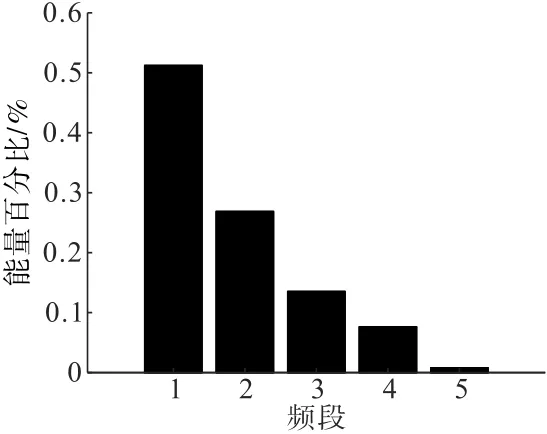
图10 边际谱频段能量分布Fig.10 Distribution of energy of the marginal band

表2 各频带能量百分比Table 2 Percentage of energy in each frequency band %

Hilbert二维线性谱如图11所示。由图11可知:能量基本全部分布在0～200 Hz,在 0～50 Hz频带内含有大部分能量,能量分布最多的频带为0～10 Hz,这也与前文分析一致,再次佐证了HHT法对振动信号分析的适用性。

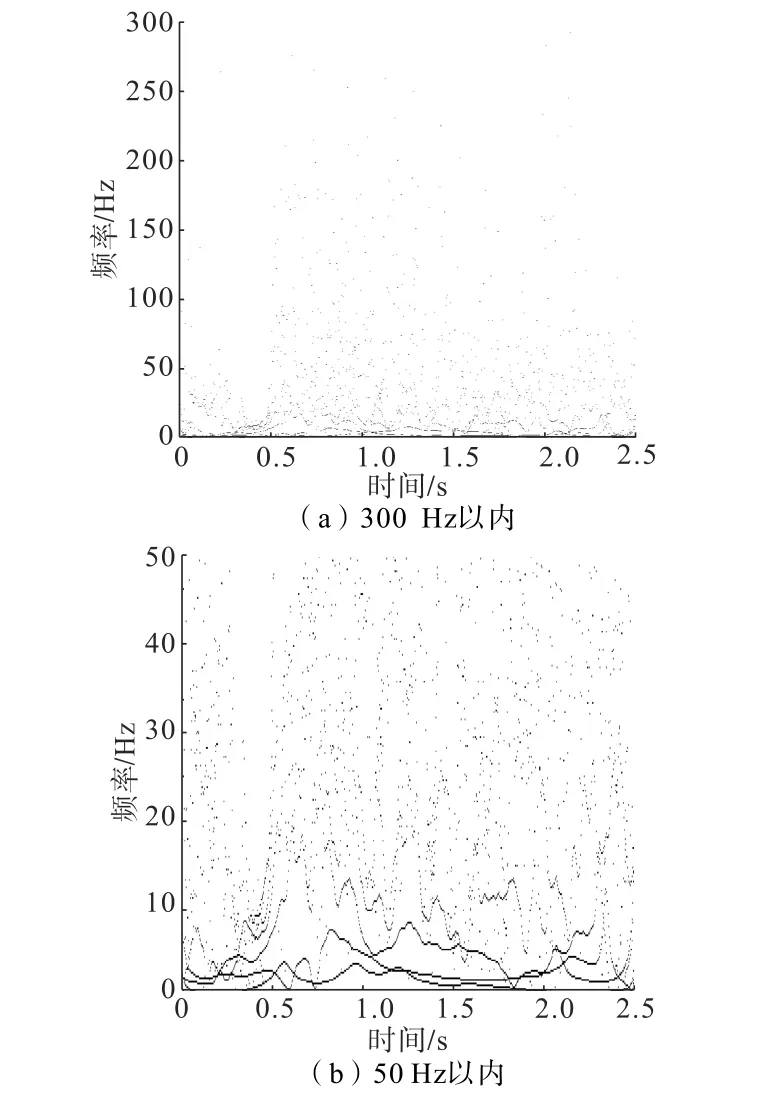
图11 希尔伯特二维线性谱Fig.11 Hilbert two-dimensional linear spectrum

研究发现,当质点振动速度较大时,振动频率也相对较大,这样不易与建筑物发生共振;当质点振动速度较小时,振动频率也相对较小,容易与建筑物发生共振,对建筑物的危害较大。这就要求当质点的频率较小时,振动速度需小于其相应的规定安全阈值,根据以往工程经验确定的爆破振动安全振速范围见表3。此次爆破在0～10 Hz频带内含有51.22%的能量,需验证此低频带的安全振速阈值。

表3 岩石边坡与矿山边坡爆破安全振动速度范围Table 3 Safe vibration speed range of the rock slope and mine slope blasting (cm/s)

由表3可知:当f≤10 Hz时,矿山边坡和矿山巷道安全允许质点振动速度范围分别为3.0～4.0 cm/s和15～18 cm/s。因此,为同时确保矿山巷道和边坡安全,选取该区域建筑物的最大安全允许振动速度为3.0 cm/s。虽然此次爆破最大振动速度仅为1.405 6 cm/s,在安全允许振动速度范围内,但此次爆破在1、3.2、5.4 Hz分别出现了能量峰值,且幅值较大,与一般建(构)筑物的自振频率非常接近,虽然振动速度较小,也极可能引起建(构)筑物的共振,在今后爆破作业时需重点关注0～10 Hz低频带,并采取措施减小低频能量带来的安全隐患。

5.4 信号的瞬时能量特征

图6所示的瞬时能量分布图显示,在不同时刻瞬时能量出现多个峰值,这是采用多段别雷管爆破所产生的现象。由图6可知:能量大部分集中于0.4～1.5 s,与原始信号一致,各段峰值一一对应7段雷管爆破,其中最大瞬时能量出现在1.119 s,为第5段雷管爆破,对应底眼、帮眼和第1圈压顶眼的爆破。结合图1分析可知:此段爆破共用54卷乳化炸药,虽然有前几段爆破所产生的爆破自由面,但此段爆破所消耗的炸药量远高于其他6段,因而产生了较大的能量,在不影响爆破效果的前提下,现场爆破作业时应注意减小此段爆破的炸药用量,有利于减小爆破振动。图6显示在0.495 s也产生了较大的能量峰值,为第1段雷管爆破,对应第1圈掏槽眼爆破,爆破所产生的能量仅次于第5段,虽然消耗的炸药量比其他6段小得多,但产生的能量却仅略低于第5段雷管爆破。原因是第1段为第1圈掏槽爆破,爆破时未提供爆破所需的自由面,受岩石的夹制作用较大。建议现场爆破作业时沿巷道中心线两侧一定距离,钻凿2～4个直径大于装药孔的空孔,以提供爆破所需的自由面,该措施可有效提高爆破效果,降低爆破振动。