在线校正的无人车五次样条实时路径规划方法*

张立雄，郭 艳，李 宁，宋晓祥，薛 端

（陆军工程大学，南京 210001）

0 引言

目前，依靠传感技术和信息技术的进步，无人车的研制已经取得了巨大进展，其智能化水平不断提高。国外研究的无人车主要基于感知、决策、规划、控制等模块实现。相比于欧美国家，我国的无人车研究虽然起步较晚，但是也取得了长足的发展，所研发的无人车已经具备了高精度地图、定位、感知、智能决策与控制等模块。无人车具有无人操纵的低风险性、可协作性、机动性强等优点，可大大缓解交通系统的运行压力，也可以执行复杂危险的军事侦察任务，避免发生人员伤害。

无人车是当前国内外人工智能研究的重点领域，而路径规划是其得以实现的关键技术。无人车路径规划的技术路线源自于轮式机器人技术，在保持全局导航规划的同时，无人车依靠传感器获取周围的行驶环境信息及车辆的状态，路径规划系统依此信息规划，并实时更新安全可行的路径以完成相应的行驶任务。

无人车的路径规划旨在满足路径平滑度、连续性、安全性、乘坐舒适性和车辆运动学约束等方面。路径规划算法主要分为3 类：启发式搜索方法、随机采样方法和数值优化方法。基于启发式搜索的方法通常是将路径规划问题转化为优化问题，对最优解进行搜索。LUO Q 等针对蚁群算法存在的易陷入局部最优、收敛性差、搜索效率较低等问题，提出了一种改进的蚁群算法，根据中间点与初始点、目标点的距离将初始信息素非均匀分布，减少了初始阶段的盲目性问题，在迭代中减弱启发式函数的作用，以加快收敛速度，通过增加惩罚因子减少丢失蚂蚁数量，保证了算法的多样性。LI J 等设计了一种混合路径规划算法优化无人车的行驶距离，采用遗传算法生成全局路径，根据局部滚动优化算法不断优化遗传算法的结果。启发式搜索方法可以根据具体的约束条件进行复杂的算法设计，但是优化过程通常需要耗费较多的时间。

随机采样方法是在地图上生成可行驶区域，以起始点为基点进行采样，生成大量的候选路径，从中选取最佳的路径。HU X 等采用三次样条曲线对地图上的道路中心点进行拟合，根据弧长和与中心线的偏移量生成大量候选路径，并且在考虑静态安全、舒适性和动态安全等因素的条件下设计了成本函数，根据总成本最小原则选取最优的路径。快速探索随机树（RRT）算法可以找到与目标点重合的一条路径，但路径的平滑性通常无法保证。随机采样法生成的大量路径可能包括较多的冗余路径，容易造成计算资源的浪费，而且找到的路径可能并非是最优的。

然而，为了保证车辆的稳定性和安全性，获得具有连续曲率的路径是有必要的。数值优化方法是根据路径规划的初始状态生成轨迹，通常考虑车辆的状态和受到的外部环境约束，并衡量每个目标的重要性，根据实际需要使设计的目标函数最大化或最小化，完成对生成轨迹的参数优化，路径规划中的优化问题通常可以转化为半无限约束规划问题。例如，文献［7］使用模型预测控制（MPC）来获得符合车辆运动学的路径。在文献［8］中，路径规划问题被转化为凸优化问题，在每个运动状态下都需要进行目标函数的高维度优化。数值优化方法为无人车的路径规划提供了很好的解决方法，然而优化方法的实时性难以保证。在CPU 上处理优化问题需要较多的时间，查找表的建立可以减少参数优化过程中花费的时间，但参考空间中的方向变化范围是有限的，这导致查找表无法直接应用于方向变化较大的路径规划中。

因此，无人车在时变行驶环境中，需要保证路径规划的乘坐舒适性、稳定性、实时性和连续性，为解决上述问题，提出了一种在线校正的无人车五次样条路径规划与实时优化方法，通过完成对五次样条曲线的路径优化，根据优化结果设计基于映射查找表的动态迭代路径规划方法，从而快速地规划出符合要求的路径。

1 主要工作

为解决无人车在路径规划中需同时满足乘坐舒适性、稳定性、实时性和连续性的问题，本文将五次样条曲线的生成方法作为路径的求解原理，在此基础上进行参数优化，根据乘坐舒适性、稳定性和执行效率的要求，以平均曲率最小和距离最短为目标，设计了路径优化的目标函数。其中，考虑到横纵向的速度、加速度和横摆角速度的限制，设计了路径优化的约束条件。针对参数优化问题，采用了序列二次规划（sequential quadratic programming，SQP）算法进行求解。

优化过程通常需要耗费较多的时间，将基于SQP 算法在一定方向变化范围内进行参数优化的结果存储并建立映射表，利用映射表查找法来解决路径优化的实时性问题。针对路径规划时起止点的方向变化超过映射表最大方向变化范围的问题，采用迭代更新规则对初始路径进行分割，便于直接根据分割后的起止状态信息，通过映射表查找法快速地规划路径，并保证路径曲率的连续性。

主要工作架构如图1 所示。

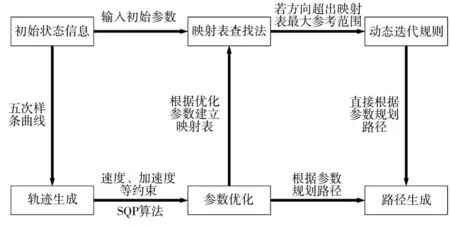
图1 主要工作架构

2 基于五次样条曲线的路径优化

2.1 求解原理

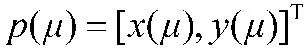
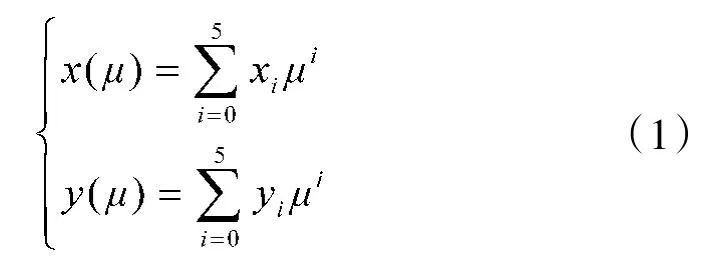
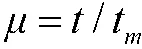
与路径纵向偏移量有关的各系数为：

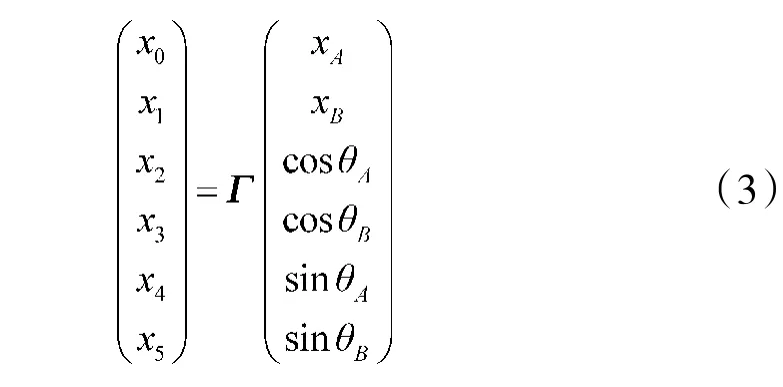
与路径横向偏移量有关的各系数为：

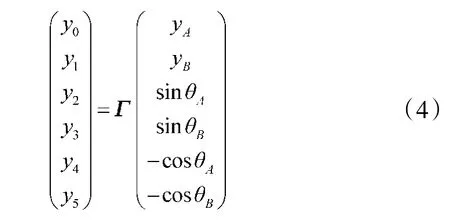
其中，θ及θ分别是初始点和目标点处的方向角；κ和κ分别是初始点和目标点处的曲率；η为无人车在初始点处的速度v；η表示无人车在目标点处的速度；η表示无人车在初始点处的加速度；η表示无人车在目标点处的加速度。

2.2 目标函数及约束条件

为使得无人车在行驶过程中满足乘坐舒适性和稳定性，应使得路径的平均曲率尽可能小。同时为提高行驶的执行效率，无人车总是希望以最短的距离完成行驶任务，因此，参数优化的目标函数设计为

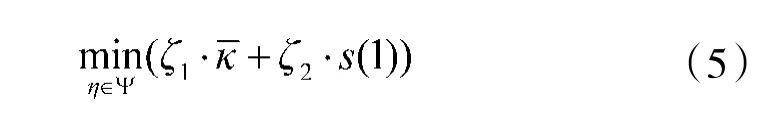
约束应满足如下：

其中，s 为沿着路径p（μ）测量所得的距离。

其中，ζ和ζ分别为路径平均曲率和距离在目标函数中所占的比重，由于无人车在行驶过程中更注重乘坐舒适性，因此，取ζ=10 000，ζ=1。式（6）是为了保证路径曲线的规律性。显然，η 表示路径距离s（或ds/dμ）的变化率：

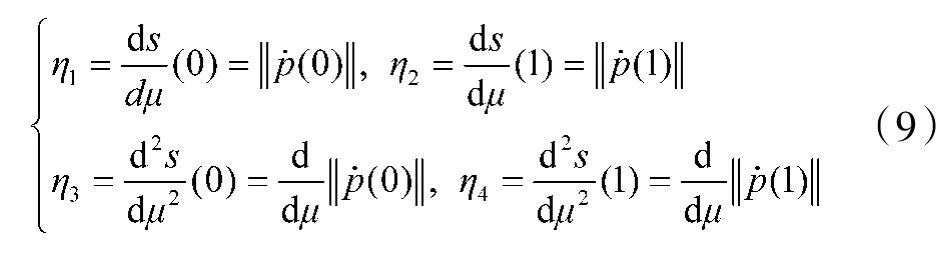
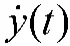
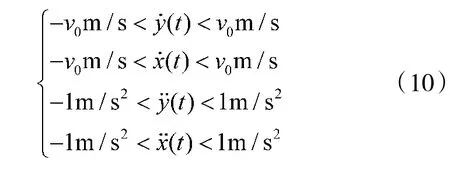
无人车在行驶过程中，需要考虑自身的稳定性。无人车的横摆角速度是反映车辆行驶稳定性的主要指标。假设无人车的质心侧偏角近似为0，那么需考虑无人车分别在横向和纵向上的横摆角，近似为

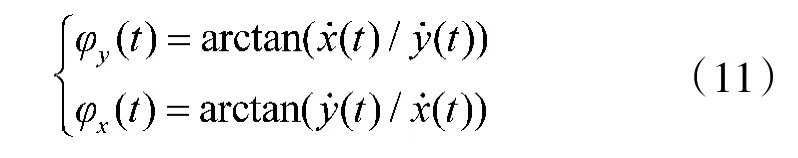
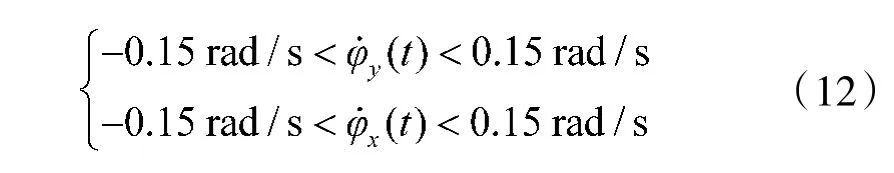
因此，通过上述目标函数和约束条件，通过调节参数，可以规划出符合乘坐舒适性、稳定性和执行效率且平均曲率最小的较短路径。

2.3 参数优化方法

极值优化问题可以转为半无限规划形式，将其转化为一组具有峰值的有限约束，这种优化问题一般可以通过序列二次规划（SQP）算法求解。SQP算法通过将具有非线性约束的原优化问题转换为在迭代点处的二次规划子问题，求解子问题获取新的解点，利用新的解点在原优化问题上再次利用二次规划求解。过程如下：

对于非线性约束的规划问题，一般由以下公式表示。

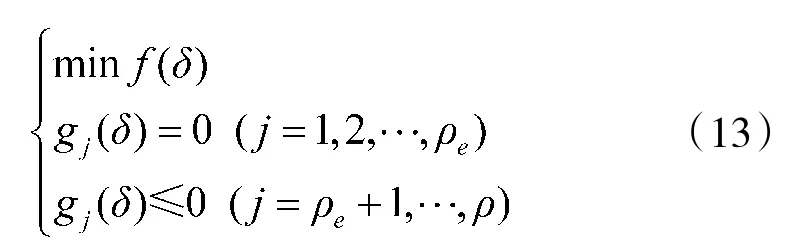
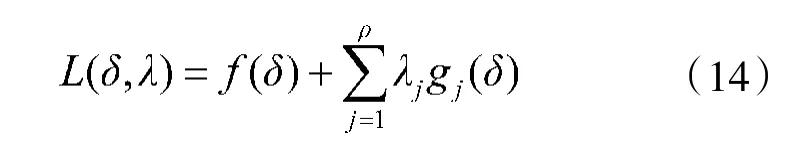
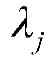
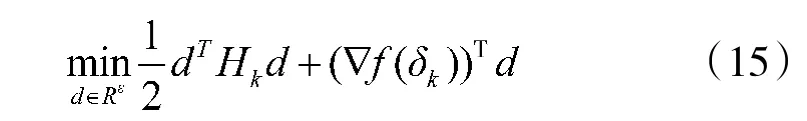
约束为：

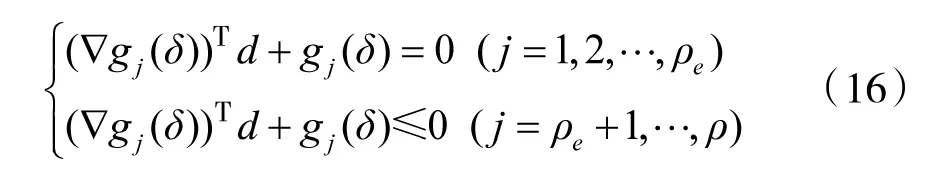
其中，d 是全局搜索变量； 是梯度；H是拉格朗日函数的Hessain 矩阵的正定拟牛顿近似值。通过稠密半正定牛顿近似法求解，式（15）可以通过任意一种QP 算法得到结果，所得的解将被用于新的迭代过程中：

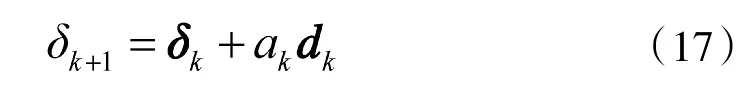
其中，d是δ指向δ的一个向量；a为标量步长，通过适当的线性搜索过程来确定，从而使函数的某一个指标达到足够小的减小量。

由于SQP 算法是目前公认的适于解决具有非线性约束优化问题的方法，相比于其他的优化方法，它具有计算效率高、收敛性好、边界搜索能力强等优势，故此选用该方法针对本文中的非线性约束优化问题进行参数寻优。

3 基于映射查找表的动态迭代路径规划方法

3.1 映射表查找法

由于求解路径优化问题需要大量的计算，时效性不足会导致优化方法在实际中难以实用。为了解决该问题，在实际应用中，映射表查找法可以为此提供解决方案，查找表由多维参数构成，包含起始和目标的位置、方向和曲率等参数。

由于每个参数都有无限的值，因此，有必要减少参数的维度并释放存储空间，于是构造起点和目标点分别固定在（0，0）m 和（10，0）m 处的参考空间。利用五次样条曲线进行插值的参数被简化为4 个自由度参数η：=［ηηηη］。通过查找表进行路径规划的过程如下：

1）形式转换

为了将初始点A 和目标点B 映射为位于参考空间中的A'和B'，端点的方向和曲率将转换为

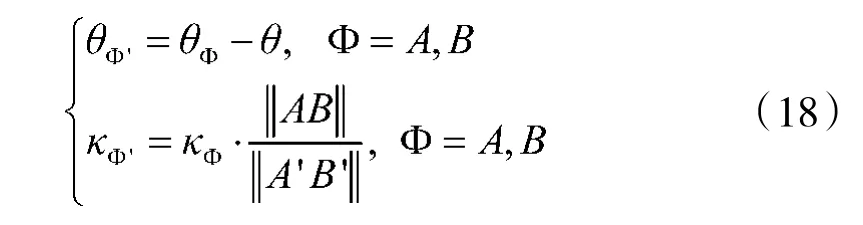
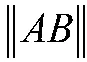
2）查找表

3）反转换

将从参考空间中获得的路径反变换为原始坐标系。反转换的过程如下：

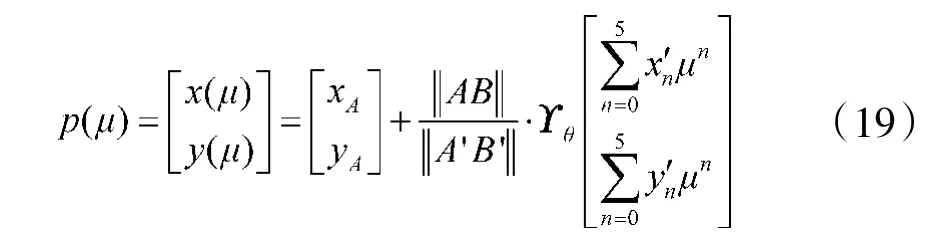
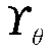
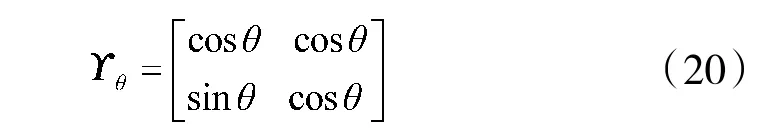
3.2 迭代更新规则

当方向变化超过查找表参考空间的最大范围［-θ，θ］时，很难直接将查找表应用于路径规划，因此，本文提出了一种迭代更新规则。该规则是选择曲线上μ=β 处的点作为路径分割点C，并将分割点作为下一条路径的初始点，分割点处的曲率为

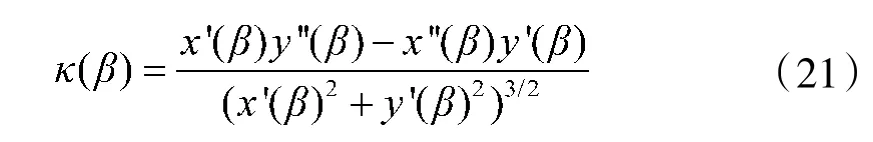
其中，β∈［0，1］为迭代更新率。因此，在动态路径规划过程中，通过更新初始点，可以得到完整的路径。

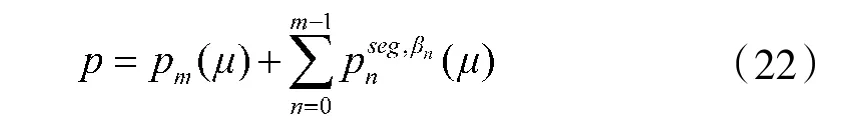
其中，m 表示路径分割的段数；β表示第n 段路径的迭代更新率。在路径生成过程中，这些分割点会导致车辆运动状态的大量变化。

1）最佳分割点搜索

具体的分割方法为：对β 从0 开始以速率r 增加的方式进行搜索，直到曲线的方向变化小于或等于2 θ，确定β 的当前值β，那么可以确定分割点C的位置。若考虑直接使用映射表查找法进行路径规划，那么所选用的迭代更新率应小于或等于β。

2）在线校正参数

完成路径分割后，此时就可以得到各段路径的起止点状态信息，其中，分割点处的曲率信息可通过式（21）计算得到，将起止点状态信息输入到映射表中获取最优的新参数，完成参数更正，从而快速地路径规划。

4 仿真分析

为了验证算法的有效性，对路径进行了优化求解，然后利用映射表查找法和迭代更新规则快速规划路径，并对路径规划的准确性进行了验证。路径规划的所有实验均是在Intel Core i7-10750H CPU 2.60 GHz 16GB RAM 上进行的，算法是基于MATLAB 软件编译实现的。

4.1 路径优化求解

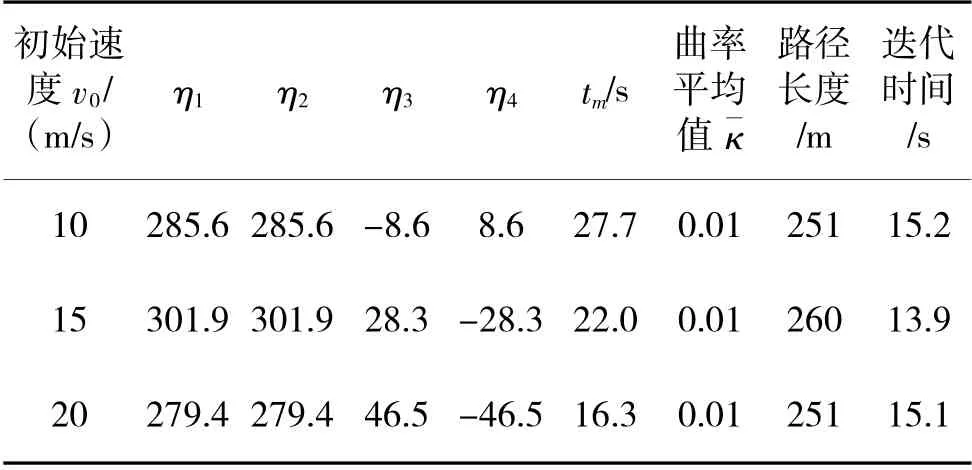
表1 优化结果

将获得的上述参数代入五次样条曲线中，得到的路径为：

v=10 m/s 时：

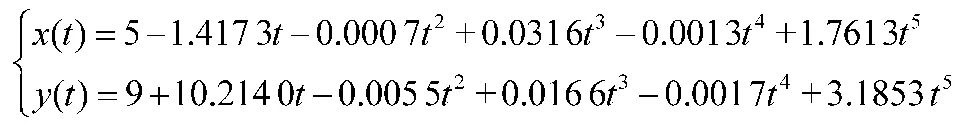
v=15 m/s 时：

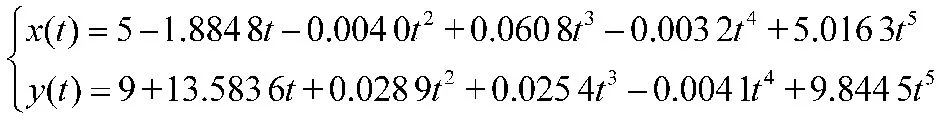
v=20 m/s 时：

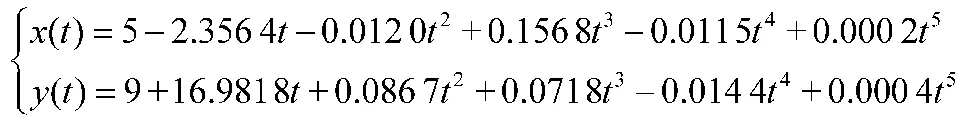
由表1 可知，基于SQP 算法进行参数优化的平均所用时长为14.7 s。然而，在同等的实验条件下，若使用基于虚拟编码策略的遗传算法对目标函数进行优化，需要的时间为数个小时以上。可见，相比于遗传算法，SQP 算法的计算效率有着较明显的优势。然而，对于无人车实际的应用，数十秒的优化时间仍然很长，难以满足路径规划实时性的要求。

4.2 路径实时生成及精度验证

为解决上述路径规划的实时性和查表法不可直接使用的问题，基于映射表查找法和迭代更新规则进行路径规划。

取4.1 节中初始速度为v=10 m/s 时得到的路径为初始路径，该路径的方向变化超过了参考空间的最大方向限制。对于该初始路径，仅需找到一个分割点即可通过映射表查找法直接而快速地规划路径。根据3.2 节中的分割方法，β 从0 开始以0.01的速率增加对分割点进行搜索。在仿真中，确定的迭代更新率为0.66，得到的分割点状态为p（C）=［56.1，163.0］，θ=10.6°，κ=0.032。得到的两段新路径分别命名为Path 1 和Path 2，根据两段新路径的起止点状态信息，基于SQP 算法进行参数优化，从而得到两段优化后的新路径，以便于验证映射表查找法的精度。为此，根据初始路径的端点A、B 和分割点C 的状态信息，可基于映射表查找法快速地规划路径，将所得路径与基于SQP 算法优化的路径进行了对比，如图2 所示。可见，基于映射表查找法得到的路径与优化路径几乎完全重合。

图2 路径规划

同时，对路径的曲率、曲率变化和多项式系数进行了对比分析，如图3 和图4 所示。

图3 基于查找表和优化结果得到的曲率κ 及其变化dκ/ds 的比较

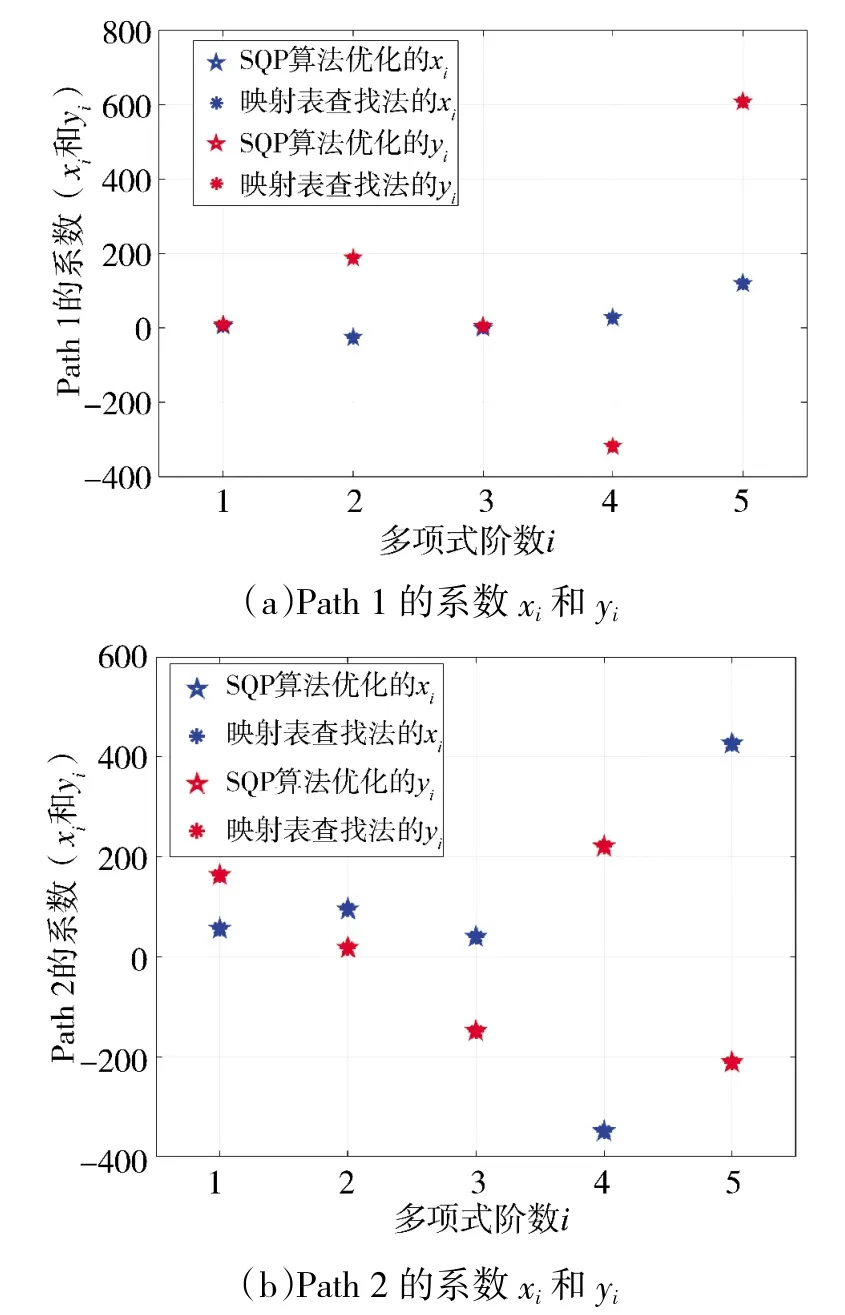
图4 基于映射查找表和优化结果得到的多项式系数xi 和yi 的比较

由上图可得，基于映射表查找法的路径规划性能与SQP 算法的优化结果非常接近，这说明了所提方法在路径规划中具有很好的效果，不需要复杂的优化过程，可以进一步缩短路径优化的时间消耗。

5 结论

本文针对无人车路径规划在时变行驶环境中对乘坐舒适性、稳定性和执行效率的要求，在考虑速度、加速度和横摆角速度等约束条件下，以平均曲率最小和距离最短为目标设计了目标函数，并基于SQP 算法对路径进行了优化。然而路径优化过程尚不能满足实时性的需求，且现有查表法的方向变化范围是有限的，为进一步提高无人车在行驶时的路径规划效率，提出了一种基于映射表查找法的动态迭代路径规划方法，该方法用于无人车路径规划中基于查找表的参数优化和最大方向变化超过查找表极限时的在线校正。结果表明，该方法具有良好的效果。