基于分层距离变换的铁路沿线立交通道线路优化

2022-10-22严伟谢淑敏徐占军蒲浩李伟申泽春谢春玲

铁道科学与工程学报 2022年9期

严伟，谢淑敏，徐占军，蒲浩，李伟，申泽春，谢春玲

(1. 湖南中大设计院有限公司，湖南长沙 410075；2. 中南大学土木工程学院，湖南长沙 410075；3. 高速铁路建造技术国家工程研究中心，湖南长沙 410075)

铁路是国家的重要基础设施，是国民经济的大动脉，在我国经济和社会发展中起着难以替代的支撑性作用[1]。当前，我国铁路正处于飞速发展时期，全国铁路营业里程已达到了13.9 万km。然而，在铁路建设过程中，将不可避免地与城市和地区中密集的既有道路路网出现大量交叉。为了避免新建铁路阻断既有道路，同时确保既有道路的运输安全和通行能力，需要对既有道路的部分段落进行改移，并在交叉点处布设立交通道，实现公路与铁路的立体跨越。立交通道的布设在交叉点处受到交叉口的交叉角度、有效净空和线形等约束限制[2]，在时间和精力有限的情况下，工程师往往仅凭自身经验主观对比几个满足约束、控制投资的可行方案进行最终决策，可能导致更有价值的方案被遗漏。因此，迫切需要提出一个既考虑道路建设、路网交叉等各项约束，又满足节省工程投资目标的道路与铁路立交通道智能设计方法。道路与铁路立交通道优化属于线路优化框架下的一个类别，相较于2个固定端点之间的线路优化，还需要考虑路网交叉，与既有道路连接的增强约束。国内外对于道路与铁路立交通道的研究主要分为3 个阶段：第1 阶段，对于每一个道路交叉点，仅提供接近最优解的备选方案集，在有限的方案中进行比选，选择满足约束与投资成本的最优线路方案，该方法包含设计者的主观性和随机性。第2 阶段：提出数学解析法，例如变分法[3]、枚举法[4]、数值搜索[5]与线性规划[6]，但是地形的变化和复杂的约束条件难以用连续可导的显式函数表示，存在理论上的不足，在处理实际优化问题时存在局限性。在第3阶段中，随着启发式算法[7-9]的提出，遗传算法、距离变换算法和粒子群算法等开始运用于线路优化。与精确解法不同的是，启发式算法不依赖于显式函数。其中JONG[10]提出了一个基于遗传算法(GA)的高速公路线形优化(HAO)模型，将优化问题转化为生物进化中染色体交叉与变异过程。李伟等[11]提出一种基于双向距离变换的山区铁路线形优化方法。SHAFAHI 等[8]利用粒子群(PSO)算法求解在复杂情况下，给定的起终点之间的最优线路方案。吴敏等[12]在其基础上提出改进的粒子群算法，避免其早熟收敛的缺点，增加方案多样性。尽管这些有代表性的研究为本文工作提出了宝贵的参考，但是多集中在新建铁路和道路的线形优化上，且均为在2个固定端点之间寻找满足指定目标的最优解决方案，并不直接适用于立交通道的线形优化问题。对于立交通道而言，其线路的起终点，即与既有道路的2个连接点是非固定的。同时，立交通道与新建铁路在交叉点处的交叉约束、连接约束与几何约束也是在优化过程中必须要考虑的问题。为了解决上述问题，本文提出将线路的投资成本视为立交通道的起终点之间的特定距离，把立交通道的线路优化转换为起终点之间的最短路径搜索问题。针对道路与铁路立交通道起终点均不固定的情况，提出优化模型和解算方法用于铁路沿线立交通道线路优化，其主要贡献如下。

1) 构建一种考虑与既有道路连接点和铁路交叉点均可变的立交通道线路优化模型。

2) 提出一种基于距离变换(DT)[13]的分层优化策略，将问题分解为非交叉段子优化和交叉端与非交叉段2阶段重组，削弱连接点与交叉点的耦合相互作用。

3) 最后，将该方法应用于一个复杂的实际案例，通过对计算机与人工方案进行比较，验证该方法的有效性。

本文的第1节给出了铁路沿线立交通道线路优化模型。第2 节将DT 算法应用于立交通道问题。第3 节和第4 节分别提出了实际案例研究和本文结论。

1 优化模型

1.1 综合地理信息模型

确定研究区域的边界是建立地理信息的前提。如图1所示，在距离既有道路与新建铁路的交叉口位置I的X米处(本文X=500 m)，沿既有道路构造椭圆区域，识别椭圆焦点A，B2 点，取展线系数γ=2imax/iD为偏心率，其中，iD为地面高程的平均坡度，imax为道路的最大限制坡度。取研究区域为该椭圆的外接四边形，并将研究区域细分为宽度为w的单元方格。获取研究区域内各个网格的包括地形(高程)、地质(岩土特征)、单位成本(工程单价信息)、现有建筑(工厂、道路、铁路、居民区)等地理信息，构建综合地理信息模型(CGIM)。更多有关CGIM详细解释可见文献[14]。

1.2 决策变量

立交通道优化属于线路优化，利用起终点之间的一系列交点(PI’s)可以描述其三维线路[15]，具体分为平面交点(HPIs)和纵面交点(VPIs)的坐标。同时，立交通道中的桥梁和地下通道可以通过MBUs来定位[16]，与道路连接点和铁路交叉点通过VCCs表示，立交通道能通过I(与铁路交叉点)中连接点(VCCs)，S＆E(连接既有道路起终点)，结合HPIs，VPIs，MBUs，VCCs决策变量可表示为：

其中：XH，YH，RH，lH0和lH1分别表示平面交点的坐标、交点半径、前后缓和曲线长度；KV，HV和RV表示变坡点的里程、高程和竖曲线半径；KBS，KBE和KUS，KUE分别表示桥梁和隧道的起始里程与终点里程；I表示改建道路与新建铁路交叉点，S和E表示改建道路在既有道路上的起始连接点和终止连接点。

1.3 目标函数

铁路沿线立交通道线路优化模型的目标是寻找施工成本最低的优化设计。其中施工成本主要包括土石方工程费(CE)，路面成本(CP)，路权费(CR)，桥梁工程费(CB)以及隧道工程费(CU)，具体表示如下：

其中：CE，CP，CR，CB和CU的具体计算公式可见文献[17]。

1.4 约束

公路和铁路处的立交通道需满足4 种类型约束：几何线形约束(CGeometry)，交叉约束(CCrosse)，连接约束(CConnect)与《公路路线设计规范》(JTG D20—2017)中既有结构约束(CStructural)。

1.4.1 几何线形约束(CGeometry)

1) 平面几何约束：① 最小曲线半径(RHmin)；② 最大曲线半径(RHmax)；③ 最小夹直线长度(LHmin)；④ 最小转向角(αcmin)。

2) 纵断面几何约束：① 最小允许坡长(LVmin)；② 最大允许坡长(LVmax)；③ 最小竖曲线半径(RVmin)；④ 最大允许坡度(imax)。

1.4.2 交叉约束(CCrosse)

1) 道路与新建铁路相交时，形成的交叉角AC不应小于规定的最小交叉角Amin，并尽可能地使道路与铁路正交：

2) 为保证车辆的安全运行，立交通道处的净空(即铁路设计标高Hrail与道路设计标高Hroad之间的高差值)应满足如下约束：

3) 道路立交通道交叉部分必须保持笔直，以保证行车时的良好可见度。

1.4.3 连接约束(CConnect)

局部改建道路与既有的道路连接时，改建道路与既有道路在连接点处的方位角应一致：

1.4.4 既有结构约束(CStructural)

1) 禁区：取集合UF表示禁区单元格；集合UC为搜索路径所占用的单元格。为保证搜索路径绕避禁区，UF与UC的交集应为空：

2) 结构要求：桥梁的高度和长度，隧道的孔径应该满足《道路线形设计规范》(JTG D20—2017)中规定。

综上所述，铁路沿线立交通道线路优化模型可表示为：

2 搜索方法

2.1 分层优化策略

由于立交通道与新建铁路交叉点(I)和与既有道路的起终点(S和E)连接位置均是可变的(如图2所示)，其线形优化也因地形、地质、约束条件和优化目标而变化，因此关键问题是如何分解上述3种过程，并削弱耦合交互作用。将整个S→I→E路径以I为界分解为S→I，I→E2 段。故整个搜索转化2 个主要过程：1) 可变交叉点I处的路径拼接；2) 不同端点之间的路径搜索问题(S＆I，I＆E)。但如何在考虑交叉约束的情况下正确拼接S→I，I→E在I处的路径，并确定一个固定端点(I)和一个可变端点(S/E)之间的有效路径搜索方法是尤为重要的。为解决上述难题，提出：

1) 将新建铁路附近单元格定义为左侧单元格集合L[L1,L2, …,Lp]和右侧单元格集合R[R1,R2,…,Rq]。将新建铁路左侧既有道路穿越起点单元格定义为S[S1,S2, …,Lm]，同理，终点单元格定义为E[E1,E2,…,En]，具体可见图3。将S→I，I→E进一步分解为S→L，L→R，R→E。并对L→R交叉段路径进行交叉约束处理，完成在I点的路径拼接。

2) DT 算法可以生成任意单元格到目标单元格间的优化路径，故依次将L中单元格作为目标单元格，S中单元格为任意单元格，采用DT 算法搜索得到S→L的若干条路径。R→E段可行路径同理可得。

2.2 固定端点与可变端点间的路径搜索

取L[L1,L2,…,Lp]或R[R1,R2,…,Rq]中一个单元格为固定端点，S[S1,S2,…,Lm]与E[E1,E2,…,En]中单元格为可变端点。在满足第1.4 节所述约束条件的情况下，以L中一单元格Li和S[S1,S2,…,Lm]中单元格之间利用DT 进行路径搜索的过程为例，具体步骤如下。

第1步：对新建铁路线左侧的研究区域进行预处理。研究区域中的单元格应该满足高度可访问性，即研究区域任意一单元格(Rx,Ry,Rz)到固定端点Li(LRx,LRy,LRz)的距离必须保证在使用最大限制坡度imax和容许展线系数γ条件下，能够克服2单元格之间的高差，即满足：

如果有单元格未通过高度可访问性检测，即与式(11)冲突，则将该单元格标记为禁止单元格，后续的双向扫描过程中将忽略该禁区单元格的扫描。

第2步：初始化左侧研究区域所有单元格的广义距离值VDT，如式(12)所示，即固定端点(LR)为0，其他单元格(D)均为正无穷。广义距离表示将距离变化中的距离概念拓展到综合代价，即前述(CE+CP+CR+CB+CU)确定的综合造价，其值表示广义距离值。

第3 步：如图4 所示，利用正反双向扫描的方式从图像的左上角开始，按先正向(从下至上，从左至右)，再反向(从上至下，从右至左)的顺序扫描非禁止单元格，更新其广义距离值，形成最终的广义距离图。当单元格(G)被扫描时，将邻域模板的中心置于其上，遍历邻域模板中所有单元格(例：图4中单元格P)，对2单元格形成的局部线路判断是否满足第1.4 节所述的线形几何约束；桥梁的桥高约束、桥长约束与净空约束；根据线隧挖深分界标准自动布设生成的隧道是否满足隧长约束、地质条件约束；路基段是否满足坡度坡向要求和地质条件要求。当不满足条件时，剔除该局部线路，重新选择邻域模板内其余单元格，当单元格(P)满足：

则更新当前单元格P的广义距离值VDT(P)，使VDT(P)=VDT(G)+d(P→G)，并记录P与G之间的行列差(ΔR，ΔC)，以用于追踪优化路径。

第4 步：通过第3 步形成的广义距离图，寻找处于S集合内所有单元格的VDT值，将VDT值最小的单元格(Si)作为以Li为固定端点的最短路径终点，并通过ΔR，ΔC递推出单元格Si到Li的最短路径方案[11]。通过对L中单元格的迭代，可以得到从S中所有单元格到L中所有单元格的非交叉段优化路径。同理可得到R到E的所有非交叉段路径，如图5所示。

2.3 L至R交叉段拼接处理

通过迭代搜索单元格集合L与R之间局部线路的方法对交叉段进行处理，保留满足所有约束条件的局部线路方案。如图6 所示单元格Li为例，首先，在进行局部路径搜索之前，以铁路线的垂线作为角平分线，从单元格Li绘制角度为(π-2*Amin)的扇形，排除扇形区域外的R集合中单元格，剩余单元格与Li相连形成的局部线路一定满足交叉段的交叉角约束。然后，进一步对局部线路进行第2.4节中所述其他约束，若不满足，剔除该方案；若满足，刷新Li→Rj的广义距离值，生成局部线路的平纵面和桥隧线路方案。

通过上述步骤解决了2.1 节中提到的难题，并对2 个非交叉段和交叉段形成的局部路径进行组合，形成完整的线路方案，并对所有路径的广义距离值进行排序，选择最小距离值的方案为最优路径。对最优路径采用弦切支距法选取路径中的特征点作为平面交点，并根据规范匹配最小的圆曲线半径和缓和曲线长度，生成初始的平面线路；在平面初始线路方案基础上，根据土石方工程量最小初始化纵断面方案。

3 案例分析

3.1 工程概述

该方法已应用于湖北省汉江沙洋港疏港铁路与其沿线三级公路改建形成的立交通道作为研究案例。该例中研究区域被分成10 m 宽单元格，路径搜索过程中考虑第1.4 节中所述约束，具体数值可参见相关规范。并采用表1中记录的各类单位成本计算目标函数。

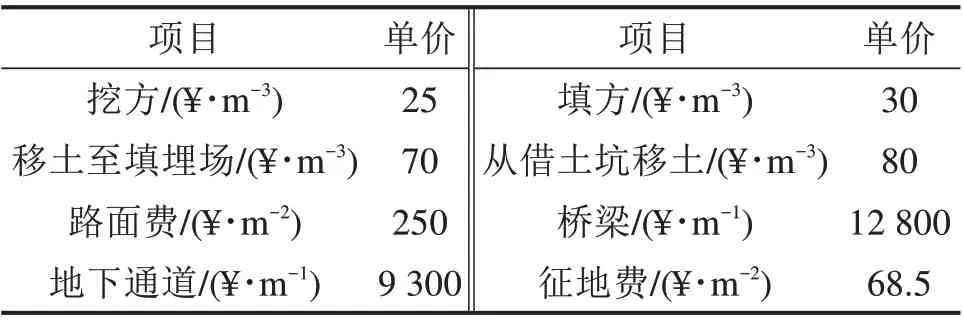
表1 单位成本信息Table 1 Unit cost information

3.2 优化结果

开发的程序在个人电脑(8核i7-7700CPU，16G内存)普通计算机上耗费396 s 生成187 条备选路径。所有路径均满足交叉点约束，并按工程造价排序。选择计算机最优方案(AC)为具有代表性的路径，并将其与经验丰富的工程师的手工方案(AM)进行对比，详细的平纵面对比如图7 和图8 所示，对比数据可见表2。

事实上，为了跨越铁路线，立交通道交叉位置通常有上跨桥梁和地下通道2种形式，该算例采用地下通道的形式。从平纵方案图和表2 可以看出，AC方案线路长304 m，相较于AM而言，减少了33 m，即9.8%。同时，从图8(a)可以看出，AM在穿越铁路时，为了保证列车的安全运行，需要保证道路与铁路之间至少存在4.5 m 的净空。对于AC而言，该方案在合理利用既有道路附近的地形条件，将填挖方量共减少47.5%的同时，在铁路上寻找到合适的交叉点，无需下挖涵洞即可满足净空要求，减少了地下通道的工程量，尽管其地下通道长度增加了2.6%，最终总工程造价减少了6.1%。