10 kV电缆熔融接头制作过程的热-力仿真分析

2022-10-21丁然袁超喻建梅睿田正兵梁栋张宝磊吴亚东

绝缘材料 2022年10期

丁然，袁超，喻建，梅睿，田正兵，梁栋，张宝磊，吴亚东

（1.江苏方天电力技术有限公司，江苏南京 211102；2.江苏中天科技电缆附件有限公司，江苏南通 214000）

0 引言

随着我国城市经济的快速发展，城市架空线逐渐淘汰，配电网电缆化的趋势在逐渐加快，电力电缆的投运量持续攀升[1]，对应的电缆故障率也在增长。统计结果表明，80%以上的电缆及附件系统故障发生在电缆中间接头处，远高于电缆本体的故障率[2-3]。

常见的电缆接头由于增强绝缘的材质与电缆的绝缘介质不同，不可避免地存在可活动界面，一方面可能导致电缆绝缘回缩或电缆接头主体移位，另一方面易产生电场畸变，加速界面附件的绝缘老化。而熔融接头技术是按照电缆的原始结构，使用与电缆各层相同材料逐层恢复制作，形成再生结合的一个新的电缆，可以解决电缆附件与电缆绝缘之间配装产生的不同绝缘介质界面的根本问题，并且无需应力锥、无活动界面的熔融结构。

熔融接头的制作存在以下4点问题：①产品安装对现场环境要求高；②产品制作时间长；③绝缘熔融接头制作过程中温升-温降易形成应力集中，影响其加压后的绝缘性能；④缺乏产品制作过程的检测手段。目前，国内外对于熔融电缆接头的研究较少，并且很少探究影响熔融接头制作过程应力的因素。唐科等[4]分析了接触电阻、电缆本体长度对10 kV三芯电缆接头温度分布的影响。李文祥等[5]通过理论推导低压配电三芯电缆并联结构的6层4节点稳态热路模型，利用外表皮温度计算电缆各层温度。对于绝缘接头的应力问题研究主要集中在接头过盈配合。田正兵等[6]通过Ansys建立110 kV交联聚乙烯（XLPE）电缆由硅橡胶制成的电缆接头有限元模型，研究了界面压力值沿电缆中轴的分布；还根据模型分析了电缆接头材料杨氏模量之间的关系。马永其等[7]以某类220 kV电缆终端为例，建立其应力分布的非线性三维有限元模型，为某型号电缆终端开发过程中橡胶材料和结构形式的选择提供了理论支撑。而对于熔融接头制作过程的研究上述文献均未提及。

本文提出研究电缆绝缘熔融接头制作过程的应力分布的仿真模型，通过控制变量法研究风冷与水冷两种方式的流体温度和流速对于电缆熔融接头应力分布的影响，以及新交联的交联聚乙烯与旧的交联聚乙烯的材料性能差异对其应力分布的影响，以期为电缆熔融接头制作提供参考。

1 建立仿真模型

1.1 电缆熔融接头结构模型与参数的确定

电缆熔融接头多应用于中压电网中，以10 kV电缆熔融接头为例，仿真模型如图1所示。

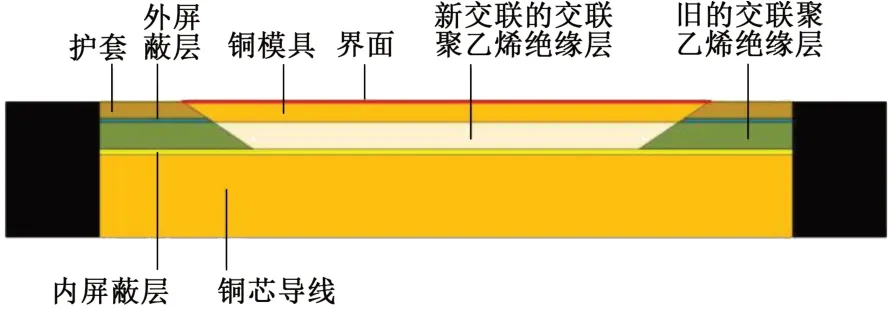
图1 电缆熔融接头仿真结构示意图Fig.1 Schematic diagram of simulation structure of cable fusion joint

熔融接头在制作过程存在交联聚乙烯绝缘层的加热-冷却过程，交联聚乙烯作为高分子材料，具有典型的粘弹性特点，对于冷却过程的应力主要研究形成的残余热应力，其本构方程采用积分型热粘弹性本构，基本假设如下：①不计结晶、取向、流动残余应力，聚合物的初始应力为零；②聚合物是各向同性的简单热流变型材料；③假设聚合物应力应变值足够小，可以用线性粘弹性本构方程描述。

本文根据研究问题的具体情况，从热粘弹性材料的基本特性出发，材料的主要力学性能参数如杨氏模量、剪切模量等均为温度和时间的函数，根据文献选择，交联聚乙烯材料的松弛数据参考文献[8]的试验结果，如表1所示，其中K为广义麦克斯韦模型的级数，gk为剪切模量，τk为松驰时间。

表1 交联聚乙烯松弛数据Tab.1 The relaxation data of XLPE

1.2 电缆接头物理模型

对于电缆接头的温度场分析问题，根据傅里叶传热定律和能量守恒定律，可以得到描述温度场问题的控制方程，在直角坐标系中可写成式（1）。

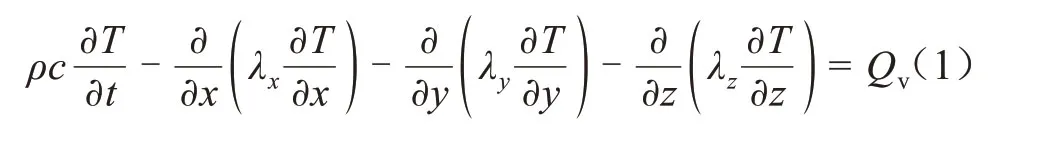
式（1）中：ρ为材料密度；c为材料比热容；T为待求温度变量；t为时间；λx、λy和λz分别为材料沿x、y和z方向的导热系数，对于同性材料有λx=λy=λz；Qv为物体内部单位体积产生的热量，即热源密度。

式（1）也被称为热量平衡方程，即物体温度升高所需要的热量应与外界传入物体内部的热量及物体内部热源产生的热量之和相等。其中，第1项为单位时间内温度升高所需要的热量；第2、3、4项分别为外界由x、y、z方向传入物体内部的热量；第5项为物体内部单位体积产生的热量。

由于电缆多敷设于电缆沟或者隧道内，这两种敷设方式下的电缆暴露于空气中，根据边界条件给定了周围环境的温度以及物体表面与周围环境之间的对流换热系数，如式（2）所示。

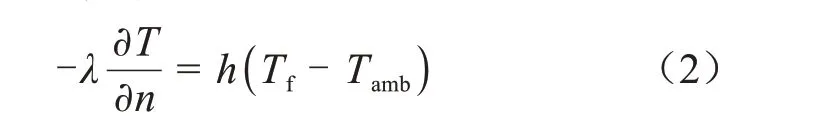
式(2)中：h为表面对流换热系数；Tf为发热体表面温度；Tamb为环境温度；λ为导热率；n表示方向。

仿真模型仅考虑外表面的空气自然对流，选取空气温度为20℃，对流换热系数为5 W/(m2·K)进行仿真。

电力电缆接头结构满足的热应力场问题分析也可以采用一系列张量形式的方程组进行描述，如式（3）所示。

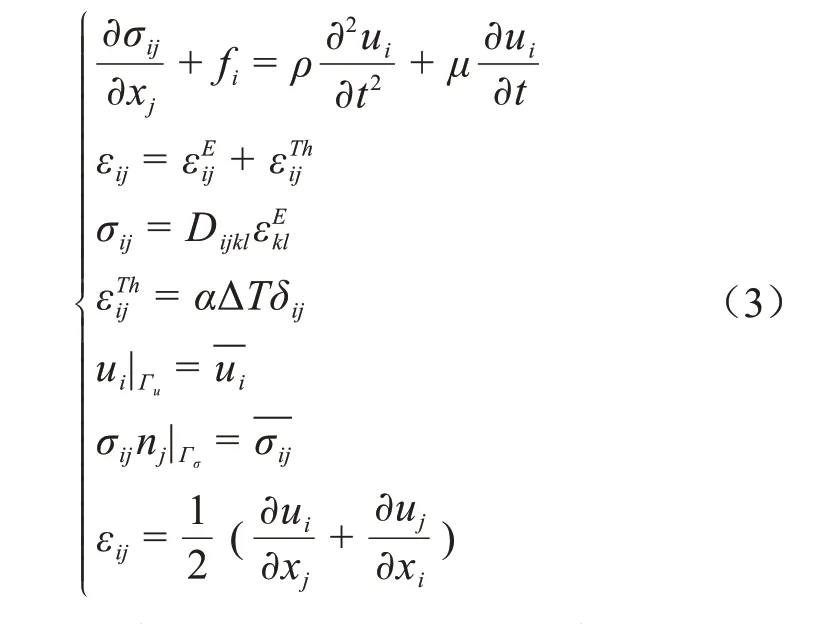
式（3）中：σ为应力张量；f为外部施加的力；ρ为材料密度；u为位移；t为时间；μ为阻尼系数；ε为应变张量；εE为弹性应变分量；εTh为热应变分量；D为应变系数；α为线膨胀系数；ΔT为与参考温度相比较的温度变化量；为边界上的位移值为边界上的应力值。另外，i=j=k=l=1,2,3。

其中，四阶张量D可通过式（4）确定。

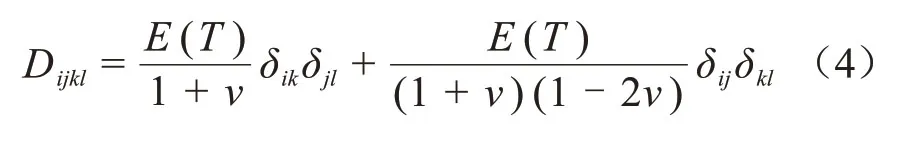
式（5）中：E(T)为材料的杨氏模量；v为材料的泊松比；δij为克拉克函数，其表达式如式（5）所示。

可推导得到应力表达式为式（6）。

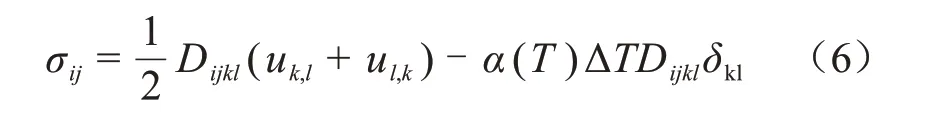
2 仿真结果与分析

2.1 水冷冷却方式对电缆熔融接头应力分布的影响

2.1.1 水冷温度的影响

构建的仿真模型的水冷界面见图1，仿真设置水冷的流体温度范围为283～302 K，水流速度为0.2 m/s，得到温度分布如图2所示。对比得到的不同温度分布图和等温线图，可以认为即使水冷温度不同，其冷却后的温度分布趋势基本相同，绝缘层距离水冷较近的地方温度较低，这是由于绝缘层在熔融接头内部，并且导热系数较小，不利于热量的消散。导线部分的温度基本一致，温度梯度较小，这是由于铜导线的导热性较好。经过1 h的水冷后，熔融接头整体基本降到室温附近，距离水冷部分较近的区域，温度偏低，考虑到水冷的水温较为接近室温，因此可以认为该熔融接头模型接近实际工艺情况。

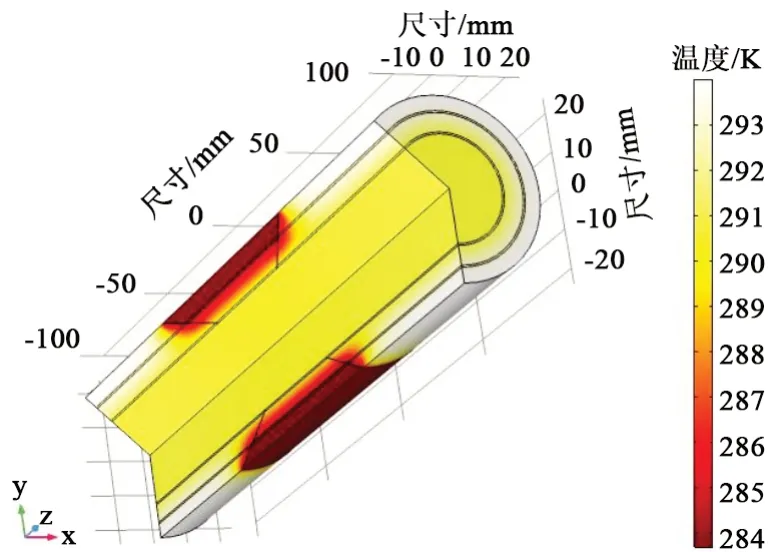
图2 水冷温度为283～302 K时熔融电缆接头三维温度分布Fig.2 Three-dimensional temperature distribution of cable fusion joint when the water cooling temperature is 283-302 K

图3 为水冷温度为286 K时绝缘层的应力分布图。从图3可以看出，在新、旧绝缘层的界面处的应力较大，并且靠近新交联的交联聚乙烯绝缘层界面处的应力更大。从沿新、旧交联聚乙烯界面的应力分布来看，沿界面向电缆外侧的应力更大。放大界面可以看到，沿界面靠近电缆内侧出现了比较严重的应力集中，这可能是因为水冷温度与交联聚乙烯绝缘层温差较大，所以在冷却过程形成此现象。

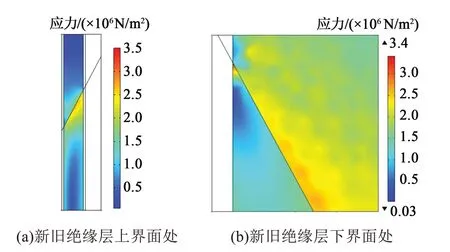
图3 水冷温度为286 K时的绝缘层应力分布图Fig.3 Stress distribution diagram of the insulating layer when the water cooling temperature is 286 K

当水冷温度上升时，整体的应力分布较之前没有太大变化，应力集中的现象依旧存在。选取界面附近的应力数据得到图4。从图4可以看出，随温度升高，不同温度的界面处应力分布趋势也有变化。不同温度下都是靠近电缆接头内侧的应力更大；水冷温度较低时，在距离内屏蔽层不到1.0 mm处达到极小值，之后又会随距内屏蔽层的距离增大而增大，并在约7.0 mm处达到极值，之后应力整体呈下降趋势；水温较高时，会在3.0 mm处出现极大值点，之后到8.0 mm处一直减小，随后呈整体增大的趋势。在0.5～2.0 mm应力随着水冷温度降低而减小，在3.0～9.0 mm随着水冷温度升高应力逐渐减小。沿界面方向看，水冷温度较低的应力波动更大。从应力最大值的角度来看，随水冷温度升高应力最大值逐渐升高，并且根据应力分布图可知应力最大值均出现在电缆最内侧。

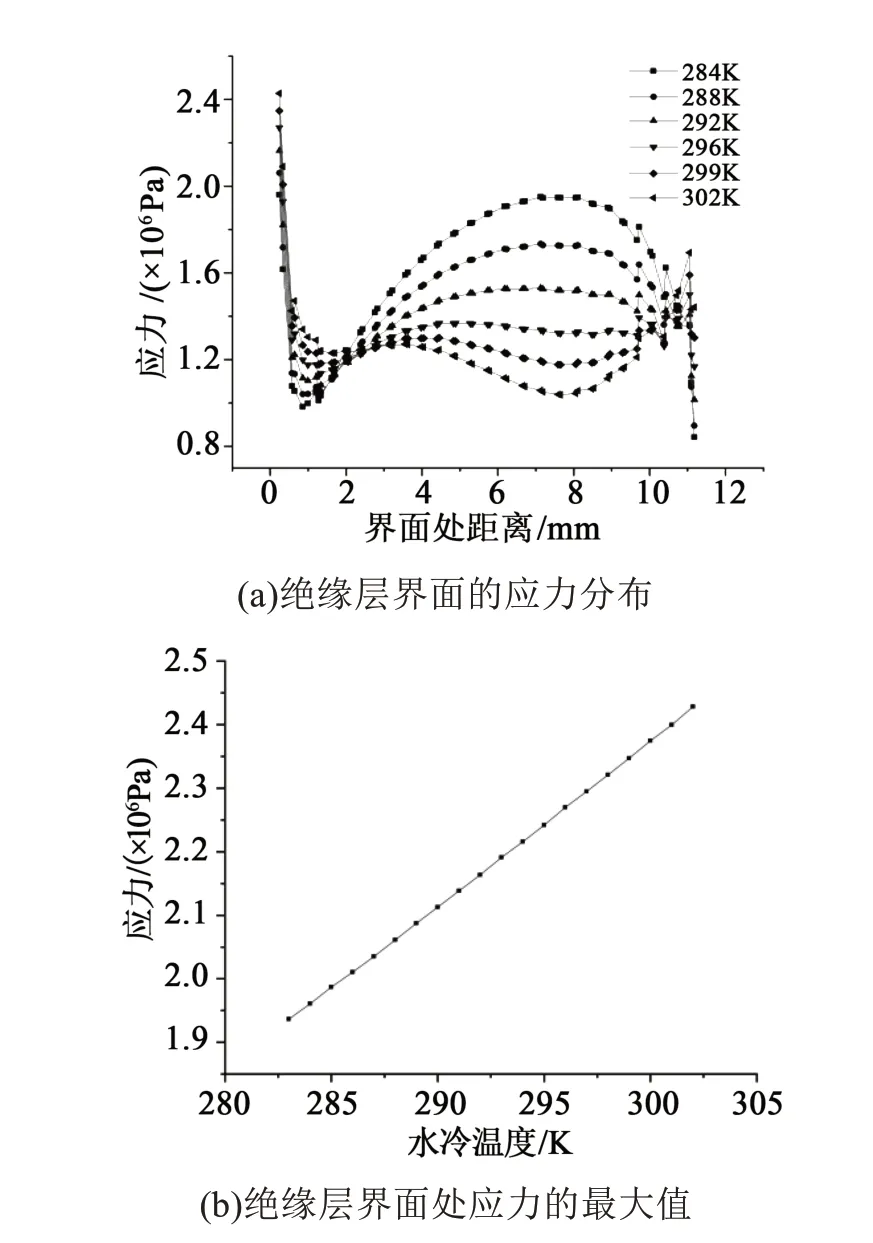
图4 不同水冷温度下沿绝缘层界面的应力分布及绝缘层界面的应力最大值Fig.4 The stress distribution along the insulating layer interface and the maximum stress at the insulating layer interface under different water cooling temperatures

2.1.2 水流速度的影响

电缆熔融接头水冷方式除了水冷温度可控，还有水流速度也可以改变，这些因素都可能会对电缆熔融接头的应力分布，尤其是界面处的应力产生影响。图5是不同水流速度下冷却30 min后绝缘层沿电缆接头径向的温度分布。从图5可以看出，流速较慢时，绝缘层沿电缆接头径向的温度要比流速较快时的更高，其中流速为0.2 m/s与0.4 m/s的温度差别最大，并且流速越大，流速差值对温度差异的影响越小。

图5 不同水流速度下冷却30 min后绝缘层沿电缆接头径向的温度分布Fig.5 The temperature distribution of the insulating layer along the radial direction of the cable joint under different water flow rates after cooling for 30 min

不同水流速度的应力分布同样存在上述的应力集中现象，在靠近内屏蔽层的新、旧绝缘层界面处存在较大应力。为了探究水流速度对绝缘层界面处应力的影响，将不同流速下界面附近的应力数据处理后得到图6和图7。从图6可以看出，不同水冷的水流速度下新、旧绝缘层界面处的应力大小基本相同，在约8 mm处的应力有不同，对比8 mm处不同流速下的应力，如图7所示。从图7可以看出，当流速较小时应力较小，随流速的增大应力的增量也逐渐减小，最后基本趋于定值。但即使是流速为0.2 m/s和2.0 m/s的应力差值也不过3%，可以认为流速对于水冷冷却的熔融接头模型的应力影响较小。

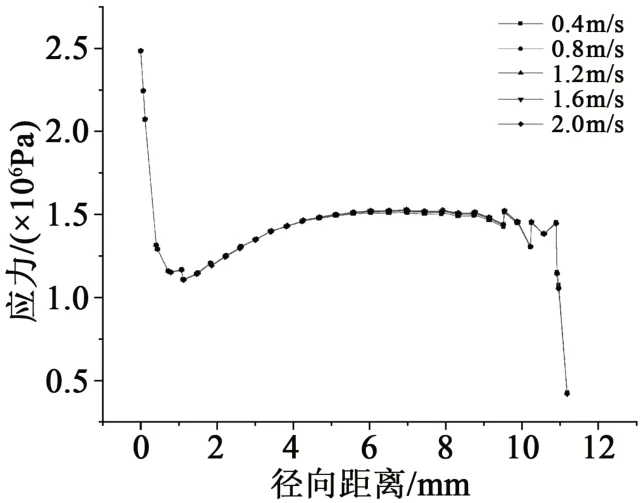
图6 不同水流速度下沿绝缘层界面的应力分布Fig.6 Stress distribution along the insulating layer interface under different water cooling flow rates

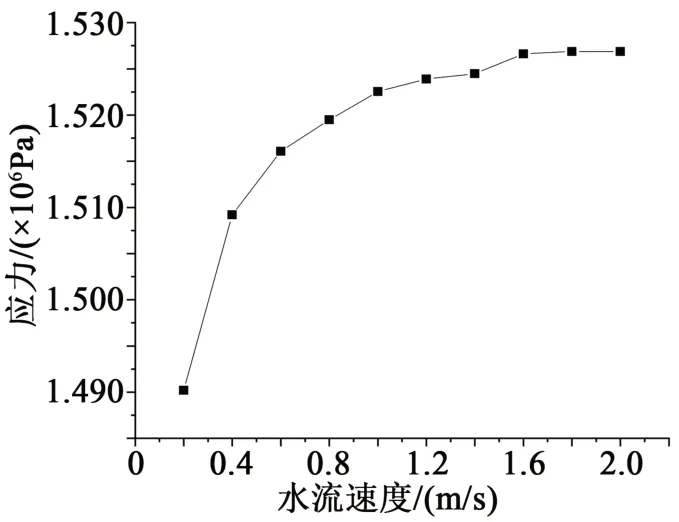
图7 不同水流速度下绝缘层界面的在8 mm处的应力Fig.7 The stress at the interface of the insulating layer at 8 mm under different water cooling flow rates

2.2 风冷冷却方式对电缆熔融接头应力分布的影响

除了水冷这种方式，电缆熔融接头同样会采用风冷方式，同一温度下风速越小冷却速度越慢，而实际的熔融接头制作要考虑时间成本的问题，风速较小不利于熔融接头的冷却，因此风速较小的温度分布及应力分布在此不做讨论。当风速为11 m/s时，冷却120 min后，熔融接头的整体温度接近室温。

关于熔融接头在风冷后的应力分布情况，基本与水冷的分布情况类似。将同水冷相同的几何位置的应力数据导出处理，得到不同风速下界面附近应力分布，如图8所示。

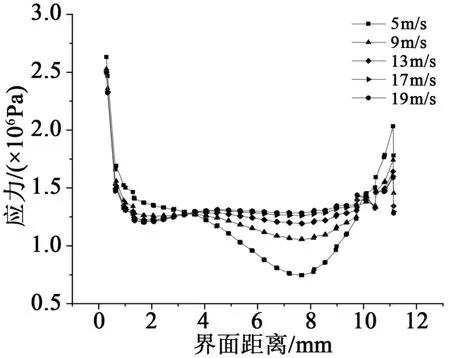
图8 不同风冷流速下沿绝缘层界面的应力分布Fig.8 Stress distribution along the insulating layer interface under different air-cooling flow rates

从图8可以看出，风速为5 m/s时界面附近的应力随着远离内屏蔽层而先减小后增大，在8 mm附近达到应力的最小值；随着风速的增加，沿着界面附近的应力分布趋势开始变化，当风速为19 m/s时，应力从屏蔽层到1.1 mm处逐渐减小，之后应力基本保持不变，说明除去绝缘层最靠近内侧的部分，冷却过程的降温一致性比较好。在7～20 m/s的风速冷却下，熔融接头的应力分布基本遵循应力随距离先减小后略微增大的规律，风速越大，在2～10 mm的应力波动越小。

因为不同风速下熔融接头新旧绝缘层界面的应力最大值都靠近内屏蔽层，所以将不同风速下的应力最大值提取出来比较，风冷温度为298 K，如图9所示。

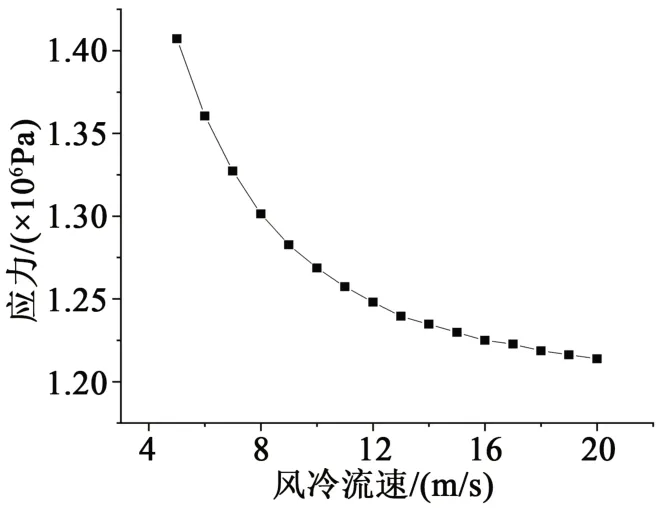
图9 不同风冷流速下绝缘层界面的应力峰值Fig.9 The peak stress of the insulating layer interface under different air-cooling flow rates

从图9可以看出，随着风速的增大，界面处的应力峰值逐渐减小，而减小的幅度随风速的提高而减小。这与水冷的界面处应力峰值随流速的趋势相反，但变化速率的情况相同，流速越大，应力峰值的变化速率越小。

除了风速对于界面附近应力的影响外，还有风冷的温度对应力的影响，图10是温度为283～298 K时，沿界面附近的应力分布。

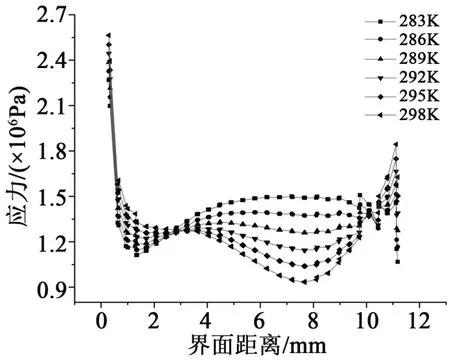
图10 不同风冷温度下沿绝缘层界面的应力分布Fig.10 Stress distribution along the insulating layer interface under different air-cooling temperature

从图10可以看出，不同风冷流速下沿界面应力的变化趋势基本相同，靠近内屏蔽的部分应力最大，绝缘层界面中间部分的应力则随着温度的升高而减小，这一点与水冷的情况相同。将应力峰值绘制成曲线如图11所示，从图11可以看出，应力峰值的变化随温度的升高基本呈线性变化，水冷方式亦然。

图11 不同风冷温度下绝缘层界面的应力峰值Fig.11 The peak stress of the insulating layer interface under different air-cooling temperature

2.3 不同材料差异对电缆熔融接头应力的影响

电缆熔融接头的制作涉及到熔接处新的交联聚乙烯绝缘层侧制作，新的绝缘层与旧的绝缘层存在材料性能不同的问题，旧的绝缘层存在老化问题。材料的性能差异可能导致界面处应力集中变化。通过改变旧绝缘层的材料热膨胀系数和杨氏模量与新绝缘层的差量，来研究其差异程度对应力分布的影响，结果如图12～13所示。

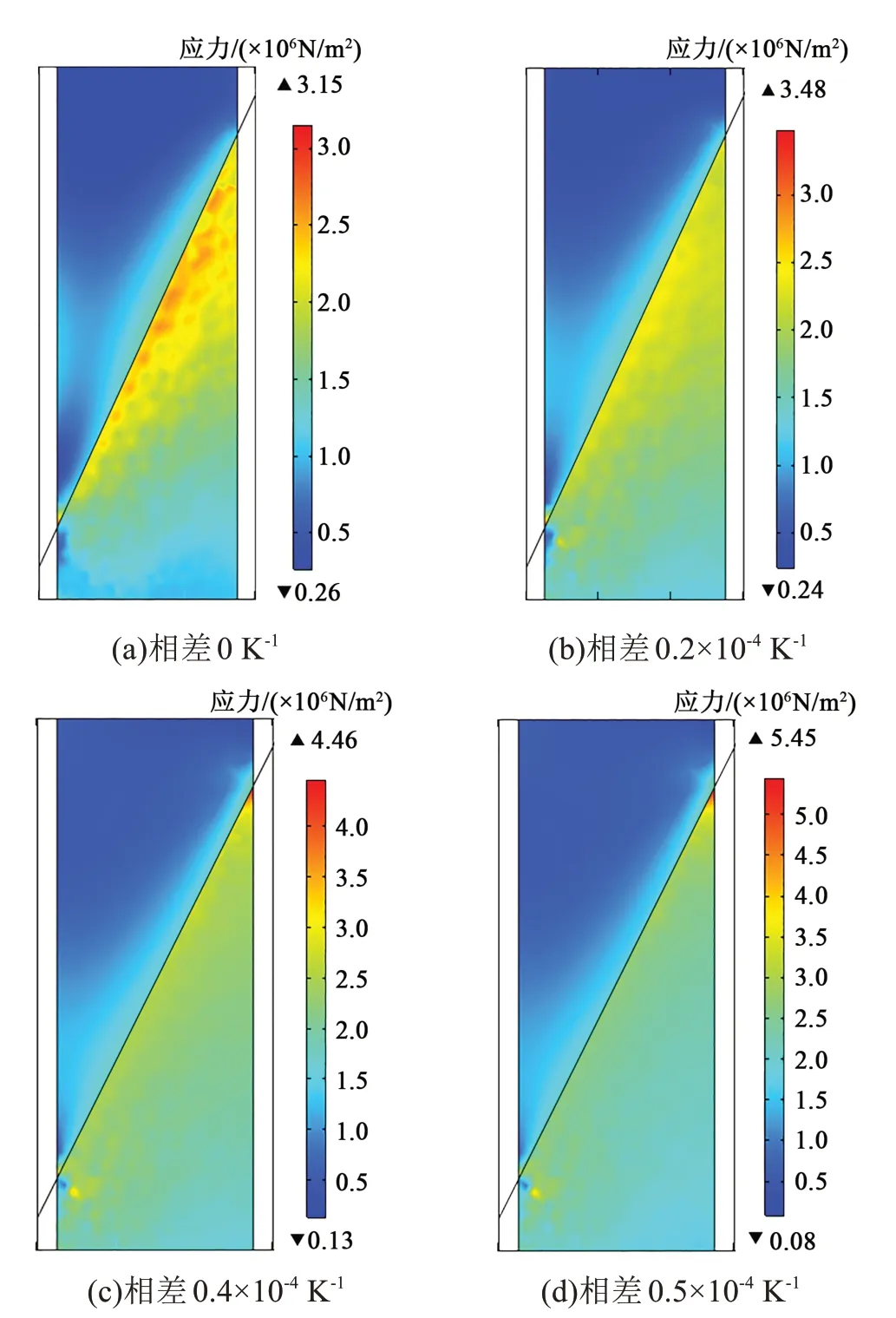
图12 不同新旧绝缘层材料热膨胀系数差异下应力分布Fig.12 Stress distribution under different coefficients of thermal expansion between new and old insulation materials

从图12可以看出，当热膨胀系数相差不大时，应力集中的部位位于内屏蔽处的界面附近，而随着热膨胀系数相差增大，外屏蔽层附近的界面处也产生应力集中的现象，应力集中位于新交联的绝缘层部分；当差异进一步增大时，靠近外屏蔽的应力集中现象更加严重，范围也更大。对比其应力最大值，随着热膨胀系数差值的增大，应力最大值也逐渐增大。

从图13可以看出，当杨氏模量差值较小时，沿界面的应力数值偏大，但内屏蔽层附近的应力集中现象依然存在。随着差值的增大，新绝缘层的应力开始减小；而应力极值随着材料杨氏模量的差值而增大，而且最大值位于应力集中点，意味着应力集中更加严重。

图13 不同新旧绝缘层材料杨氏模量差异下应力分布Fig.13 Stress distribution under the difference of Young's modulus between new and old insulation materials

因此针对上述现象，在制作熔融接头时，需要考虑到材料的适配问题，通过测量老化的绝缘层的相关材料参数，选取合适的新交联聚乙烯绝缘材料，这样可以在一定程度上减小应力，缓解应力集中现象。

2.4 不同冷却方式对电缆熔融接头应力的影响

熔融接头冷却过程采用水冷可以相对节约一定的时间，为进一步讨论不同水冷方式可能会对应力分布的影响，选用分段阶跃以及线性冷却的方式进行对比分析，结果如图14所示。从图14看出，直接采用分段阶跃冷却方式的应力要略高于线性冷却的方式，但两种方式的差别较小。说明水冷的方式确实会对界面处应力有影响，但影响有限。