冲击电压下35 kV预制式电缆终端的破坏机理研究

2022-10-21谢书凝孙铭张磊孙康张周胜

绝缘材料 2022年10期

谢书凝，孙铭，张磊，孙康，张周胜

（上海电力大学，上海 200090）

0 引言

根据电力电缆发生故障的数据统计，超过一半的电缆故障发生在电缆附件处[1-4]，电缆终端受电致应力作用时难免发生形变，引起绝缘层、半导电层体积变化，产生空气气隙，进而引发局部放电，导致终端破坏[5]。

高压电缆终端内部存在许多复合界面，容易在剥切处产生电应力集中现象，并且在现场安装过程中难以避免会接触到水分、灰尘等杂质，使得运行过程中存在潜在安全隐患[6-8]。由于缺陷的尺寸较小，难以在耐压试验过程中被检测发现，其破坏机制还有待研究。何金良等[9]指出电缆终端等部位由于电场分布不均匀，承受电场强度远大于整体电场强度平均值，导致发生电晕、局部放电等现象，进而使电介质材料老化速度加快，老化程度加剧，威胁电力系统安全；高寒等[10]建立320 kV高压直流电缆终端模型进行仿真分析，研究发现在直流叠加冲击电压作用下，界面切向场强在绝缘屏蔽层搭接位置出现畸变，最大场强位于屏蔽层顶部，交联聚乙烯绝缘屏蔽层为终端内部薄弱位置；刘昌等[11]研究表明硅橡胶附件承受较大机械应力时，环向机械应力增加，极端情况下使绝缘介质内部发生破坏，导致击穿；承受较小机械应力时，预制件与绝缘表面界面压力过小，于界面处产生微小气隙等缺陷，导致界面放电；康文斌等[12]采用工频叠加谐波电压对电缆终端进行加压试验，结果表明随时间延长，电子和空穴陷阱能级变浅，导致载流子迁移率增大，电导率上升，当电导率上升到一定值时，绝缘电介质将失去绝缘性能，导致绝缘失效，介质损耗因数随频率下降而呈现逆幂函数增大趋势；A TZIMAS等[13]对长期受电、热应力绝缘材料的耐久性能进行研究，结果表明电应力对电缆的耐久性能影响小于热应力，电、热应力共同作用将导致电缆寿命降低，显著老化。杨鑫等[14]分析220 kV电缆接头电磁-热-应力耦合的作用机制，得出复合材料界面电场、温度场、应力场均发生二次畸变，热应力畸变最明显，对高压电缆接头故障发展起始阶段起重要作用。万子逸等[15]针对高频截波下电缆终端电-热场特性进行研究，发现半导电层截断处附近热功率损耗最大，易形成局部热点，且谐波电压升高比谐波频率升高带来的影响更为显著。

电缆终端在冲击电压作用下材料的介电特性与在工频/直流电压下不同，电、热、机械应力均增大，会危害电力系统运行安全。因此，本文建立35 kV预制式电缆终端模型，研究冲击电压下电缆终端材料的介电特性，分析频率对电场分布和机械应力的影响以及热效应，探讨电缆终端在冲击电压作用下的破坏机理。

1 仿真

1.1 冲击电压

冲击电压一般用非周期性双指数波表示，如式（1）所示[16-18]。

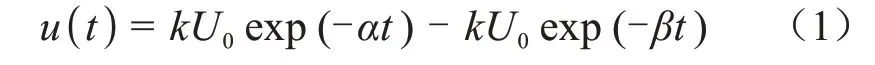
式（1）中：k为波形校正系数，本文取k=1.04；U0为冲击电压峰值，根据GB/T 12706—2020中35 kV预制式电缆终端冲击电压试验峰值，本文U0取值为200 kV[19]；α、β分别为波头衰减系数及波尾衰减系数，其中α=0.014，β=2.5。

图1为冲击电压频谱，冲击电压通过傅里叶变换可以分解为直流分量和k个谐波分量。

图1 冲击电压频谱Fig.1 Impulse voltage spectrum

1.2 仿真模型及参数设置

图2 为35 kV预制式电缆终端模型，由于高压电力电缆终端具有对称性，为简化仿真计算，模型构建为电缆终端的一半。采用有限元仿真，在电缆终端外部设置矩形边界框，设置矩形为零电荷，填充介质为空气，将外护套及屏蔽层接地。

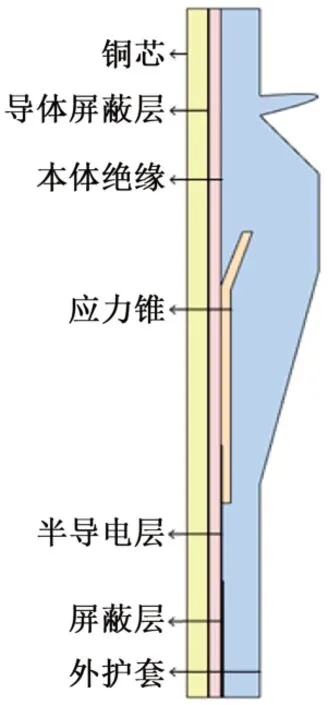
图2 电缆终端模型Fig.2 Cable terminal model

表1所示为在室温293.15 K下电缆终端各结构材料的相对介电常数ε及电导率γ取值。半导电层及导体屏蔽层的电导率远大于本体绝缘电导率，由于频率对半导电层及导体屏蔽层的复介电常数的虚部影响较大[20]，本文主要分析半导电层介电常数的高频特性，认为本体绝缘的介电常数不随频率变化。

表1 电缆终端各部分材料参数Tab.1 Material parameters for each part of the cable terminal

2 电缆终端应力分析

2.1 电缆终端电应力分析

图3(a)为冲击电压达到峰值（U0=200 kV）时的电缆终端电场分布。从图3(a)可知，电缆终端电场强度最大值为133.911 kV/m，位于半导电层与应力锥相交点处，图3(b)为图3(a)中方框即半导电层应力锥交界处电场分布，应力锥内部电场由左至右递减。图4是冲压电压下电缆终端本体绝缘、半导电层及屏蔽层的电场强度曲线，由图4可知，此时本体绝缘电场强度为13.33 kV/m，半导电层处的电场强度为28.85 kV/m。

图3 冲击电压峰值时刻半导电层应力锥交界处电场Fig.3 Electric field at junction of semi-conductive layer at peak time of impact voltage

采用式（2）所示双指数形式表示图4中的时域变化规律。

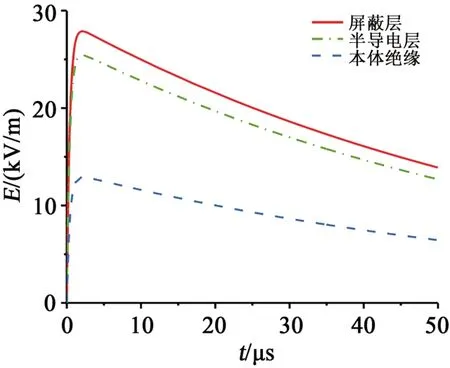
图4 本体绝缘、半导电层及屏蔽层电场强度Fig.4 Electric field strength of the body insulating layer,semi-conductive layer and shielding layer

对半导电层曲线进行拟合可得a=26401，b=26387，c=0.015，d=2.464，用于函数傅里叶分解。

冲击电压中高频信号作用引起介电常数的变化，会导致电场分布存在一定偏差。为研究不同谐波分量作用对电缆终端电场分布的影响，本文采用复介电响应模型[21]表征介电常数的频率特性，如式（3）～（5）所示。

式（3）～（5）中：ε*为复介电常数；ε′为复介电常数实部；ε′′为复介电常数虚部；tanδ为介质损耗因数；γ为电导率；fk为不同谐波分量对应频率，其中k=1,2,3,…，本文选取1～10次谐波分量。

表2为1～10次谐波电压下电缆终端本体绝缘、半导电层以及屏蔽层的电场强度。从表2可以看出，屏蔽层处电场强度稍大于半导电层电场强度，本体绝缘处电场强度较小，随谐波次数增加，相邻谐波电场强度差均减小。

表2 1～10次谐波作用下本体绝缘、半导电层及屏蔽层电场强度Tab.2 Electric field strength of body insulation,semi-conductive layer and shielding layer under 1-10 harmonic action

将半导电层电场强度表达式（2）由时域变换至频域，并取1～10次谐波分量如表3中的E2。变化率α表达式如式（6）所示。

式（6）中：E1为直接施加雷电冲击电压时半导电层电场强度谐波分量；E2为考虑半导电层介电常数频率特性的电场强度。

从表3可以看出，α≥0，即考虑频率对介电常数影响后，对应频率的半导电层电场强度变小。高频信号对介电常数的影响会使得电场强度更加均匀，减小最大畸变电场。因此，冲击电压中的高频信号引起电场强度变化不是造成电缆终端破坏的主要原因，反之，起到均匀电场的作用。

表3 不同方法下半导电层谐波分量Tab.3 Harmonic components of the semi-conductive layer in different methods

为进一步研究电缆终端不同交界面处电场分布，选取导体屏蔽层与本体绝缘交界即截线1，半导电层与本体绝缘交界即截线2，半导电层与屏蔽层交界为截线3，截线5位于应力锥底部，与截线5上、下间距0.5 mm分别为截线4和6，如图5所示，当仅1次谐波单独作用时，不同截线处电场的电场分布如图6所示。

图5 截线位置Fig.5 Crossing line position

图6 不同截线位置电场分布Fig.6 Distribution of electric fields of section line at n=1

从图6可以看出，截线2处电场强度在半导电层与应力锥相交处附近增大并在应力锥底部发生畸变，半导电层与应力锥重叠部分电场强度不断减小但减小速度较为缓慢，这是由于应力锥的存在，改善电应力集中现象[22-23]，起到了均匀电场的作用。截线1电场强度在屏蔽层顶端附近缓慢增大，在应力锥交界处附近减小，而后由于尖端电场畸变的影响，电场强度增大。截线4、5、6均在应力锥与半导电层相交处发生畸变，畸变发生后，由于应力锥的存在，均匀了电缆终端半导电层的电场分布，使半导电层边界电场强度降低，因此截线4电场强度快速减小，且大于截线6电场强度。

2.2 电缆终端的热应力分析

电缆运行过程中难以避免发生损耗，为分析冲击电压对电缆终端的影响，在静电模块基础上添加固体传热模块进行热仿真。本文设置电缆终端温度初始值为室温293.15 K，空气对流热通量为8 W/(m2·K)，铜芯处损耗如式（7）所示[24]。

式（7）中：u(t)为冲击电压；R为铜芯电阻。

冲击电压作用下电缆终端在截线4、5、6处的温度变化及温度梯度变化如图7所示。

图7 截线4、5、6温度及温度梯度分布Fig.7 Distribution of temperature and temperature gradient of section line 4,5,and 6

从图7可以看出，在冲击电压作用下，截线处整体温度变化较小，电缆终端温度最大值为297.25 K，位于铜芯内部，基本接近初始温度，但铜芯处温度分布较为均匀，冲击电压引起的温升基本可以忽略。这可能是由于单次冲击电压作用时间极短，能量转换为温度变化的过程较为缓慢，无法在短时间内体现。

温度梯度曲线中的两个波峰位置分别位于铜芯与导体屏蔽层交界处、导体屏蔽层与本体绝缘交界处。导体屏蔽层使终端内部的热量增加[25]，热场畸变较为严重，由于应力锥的存在改善了终端内部的电应力集中现象[26]，温度梯度两处波峰均出现在应力锥下方截线6处。截线6导体屏蔽层区域处温度由295.63 K降至293.41 K，由于热量由铜芯向外护套方向递减，温度梯度最大值位于铜芯与导体屏蔽层交界处，为18618.51 K/m，导体屏蔽层内部随着电场强度的增大温度有所升高，但温度变化较小，在本体绝缘交界处存在较小幅度的波峰。

2.3 电缆终端的机械应力分析

电缆终端内部的半导电层在应力锥、屏蔽层以及本体绝缘的约束下，由于电场作用产生电致应力会发生微小形变，如图8所示应变u在半导电层与铜屏蔽层、应力锥交界外分解为两个互相正交的径向分量u1及轴向分量u2。

图8 体积应变分解图Fig.8 Volume-strain decomposition diagram

受频率作用影响，半导电层复介电常数虚部变化较大，而电致伸缩系数与复介电常数息息相关，由表1可知本体绝缘及应力锥电导率极小，接近于0，根据公式（5）认为其介电常数虚部不随频率改变，进而其电致伸缩系数不随频率变化而改变，因此本文仅对半导电层处电致伸缩系数进行计算。在高频分量作用下，半导电层复介电常数随频率增大快速减小，其电致伸缩系数随之改变，介电电致伸缩系数可用来表示电致应力与介电常数之间的关系[27-28]，如式（8）～（10）所示。

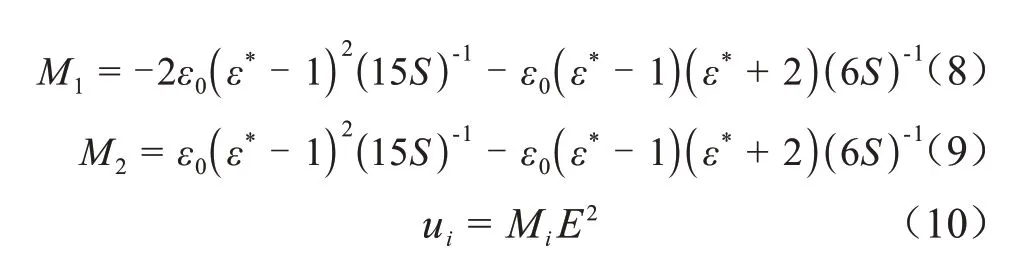
式（8）～（10）中：M1为介电电致伸缩系数轴向分量；M2为介电电致伸缩系数径向分量；S为杨氏模量，本文取190 GPa；ε0为空气介电常数；ε*为复介电常数；i=1,2。

取1～10次谐波分量的应力系数分析，如表4所示。从表4可以看出，介电电致伸缩径向系数基本为轴向系数的3倍，且随谐波次数增加，应力系数逐渐减小。

表4 不同谐波分量应力系数Tab.4 Stress coefficient of different harmonic components

一次谐波单独作用时，图6(a)截线2处最大畸变处电场为43.697 kV/m，图6(b)截线5处最大畸变处电场为120.022 kV/m，结合表4中介电电致伸缩系数，由式（10）可得，截线2对应轴向应变为1.13%。截线5对应径向应变为2.54%。

由应变定义可求得半导电层尺寸变化[29]，如式（11）所示。

式（11）中：L为应变前初始长度；ΔL为应变变化长度。

半导电层长度为355 mm，宽度为0.5 mm，对应的尺寸变化分别是轴向压缩4.01 mm，径向压缩0.013 mm间隙，半导电层与应力锥相交点处径向应变大于截线2处轴向应变，导致半导电层发生收缩，半导电层和绝缘之间容易出现间隙，是导致终端破坏的主要起始原因。

综上研究，冲击电压会导致半导电层介电性能改变，从而对电缆终端电场及热场分布产生影响，但电缆终端电场强度在谐波分量作用下改变较小，最大变化率仅为0.072%，冲击电压下电缆终端温度最大值为297.25 K，最小值为293.41 K，整体温度变化在5 K以内，基本与初始温度相同，其温升可忽略不计，因此电、热应力并非造成电缆终端破坏的主要原因。进一步计算分析冲击电压下半导电层交界处的电致伸缩系数，发现介电电致伸缩径向系数基本为轴向系数的3倍，一次谐波单独作用时最大径向应变为2.54%，造成径向压缩0.013 mm，容易产生间隙，导致电缆终端破坏，综合分析得出冲击电压作用下电场强度及温度变化不明显，并非造成电缆终端破坏的主要原因，电缆终端半导电层与铜屏蔽层、应力锥交界处在电致应力作用下收缩容易产生气隙，最终可能导致击穿。