计及多能设备变工况运行特性的综合能源系统日前优化调度

董文杰，田志强，姚玉斌，隋向阳，李俊格，曾顺奇

（1.东方电子股份有限公司，山东 烟台 264000；2.大连海事大学 船舶电气工程学院，辽宁 大连116026；3.广东省电网公司 广州供电局，广东 广州 510620）

0 引言

随着能源危机、环境污染以及气候变化等全球性挑战的日益严峻，传统能源供应体系存在的能源利用效率不高、互补替代性较差、清洁化程度较低等弊端逐渐凸显。综合能源系统（Integrated Energy System，IES）融合了多项能源生产、传输、转换、利用新技术的能源供应新形式[1]～[3]，其通过能源耦合设备将电气冷热等多种形式能量流相互耦合，充分发挥不同品位能源之间的梯次利用与耦合互补潜力，从而提升能源综合利用效率、降低污染物和CO2排放、提高系统运行经济性，并为可 再 生 能 源 消 纳 提 供 新 途 径[4]，[5]。

综合能源系统优化调度是实现多个主体互补互济、协同运行的重要手段之一，设备模型则是系统优化调度的关键基础。长期以来，优化调度领域的研究更加关注调度体系的构建、调度方法的鲁棒性以及优化调度模型的求解算法，对系统中各类设备的数学模型做了较大简化。文献[6]提出了基于能量集线器（Energy Hub）的综合能源系统优化调度架构，其中大部分设备采用了简单的输入-输出效率模型，即设备的输出等于其输入乘以一个恒定的效率系数。该模型简单实用，在优化调度模型的约束集中，仅会增加部分线性等式约束，不会显著增大优化模型的求解难度。但是该近似模型的适用范围有限，仅能在一定的负载率范围内对部分输入-输出特性近似为线性的设备实现较小误差近似。在实际运行中，系统可再生能源出力和多能负荷会随时间变化，因而设备也往往处于变工况运行状态。对于变工况运行特性复杂的部分设备，此模型可能导致近似误差较大。文献[7]研究了包括微燃机发电机组、蓄电池、电制冷机和吸收式制冷机的部分负荷运行模型，并对比了其与常系数效率模型对于调度结果的影响，指出两种模型对于调度结果的误差影响不可忽略，并且前者可以获得更为准确的调度结果。文献[8]研究了设备变工况运行特性模型，对于综合能源系统优化设计与运行的影响，并给出了减小常系数效率模型的实用策略。在设备级变工况运行特性建模方面，文献[9]在分析典型元件性能的基础上，建立了定转速单轴燃气轮机部分负荷特性的显式解析表达式。文献[10]，[11]从机理和数据建模等角度分别研究了不同容量热电联产机组的变工况运行特性。文献[12]基于实测运行数据拟合了内燃机及其热电联产系统的典型变工况特性曲线。文献[13]从机理分析角度出发，将变工况运行中的换热系数看做常数，并由此得到了余热锅炉变工况模型的解析形式。文献[14]分别研究了热泵空调机组的变工况性能，并开发了相应的测试平台。在计及设备变工况运行特性的系统优化方面，文献[15]在考虑内燃发电机组和吸收式制冷机组变负荷特性的基础上，建立了系统经济运行模型；随后利用TRNSYS优化该模型，并封装至Matlab；最后通过遗传算法实现非线性规划问题的求解。文献[16]基于燃气轮机、余热锅炉、吸收式制冷机和电制冷机等设备详细的变工况运行特性，建立了综合能源站的最优容量规划两阶段模型，并应用群搜索算法和数学规划方法分别对两阶段优化问题进行求解。文献[17]建立了一种动态能量路由器模型对多能设备的运行效率进行修正；由此建立了计及设备变工况特性的区域综合能源系统优化调度模型；通过AIMMS软件进行求解。文献[18]针对计及设备变工况运行特性的系统优化规划模型，采用广义Benders分解将原问题分解为设备容量配置主问题和设备功率分配子问题，并分别利用CPLEX和动态规划算法对各子问题进行求解。

针对计及设备变工况运行特性的非线性优化模型，尚无稳定通用的求解算法和商业求解软件，基于启发式算法的求解策略尽管在一些场合可以求得问题的可行解，但存在全局搜索能力较弱、容易陷入局部最优解和初值依赖度高等不足之处。本文将增量线性化策略[19]应用于此类优化问题的求解中，通过选取合适的分段点，并在各分段上引入0～1变量，将非线性的设备变工况运行特性约束转化为一系列线性的等式和不等式约束，从而将原问题转化为一个混合整数线性规划（Mixed Integer Linear Programming，MILP）问 题，通 过 调 用成熟的商用求解器（如CPLEX，GUROBI等）实现快速求解。本文还提出了一种基于误差控制的分段点选取方法，通过构造偏差函数并控制其极值范围，可以将最优解的误差水平限制在给定的水平内。

1 多能设备变工况运行模型

在综合能源型系统优化调度领域，已有部分研究采用多能设备恒定效率模型，即通过恒定的效率系数来刻画设备的输入-输出特性。图1给出了综合能源系统中3种典型设备的运行特性[18]。

图1 3种典型设备的变工况运行特性Fig.1 Off-design operation characteristics of 3typical facilities

当设备偏离额定运行点时，效率系数、耗量特性等运行特性可能会随之改变，此时设备处于变工况运行状态。将能够描述该状态下设备运行特性的数学表达定义为该设备的变工况-变负荷运行模型。在优化调度场景中，一般地，设备的变工况运行模型，可以通过对该设备的运行机理分析和实测数据分段拟合获得，并表示成分段拟合函数为

式 中：x，y分 别 为 该 设 备 的 输 出 量 和 输 入 量；fi（x）为第i个分段上的拟合函数；N为自变量x的所有分段数；，分别为各分段上自变量x的下限、上限。

为了便于应用，可用多项式函数或分段多项式函数拟合设备的变工况运行特性[18]，即：

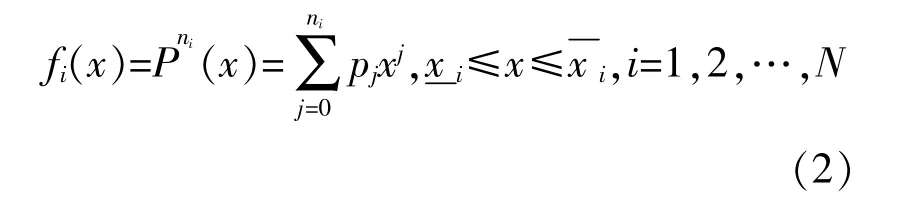
式中：ni为第i个分段所对应的多项式拟合函数的最高次幂。

多项式函数的拟合误差主要取决于多项式的幂次和分段数，适当地调整拟合函数的幂次并增加分段数，可将拟合误差限制在给定范围内，满足工程应用的精度需求。该方法适用于绝大部分电力和热工设备。当拟合函数有多个自变量时，多项式拟合函数会具有较为复杂的数学形式，不利于后续应用于优化调度中，因此该方法对于单自变量非线性函数的使用效果较好，而在近似多自变量的运行特性函数时，则有一定局限性。

2 综合能源系统日前优化调度模型

2.1 目标函数

综合能源系统日前优化调度的目标可以关注经济性、能效性和环保性等多个指标维度。本文仅以最常见的日前经济调度为例，介绍系统优化模型的建立和求解过程。日前，经济调度的目标函数为最小化系统下一日总运行费用，即：

各项费用的计算方法为

式中：Sg为燃气设备所构成的集合，包括燃气轮机、燃气锅炉等；Se为用电设备所构成的集合，包括电锅炉、电压缩式热泵、电制冷机等；Sp为弃风/光设备所构成的集合，包括风电场、光伏电站等；为t时刻设备i的单位弃风/光功率惩罚费用；为t时刻设备i的弃风/光功率；Sm为有运行维护费用设备所构成的集合，包括燃气轮机、电制冷机等需要定期维护的设备；t时刻设备i的单位功率运行维护费用；t时刻设备i的出力功率；为t时刻系统向电网售电的单价；为t时刻系统向电网售电的功率。

2.2 约束条件

日前优化调度模型的约束条件包含两个部分：母线功率平衡约束和设备运行约束。其中，母线功率平衡约束包含电母线、热母线和燃气母线功率平衡约束分别为

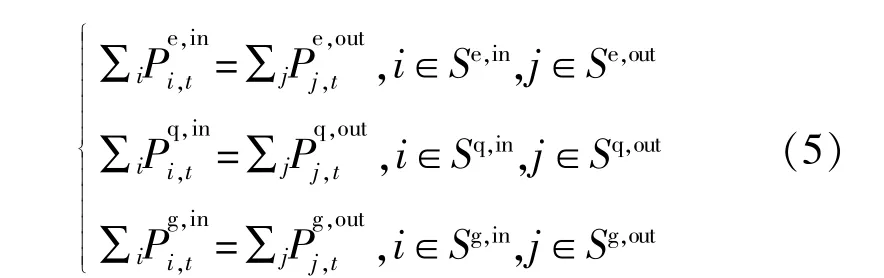
由于本文的研究对象是较小规模的区域级综合能源系统，负荷容量通常小于数百kW，并且电/气/热网络拓扑简单、规模小，网络传输特性对于调度结果的影响较小，因此未考虑复杂的电网和热网传输约束。

设备运行约束包括描述输入-输出特性的变工况运行模型[式（2）]和设备输出功率上下限、爬坡约束，即：

对于储能设备，还应满足：

式 中：Et0，Et，Etend分 别 为 初 始 时 刻、t时 刻 和 末 尾 时刻储能设备的蓄能量；和，分别为t时刻的蓄能功率和放能功率；ηc，ηdisc分别为t时刻的蓄能效率和放能效率；γc，γdisc分别为t时刻的蓄能状态标记量和放能状态标记量；γc，γdisc取1时表示设备处于蓄能、放能状态，取0时表示未处于蓄能、放能状态；Pc，Pdisc分别为设备的最大蓄能功率和最大放能功率。

3 优化模型求解

在计及设备变工况运行特性的综合能源系统日前优化调度模型中：决策变量包含连续型变量与0～1变量；目标函数中可能含有非线性项；约束条件中也含有非线性的设备变工况运行特性约束。该优化模型可以归结为一个混合整数非线性规划问题，目前尚无成熟的商用求解器可以实现高效求解。

针对上述模型，本节采取的整体求解思路：先将目标函数和约束条件中非线性项进行线性化处理；由此将原问题转化为混合整数线性规划问题；进而通过调用成熟的商用求解器（如CPLEX，GUROBI等）进行求解。

3.1 增量线性化处理策略

对于目标函数中的非线性部分，记其形式为miny=C（x），可以通过增量线性化策略将其转化为[19]

式中：N为总的分段数；ak为自变量在第k个分段上 的 位 置，其 取 值 为[0，1]。除 式（8）外，还 须 要 将以下等式约束并入日前优化调度模型的约束集中：

式中：bk为自变量在第k个分段上的状态标记符，其取值为0或1。当自变量的取值未覆盖第k个分段或未落在第k个分段上时，bk取0，否则取1。对于约束条件中的非线性部分，不妨假设其为分段非线性拟合函数，可由式（1）表示。可通过同样的增量线性化策略将其转化为

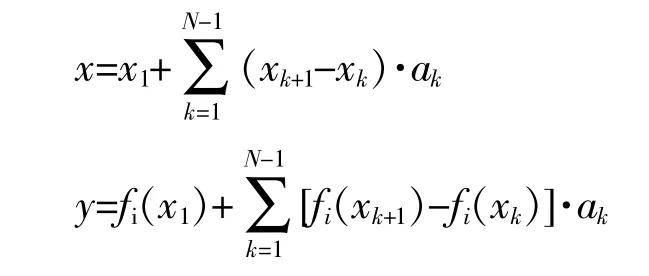
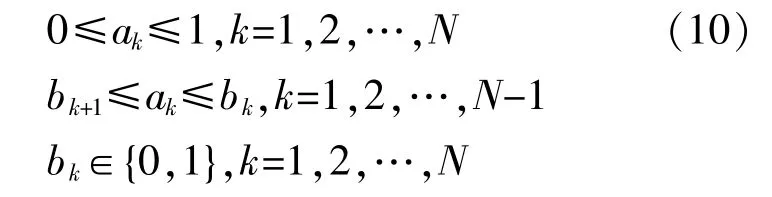
只要将日前优化调度模型中：①目标函数中的非线性部分用式（8）替换，并在约束条件中加入式（9）约束；②约束条件中的非线性部分用式（10）替换，即可得到线性化的调度模型，该线性化方法的原理如图2所示。

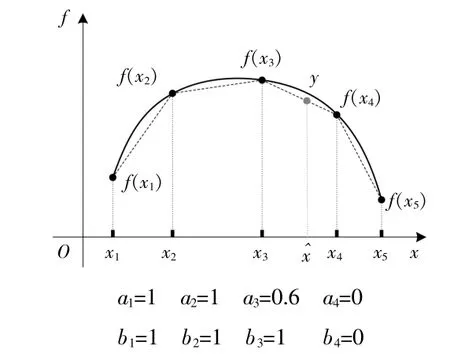
图2 增量线性化方法Fig.2 Schematic diagram of the incremental linearization method

3.2 基于误差控制的分段点选取方法

现有文献关于增量线性化过程中分段点和分段数的选择鲜有涉及，大多通过工程经验进行选取。事实上，分段点的选取应当权衡非线性模型的线性化精度和优化模型的求解时长，因为较多的分段点通常可以获得较高的线性化精度，但也会引入更多的0～1变量和约束条件，从而增加优化模型的求解时间。考虑到日前优化调度场景通常对于计算实时性的要求不高，具有较为宽裕的模型求解时间，因此本节不考虑求解时长对于分段点选取的影响，仅从线性化误差控制的角度探索分段点选取方法。该方法的基本原理如图3所示。

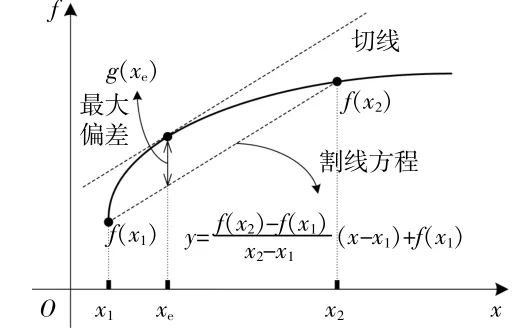
图3 分段点选取方法示意图Fig.3 Schematic diagram of the segmentation point selection method

本文目标是在给定的误差水平 εr下确定分段 点x2，x3，L，xN-1的 具 体 位 置。以 分 段 点x2的 确 定为例，该方法包含以下具体步骤。

①确定分段[x1，x2]上的割线方程：

②构造原函数与其线性化函数之间的偏差函数：

③通过式 （13）求取偏差函数的所有极值点xe，i，i=1，2，…，Ne：

式中：Ne为偏差函数极值点的总个数。

④根据给定的误差水平 εr及式（14）确定分段 点x2，i，i=1，2，…，Ne：

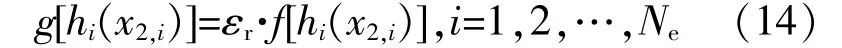
需要说明的是，误差水平 εr为偏差量与原函数值的比值，是相对误差概念。

⑤将 第④步 求 得 的 分 段 点x2，i，i=1，2，…，Ne代 入 偏 差 函 数g（x），由 于g（x）可 能 存 在 多 个 极 值点，并且须要将偏差函数的最大值限制在给定范围内，因此取令达到最大值时的分段点作为最终的x2，即：便得到了线性化近似误差恰好为 εr的分段点，对于任意分 段[xk，xk+1]，只 要 令xk=x1，xk+1=x2，重 复 上 述 步 骤即可得到分段点xk+1的取值。需要说明的是，如计算得到的分段点大于自变量的右边界，即xk+1＞x¯，则表示xk+1为最后一个分段点，并应令xk+1=x¯。

在实际工程中，由于拟合精度和计算复杂度适中，三次多项式函数通常被用来拟合设备的变工况运行特性[20]。

4 算例分析

4.1 系统配置

本文算例系统如图4所示。该系统与上级电网相连，但只从电网购电，不向电网售电；盈余的风电可以弃掉，弃风有惩罚成本；风机、上级电网和联产机组共同为电负荷和电锅炉提供电能；联产机组、电锅炉和燃气锅炉为系统热源，共同满足热负荷需求；燃气源同时为联产机组、燃气锅炉和燃气负荷供应燃气。系统的优化目标为日运行费用最低，包括从气源购气费用、从电网购电费用和弃风惩罚费用。

图4 算例系统结构Fig.4 Structure of the case system

系统电、热、燃气负荷预测值以及风电出力预测值和分时电价及购气成本如图5所示。

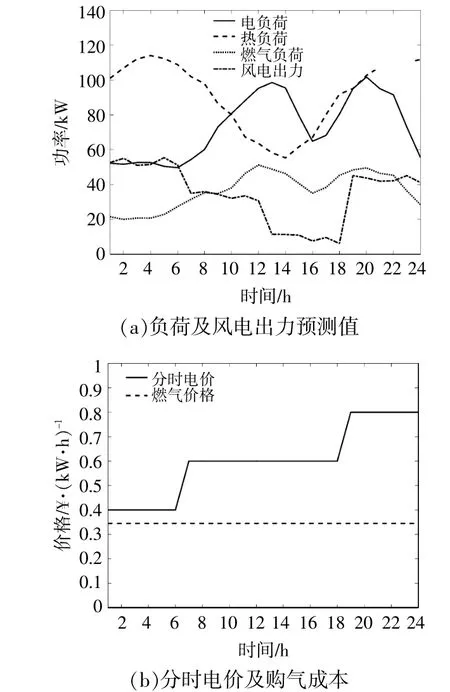
图5 算例系统部分参数图Fig.5 Some parameters of the case system

考虑燃气热电联产机组的变工况运行特性，其燃气耗量特性和热功率出力特性均可近似表示为输出电功率的三次多项式函数，系统所有设备参数、负荷波动、风电出力和价格数据见文献[20]。经线性化处理后的优化调度模型通过MATLAB的YALMIP工具箱调用CPLEX求解器进行求解，各设备的调度间隔为1h。

取线性化允许的相对误差水平为5%，通过前文所提的基于误差控制的分段点选取方法，可以确定联产机组燃气耗量特性和热功率出力特性函数的分段数和分段点具体位置，如表1所示。

表1 联产机组变工况运行特性的分段线性化参数Table1 Piecewise linearization parameters for off-design characteristics of the cogeneration unit

4.2 仿真结果

算例系统的日前优化调度模型为一个典型的混合整数线性规划问题，其中0～1变量由非线性的设备变工况运行特性约束,经分段线性化处理而引入。该问题可由CPLEX求解器内置的分支定界法结合内点法求解，电功率的最优调度结果如图6所示。

图6 电功率调度结果Fig.6 Dispatch results of electric power

在1：00-9：00，风电出力处于较高水平而系统电负荷处于较低水平，因此联产机组通过压低其电功率出力来为风电消纳提供更多空间。由于此时热负荷处于较高水平，联产机组的热功率出力也须要保持在相对高的水平上，这在一定程度上钳制了其电功率出力，即联产机组的电功率出力也不能太低。与此同时，电锅炉大幅增加出力，通过消纳便宜的风电来提升系统运行经济性。当电 负 荷 迎 来 第 一 个 尖 峰 时（10：00-16：00），由 于热负荷处于较低水平，联产机组的热、电出力均被钳制在较低水平。此时风电出力也较少，系统面临电功率供应短缺情况，于是增加从电网购电来抵消电功率缺额。当电负荷迎来第二个尖峰时（17：00-22：00），热负荷恰好也处于较高水平，此时联产机组电出力按满负荷运行，同时考虑到此时风电出力也很充裕，故不再从电网购电，盈余电力还可以通过电锅炉转化为热水供应热负荷。系统热功率的最优调度结果如图7所示。

图7 热功率调度结果Fig.7 Dispatch results of heat power

在热负荷水平较高的1：00-9：00，系统主热源联产机组保持较高的热功率输出。由于此时为风电富余时段，辅助热源电锅炉也会增加出力来消纳风电，同时为系统分担部分热负荷需求，剩余的热负荷缺口由辅助热源燃气锅炉填补。同样地，在热负荷水平较高17：00-24：00，联产机组保持较高出力水平。此时电负荷和电价也处于较高水平，风电不足以同时满足电、热负荷缺口，故燃气锅炉增加出力，成为头号辅助热源。在热负荷水平较低的10：00-16：00，由于联产机组的整体运行成本较低，仅由其供应热负荷即可满足需求，风电则用来满足电负荷的高峰需求。

系统燃气功率的最优调度结果如图8所示。

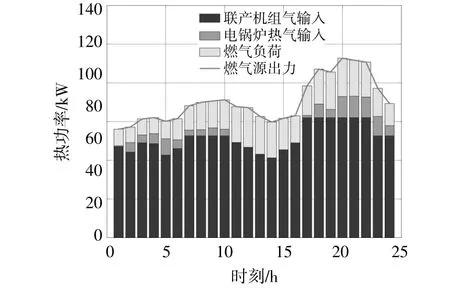
图8 燃气功率调度结果Fig.8 Dispatch results of natural gas power

在1：00-16：00，联产机组和燃气锅炉的出力维持在相对低的水平，同时燃气负荷的体量相较于联产机组的燃气消耗量很小，故此时燃气源出力处于较低水平。当联产机组和燃气锅炉的出力同 时 达 到 峰 值（17：00-23：00），燃 气 负 荷 也 处 于较高水平，此时燃气源的出力处于高峰。经优化调度后，系统总运行费用为1756.9元，其中购买燃气的成本达到了1460.4元，占比超过83%；购电费用和弃风惩罚费用仅为129.7元和166.8元。

联产机组的最优运行点如图9所示。

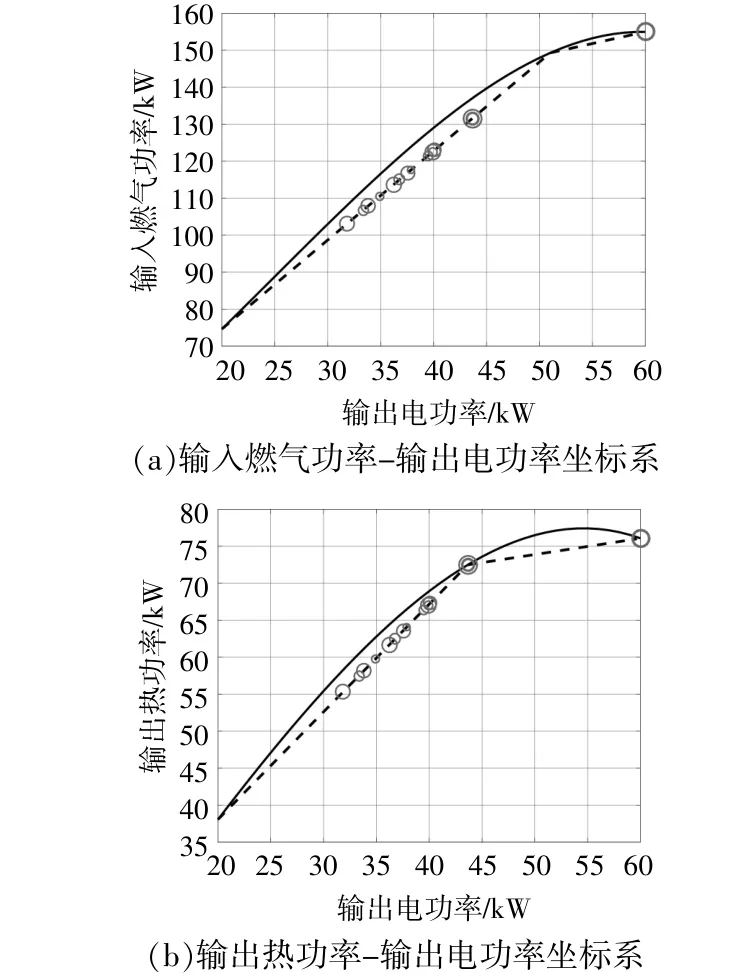
图9 联产机组最优运行点Fig.9 Optimal operation points of the cogeneration unit

由图9可以看出：在大部分时段，联产机组的输出电功率在30～45kW，此时机组燃气耗量特性的线性化误差处于较高水平；当输出电功率在40～45kW时，机组输出热功率的线性化误差相对较小；当输出电功率在30～40kW时，机组输出热功率的线性化误差处于相对较高水平。总体而言，线性化误差水平被限制在5%以内。

5 结束语

本文研究了计及设备变工况运行特性的综合能源系统日前优化调度模型及其求解方法。首先基于机理分析和实测数据将设备的变工况运行特性表示为多项式函数或分段多项式函数；然后通过增量线性化方法对目标函数和约束条件中的非线性项进行线性化处理，并针对设备变工况运行特性约束的线性化处理提出了一种基于误差控制的分段点选取方法；最后以一个电气热综合能源系统为例，对计及设备变工况运行特性的日前经济调度进行仿真分析。研究结果表明本文所提线性化处理方法与分段点选取策略能够有效求得部分非线性规划问题的近似解，并且可将近似解的误差水平限制在事先给定范围内。

需要指出的是，本文所提的基于误差控制的分段点选取方法依赖于偏差函数的极值点，能够被解析地表示为分段点的函数[式（10）]。这对于大部分多项式函数不难实现，但对于更加复杂的函数类型则未必能实现。因此，探索面向更大范围函数类型的分段点选取方法是本团队未来的工作重点之一。