THM耦合作用对EGS储层水流阻抗的影响分析

王昌龙，王 鑫，鲁进利，孙彦红

（安徽工业大学 建筑工程学院，安徽 马鞍山 243032）

0 引言

增强型地热系统（EGS）有40多年的发展历史，相关研究表明其具有广阔的应用前景[1]～[3]。根据2011年发布的《中国能源发展战略研究》，预计到2050年，我国EGS发电的装机容量有望达到300MW[4]。

EGS储层水流阻抗是影响EGS经济性能的重要参数[5]。在忽略水损失的情况下，储层水流阻抗被定义为储层中两井间的压差与注入流量之比。随着热开采过程的进行，储层温度逐渐下降，因而储层内水的流动性（密度与粘度之比）下降，导致水流阻抗增大；水流阻抗随着注入流量及储层渗透率的增大而增大，其中注入流量对水流阻抗的影响较小，而储层渗透率对水流阻抗的影响较大[6]，随着井间距和流道长度的增大，水流阻抗增大[6]，[7]。注入压力的增大，使储层平均压力增大，储层中的裂隙孔径增大，从而导致水流阻抗减小[8]。储层孔隙率、储层热导率及产出井井底压力对水流阻抗的影响非常小，而注入温度对水流阻抗的影响较大，这是因为注入温度的增大导致储层平均温度增大，从而使储层内水的粘度减小，进而 导 致 水 流 阻 抗 减 小[9]，[10]。

然而，现有文献缺乏对力学过程影响的系统分析。实际上，随着储层温度下降，储层热应力发生变化，引发岩石收缩、储层孔隙率增大，进而导致储层渗透率增大，从而减小流动阻力[11]～[13]。上述研究都忽略了力学过程。为此，本文基于前期建立的三维传热-流动-力学（THM）耦合模型[14]，对比分析THM耦合 和 传热-流动 （Thermal-Hydrologic，TH）耦合下的储层水流阻抗，系统研究力学过程对储层水流阻抗的影响。

1 模型简介

文献[14]建立的THM耦合模型不仅考虑井筒及多孔介质（包括储层、开孔及地层）中的传热传质过程，还考虑多孔介质中的力学过程。由于本文不考虑井筒中的传热传质过程，仅对多孔介质中的传热、传质及力学过程的相关理论进行阐述。

多孔介质中流体的连续性方程为

式中：φ为多孔介质的孔隙率；ρw为水的密度；t为时间；速度。

由于本文不考虑EGS中的水储存过程，因此忽略式（1）中的非稳态项。

多孔介质中流体的动量方程为

式中：pw为水的压力；重力加速度；μw为水的粘度；多孔介质的渗透率，其表达式为

式 中：kx，ky和kz分 别 为x，y和z方 向 上 的 渗 透 率分量。

本文忽略地层的渗透性，仅考虑开孔和储层的可渗透性，其中，开孔的渗透率恒定，则储层的渗透率kres为

式中：kres0为初始储层渗透率；φres0为初始储层孔隙率；φres为储层的孔隙率，其表达式为

式中：C为孔隙压缩系数；σm为平均总应力；σm0为初始平均总应力；α为Biot系数；pw0为初始水的压力。

多孔介质的力学方程为

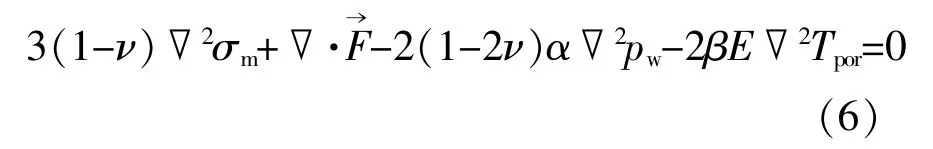
多孔介质的能量方程为

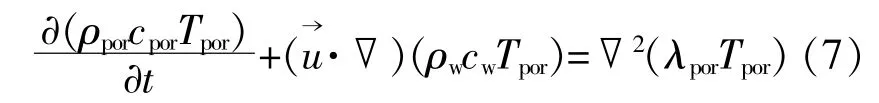
式中：ρpor为多孔介质的密度；cpor为多孔介质的比热容；cw为水的比热容；λpor为多孔介质的热导率。

多孔介质的初始条件为

式中：a为地温梯度；H为深度；θ为积分变量；ρro为岩石的密度；Tsur为地表温度。

所模拟的多孔介质区域近似于一个有缺口的长方体，可在该长方体的6个表面上设置固定的温度、压力及平均总应力边界条件（与初始时刻的值相等）。该模型更详细的介绍可见文献[14]。由于本文不考虑井筒中的传热传质过程，将开孔与井筒的两个交界处分别设置为压力进口边界条件（给定注入井筒底部压力）和压力出口边界条件（给定产出井筒底部压力）。

2 力学过程对储层水流阻抗的影响分析

储层水流阻抗IR的定义为[6]

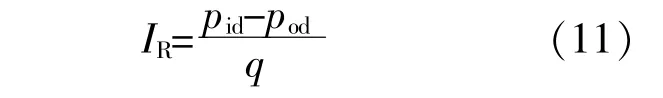
式中：pid为注入井筒底部压力；pod为产出井筒底部压力；q为质量流量。

储层内的水力传导系数K表征水在储层中流动的难易程度，其表达式为[11]

为了研究力学过程对储层水流阻抗的影响，本文以一个虚拟的EGS作为研究对象，模拟该EGS的储层水流阻抗，并对比不同的地温梯度、初始储层渗透率、注入井筒底部压力及注入井筒底部温度条件下的THM耦合和TH耦合。其中，THM耦合考虑力学过程，即储层孔隙率和渗透率随着平均总应力和水压的变化而变化，而TH耦合忽略力学过程，即储层孔隙率和渗透率均为常数。该EGS的几何尺寸如图1所示[14]。

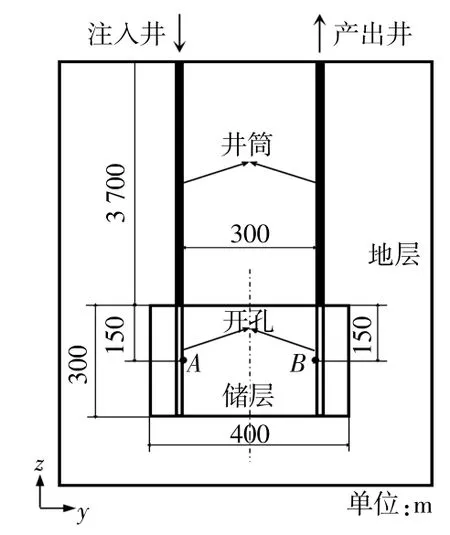
图1 EGS示意图Fig.1 EGS schematic diagram

EGS在x方向上对称，x方向上的储层尺寸为400m。该EGS的相关参数如表1所示。

表1 EGS参数Table1 EGS parameters

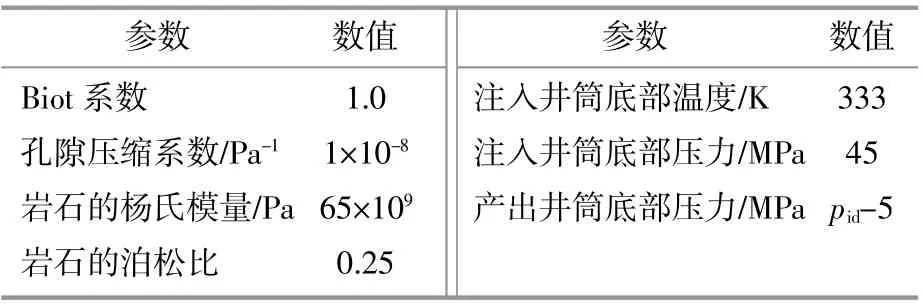
续表1

2.1 不同地温梯度条件下的力学过程影响

图2为3种地温梯度条件下THM耦合和TH耦合的储层水流阻抗的对比。

图2 不同地温梯度条件下THM耦合和TH耦合的储层水流阻抗的对比Fig.2 Comparison of the flow impedances under different geothermal gradients for THM and TH coupling

由图2可以看出，储层水流阻抗随着时间的增大而增大，其中在前期的增速较大，而在后期的增速较小。这是因为在前期注入井附近区域被快速 冷 却，导 致 该 区 域 水 的 流 动 性（ρw/μw）降 低，而 注入井是储层中的流动源，水由体积很小的注入井向周围体积很大的储层流动，因此注入井附近的阻力较大，并且在水的流动性降低的影响下其阻力增幅较大。在a=0.04，0.05，0.06K/m条件下，THM耦合的储层水流阻抗在20a内分别增大了10%，9%和6%，而TH耦合的储层水流阻抗分别增大了29%，35%和40%，可见THM耦合下的储层水流阻抗随时间变化小于TH耦合下的储层水流阻抗，这是因为TH耦合下的水的流动性不断减小，导致储层水流阻抗增大，而THM耦合下的储层渗透率不断增大，在一定程度上抑制了储层水流阻抗增大。对于THM耦合，a=0.04K/m时的储层水流阻抗分别比a=0.05，0.06K/m时的高18%，32%。储层水流阻抗随着a的增大而减小，a对THM耦合的储层水流阻抗的影响比TH耦合的大，且3种地温梯度条件下THM耦合的储层水流阻抗分别比TH耦合的低34%，42%，49%，因而在较高地温梯度条件下力学过程对储层水流阻抗的影响较大。

图3和图4分别为不同地温梯度条件下，THM耦合和TH耦合的储层内平均水力传导系数及水力传导系数分布的对比。

图3 不同地温梯度条件下THM耦合和TH耦合的储层内平均水力传导系数的对比Fig.3 Comparison of average hydraulic conductivities under different geothermal gradients for THM and TH coupling

图4 10a后不同地温梯度条件下THM耦合和TH耦合的在AB连线上的水力传导系数分布的对比Fig.4 Comparison of hydraulic conductivity distributions along the line of AB under different geothermal gradients for THM and TH coupling

储层内平均水力传导系数基本上随时间的增大而减小，而a=0.06K/m条件下THM耦合的储层内平均水力传导系数有小幅的增大，这是因为水力传导系数受储层渗透率和水的流动性的综合影响，a=0.06K/m时THM耦合的储层渗透率增大的影响大于水的流动性减小的影响。对于THM耦合，a=0.04K/m时的储层内平均水力传导系数分别比a=0.05，0.06K/m时的低19%，38%，这表明随着a的变化，储层内平均水力传导系数与储层水流阻抗的变化趋势是相反的。相比于图2中储层水流阻抗随时间的变化，图3中储层内平均水力传导系数随时间的变化较小，并且两者的变化趋势也不完全相反，说明储层内平均水力传导系数不能完全决定储层水流阻抗。图4显示在AB连线上的水力传导系数分布很不均匀，其中注入井附近的水力传导系数较小。沿着AB方向，TH耦合的水力传导系数先增大然后基本保持不变，而THM耦合的水力传导系数先增大后减小最后基本保持不变，其中减小的原因是因为储层渗透率的减幅大于水的流动性的增幅。

图5为不同地温梯度条件下THM耦合和TH耦合的储层平均渗透率的对比。THM耦合的储层平均渗透率随着时间的增大而增大，并且在较高的地温梯度条件下增幅更大。

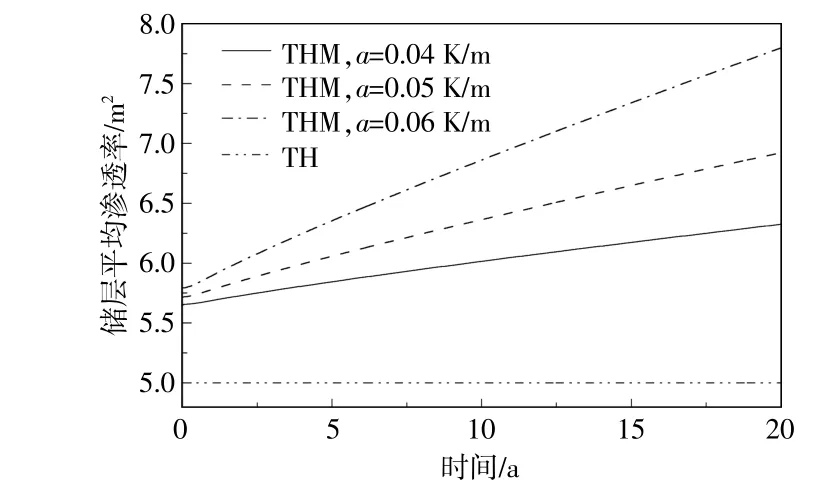
图5 不同地温梯度条件下THM耦合和TH耦合的储层平均渗透率的对比Fig.5 Comparison of average reservoir permeabilities under different geothermal gradients for THM and TH coupling

2.2 不同初始储层渗透率条件下的力学过程影响

图6为3种初始储层渗透率条件下THM耦合和TH耦合的储层水流阻抗对比。

图6 不同初始储层渗透率条件下THM耦合和TH耦合的储层水流阻抗的对比Fig.6 Comparison of flow impedances under different initial reservoir permeabilities for THM and TH coupling

kres0=3×10-15，5×10-15，7×10-15m2条 件 下 ，THM耦合的储层水流阻抗分别比TH耦合的低41%，42%，43%，因此初始储层渗透率对力学过程的影响很小。

2.3 不同注入井筒底部压力条件下的力学过程影响

图7为3种注入井筒底部压力条件下THM耦合和TH耦合的储层水流阻抗的对比。

图7 不同注入井筒底部压力条件下THM耦合和TH耦合的储层水流阻抗的对比Fig.7 Comparison of flow impedances under different injection wellbore bottom pressures for THM and TH coupling

注入井筒底部压力对TH耦合的储层水流阻抗的影响很小，而对THM耦合的储层水流阻抗的影响较大，并且THM耦合的储层水流阻抗随着注入井筒底部压力的增大而减小，这是因为较高的注入井筒底部压力导致储层渗透率增大，进而 减 小 流 动 阻 力。pid=42，45，48MPa条 件 下，THM耦合的储层水流阻抗分别比TH耦合的低39%，42%，45%，因此在较高注入井筒底部压力条件下，力学过程对储层水流阻抗的影响较大。

2.4 不同注入井筒底部温度条件下的力学过程影响

图8为3种注入井筒底部温度条件下THM耦合和TH耦合的储层水流阻抗的对比。

图8 不同注入井筒底部温度条件下THM耦合和TH耦合的储层水流阻抗的对比Fig.8 Comparison of flow impedances under different injection wellbore bottom temperatures for THM and TH coupling

注入井筒底部温度越高，储层水流阻抗越小。Tid=313，333，353K条件下THM耦合的储层水流阻抗分别比TH耦合的低47%，42%，37%，因此在较低注入井筒底部温度条件下，力学过程对储层水流阻抗的影响较大。

3 结束语

本文采用三维THM耦合模型对EGS储层水流阻抗进行模拟，通过对比THM耦合和TH耦合的模拟结果，研究了不同条件下力学过程对储层水流阻抗的影响。结果表明：相比于TH耦合，THM耦合的储层水流阻抗随时间变化的幅度减小，这是因为力学过程导致储层渗透率增大，进而在一定程度上抑制了水流阻抗增大；储层水流阻抗与储层内平均水力传导系数的变化趋势基本是相反的，然而这两者随时间的变化幅度不同且变化趋势也不完全相反，说明储层内平均水力传导系数不能完全决定储层水流阻抗；在不同条件下，力学过程对储层水流阻抗的影响强度不同，其中，在较高地温梯度、较高注入井筒底部压力及较低注入井筒底部温度条件下，其影响强度较大，而其影响强度与初始储层渗透率基本无关。