基于有限元的REBCO无绝缘线圈三维全模型及瞬态特性仿真*

赵文文,周迪帆,鲁玉明,白传易,李奇展,蔡传兵

上海大学理学院物理系,上海市高温超导重点实验室,上海 200444

1 引 言

2011年,Hahn等 人[1]首 次 提 出 高 温 超 导(HTS)无绝缘(NI)线圈,NI线圈因为具有高电流密度、高热稳定性和高失超恢复能力,所以广泛的应用于高场磁体.由于略去了匝间绝缘层,NI线圈比传统的绝缘线圈具有更紧凑的结构,因此体积电流密度更高.更重要的是,当动态励磁过程中出现局部故障或热点时,NI线圈允许多余的电流在相邻匝之间流动[2-3].因此,NI线圈显示出高电流密度、高热稳定性和高失超恢复能力的优势,这对HTS磁体的应用尤为重要.

在本文中,我们在三维FE模型中集成了电路和热模块,并模拟了高场磁体的NI线圈的传输特性.我们利用这个模型研究了NI线圈在充电过程中的充电延迟特性、充放电过程中的环向和径向电磁传输行为以及匝间接触电阻对励磁过程和线圈热稳定性的影响,最后我们还讨论了不同金属绝缘材料对线圈热稳定性的影响.这些结果与使用分析性等效电路模型计算的结果表现出良好的一致性.

2 模型建立

在模型中我们采用的REBCO超导带材是由上海上创超导科技有限公司制备,在表1中我们列出了REBCO带材和线圈的详细参数.

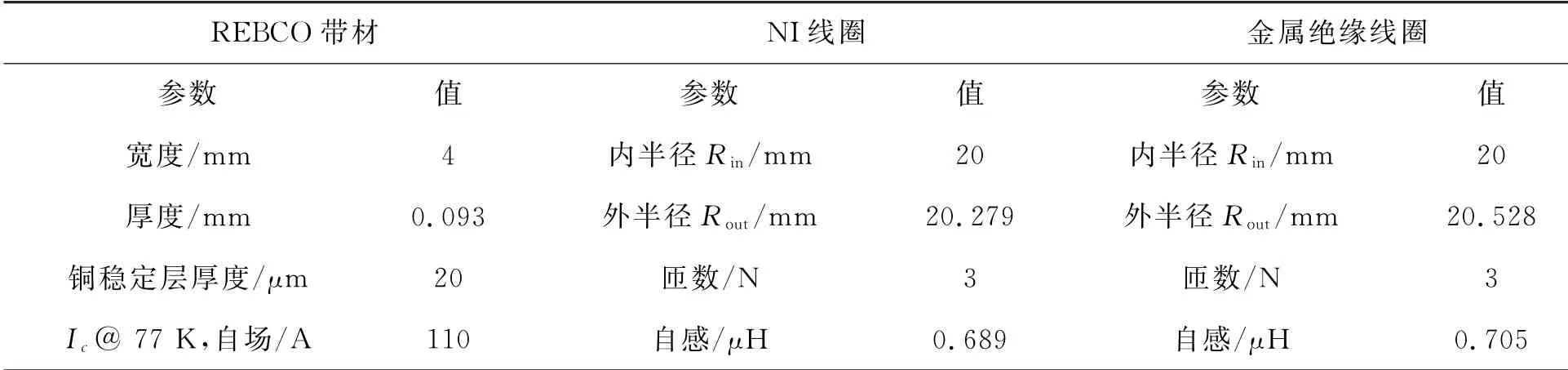
表1 REBCO带材和线圈的详细参数

2.1 等效电路模型

根据Qin等人[6]提出的分析性等效电路模型(ECM),NI线圈内的电流在励磁过程中可以被分解为环向和径向分量.他们将线圈的每一匝作为一个基本的电路单元,每一个电路单元由三个电路参数R s、R r和L组成.R s代表基于E-J关系的超导层的电阻[12],R r为径向电阻,由铜层电阻和接触电阻组成.L代表线圈的电感.因此,整个线圈可以用一个等效电路来表示,所有这些电路单元都串联起来,形成一个同轴的环形,部分电路图如图1所示.

图1 线圈的等效电路模型图

根据基尔霍夫定律和第二代高温超导体的E-J关系[13-14],可以得到每个基本电路单元的方程式为:

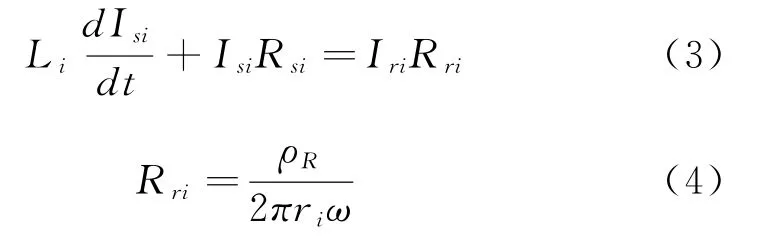
在这些公式中,I si、I ri和I op分别代表环向电流、径向电流和工作电流;I c是77 K时的临界电流,V ci是线圈的第i匝电压;ρR是匝间接触电阻率,这里,我们设定NI线圈的匝间接触电阻率为10μΩ·cm2[8],不锈钢共绕线圈的匝间接触电阻率为362.4μΩ·cm2[15];r i是第i匝线圈的半径,w是超导带的宽度;指数n被设定为21[16].

2.2 3D FEM模型

分析等效电路模型以显著的计算速度给出了NI线圈的宏观分析,已被广泛用于高场磁体的设计.然而,仍需要进行有限元模拟来揭示NI线圈的详细电磁传输和热行为.我们根据NI线圈固有的轴向不对称性建立了它的三维全模型.图2(a)显示了局部三维NI线圈模型.这里我们只考虑了HTS带材的超导(SC)层和铜层以进行简化.模拟是用Comsol软件实现的.

对于绝缘线圈的有限元模拟,通常采用逐点约束的方式对线圈施加电流.由于总电流的守恒,这种激励方法对于NI线圈是不可行的,因为电流可以同时在环向(J s)和径向(J r)方向流动.在这里,我们通过将线圈的励磁方式设置为建立NI线圈模型的“电路”方法,将电路模块集成到AC/DC模块中,通过外部电路对NI线圈进行励磁,因此线圈中的电流没有任何约束,如图2(b)所示.我们将线圈的一端定义为电流流入端,另一端定义为电流流出端,如图2(c)所示.

基于麦克斯韦方程和HTS超导体的E-J关系,我们可以得到NI线圈模型的控制方程为:

随着技术进入商业化，碟式太阳能热发电系统的建模和仿真对于预测各种运行条件下的性能变得越来越重要。本研究对系统的各个部件进行数学建模并计算在典型工作条件下各个部件的热效率和 效率[1]，评估各个部件的性能，然后串联成整个系统，评估整个系统的性能。

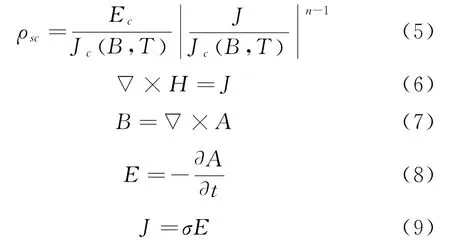
其中E c是1μV/cm的标准,对于REBCO带材,指数n被设定为21[16],其中J c是临界电流密度,它与温度和磁场都有关.σ代表材料的电导率,包括超导材料和铜材料.图2(c)显示了NI线圈的网格.

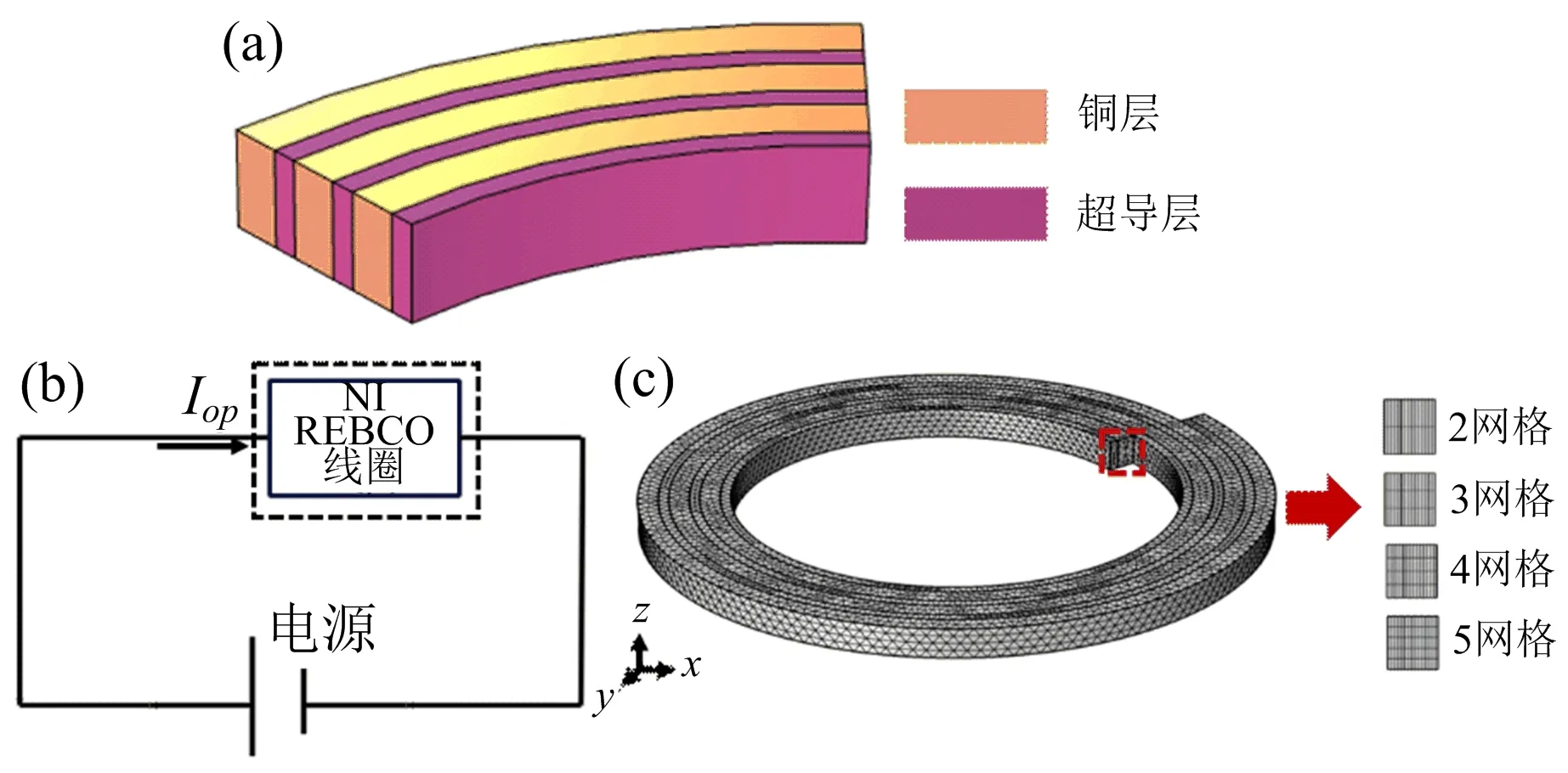
图2 (a)NI线圈模型,(b)励磁电路示意图,(c)有限元模型的网格

失超保护和失超恢复是NI线圈的关键特征之一.考虑到这一点,我们还将固体加热模块耦合到我们的模型中,以研究励磁过程中的热传播.临界电流密度和临界温度(T c=90 K)之间的关系表示为[17]:

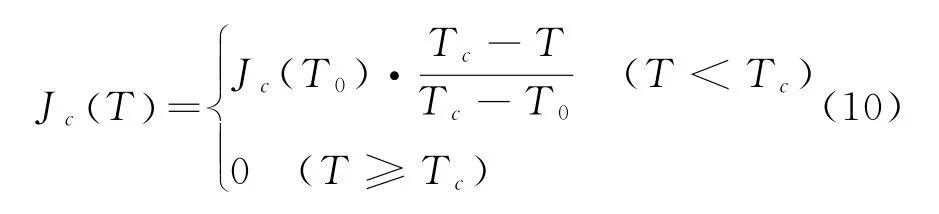
其中T0、T c分别设定为77 K和90 K.

而临界电流密度J c对磁场B的依赖性,包括HTS带材的各向异性特征,是用改良的Kim模型来描述的[18]:

B‖和B⊥是磁通密度的平行和垂直分量.参数B0、k和a的值分别为42.6 m T、0.295和0.7[18-19].

为了在失超过程中超导态过渡到正常态期间实现连续的电阻率,使用了Duron等人[20-21]提出的修正电阻率:

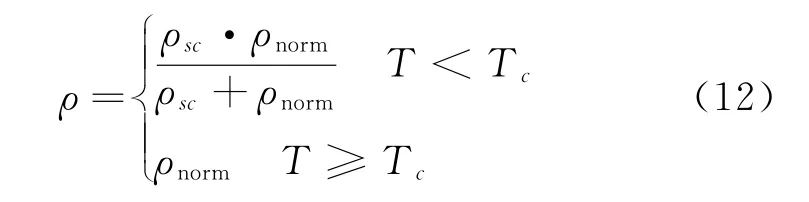
其中ρnorm指的是REBCO超导材料在正常状态下的电阻.这里定义为2.8×10-9Ω·m[22].对于匝间接触电阻率根据参考文献[8]和[15],NI线圈为10μΩ·cm2,不锈钢共绕线圈为362.4μΩ·cm2.

我们将NI线圈剖分出不同的网格数,分别沿着z轴方向划分为2、3、4、5网格,如图2(c)所示,并且将不同的网格所需的计算时间列于表2.我们分别通过有限元方法和数值计算方法获得了NI线圈在充电过程的总损耗,并对二者进行了比较,细节将在下一节中讨论.可以发现,随着自由度的增加,两种模型的计算结果越来越吻合.通过在z轴方向上设置5个网格的剖分方式产生了一个令人满意的结果,二者误差为0.32%,因此在本研究中的所有模拟中都选择了在z轴上剖分5个网格的方式.

表2 不同网格数的计算结果

3 数值计算法和有限元方法的结果比较

首先,我们用分析等效电路的方法计算了四个不同励磁速率的励磁过程中随时间变化的环向和径向电流.结果显示在图3中.我们选择0.7I c作为目标工作电流,并在达到目标电流后保持稳定.从图3中我们可以清楚地发现,匝间电流随着励磁速率的增加而增加.因此,超导带中的环向电流减少了,实际励磁时间要比达到目标电流的时间更长,从而导致了充电延迟现象.

图3 ECM模型在不同励磁速率下环向电流和径向电流的随时间演变

其次,在不同的励磁速率下,整个励磁过程中的欧姆损耗[23]可以计算为:

其中,Q r是由于匝间接触电阻和径向电流分量造成的欧姆损耗,Qsc是基于E-J关系得出的超导指数损耗.对于0.1 A/s、1 A/s、5 A/s和10 A/s的励磁速率,总损耗分别为1.534×10-6W、1.848×10-5W、5.061×10-5W和5.859×10-5W.

接下来,我们用提出的有限元模型模拟了励磁过程.在这里,我们构建了一个九匝的NI线圈.我们选择0.7I c作为目标工作电流,并在其达到目标值后保持稳定.在有限元模型中,通过对环向电流密度(J s)和径向电流密度(J r)进行积分,我们得到环向电流(I s)和径向电流(I r)分别为:

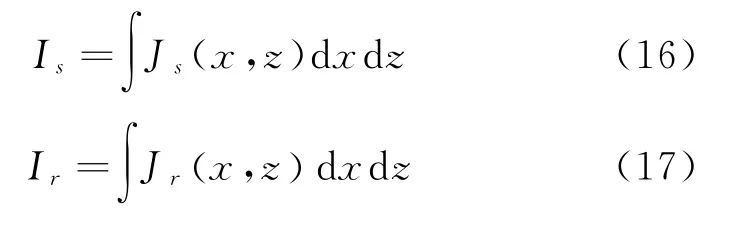
图4显示了有限元模型计算的环向和径向电流,充电延迟和径向电流随着励磁速率的增加而增加.此结果与分析计算模型得到的结果高度一致.

图4 FEM模型在不同励磁速率下环向电流和径向电流的随时间演变

4 无绝缘高温超导线圈的瞬态电热分析

在下面的有限元模型中,如图5所示的三角形波形被用于励磁电流.第一个上升的周期用于励磁过程,而更多的周期用于动态分析.

图5 无绝缘线圈的励磁波形图

图6表明了NI线圈在不同时刻的环向电流分布图,(a)、(b)、(c)、(d)分别对应于图5中标记的四个时刻.当对NI线圈励磁时,电流主要流向超导层,而流向铜层的电流很小,但不是零.铜层作为一个分流电阻,随着输运电流的变化而变化,从而导致了充电延迟.

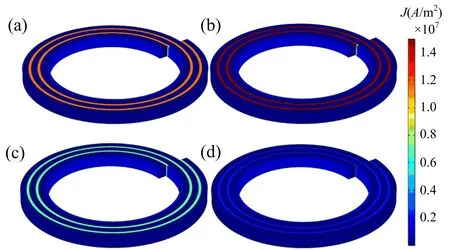
图6 a、b、c和d四个不同时刻的环向电流密度

4.1 匝间接触电阻对无绝缘线圈的电热特性影响

无绝缘线圈的接触电阻是忽略了带材厚度的等效匝间电阻率,其单位为μΩ·cm2,其值的大小与温度、材料、匝间压力等多种因素有关,考虑到基于二代高温超导带材的无绝缘线圈通常在恒定张力下绕制而成,一般假定接触电阻在各匝的分布是均匀的.研究表明,无绝缘高温超导线圈在液氮(77 K)下的匝间等效电阻率一般为10～100μΩ·cm2[24].图7中我们给出了接触电阻分别在20、50、80和100μΩ·cm2条件下无绝缘线圈的环向电流和径向电流分布图,从图中我们可以看出,随着匝间接触电阻的增大,无绝缘线圈的径向电流逐渐减小,NI线圈的充电延迟现象明显改善.而且在图8中我们给出了四个接触电阻下的无绝缘线圈温度分布图,从图中我们可以看出,当我们在匝间等效电阻率范围内改变其接触电阻时,对其热稳定性几乎没有影响.

图7 不同接触电阻下无绝缘线圈的环向电流与径向电流分布图

图8 不同接触电阻下无绝缘线圈的温度分布图

为了进一步分析接触电阻对无绝缘线圈的影响,我们将不锈钢带与无绝缘线圈并绕,增大线圈的接触电阻率.从图9中我们可以看到,虽然金属绝缘线圈明显改善了充电延迟现象,但却破坏了线圈的热稳定性,导致线圈局部失超,并且在线圈的接头处温度最高.这是因为高电阻率的不锈钢层会使径向方向的电流流动受到限制,阻碍了热量的扩散,从而导致热量积累,线圈失超.

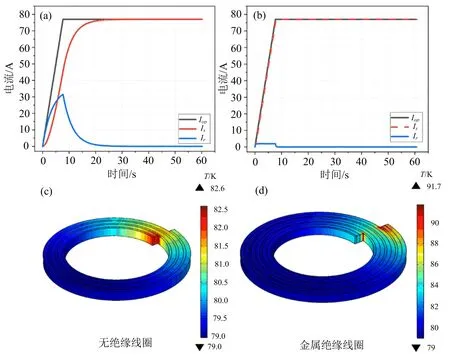
图9 无绝缘与金属绝缘线圈的电流分布和热稳定性对比图

4.2 不同金属绝缘材料的影响

为了研究金属绝缘材料对无绝缘线圈的热稳定性影响,我们考虑了一些具有代表性的材料,如铜(Cu)、黄铜(BS)、不锈钢(SS)和哈氏合金(HT),这些材料基本上涵盖了金属绝缘材料的全部电阻率范围.同时,为了评估热参数的影响,在计算中还采用了附加的金属绝缘材料(CS),其既具有不锈钢的电阻率又具有铜的热参数.图10给出了上述不同金属材料并绕下金属绝缘线圈的温度分布图,从图中我们可以看出具有较高电阻的金属绝缘体材料使线圈具有较高的稳定温度.这意味着高电阻率的金属绝缘材料会恶化线圈的热稳定性,但具有一定的局限性.它可以通过以下现象得到证明:具有相似热导率的不锈钢并绕的(SS)和哈氏合金并绕的(HT)金属绝缘线圈达到了差别不大的稳定温度,而哈氏合金的电阻率是不锈钢的两倍.这一发现揭示了低电阻率的金属绝缘材料可以通过其突出的分流能力提高热稳定性.另外一个值得注意的发现是,具有较高热导率的金属绝缘材料可以稍微提高线圈的稳定性,因为它可以通过提高热传播速度来降低线圈的温度,提高热稳定性,这可以从不锈钢并绕的(SS)和附加的金属绝缘材料(CS)的对比中发现.因此,综合考虑上述情况,具有低电阻率和高热导率的金属绝缘材料是实现金属绝缘线圈良好性能的最佳选择.

图10 不同金属绝缘材料的线圈温度分布图

5 结 论

在这项研究中,我们为NI线圈提出了一个完整的三维有限元模型.这个模型使用了AC/DC模块和电路模块,以便能够直接分析NI线圈的传输特性.首先,我们计算了无绝缘线圈在不同励磁速率下励磁过程中的损耗,这与等效电路模型取得的结果达到了很好的一致性;其次,通过这个模型,我们得到了NI线圈的环向电流分布图;最后,我们对比分析了不同接触电阻大小以及不同金属绝缘材料对无绝缘线圈的热稳定性影响.我们得到了在无绝缘线圈的接触电阻大小范围内,增大匝间接触电阻可以有效改善无绝缘线圈的充电延迟现象,而且不影响线圈的热稳定性.但是,当我们进一步增大线圈的接触电阻,将不锈钢带与无绝缘线圈并绕,同样可以极大的改善线圈的充电延迟现象,却破坏了线圈的热稳定性,导致线圈失超.另外,通过对比证明,低电阻率和高热导率的金属绝缘材料是金属绝缘线圈的最佳选择,既改善了无绝缘线圈的充电延迟,又在一定程度上保证了线圈的热稳定性.

这个新提出的模型揭示了关于环向和径向特性的更详细的信息,并以更高的保真度预测了电流和温度的演变,为无绝缘线圈的设计和保护提供了合理的参数和预测.