不同孔道形状对DPF再生性能的影响研究

2022-10-21卢志美覃神全李艳勤黎华扬

装备制造技术 2022年7期

卢志美，覃神全，李艳勤，黎华扬

（广西玉柴动力股份有限公司，广西玉林 537005）

0 引言

柴油机微粒捕集器（DPF）作为降低PM最有效的后处理装置之一，凭借其简单高效的工作特性被广泛应用于交通运输、工程机械、农业机械、发电等领域[1]。

DPF在颗粒过滤期间，过滤效率高达90%以上[2]，甚至在形成烟灰层后能达到100%[3]。但由于DPF孔道内的容积有限，颗粒沉积过多将导致排气压降升高，不利于发动机正常工作，因此必须以定期燃烧的方式去除颗粒物实现DPF再生[4]。但在DPF再生过程中碳烟颗粒燃烧会产生局部高温，容易损坏DPF的孔道结构，需要对其孔道结构进行合理的优化设计。

目前，已经有许多学者研究了孔道结构对DPF工作特性的影响。Nakamura等[5]将载体通道由标准正方形几何体变为正弦波形的通道时。结果表明，增大过滤面积能够降低其背压。Ingram等[6]设计了非对称通道结构的DPF，将入口通孔增大，出口保持不变。研究发现：同样颗粒存储量的情况下，非对称DPF的压降仅是标准DPF的一半。Segawa等[7]研究发现六边形非对称通道过滤器具有较大的开放通道面积，并且其压降低于方形对称通道过滤器。

目前对DPF孔道结构的研究主要集中在颗粒捕集阶段方面，而模拟不同形状孔道比对主动再生过程中的再生性能的研究鲜有报道。因此，采用三维模型研究了不同形状孔道结构对其主动再生过程中温度场、压降和再生效率的变化规律，对DPF再生过程中的结构优化设计具有重要的参考意义。

1 数学模型

1.1 气相控制方程

质量守恒方程：

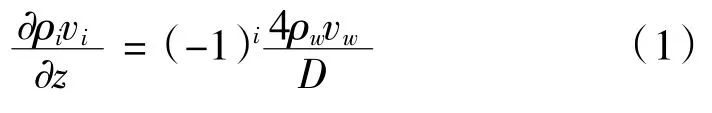
动量守恒方程：

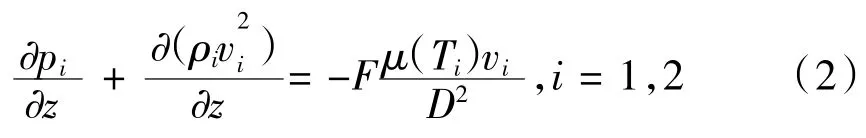
能量守恒方程：

式中：i为气体通道，i=1为进气道，i=2排气道；w为壁面厚度；ρ为气流密度；v为通道的气体流速；z为通道中的轴向方向；p为气体压力；F为方形通道内的压降系数，取值为28.45 Pa；μ为排气的动力黏度；T为内气流的混合温度；cp为气体的比热容，hi为过滤体孔道气流与过滤体壁面之间的对流换热系数。

1.2 固相控制方程

质量守恒方程：

能量守恒方程：

式中：ρp为颗粒层密度，wp为颗粒层厚度；Mc表示碳的分子量；MO2表示氧气的分子量；Y1为进口通道的氧气浓度；Sp为被捕集的微粒层的比面积；cp，p是颗粒层的比热；ws为过滤壁厚；cp，s是过滤器壁的比热容。

燃烧热Qreact满足方程：

式中△HO2为反应生成焓。

对流热传导Qcond满足方程：

式中，λp为颗粒层的导热率；λw为过滤层的导热率。

氧气组分在壁面上满足平衡方程：

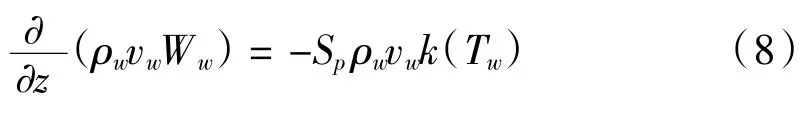
式中，Ww为壁中的含氧量。

1.3 压降控制方程

气流经过DPF载体产生压降损失，过滤壁面和颗粒层被视为两个相连的多孔介质层，压降损失遵从达西定律，即

式中，kp和ks分别为颗粒层和壁面的渗透率。

1.4 反应机理

DPF的主动再生通过直接提高进气温度使碳微粒与氧气发生氧化反应，主要化学反应机理如下：

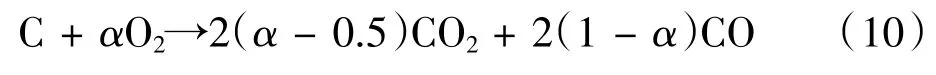
在等式（10），α为碳颗粒氧化反应的完全系数，一般为0.55～0.90。碳粒子氧化反应的焓ΔH可以表示如下

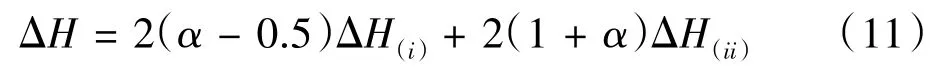
其中ΔH（i）和ΔH（ii）分别是CO2和CO的形成焓，J/mol。

1.5 孔道结构

标准的DPF孔道是方形的壁流式结构。为了研究不同孔道结构对DPF再生性能的影响，提出了两种用于过滤器的不同通道结构，。3种孔道结构分别为正方形、六边形和八边形，如图1所示。

图1 DPF的不同通道形状

2 物理和数学模型

DPF主要由进气管路、滤芯和出气管路三部分组成。本研究采用壁流式碳化硅DPF，具体的结构参数见表1。采用AVL-FIRE软件进行模拟计算，进气道和出气道的网格设置为5 mm，燃烧区域的网格为3 mm。DPF的计算网格如图2所示。

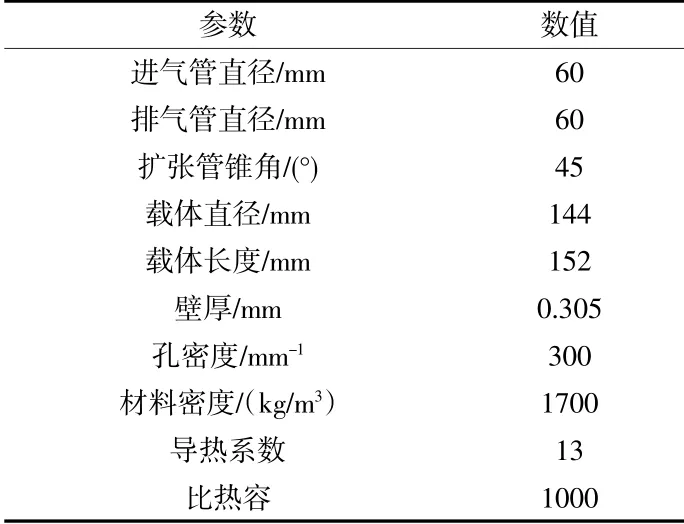
表1 DPF结构参数

图2 DPF计算网格

3 模型验证

为了验证上述数值计算模型的准确性，对DPF再生过程进行了大量的建模和数值模拟研究，本研究得到的模拟结果与Mayari的试验数据进行了验证[8]。其中，模型验证计算过程所需的排气状态参数和过滤器结构参数与文献中的参数保持一致。模型求解参数见表2。图3显示了在DPF中心轴上三个位置的壁温测量结果和数值模拟结果的比较。显然，由该图可以看出当前研究的模拟结果和文献中的试验结果之间有良好的一致性，且误差较小，验证了模型的准确性和可靠性。

图3 模型验证

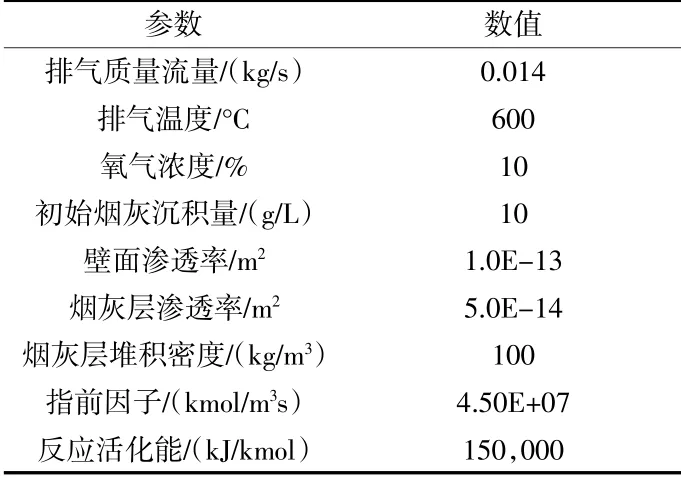
表2 模型求解参数

4 结果与分析

4.1 不同孔结构对温度场的影响

在不改变DPF过滤体其他参数的情况下，改变过滤体的孔道结构，研究其对再生过程的影响。根据八边形通道的DPF在145 s时候达到峰值温度，壁面峰值温度为1164.82 K（图4）。六边形结构在190 s的时候达到峰值温度，为1097.45 K。而方形孔道峰值温度在200 s的时候达到1084.53 K的峰值温度。3种孔道结构中，正方形结构峰值温度出现的时间点最晚，峰值温度也最小。这是因为八边形孔道的入口通道与出口通道相比来说，入口通道的密度大于出口通道，就导致每个入口通道中的烟灰分布较为均匀，燃烧得更充分，产生的热量更高且更集中，且加上密度较少的出口通道不利于热量排出，就容易导致峰值温度出现得更快且更高。

图4 不同孔结构对再生峰值温度的影响

4.2 不同孔结构对压降的影响

DPF再生过程中不同孔结构对压降的影响如图5所示。可以看出，虽然初始的烟灰颗粒容量是一样的，但由于微粒在DPF孔道中的分布不同，导致初始的压降也不一样。其中，八边形孔道的初始压降最高，正方形孔道的次之，六边形孔道的初始压降最低。这是因为微粒在入口处的微粒较少，对气流的流动阻力较少，故压降最小。随着DPF的再生，由于温度升高导致气体膨胀，加速微粒无规则运动，碰撞几率变大，气体黏度增加，导致流动阻力增大，从而使压降升高。其中八边形孔道的烟灰颗粒所产生的压降最高，这是因为即使在相同的颗粒容量下，均匀分布的微粒所能容纳的微粒也是最多的，再生燃烧过程中所产生的温度也就越高，从而导致更大的压差。

图5 手动控制界面

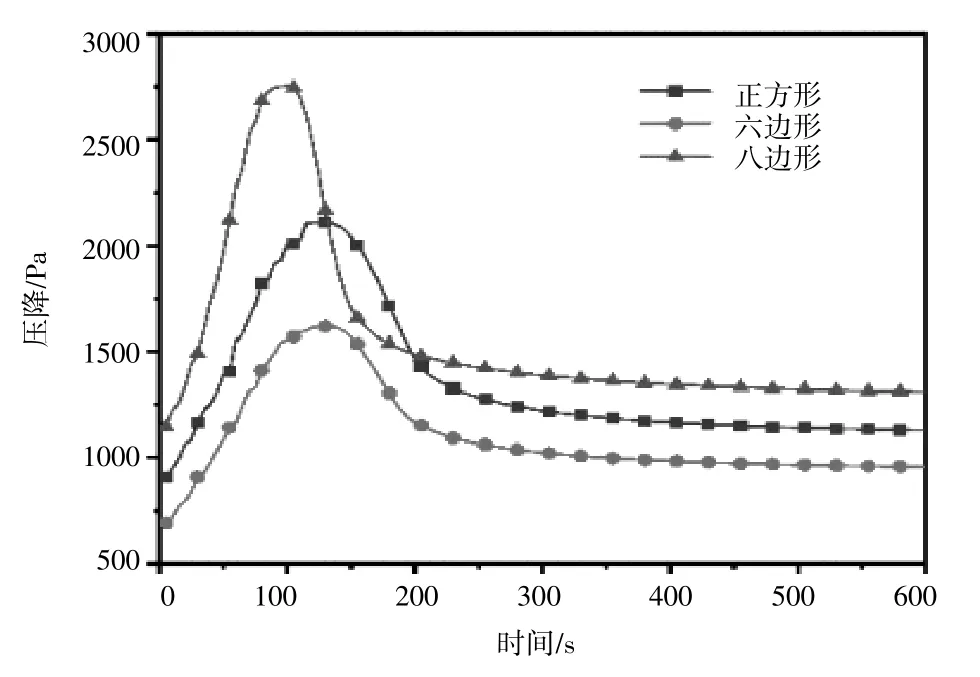
图5 不同孔结构对再生压降的影响

4.3 不同孔结构对再生速率的影响

图6为不同形状的进出孔道DPF的碳载量随时间的变化关系。由图可知，在未达到再生温度初期，碳载量保持不变。当达到再生温度后，八边形孔道DPF的碳载量首先开始下降，且下降趋势最为迅速。六边形的下降趋势次之，正方形的最慢。再生结束后，八边形DPF载体内残留的碳烟质量更小。这是因为过滤体直径和通道密度不变时，八边形孔道使得进气孔道表面碳烟层面积增大，与排气接触面积增加。在再生过程中，由于八边形孔道DPF热量排出较慢，排气与载体壁面的热交换更多，使得再生速度较快，总体的再生效率也有所增大。