滑带土抗剪强度参数取值研究
——以黄冈市片麻岩类堆积层滑坡为例
2022-10-20朱文慧
朱文慧, 邹 浩, 石 威, 陈 兵, 毛 帅, 王 超
(湖北省地质局 第三地质大队,湖北 黄冈 438000)
滑带土抗剪强度参数取值是滑坡稳定性评价与滑坡治理工程设计中的关键问题,长期以来受到国内外学者的广泛关注[1-2]。滑带土抗剪强度参数c(黏聚力)、φ(内摩擦角)广泛应用在滑坡破坏概率计算[3-4]、可靠度分析[5-6]、滑坡危险性评价、滑坡预测预报以及防治工程设计中。滑带土抗剪强度参数取值方法很多,如室内试验、现场大型剪切试验、工程地质类比法和参数反演计算等。但是由于滑带土经历了不同的地质与力学过程,其矿物成分、土层埋深、应力状态、含水率和质量密度等特征不同,即使在相同地区的某类岩体中也存在一定差异;同时滑带土抗剪强度参数在试验测试阶段,由于在取样、运样、制样中受到扰动以及在试验方法和技术上的不同,其测试结果也必然存在一定差异,这就导致滑带土抗剪强度参数的变异性更加明显。
近年来,国内外学者围绕土体抗剪强度参数问题开展了较多研究。Lee et al.[7]利用ANN(artificial neural network)人工神经网络模型建立了非饱和土的表观黏聚力预测模型,预测了非饱和土的抗剪强度参数;周葆春等[8]采用Fredlund公式对比预测和实验结果的误差预测非饱和土c、φ值;魏应乐等[9]通过统计41组岩体的强度参数,采用多元非线性统计分析模型求得强度解析解;Langejan[10]认为土体的抗剪强度参数服从正态或者对数正态分布;Lumb[11]在统计分析了113组香港淤泥质土的剪切试验结果后,认为土体抗剪强度参数服从正态分布;李远耀等[12]通过统计三峡库区400余处滑坡,认为该区发育的滑坡滑带土抗剪强度参数基本服从正态或对数正态分布。
本文以黄冈市片麻岩类堆积层滑坡为例,统计其滑带土抗剪强度参数取值,运用数理分析方法研究其在天然和饱和两种工况下的特性与取值置信区间,利用IBM-SPSS与Minitab建立强度参数的概率分布函数,再结合直剪试验得到滑带土抗剪强度参数c、φ的试验值,分析设计值与土工试验值的相关性,提出黄冈市片麻岩类堆积层滑坡滑带土抗剪强度参数的最优取值区间与取值方法。
1 滑带土抗剪强度参数特性研究
确定准确的滑带土抗剪强度参数是滑坡稳定性评价与设计的基本要求,然而地质体的样本趋近于无穷,对其开展无限次抽样工作是不切实际的。在工程应用中,不论样本的数据量是否足够,其概率分布形式是其首要的研究对象。因此,目前比较合理的方法是利用子样本的分析来推导样本总体的规律,而实现这一切的前提条件是收集到符合要求的子样本。本研究通过收集整理滑带土抗剪强度参数,确定样本容量后,再对其进行数理统计分析,寻找子样本的规律特征,由此得到典型的特征值,为滑坡稳定性设计和评价提供可靠的依据。
1.1 滑带土抗剪强度参数取值统计
黄冈市目前已治理的51处片麻岩类堆积层滑坡,经历了3~6年的检验未发生明显变形,表明其稳定性评价是可信的,其滑带土抗剪强度参数c、φ情况如表1所示。由表1可知,在天然工况下,黏聚力c1为10.5~30 kPa,内摩擦角φ1为8°~29°;在20年一遇暴雨饱和工况下,黏聚力c2为9.5~27 kPa,内摩擦角φ2为6°~27°。
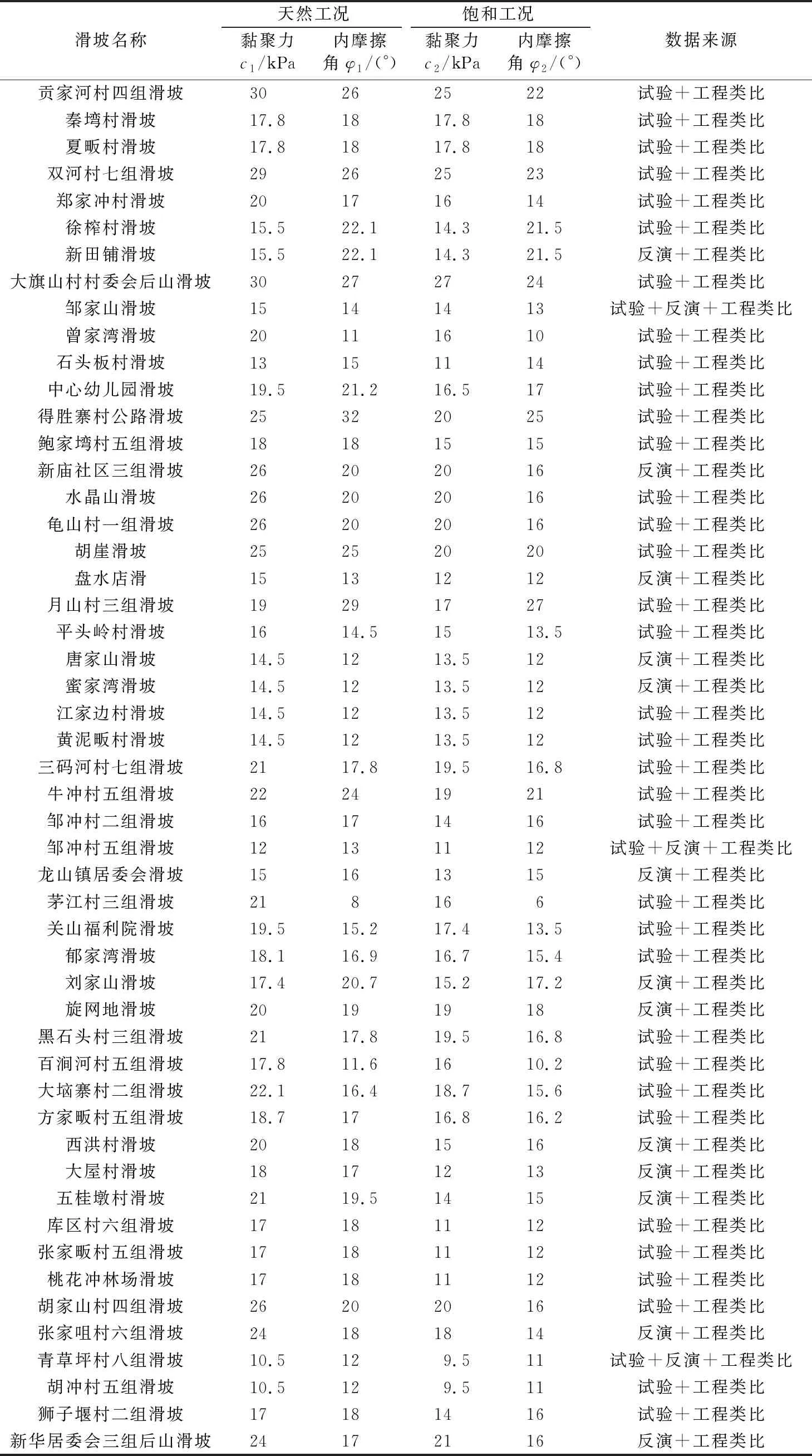
表1 滑带土抗剪强度参数表
1.2 滑带土抗剪强度参数特性分析
通常一组数据中可能会存在一个或多个异常大或异常小的值,这样的极端值称为异常值,这些异常值会导致整体数据特征发生偏移。箱形图可以用来观察数据整体的分布情况,正常数据均处于箱体内,而异常数据则出现于箱体上边界和下边界以外。异常数据的辨别方法以四分位数和四分位距为基础,利用Minitab软件得到基于实例统计的滑带土抗剪强度参数取值箱形图(图1)。由图1可看出:①天然工况下黏聚力c1箱形外无偏离值,箱形上部触须明显长于下部触须,说明c1数据是偏态分布的;②天然工况下内摩擦角φ1的箱形外有异常数据,通过软件读取显示为月山村三组滑坡;③饱和工况下黏聚力c2箱形外无偏离值,箱形上部触须明显长于下部触须,说明c2数据是偏态分布的;④饱和工况下内摩擦角φ2的箱形外有异常数据,通过软件读取显示为月山村三组滑坡。因此,需要对异常数据进行剔除,再进行天然和饱和工况下强度参数统计学区间分析。
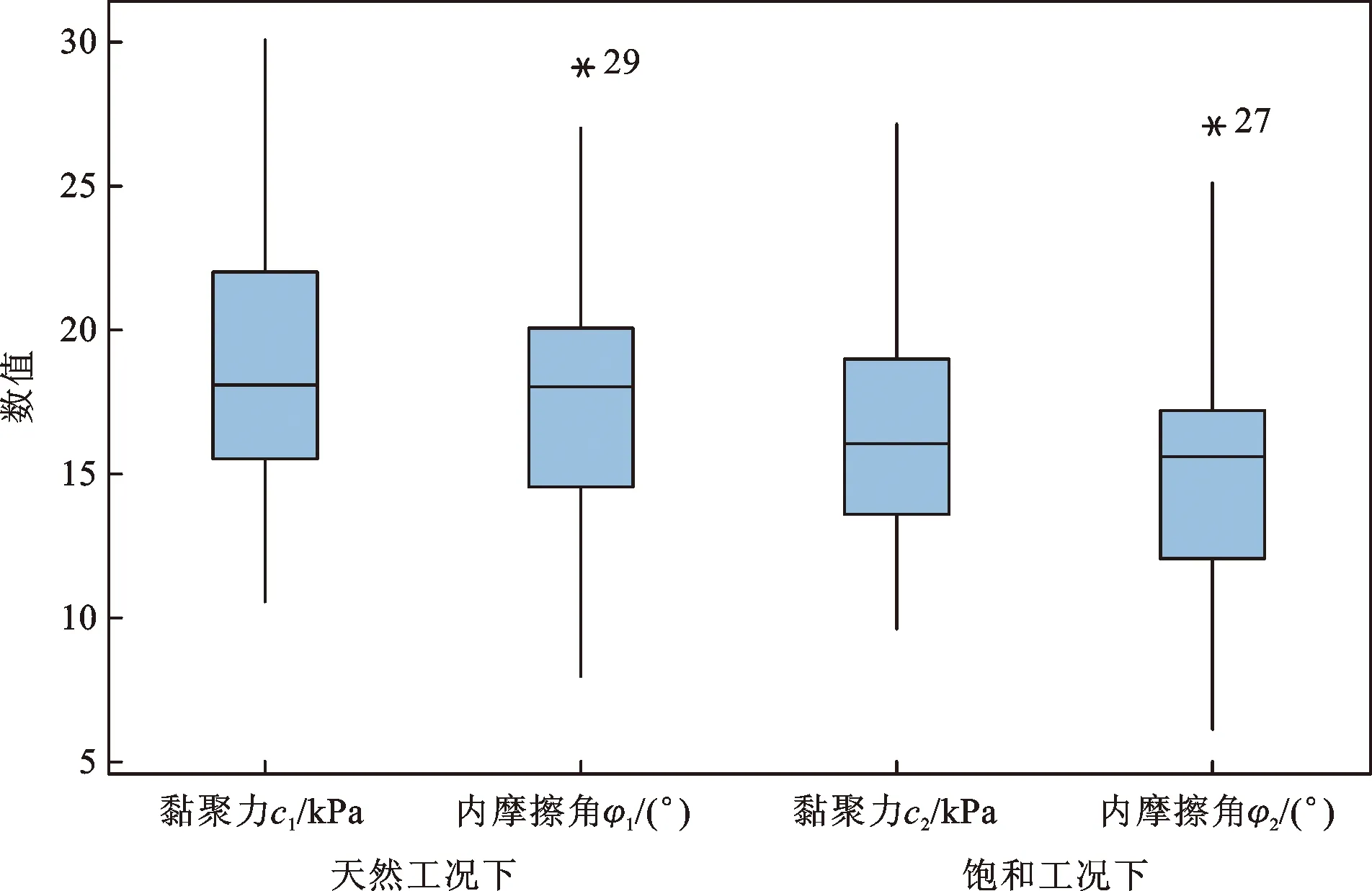
图1 滑带土强度参数取值箱形图
本研究采用单个标准差计算置信区间(95%),获得基于实例统计的滑带土抗剪强度参数取值区间(表2)。由表2和图2可知:天然工况下黏聚力c1为17.75~20.43 kPa、内摩擦角φ1为16.41°~19.00°;20年一遇暴雨饱和工况下黏聚力c2为14.99~17.19 kPa、内摩擦角φ2为14.42°~16.74°。

表2 滑带土抗剪强度参数数理分析统计表

图2 滑带土强度参数取值置信区间图
综合以上,黏聚力和内摩擦角的数据集在天然工况下均大于饱和工况,且从天然工况转化至饱和工况时,黏聚力数据集的变化比内摩擦角数据集的变化范围大;黏聚力的变异系数均比内摩擦角大,说明抗剪强度参数在天然工况转化至饱和工况的过程中,黏聚力的波动大、变幅大,内摩擦角的波动小、变幅小,即片麻岩类堆积层滑坡遭遇强降雨时,滑带土的黏聚力比内摩擦角减小的幅度更大,说明降雨对黏聚力的削减作用比对内摩擦角的影响更为明显。
2 滑带土抗剪强度参数取值研究
对于目前滑带土抗剪强度参数取值的研究,主要是通过统计样本数据规律从而对样本数据总体的分布进行估计[13-14]。强度参数取值特性主要由概率分布函数表征,均值和方差代表了随机变量的最优估计。强度参数的均值和方差主要是通过统计分析样本数据得出。基于前文统计分析所用数据,通过其平均值和标准差等特征值,可以得到这些随机变量的分布特性,建立对应的概率分布函数。本文所用经验分布主要是参考前人关于土体抗剪强度参数c、φ值概率模型的相关研究,假设滑带土抗剪强度参数c、φ值的分布为正态分布和对数正态分布。
2.1 滑带土抗剪强度参数概率分布函数研究
本研究采用IBM-SPSS P-P概率图对片麻岩类堆积层滑坡样本c、φ值在天然和饱和两种工况下进行分布检验(图3、图4)。P-P概率图可检验样本实际累积概率分布与预期累积概率分布是否吻合,若吻合,则散点应围绕在一条直线附近。其原理在于如果数据正态,那么数据的累积概率与正态分布累积概率基本保持一致。首先分别计算出数据实际累积概率和假定正态时的累积概率;再将实际累积概率作为X轴、对应正态分布累积概率作为Y轴,形成散点图。

a.c1正态P-P图;b.φ1正态P-P图;c.c2正态P-P图;d.φ2正态P-P图

a.c1对数正态P-P图;b.φ1对数正态P-P图;c.c2对数正态P-P图;d.φ2对数正态P-P图
由上述强度参数c、φ值P-P图可知:天然工况下黏聚力c1、饱和工况下黏聚力c2与内摩擦角φ2的散点分布更服从对数正态分布;而天然工况下内摩擦角φ1的散点分布更服从正态分布。因此,可采用正态分布和对数正态分布概率函数来表征和预测抗剪强度参数的随机特性。
正态分布的概率分布函数为:
(1)
对数正态分布的概率分布函数为:
(2)
式中:x为强度参数的随机变量;σ为强度参数的总体标准差统计量;μ为强度参数总体均值统计量。
将前文滑带土抗剪强度参数值在天然和饱和工况下的标准差σ与均值μ代入上述函数公式,可得到c、φ值的概率分布函数(表3),再利用Minitab软件得到其函数分布图(图5)。
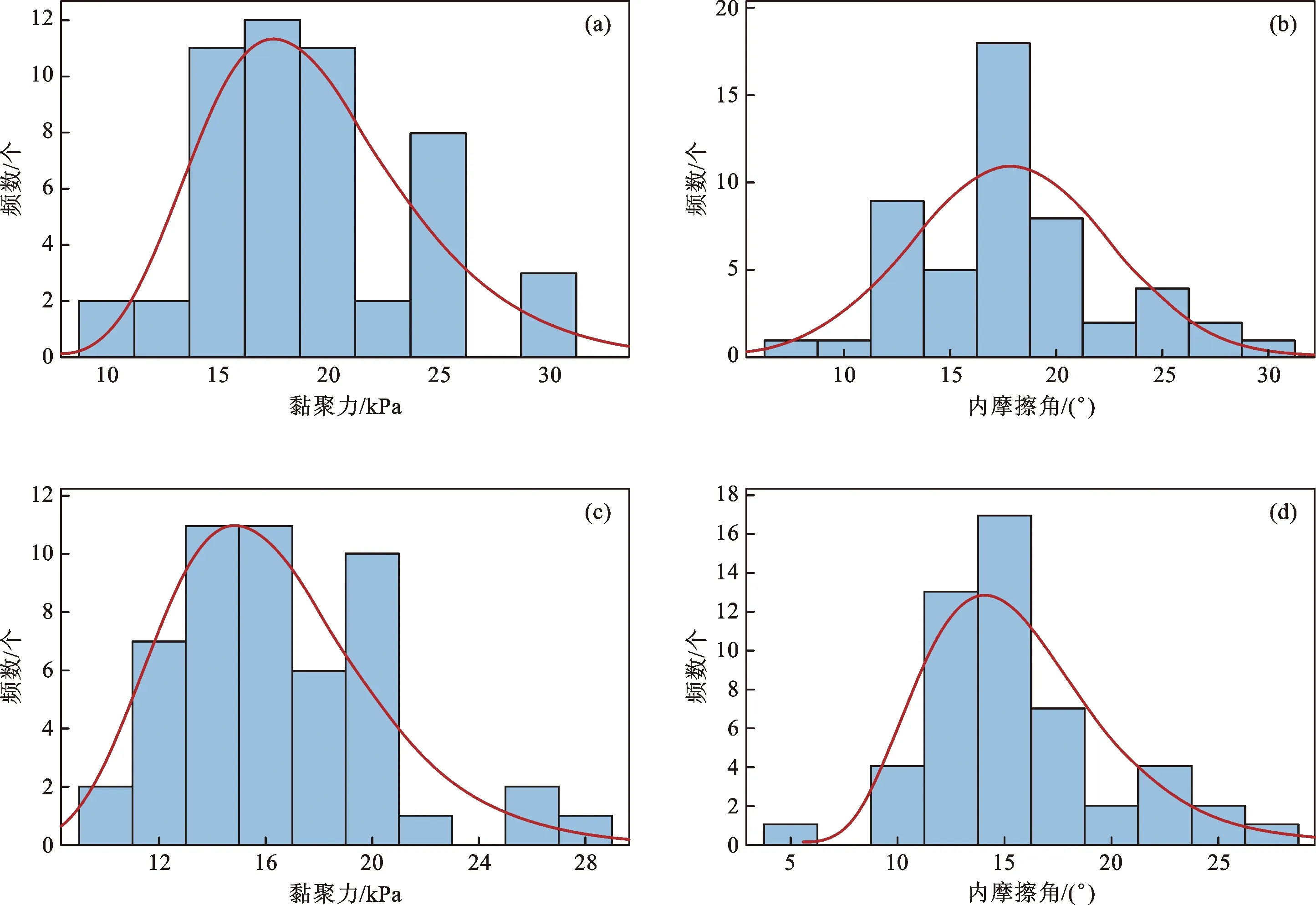
a.c1对数正态分布图;b.φ1正态分布图;c.c2对数正态分布图;d.φ2对数正态分布图

表3 滑带土抗剪强度参数c、φ取值的概率分布函数
2.2 滑带土抗剪强度参数设计值与试验值相关性研究
滑带土多埋藏在启动后的滑坡体之下一定深度内,由于时间、资金、现场条件等限制,不可能进行大量现场大型原位剪切试验。对于碎石土等物质构成的滑带土,室内试验又很难模拟滑带土实际的受力状态及变化过程,因此,室内试验数据一般不宜直接应用于滑坡稳定性评价及滑坡治理工程设计。经验公式估算方法以一定的地形地质结构特性、室内及现场试验数据为基础,通过回归等手段求出滑带土抗剪强度参数。由于滑带土影响因素的复杂性及未能引入更多的地质素描,因而应用不同的经验公式对同一滑带土强度参数进行估算时存在较大的离散性。滑动面的强度参数与滑坡发育状况、滑体的结构与组成、滑坡性质与类型、地下水等因素密切相关,因此在实际工程中,滑动面的强度参数应在室内及现场物理力学试验的基础上,结合滑坡宏观变形破坏迹象及工程经验综合确定。
目前基于实例统计得到的滑带土抗剪强度参数设计值主要是通过反演原斜坡在暴雨工况下发生破坏的临界状态计算得到的。查阅相关文献可知,当斜坡滑动以后,各类岩土的强度发生衰减,其黏聚力和内摩擦角普遍降低至峰值强度的70%~90%。徐邦栋在《滑坡分析与防治》[15]一书中指出,应选用试验强度参数值的70%作为滑坡稳定性评价的参数取值;张有天在《岩石高边坡的变形与稳定》[16]一书中指出,各类结构面的抗剪强度残余值与峰值平均值的比值为:c′/c=0.42~0.7、φ′/φ=0.60~0.85。目前大多数学者选用试验值的0.7倍作为参数取值进行滑坡稳定性分析。
本文在试验值的基础上,选取0.50~0.85的比率系数(R),分析其与设计值的相关程度,得到黄冈市片麻岩类堆积层滑坡的强度参数设计值与试验值的最优比率(表4)。

表4 设计值与不同比率试验值统计表
对比以上设计参数值与各比率下试验参数值的线性分布情况(图6)可知:天然工况下黏聚力c1的设计值线性与R为0.7、0.65、0.6、0.55的试验值线性逼近或交叉,内摩擦角φ1的设计值线性与R为0.65、0.6、0.5的试验值线性逼近或交叉;饱和工况下黏聚力c2的设计值线性与R为1的试验值线性交叉,内摩擦角φ2的设计值线性与R为0.7、0.6、0.55的试验值线性逼近或交叉。

a.c1 R值对比分析图;b.φ1 R值对比分析图;c.c2 R值对比分析图;d.φ2 R值对比分析图
综上可知,天然工况下强度参数设计值与试验值c′/c=0.55~0.7,φ′/φ=0.5~0.65;饱和工况下强度参数设计值与试验值c′/c=1,φ′/φ=0.55~0.7。因此黄冈市片麻岩类堆积层滑坡滑带土抗剪强度参数设计值与试验值的相关性总体符合相关文献中提出的经验比值,且饱和工况下的黏聚力设计值与试验值更接近。
3 结论
(1) 依据实例并运用数理统计分析,得到黄冈市片麻岩类堆积层滑坡滑带土抗剪强度参数取值区间为:天然工况下黏聚力c1为17.75~20.43 kPa,内摩擦角φ1为16.41°~19.00°;20年一遇暴雨饱和工况下黏聚力c2为14.99~17.19 kPa,内摩擦角φ2为14.42°~16.74°。天然工况下黏聚力c1、饱和工况下黏聚力c2与内摩擦角φ2的散点分布更服从对数正态分布;天然工况下内摩擦角φ1的散点分布更服从正态分布。
(2) 滑带土抗剪强度参数试验值与反演得到的设计值服从经验规律,即天然工况下强度参数设计值与试验值比值为c′/c=0.55~0.7、φ′/φ=0.5~0.65;饱和工况下强度参数设计值与试验值比值为c′/c=1、φ′/φ=0.55~0.7。可为黄冈市片麻岩类堆积层滑坡稳定性分析与防治工程设计等取值提供参考依据。
