基于小波包组合特征和LMS-LSTM 的表面肌电信号分类*

孔康，李德盈，孙中圣

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

表面肌电信号作为生物电信号的一种，由于能够反映较多的生物运动特征，被广泛应用于康复训练装置的设计和假肢控制等领域。肌电信号具有微弱性和突变性，在数据采集的过程中易受其他信号的干扰，给分类的结果带来较大影响。目前常见的分类特征主要有时域、频域和时频域。于亚萍等人[1-2]利用多种母小波变换对表面肌电信号进行识别；胡晓[3]等人利用小波包系数熵作为特征向量，但时频信号存在高延迟性。本文在小波包系数特征的基础上，添加了延迟性较低的方差特征，创新地采用将时域和时频域组合的方式作为特征参数。常见的分类器有支持向量机、随机森林和线性判别等，但这些方法的识别率会随输入向量维度的增加而下降。而近年来国内外对深度学习的研究越来越深入，此方法也被广泛地应用于信号处理领域。另外，自适应滤波(Least Mean Square，LMS)作为一种检测平稳与非平稳信号的滤波方式，被用于信号的去噪处理。本文参考长短时记忆网络(Long and Short Time Memory Network，LSTM)用于不同分类的文献[4-9]和陈景良等人[10]使用LMS 对语音进行降噪、石欣等人[11-12]利用LMS-随机森林模型对下肢动作进行分类后，综合具有较高实时性的LMS和较高识别率的LSTM 两种算法的优势，采用两种算法组合，与陈思佳等人[13]采用LSTM 和卷积神经网络得到较高手势动作识别率相比提高了实时性。

1 特征参数的提取

1.1 小波包分解系数

采用小波包变化提取表面肌电信号的时频特征，利用小波包变换将肌电信号同时进行高频和低频的多层次分解，弥补了小波变换随分解层数的增加对高频部分分解不足的缺点[14-15]。由于表面肌电信号的频率范围主要在10～150 Hz，因此采样频率选择320 Hz，对应奈奎斯特采样频率为160 Hz，通过提取0～160 Hz 的频段信号可以有效滤除其他干扰。本文选择具有较快收敛速度的Meyer 小波基，做i 层小波包分解。进行i 层分解后，最后一层共有2i个频带，即可将160 Hz 信号i 等分，每个频带对应的频率范围为160/i Hz，从左到右递增排列。小波包系数是小波包分解后每个子空间的系数，整个空间频带的小波包系数可构成矩阵[3]：

其中，k 为每个频带小波包系数长度。取小波包系数为特征值，共可取2i个特征值，每个特征值有k 条数据,d2i，k表示第2i个小波包系数特征的第k 条数据，所有数据组成特征矩阵Dm。文中选取i=3，k=1 585，可形成一个8×1 585 的时频特征矩阵。

1.2 方差

作为区别表面肌电信号的一种时域特征，方差表示活动段肌电信号的功率，计算公式如下：

其中，N 表示肌电信号个数，yt表示第t 个肌电信号，VARj表示第j 个窗口的方差。

方差与平均绝对值、均方根等常被用作分类特征。本文在对方差、平均绝对值、均方根、过零点数等特征进行LMS 算法滤波处理过后，发现方差特征具有良好的区别效果，故删去其他时域特征。由于肌电信号存在突变性，本文在处理方差特征值时采用重叠分割的移动窗口法，使窗口每次滑移的增量小于窗口宽度。考虑窗口宽度和滑移量过小，计算易受信号突变的干扰，过大又不能精确反映动作间的区别，本文在多次尝试之后，选择窗口宽度为8 ms，移动增量为4 ms。

2 LMS 降噪处理

自适应滤波器(LMS)可以在没有关于待提取信息的先验统计知识下直接利用观测数据，依据某种判据在观测过程中不断递归更新处理参数，逐步逼近某一最优的处理效果。即迭代计算调节滤波器参数W，使目标函数et最小。计算步骤如下：

(1)设横向自适应数字滤波器的输入为xt，理想输入为dt，实际输出为yt，滤波器初始参数W=0，假设et、dt和xt统计平稳。本文构造一个均值为0、方差为1 的高斯白噪声和数字频率为0.05、信噪比SNR 为1 的正弦信号作为理想输入dt。

(2)滤波器输出估计值：

其中，Wt，m表示第t 个采样点第m 个权系数；xt-m表示第t-m 个信号。

(3)计算估计误差：

(4)利用迭代公式更新下一时刻权值：

其中，u 为学习率，取0.05。

3 LSTM 网络分类器

长短时记忆网络(LSTM)是基于循环神经网络RNN只有一个隐藏层状态h(t)的改进，即通过添加细胞状态C(t)用于保存长期状态，解决学习序列数据的时间步之间的长期依存问题，适用于动态数据的分类。通过引入“门”的概念控制细胞状态C(t)，包括遗忘门、输入门和输出门。其中遗忘门用于决定上一时刻的细胞状态C(t-1)保留当前时刻C(t)的值，调节取值范围(0，1)来表示遗忘程度[13]，0 表示全部遗忘，1 表示全部记住。输入门控制当前网络的输入X(t)保存到细胞状态C(t)的值，输出门控制C(t)输入到当前输出量的值h(t)。具体公式如下：

遗忘门：

输入门：

激活函数输出：

细胞状态：

输出门：

其中，σg为门激活sigmoid 函数，W 和b 分别表示权重和偏倚量，X(t)表示第t 个输入，tanh 为激活函数。本文最大轮次取100，学习率为0.001，批大小为32，隐藏单元数目为20。LSTM 算法框图如图1 所示。

4 实验与结果分析

4.1 实验数据采集

本文的研究目标是实现屈拇指、屈中指、屈无名指和小指、握拳、屈腕5 种手势动作的区分。在参考了各手势动作所对应的前臂肌肉肌群共涉及拇长屈肌、指浅屈肌、指深屈肌和尺侧腕屈肌4 个肌群后，设计1 000 Hz采集频率的四通道采集电路。

采集装置选择电极材料为Ag 的一次性按扣式贴片。实验者为21 岁健康男性，身高为181 cm，体重为74 kg，采集实验时依次保持手势动作2 s，恢复放松状态保持2 s，共计40 s，每种动作完成10次，共40 000 条数据。采集手势动作如图2 所示。

4.2 滤波处理

将采集到的表面肌电信号依次通过2 个截止频率为20 Hz 的高通滤波器，阻带频率为45 Hz、通频带频率为52 Hz 的陷波器，以及2 个截止频率为500 Hz 的低通滤波器，完成初步的信号滤波处理。

使用窗口能量法划分活动段，选取长度为4 ms 的窗口，采用窗口段内肌电信号数值的平方值代替该段窗口的能量，通过多通道累加计数的方式，当存在两个通道以上数量的窗口大于初始设定的阈值，即认为该窗口段为活动段。实验中阈值选择无窗口段能量的1.4倍，为0.003 6 μV2。考虑到部分手势信号可能存在幅值低而被误作非活动段，因此仅取活动段信号的前11 980 条数据。

使用LMS 算法对采集信号进行二次降噪处理，处理结果如图3 所示。

4.3 输入特征样本

将经LMS 处理后的信号通过方差计算，每种手势动作得到4×2 394 个方差特征值。另将信号通过小波包变换，提取小波包系数特征。实验发现经LMS 算法处理后的信号提取的方差特征对分类效果有所提高，但小波包系数特征对分类效果反而降低。因此，本文仅对方差特征运用LMS 滤波处理，小波包系数只通过滤波器处理。不同滤波处理方式处理不同特征的分类结果如表1 所示。

表1 滤波处理方式对比(%)

每个动作每个通道得到8×1 585 个小波包系数特征值。利用同一手势动作的肌电信号的特征具有相关性且时域特征具有重复性，因此方差特征取前1 585 条数据，5 个动作共得到7 925 条数据，每条数据由一个36 维特征矩阵组成。取其中4 755 条数据为训练样本，剩下为测试样本。为区分不同动作，给每个动作设定一个标签，屈拇指为标签1、屈中指为标签2、屈无名指和小指为标签3、握拳为标签4、屈腕为标签5。同样得到7 925 条标签数据，构成标签矩阵，与输入样本一样分成4 755 条训练样本标签和3 170 条测试样本标签。

将数据代入LSTM 分类模型中，得到5 种动作的平均识别率为93.78%。计算过程如图4 所示。

采用不同分类器和不同分类特征得到的分类结果如表2 所示。

表2 不同特征和分类器分类结果对比

4.4 PCA 优化模型

考虑到每个动作的输入特征为36维，极大地造成了识别的延迟性。通过主成分分析的方式对输入特征向量进行降维，减少识别反应时间。

计算过程如下：

(1)36 个特征值、7 925 条数据可构建样本矩阵，标准化处理后得到矩阵X：

其中，N3为提取特征后的信号个数，即7 925；p 为特征维度，即36。

(2)计算X 矩阵的协方差矩阵：

(3)计算R 的特征值和特征向量，以及累计贡献率：

其中，λm表示每阶的贡献率。

(4)一般取累计贡献率达到80%时的特征值对应最终主成分：本文当主成分阶数为24时，累计贡献率达91.15%，使用降维后的数据，组成新的输入矩阵代入LSTM 模型，得到表3 结果。

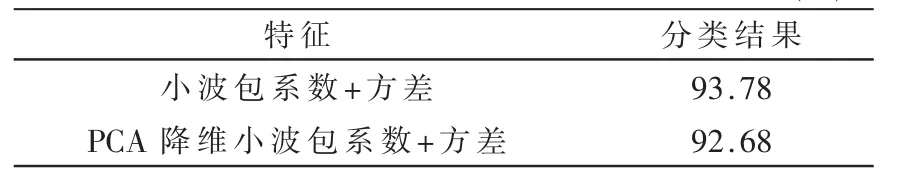
表3 降维前后分类结果对比 (%)

5 结论

本文提出了LSTM 深度学习的分类器，在一次滤波的同时，创新结合LMS 滤波算法，对方差特征进行二次滤波，得到了更高的分类识别率。通过采用小波包系数和方差的组合特征作为分类输入特征，对屈拇指、屈中指、屈无名指和小指、握拳、屈腕5 种手势动作进行离线识别的分类，得到93.78%的平均识别率。对比线性判别和决策树分类结果，LSTM 算法具有很高的正确性。使用PCA 降维后特征向量维数从36 变为24，识别率达92.68%，实现了优化的目标。