基于智能手机测量液体黏滞系数的方法研究

曲 阳,曹显莹，曹国军，何海霞

(哈尔滨石油学院，黑龙江 哈尔滨 150000)

液体的黏滞系数又称为内摩擦系数或粘度，是描述液体内摩擦力性质的一个重要物理量。它是表征液体反抗形变能力的重要参数，液体黏滞系数的测量在生产生活、化学化工、工程技术、医疗和国防等众多领域有着广泛的应用价值[1]。

研究者经过几十年的努力，研究出多种黏滞系数的测量方法，如毛细管法、旋转法、落球法及振动法等[2]。其中，落球法是最常见、最基本的一种方法，该方法物理现象明显、原理简单、实验操作方便，作为经典实验被广泛应用于各大高校的大学物理实验的教学[3]。但这种黏滞系数的测量方法依然存在一些不足，如金属球在下落过程中难以对准激光导致计时器不计时，以及金属球的重复利用和实验液体污染等问题。为了解决这些问题，实验者们除了对实验设备进行改进之外[4-6]，也提出来一些新的测量方法，如强迫振动扭转法、阻尼振动法等[7,8]。

随着信息时代科学技术的发展，智能手机的功能越来越强大，人们可以通过智能手机的各种传感器完成数据的采集、运算以及分析等各项工作。基于上述优点，近年来，利用智能手机上搭载的先进软件硬件设备进行物理实验的探究成为普遍趋势，越来越多的物理教师把智能手机作为实验教学的新型仪器应用到物理实验设计中[9,10]，从而更好地进行物理实验教学，这也是对传统物理实验教学方法的一种创新。

本文提出利用智能手机来实现液体黏滞系数的测量方法，利用智能手机中的加速度传感器采集弹簧振子的加速度数据，通过阻尼振动的动力学方程计算出金属球做阻尼振动时液体的阻尼系数和黏滞系数。与传统方案相比，基于智能手机的液体黏滞系数测量方法操作简单且趣味性强，充分调动了学生的积极性和创造性，从而提高了学生的实践动手能力，同时降低了传统实验方法的仪器成本，对物理实验的线上教学具有一定的参考意义。

1 实验原理

阻尼振动是由于振动系统受到摩擦力或介质阻力或其他能耗而使振幅随时间逐渐衰减的振动。如图1所示，智能手机分别与弹簧和金属球相连，将金属球浸入到溶液中，让其进行阻尼振动，由于黏滞阻力使得金属球的振幅逐渐减小，能量逐渐消耗。液体中的金属球可视为弹簧振子，对弹簧振子进行受力分析有。

m球g-F浮=kb-m手机g

(1)

其中b为弹簧振子向下移动的距离。

图1 小球受力图

当弹簧振子在油或者液体中作阻尼振动时所产生的黏滞阻力与其运动速度成正比，弹簧振子运动的越快，产生的黏滞阻力越大，黏滞阻力可表示为

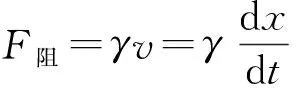
(2)

因此弹簧振子在坐标X处时，有

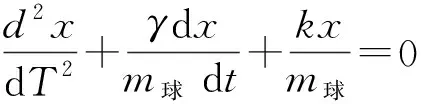
(3)

(4)

其中，β是阻尼系数，ω0为系统的固有角频率。该动力学方程式的通解为

(5)

此时，振动周期为

(6)

其中，ω是阻尼振动时的角频率，可得

(7)

由式(7)和β=γ/2m球的关系式可得，

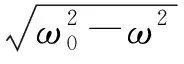
(8)

弹簧振子所受黏滞阻力为

f=6πηrv

(9)

式(9)和(3)可得

(10)

可见，只要测量出金属球无阻尼振动时的固有角频率ω0、阻尼振动时的角频率ω、金属球的质量m和半径r，即可计算出液体的黏滞系数η。

2 实验方法

2.1 实验器材及原理

实验装置如图2所示，其中包括弹簧、智能手机、金属球、硅油、甘油、不透明溶液、支架等实验仪器。将弹簧、智能手机和金属球按图2所示的顺序进行安装，利用智能手机的加速度传感器测量金属球阻尼振动和无阻尼振动时的a-t曲线。

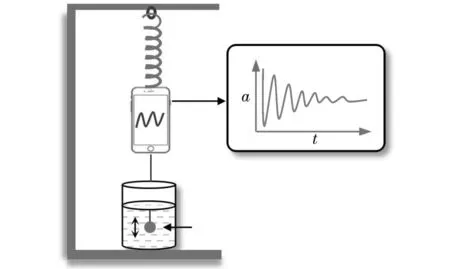
图2 实验装置示意图

2.2 实验步骤

(1)实验按照图2连接实验装置，选取适当劲度系数的弹簧，将弹簧固定在支架上。将智能手机固定在弹簧下端，用长10 cm的细线将手机与金属球相连，此时金属球视为弹簧振子。实验中，选取不同质量和半径的金属球，分别观察它们的加速度变化曲线。

(2)打开智能手机中的加速度传感器，测量弹簧振子在空气中和液体中的加速度变化曲线。

(3)测试无阻尼时的振动曲线。让弹簧振子在空气中振动，通过加速度传感器测量弹簧振子做无阻尼振动时的加速度曲线，通过傅里叶变换得到弹簧振子的频率F0，通过公式ω0=2πF0，计算得到固有角频率ω0，并记录实验数据。

(4)测试有阻尼时的振动曲线。在室温(21 ℃)时，将硅油装入大口径烧杯中，将烧杯放置在实验平台上，调节烧杯的位置，保证弹簧振子沿着中心轴线运动。调节烧杯的高度，使弹簧振子在溶液中的适当位置。让弹簧振子在液体中振动，打开加速度传感器测量弹簧振子进行阻尼振动时的加速度，通过傅里叶变换得到弹簧振子的频率f，通过公式计算得到角频率ω，并记录实验数据。

3 数据处理及分析

图3为用Origin数据处理软件所做的弹簧振子的a-t曲线，从图中可以看出弹簧振子的振幅基本不变，说明弹簧振子受到的空气阻尼很小，可视为无阻尼振动。对振动曲线进行傅里叶变换求解，计算出无阻尼时弹簧振子的频率F0，利用ω0=2πF0公式，得到弹簧振子的固有角频率ω0=8.569 rad/s。

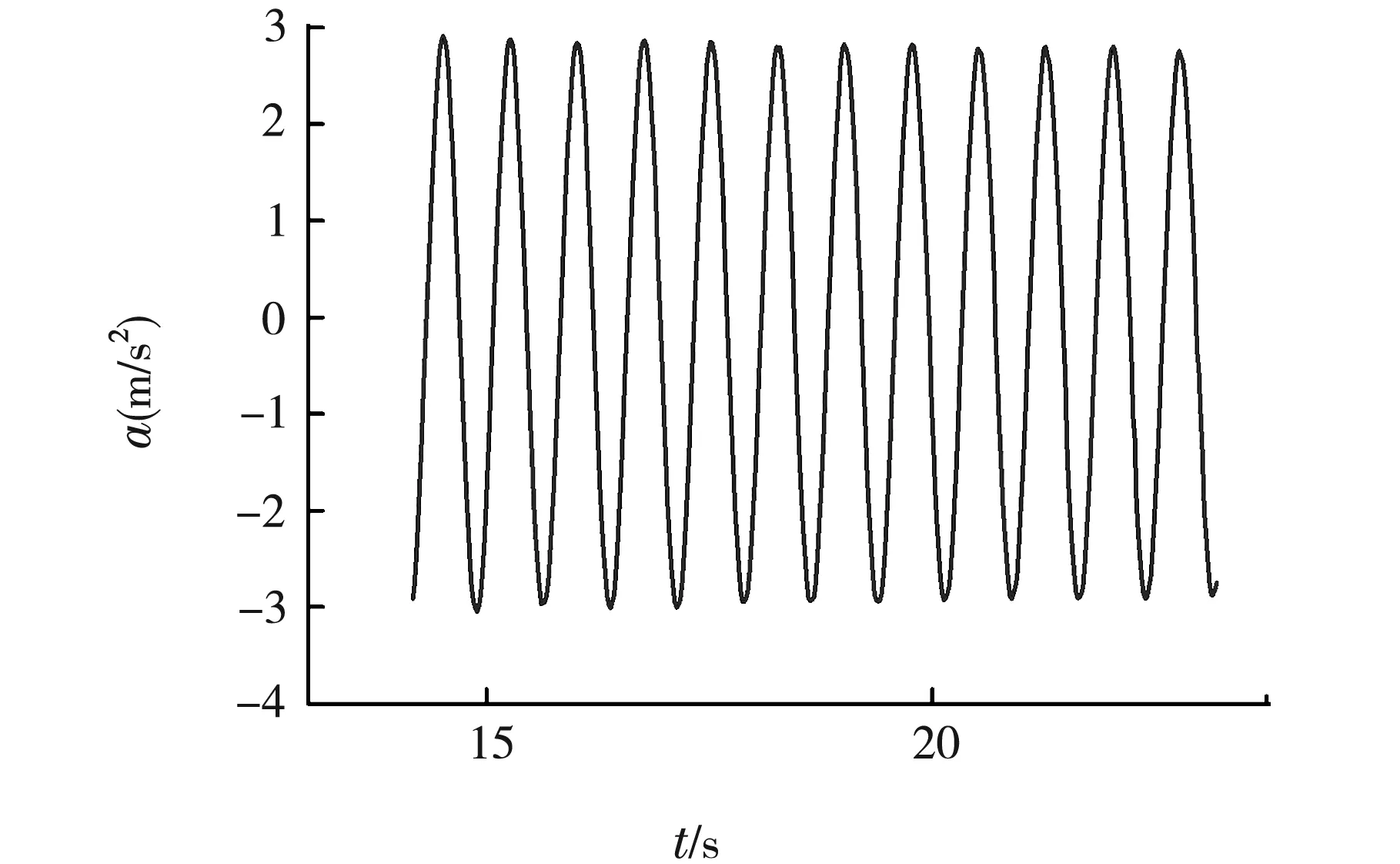
图3 弹簧振子无阻尼振动的a-t曲线

图4为阻尼振动时弹簧振子的a-t曲线，由于黏滞阻力的作用，弹簧振子的振幅不断随时间衰减，系统能量不断损失，说明弹簧振子在作阻尼振动。同样对a-t曲线进行傅里叶变换，得到弹簧振子的角频率ω=8.168 rad/s。

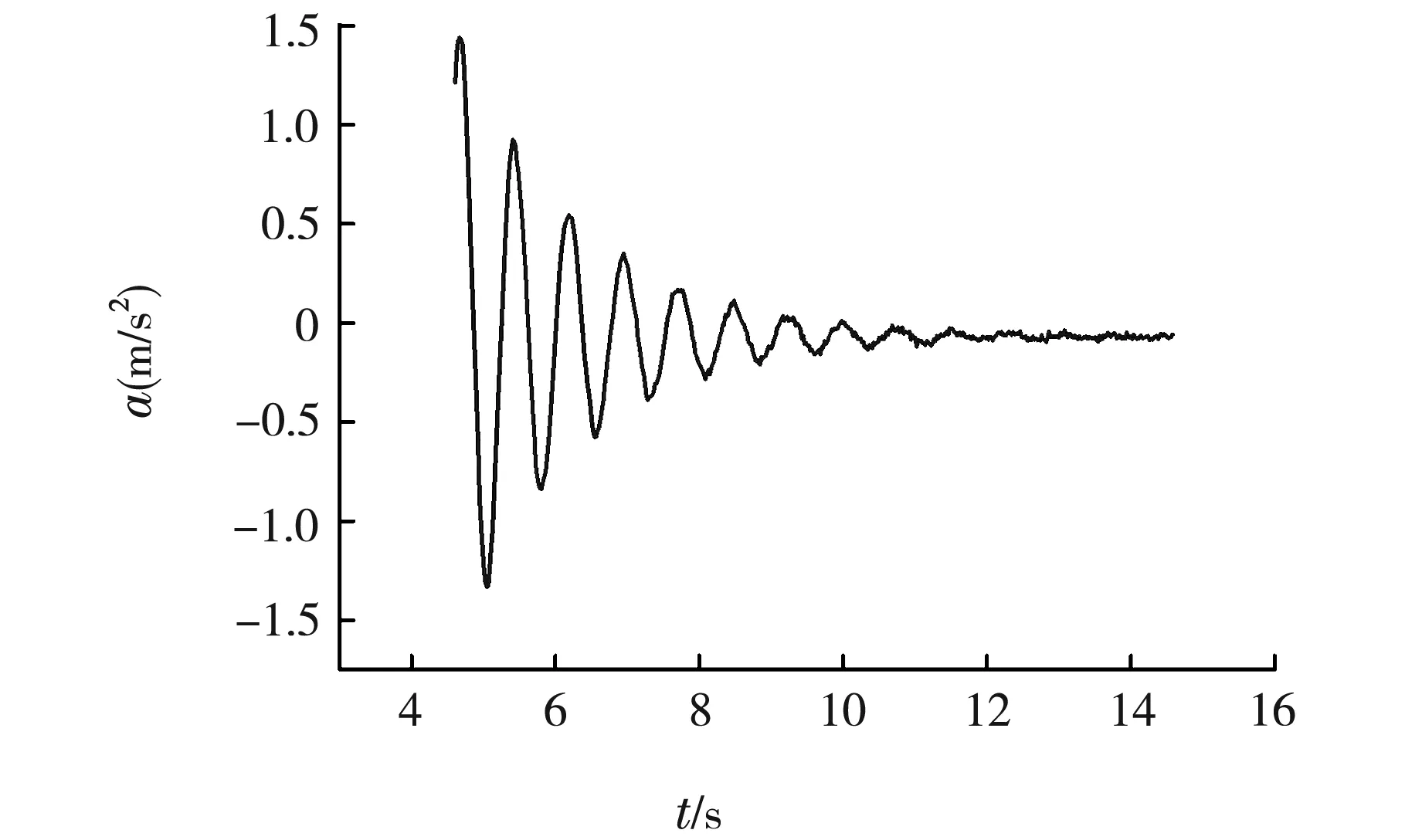
图4 弹簧振子阻尼振动的a-t曲线

将ω0、ω、m球以及r代入到公式(10)中，即可计算出硅油的阻尼系数β=2.588 Ns/m，黏滞系数η=0.6465 Pa·s。与文献[11]给出的21 ℃时硅油的黏滞系数为0.644 Pa·s，进行比较，其相对误差为0.39%。

为了验证该实验方案的可行性，本文同时对甘油及不透明液体进行了黏滞系数的测量，如表1所示，对于甘油的黏滞系数，两组测量值相差不大，与真值比较时，相对误差仅为3%。对于不透明液体的黏滞系数，两组的测量值相差过大，这可能是由于液体的黏滞系数较小且液体不透明，导致小球下落过程太快，光电门无法精确感应到金属球的位置，从而导致测量的数据与真值相差过大。

表1 不同溶液的黏滞系数的数据表

表2是不同质量弹簧振子黏滞系数的测量值，可以看出随着弹簧振子质量的增加，黏滞系数逐渐增加。当m=20g时，测量值更接近于真值。这是因为黏滞阻力与m成正比，m越大，黏滞阻力越大，而角频率越小，从而使得计算出的黏滞系数越大。因此，选取适当的弹簧振子是本实验的关键。

表2 不同质量弹簧振子测得的液体黏滞系数的数据表

4 结 语

本文基于阻尼振动原理，利用智能手机测量弹簧振子的加速度，通过阻尼振动的动力学方程通解计算出金属球做阻尼振动时液体的阻尼系数和黏滞系数，并将黏滞系数测量值与理论值进行比较，相对误差为0.39%。为了进一步论证了本实验方案的可行性，又分别测量了两种不同液体的黏滞系数，我们发现对于黏滞系数较小的溶液，本实验方案更加接近于真值，进一步论证了本实验方案的可行性。与传统方案相比，基于智能手机的液体黏滞系数测量方法操作简单且不受空间和时间的限定，同时降低了传统实验方法的仪器成本，对学生开展设计性实验、创新实验及居家实验具有一定的参考意义。