无限长双曲柱面导体间电场的分布

张忠东

(内蒙古兴安职业技术学院，内蒙古 乌兰浩特 137400)

在一般的电磁教材中，讨论了无限大的带电导体平板间、两导体球间、两导体圆筒间的电场问题。文献[1-3]利用保角变换和电像法、椭圆柱面坐标、解析函数法讨论了无限非同轴圆筒、无限长共焦椭圆柱面间的电场问题；文献[4]用Matlab进行数值模拟了带电椭球体等势线和电场线的空间分布。本文利用解析函数的性质，推导电势与电场强度的分布函数，通过满足拉普拉斯方程的电势函数，得到等势线和电场线方程，并利用Matlab绘出电场线和等势线分布图。

1 无限长双曲面及共焦等势线方程

两个无限长带电双曲柱面导体，垂直于z轴平面与双曲柱面相截,得的是双曲线M和N，由于无限长带电双曲柱面导体在空间产生的电场分布与z轴方向无关，可作为平面场问题进行分析，取其横截面，建立图1所示坐标系。

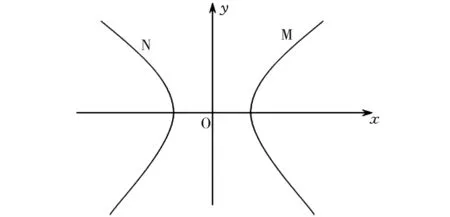
图1 带电双曲柱面截面图

图1中带电双曲柱面导体截面双曲线方程为：

(1)

两支分别为：x>0为M支曲线，x<0为N支曲线，焦距c2=a2+b2。由电场的分布特点可知，其等势线与上述带电双曲柱面共焦，共焦方程可表示为：

(2)

式中cos2ξ、sin2ξ取不同的数值，可得到不同的共焦双曲线。由方程(2)解得：

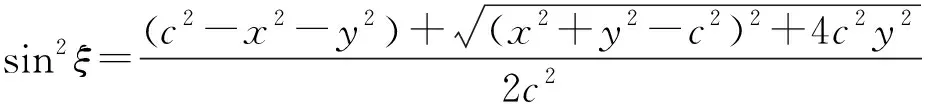
(3)

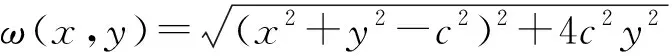
(4)

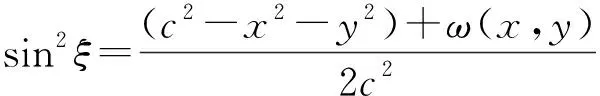
(5)

2 电势分布函数及等势线方程

如果将电势分布函数看作是某解析函数f(x,y)=u(x,y)+iv(x,y)的实部u(x,y)，则函数u(x,y)一定是调和函数，令电势分布函数u(x,y)等于任意常数，就可得到等势线方程。

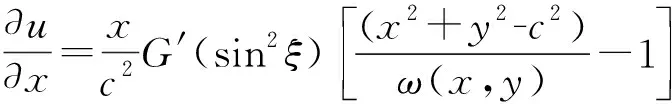
(6)

由(6)式得：

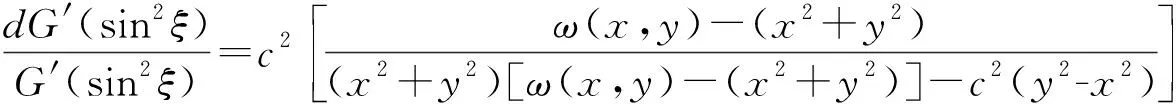
(7)

由(2)、(4)、(5)、(7)得

(8)

(8)式积分得

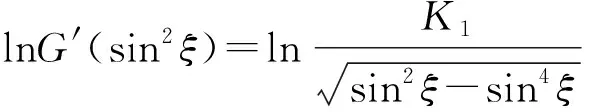
(9)

(9)式积分得

G(sin2ξ)=K1arcsin[2sin2ξ-1]+K2

(10)

由(3)、(10)得

(11)

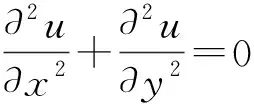
即带电双曲柱面导体间电势分布函数为：

(12)

由边界条件确定K1、K2两个常数：设导体面M上的电势为u1，导体面N上的电势为u2，且u1>u2。由于M导体面是等势面，在M上取x=a、y=0点，其电势为u1。

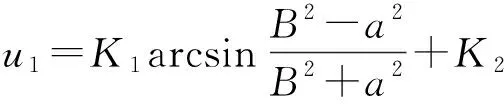
(13)

由于N导体面是等势面，在N上取x=-a、y=0点，其电势为u2。

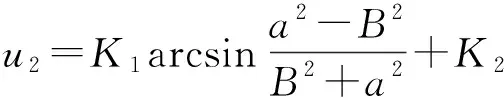
(14)

(15)

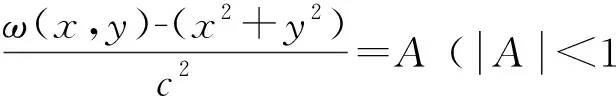
(16)

式(16)为双曲柱面导体间电场的等势线方程，通过取不同的A值可得到等势线为共焦双曲线族。

3 电场强度分布函数及电场线方程

由E=-∇u，可得到双曲柱面导体间电场强度的分布：

(17)

(18)

根据解析函数的实部函数与虚部函数对应的曲线族在空间处处正交的性质，若将u(x,y)作为解析函数的实部，通过上述构造的解析函数f(x,y)求其虚部v(x,y)，即可得到电场线方程。

(19)

令式(19)中的v(x,y)等于任意常数，即

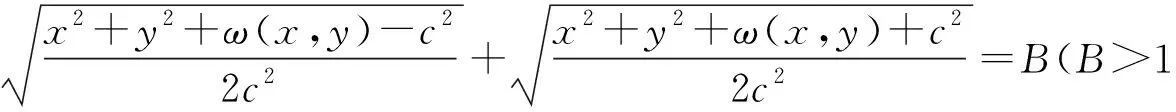
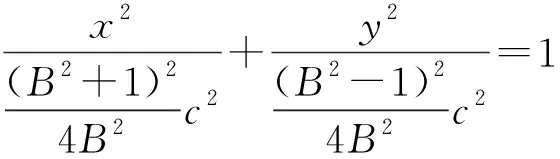
(20)

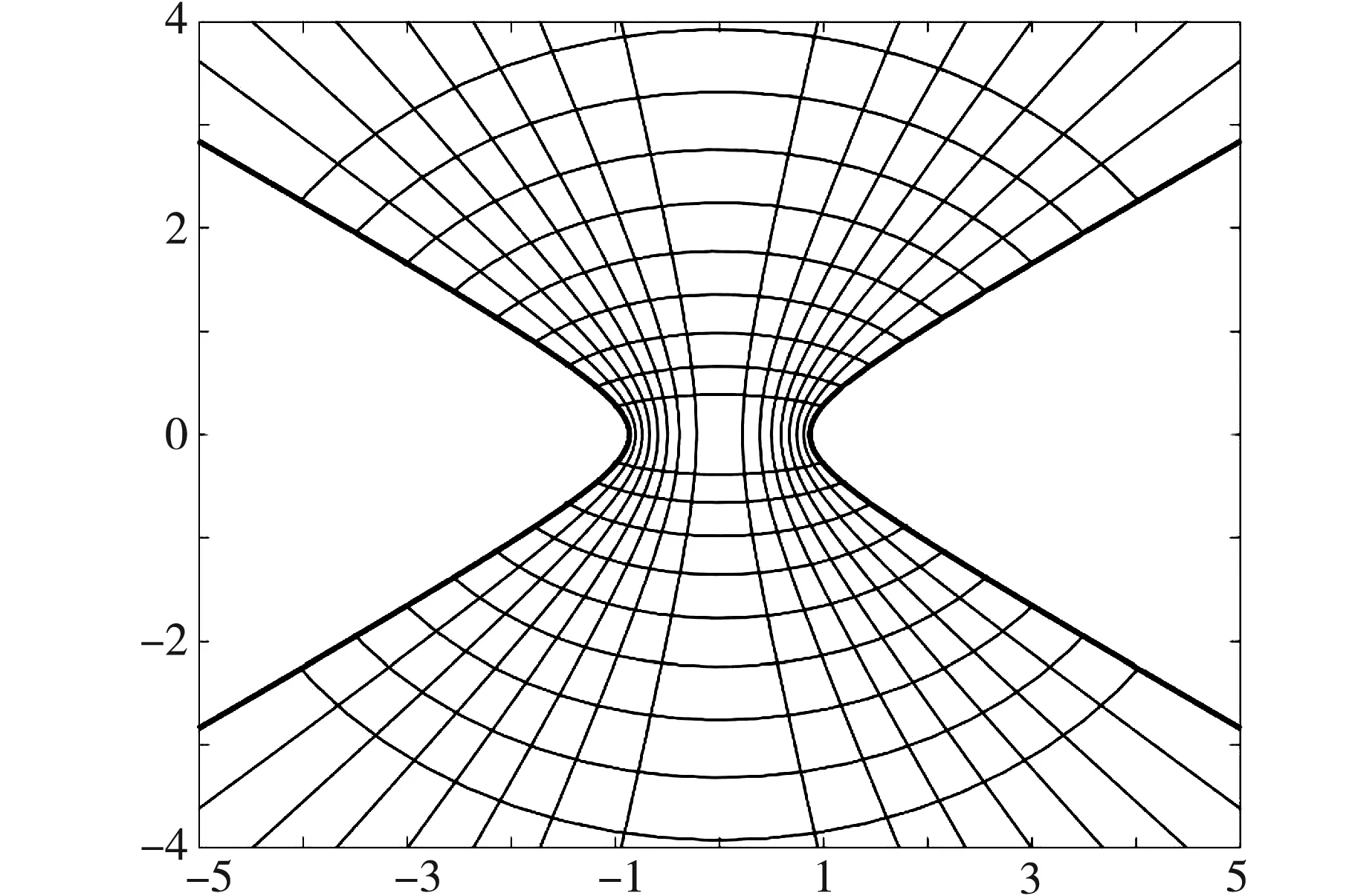
图2 等势线与电场线分布

式(20)为双曲柱面导体间的电场线方程，通过取不同的B值可得到电场线为共焦椭圆曲线族。在式(16)、(20)中，常数A、B取不同数值，利用Matlab软件，绘出了等势线和电场线图线(见图2)。

4 结 语

本文利用解析函数求出了直角坐标表示的双曲柱面导体间的电势和电场强度分布函数，得到了等势线和电场线方程。根据等势线、电场线方程，利用Matlab软件，绘出了等势线和电场线图线，验证了它们为共焦的双曲线族和椭圆族，在教学上具有一定的理论意义和实用价值。