基于图像识别技术的弹簧摆动力学实验研究

董雨萱，余家辉，叶晓阳，郑晓秋，李炳伟

(杭州师范大学 物理学院，江苏 杭州 311121 )

自然和社会系统是一类典型的非线性复杂系统，有着丰富的动力学行为。 最近几十年来，非线性动力学及相关概念已经潜移默化地融入到生活中的各个方面，如萤火虫同步、天气预报、金融市场中的股市等[1]。 因此，研究非线性系统的各种动力学行为对于认识自然和社会具有重要作用。 力学系统中有许多经典的非线性系统，如弹簧摆(又叫弹性摆，见图1左)，虽然其结构简单，但其动力学非常丰富，除了周期运动，还有准周期、混沌以及内共振等现象，是理论和实验研究非线性动力学的常用模型。 此外，弹簧摆在实际工程中也有重要而广泛的应用。

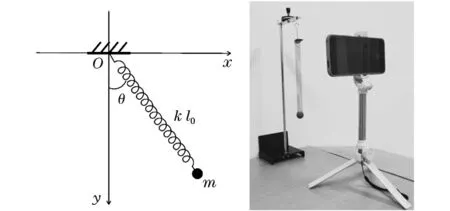
图1 弹簧摆模型示意图(左)和实验装置图(右)

目前大部分学者运用理论和数值计算的方法探讨了弹簧摆的运动。 例如，杨正波[2]、管慧[3]等人从理论上研究了在不同参数控制下受稳定约束弹簧摆的运动行为；张义灵等人从数值上探讨了弹簧摆内共振和混沌现象[4]。 不同于单摆，弹簧摆动力学相当复杂，在实验上如何记录数据是一个很大的挑战。因此，从实验角度对弹簧摆的动力学行为的研究很少。 随着科技进步和社会发展，特别是智能手机的普及使得记录物体的运动变得极其简单。 结合相关软件的发展，使得人们能够识别并分析物体的长时间运动。 近些年来，越来越多的图像识别软件或程序成为物理实验室中流行的一种分析工具[5-11]。 例如，王昭等人使用Tracker软件进行目标物的追踪和分析，实验上对有摆线弹簧摆动力学进行研究[5]；黄膺达借助OpenCV库函数识别视频中的单摆，得到了单摆的周期和重力加速度[8]；闫彩霞利用Tracker软件分析两个小车在弹性碰撞和完全非弹性碰撞过程中系统动量随时间的变化情况[9]。 此外，Loo Kang Wee通过研究发现，与被动的、非互动的传统物理课程相比，运用视频分析技术和图像识别技术能帮助学生更好地理解运动背后的物理原理并扩大课程的教育影响[10]。

基于上述背景，在实验上通过智能手机记录弹簧摆运动的视频，然后基于Matlab图像识别技术探讨了在不同实验条件下的弹簧摆的动力学行为。 利用功率谱和最大李雅普诺夫指数对动力学行为进行分析和定量刻画。

1 实验装置

弹簧摆由劲度系数为k，原长为l0的轻质弹簧和质量为m，直径为d的小球构成。 为便于实现对摆球的识别，实验上小球表面涂抹蓝色颜料。 弹簧摆一端悬挂于铁架台O点，智能手机摄像头对准目标物，进行连续曝光或拍摄视频，见图1。 期间保证拍摄平面与小球运动平面平行，且不考虑弹簧扭转变形等。

2 动力学方程

根据图1(左)所建立的坐标系，在任意时刻，系统的动能T为[2]

(1)

其中，m为小球质量。以O点为重力势能零点，弹簧自由伸长时为弹性势能零点，系统的势能为

(2)

在(2)式中，l=l0+d/2，则拉格朗日函数为

(3)

将此物理系统的运动以拉格朗日运动方程表示为

(4)

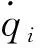
(5)

(6)

在极坐标系下表示为，

(7)

(8)

3 实验操作和影像分析

实验中使用的智能手机为HONOR9X，其相机型号为索尼IMX582。 曝光时间和视频帧率分别为1/500s和30fps。 为了平衡信息的准确性和计算成本，实验选择的像素窗口大小为1 280×720。

首先，打开相机水平仪，调节相机位置使得屏幕中的横向和竖向参考线分别与图1所示坐标系的x轴和y轴平行。 调试完毕后录制物体运动视频，得到一系列包含物体运动信息的连续图像，如图2所示。

图2 弹簧摆连续曝光图像(部分)

接着，将连续图像导入Matlab软件对运动物体进行自动跟踪识别。 数字图像在Matlab中一般表达为3D实数矩阵。 每一像素点拥有特定的矩阵行列坐标(x,y)及该点的值f(x,y)[12]。 像素坐标可用于确定相对位置和测量像素间距。 灰度值表达图像信息，是进行图像操作的依据。 由于本实验中目标物与背景在图像中占据不同的灰度范围，因此采用的是以阈值分割为主的图像识别技术，识别后小球的运动轨迹如图3所示(部分)。

图3 识别后的小球运动轨迹(部分)

最后，将识别得到的像素坐标(x′,y′)按一定的函数关系转换为不易直接测量得到的空间位置坐标(x,y)，比如某直径为3.000cm的摆球在图像中测得的直径为117像素。 由此可知，物体在图像中经过一像素的距离相当于在实际空间中运动的距离约为0.026cm。 根据上述转换关系，图4显示了摆球在实际空间中的位置坐标。 上述实验操作体现了转换测量法的思想，这使得在实验室中研究非线性系统的复杂动力学行为成为可能。

3 结果及分析

通过上述实验操作和影像分析，参数为k=4.50N/m，m=30.00g，l=6.80cm的弹簧摆由θ0=28.6°静止释放后，其运动轨迹如图5所示。 设弹簧摆径向和横向的固有频率分别为ωs和ωp，两者之比记为λ，有，

(9)

研究发现，弹簧摆的运动可以分解成径向弹簧模态的振动和横向单摆模态的摆动。

图4 位置坐标散点图(部分)

图5 实际运动轨迹

图7和图8分别表示λ=1.43和λ=1.77两种条件下弹簧摆在实际运动过程中的径向、横向时序图和相图。 从图中可以看到，径向运动要比横向运动更加复杂与不规则。

(a)横向时序图

(a)横向时序图

为了更好的分析它们的动力学性质，引入在非线性时间序列分析中重要的两个工具[13]：功率谱和最大李雅普诺夫指数。 功率谱是研究时间序列的常用工具，常用于辨别时间序列是周期还是非周期的，基于信号的傅里叶变换得到。 对于一个周期的时间序列或信号，其功率谱呈现在基频单峰或谐频多峰；而对于非周期信号，其功率谱会出现一定的宽度。 最大李雅普诺夫指数这是度量轨道的发散程度，最大李雅普诺夫指数为正的，其行为意味着混沌性质；零则与周期运动相联系。 在数值计算中，利用Matlab中的内部指令FFT来计算实验上所获得的时间序列的功率谱；而对于离散时间序列的李雅普诺夫指数，采用Wolf算法[14]。在图9和图10中分别给出了λ=1.43和λ=1.77这两种情况下，横向和径向的功率谱以及李雅普诺夫指数随时间的演化。

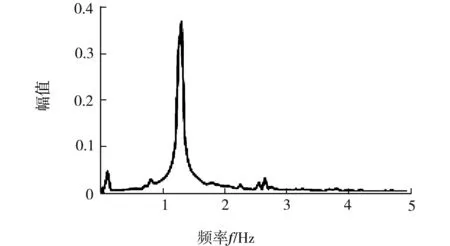
(a) 横向功率谱图

(a) 横向功率谱图

对于λ=1.43的情况下，对于横向运动发现其功率谱是个典型单峰，说明其运动具有周期性而且近似简谐运动；对于径向，功率谱出现双峰，说明是二周期的行为。 对于该参数，响应的李雅普诺夫指数非常接近零，说明系统在横向和径向的运动都是非混沌的。

接下来，对于λ=1.77的情况下，对于横向，与前面的情况类似，功率谱呈现单峰，其时间序列相对应的李雅普诺夫指数几乎为零，说明做良好的周期运动，而且是简谐的；但对于径向，其功率谱呈现一定的宽度，具有非周期的行为特征。 进一步根据李雅普诺夫指数，其值略大于零(约为0.45)，因而具有弱混沌的性质。 综合时序图、相图、功率谱图和李雅普诺夫指数图的结果可知：在实验环境下，λ=1.43和λ=1.77的弹簧摆在横向做周期运动，对于径向的运动，前者参数下做二周期的运动，后者参数下则显示弱混沌的行为。

5 结 语

基于Matlab图像识别技术实验研究了的两种参数下的弹簧摆的运动，并利用功率谱和最大李雅普诺夫指数对实验上获得数据进行分析和刻画。我们的研究表明，在两种不同的参数下，横向运动呈现出典型的周期运动，但在径向运动中略有不同。对于λ=1.43的参数下，径向仍然保持周期运动，但略微偏离简谐振动，相应的功率谱出现双峰而李雅普诺夫指数非常接近于零；对于λ=1.77的情况，径向运动的功率谱呈现出一定的宽度分布，其相应的最大李雅普诺夫指数略大于零，说明具有一定的混沌性质。

随着电脑和智能手机在学生中普及，学生们获得图像和视频等数据变得越来越简单。 利用这些工具，可以分析和完成以前难以完成的实验数据的采集和分析。 笔者认为，利用计算机分析已有的实验数据将是未来大学物理实验的一个重要的方向，是物理系及相应的专业学生所应该具有的基本技能。从这个角度上讲，本文提供了数字化大学物理实验的一个很好的范例。