基于角度传感技术的杨氏模量实验仪研制

李鹏宇,胡翠莹，高洪悦，姚金林，张少梅,张进娟，刘维慧,苗永平

(山东科技大学 物理实验中心，山东 青岛 266590 )

杨氏弹性模量(简称杨氏模量)是描述固体材料抗形变能力的重要物理量，是机械构建材料的重要参数，是工程选材的重要依据[1]。因此，在大学物理实验中为普通本科学生，特别是材料、力学等等相关工科专业，开设杨氏模量测量实验，具有重要的实践意义。

各大高校及实验仪器制造企业对杨氏模量实验及仪器进行了充分研究和改进，有力地促进了实验教学开展。段阳等概括了杨氏模量测量实验的4大类测量方法，包括静态拉伸法、动态共振法、梁弯曲法、超声波测量法，并对每类测量方法及其测量精度进行了研究分析[2]。赵杰等提出了基于莫尔条纹的金属丝杨氏模量测量方案[3,4]。姜悦等提出了基于迈克耳孙干涉仪与线阵CCD的金属丝杨氏模量测量方案[5]。在经典的光杠杆法实验方案改进中，也有不少实践研究。比如，改进实验仪器占用空间、简化调试方案以实现快速调节、增加激光指示以方便调节、防止光杠杆和砝码脱落而保障实验安全、拉力传感器代替砝码以实现连续调节和低成本等[6-11]。

即便如此，现有实验装置及实验方案仍然存在较多不足。课题组以垂直光路拉伸法实验方案为平台，将角度传感技术引入到实验中，研制了新型的杨氏模量实验仪、编制实验方案并搭建样机，取得了较好的实验效果。

1 垂直光路拉伸法测量原理

拉伸法测金属丝杨氏模量E的基本公式是：

(1)

其中，L表示金属丝的长度，d表示金属丝的直径，L与d均可测量得到。沿长度方向对金属丝施加一拉力F后，金属丝长度变化ΔL。F为砝码重力或者拉力计所施加，可读取。因金属丝长度变化量极小，传统测量方法失效，故金属丝长度变化量的测量是本实验的关键。下面以垂直光路法说明实验原理，如图1所示。

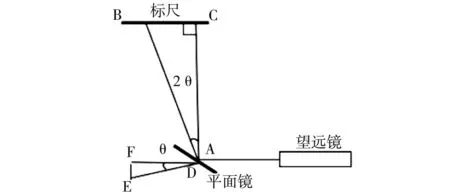
图1 光杠杆法测杨氏模量光路图

当金属丝不悬挂重物(或为了保证金属丝处于竖直而悬挂一基准重物)时，此时光杠杆是水平的，反射镜垂直于光杠杆的上表面，标尺的零刻度点经反射镜反射后能够被观测到。

当金属丝底部悬挂重物时，金属丝被拉长，带动光杠杆的后足向下移动，移动量等于金属丝被拉长的量，大小即图1中EF，光杠杆上表面沿前足逆时针旋转角度θ，即ΔDEF中的∠EDF。后足下移带动反射镜逆时针旋转，旋转角度为2θ，即ΔABC中的∠BAC。根据三角函数的定义，且金属丝变化量极小，则：

(2)

(3)

由式(2)、(3)可以得到：

(4)

式(4)中，EF为待求的金属丝的微小变化量，DE为光杠杆前足和后足之间的距离，可测量得到，AC为实验中标尺到反射镜之间的距离，可测量得到。故通过表达式(4)可得到金属丝的微小变化量。

2 实验存在的问题

根据上述实验原理，式(2)和(3)是在构建了两个直角三角形的基础上根据三角函数定义得到的，所以在开展实验时，首先要在金属丝施加外力(或为了保证金属丝处于竖直状态而悬挂基准重物)时调教光路，构建直角三角形。具体到实验中，则应该是调节望远镜水平、调节平面镜镜片与标尺夹角为45 °。

图2 具体实验时的光路图

经调研：1)实验装置只提供了可以调节反射镜角度以及望远镜倾斜角度的机械结构，没有可供观测的指示信息，也就无法判断是否调节到位，而且受限于实验仪器体积和重量，标尺无法严格调整水平，给实验操作带来了不确定性和差异性；2)实验教材中都提供了类似“调节望远镜的俯仰和高低使其水平”、“调节平面镜的俯仰角”等内容，但未说明具体的判断方法，学生不能准确操作。因此，学生在具体开展实验时，很可能会产生图2所示光路中的AC无法和标尺BC垂直的现象，不能构建理论推导中的直角三角形，据此测量和计算得到的金属丝的微小变化量也就不正确。

3 实验仪器研制

基于上述两个问题，课题组引入角度传感技术，研制一款新型的杨氏模量实验仪。

3.1 设计思路

引入角度检测装置，实现光杠杆平面镜倾角实时测量、显示以及调节，实现标尺倾角的实时测量和显示。引入水平仪，实现望远镜镜筒水平调节。

首先检测标尺的倾角α，然后调节光杠杆平面镜的倾角β，使

β=45°+α/2

(5)

使光路AC与标尺垂直。再使用水平气泡仪监控并调节望远镜底座调节螺丝，使望远镜镜筒水平。如此，就可以实现光路的严格调节。

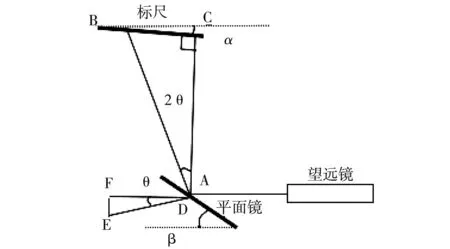
图3 新实验光路图

3.2 实施方案

根据上述分析，新实验装置的核心是倾角检测功能的实现。倾角检测模块分为五部分：电源、倾角检测、调理电路、基于STM32单片机的A/D转换和LCD显示、数据处理及滤波算法如图4所示。

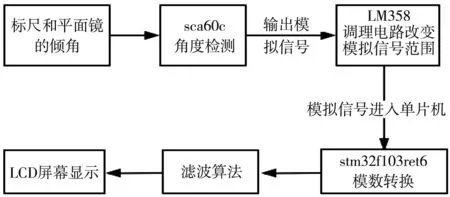
图4 倾角检测系统流程

3.2.1 倾角检测

经调研对比各种角度检测技术，综合考虑检测精度、技术成熟度以及成本等各项因素，最终选定基于3D-MEMS技术的Sca60c型传感器搭建角度检测电路。该传感器的测量范围在±90°，工作电压为直流5 V，输出为输出0.5～4.5 V模拟电压信号，其引脚定义如图5所示。

图5 Sca60c传感器引脚图

传感器的正面有箭头标志，箭头铅直向上则为+1 g，VO端输出4.5 V电压信号，水平放置是为0 g，VO输出2.5 V电压信号，箭头铅直向下为-1 g,VO端输出0.5 V电压信号。

倾角检测电路的输出信号送至调理电路进行放大和滤波处理。

3.2.2 调理电路

因角度传感器的输出信号需要送入单片机进行电压到角度的转换，两者电压范围不匹配，故增加调理电路做预电压匹配处理。STM32单片机模数转化电压范围是0～3.3 V，Sca60c传感器输出信号为0.5～4.5 V，根据需求选用LM358做为调理电路的主芯片，以加法器原理将传感器输出电压信号转化为1～3 V。其电路设计如图6所示。

图6 调理电路原理图

3.2.3 基于STM32单片机的A/D转换和LCD显示

单片机中算法运算使用数字信号，而经过调理电路的电压信号为模拟量，设计中使用STM32F103RET6芯片内置的ADC模数转换器来实现经过调理电路的模拟电压信号转换为数字信号。将模拟电压信号通过ADC模数转换后变为数字信号还需要进行一系列数据处理、公式运算才能得出需要的角度值进行显示。将二进制数值转换为十进制数值带入函数去运算。12位的模数转换器的频率为212，其转换范围为0～3.3 V，显示电压单位为V，需要将A/D转换的数字电压结果乘以330/4096，设其数值定义为变量temp，则有：

(5)

A/D转换精度约为0.8 mV，符合精度要求。

各部分的核心代码如下：

1)A/D转换部分

{

adcx=Get_Adc_Average(ADC_Channel_1,30)；

LCD_ShowString(5,10,200,24,24,"ADC_CH1_VAL：")；

LCD_ShowxNum(149,10,adcx,4,24,0)；

//显示ADC采样值

temp=(float)adcx*(3.3/4096)；

计算出电压值

}

2)LCD显示部分

{

LCD_ShowString(5,45,200,24,24,"ADC_CH1_VOL：0.000V")；

adcx=temp；

b=temp；

LCD_ShowxNum(149,45,adcx,1,24,0)；

//显示电压整数位

temp-=adcx；

temp*=1000；

LCD_ShowxNum(173,45,temp,3,24,0X80)；

//显示电压小数位

b=b-2；

if(b<0)

{

b=-b；

LCD_ShowString(5,80,200,24,24,"angle1 -0..")；

}

else

{

LCD_ShowString(5,80,200,24,24,"angle1 0..")；

}

//区分角度正负号

a=asin(b)*180/3.14159；

//将电压信号转化为角度

c=a；

LCD_ShowxNum(149,80,c,2,24,0)；

//显示角度整数位

a-=c；

a*=10；

LCD_ShowxNum(185,80,a,1,24,0X80)；

//显示角度小数位

LED0=!LED0；

delay_ms(100)；

}

3.2.4 滤波算法

引入滤波算法去除噪波，输出稳定、准确的角度值。由于噪波满足正态分布，可以采用卡尔曼滤波算法，除去噪波。

卡尔曼滤波代码为：

p=p+q；

k=p/(p+r)；

b=vb+k*(b-vb)；

p1=p1-k*p1；

vb1=b；

其中q、r为超参数，需要不断测试，以得到合适的值。

使用上一次的最优结果来预测当前值，同时使用观测值修正当前值，得到最优结果。类似于一阶滞后滤波算法，但是预测值和观测值的加权系数随数据不断变化，使输出值更加平稳。

3.2.5 电源模块

使用电压转换芯片ncv1117dt33t50g、ncv1117st50t3g和，ncv1117dt33t50g将12 V输入电压转换为5 V为传感器供电，ncv1117st50t3g将12 V转化为3.3 V为单片机供电，ams1117-1.5将5 V转化为1.5 V作为调理电路的参考电压，LCD屏幕5 V和3.3 V供电都需要。

3.2.6 样机搭建

上述设计完成后，设计、加工、组装、调试电路板，编写软件程序，完成倾角检测模块的研制，并安装到光杠杆反射镜和标尺的表面，如图7所示。杨氏模量实验系统其他部分与传统实验仪器类似，不做赘述。

图7 倾角检测模块安装图

4 实验方案设计

实验样机搭建完成后，设计了有针对性的实验方案，明确光路调试标准，规范实验操作步骤。实验光路如图8所示。

图8 实验光路图

步骤1：倾角检测系统通电，将光杠杆放置在水平桌面上，旋转平面镜，略微倾斜固定标尺的整个支架，检查倾角检测系统是否能够正常工作。检查螺丝夹能否上下自由移动。

步骤2：将光杠杆的两前足尖放在平台的凹槽内，后足尖放在螺丝夹上端且靠近钢丝处。为保证“工”形光路基准，根据LCD屏显示的标尺倾角α来调整平面镜的倾斜角β，使平面镜与标尺之间成45°夹角，LCD屏显示平面镜倾角为：

(6)

步骤3：将望远镜靠近光杠杆，调节望远镜与光杠杆等高；将望远镜放置于平面镜前约10 cm处，望远镜轴线尽可能接近平面镜水平中线，将水平气泡仪放置在望远镜上，调节望远镜底座的螺母，使其光路水平。此时在望远镜中即可看到标尺虚像。

步骤4：旋转望远镜的目镜直至看到清晰的上下两条水平对称分划线及十字叉丝像，调节望远镜调焦手轮，使望远镜中能看到清楚的平面镜中标尺的像，记下标尺的初始读数x0。

步骤5：每次变动砝码均为1 kg,逐次增加砝码,分别记录标尺读数x1,x2,…,x5的数据和减砝码得到x5,…,x2，x1的数据。

步骤6：用螺旋测微计在钢丝的不同位置测量直径6次，并将数据填入数据记录表中。将光杠杆在实验报告本上压出三个足尖痕，作后足尖f1至前两足尖f2、f3连线的垂线，用游标卡尺测量垂线长度b。

步骤7：测量钢丝长度L以及光杠杆平面镜到标尺的竖直距离D。

5 效果评价

为了客观评价新实验装置的效果，使用实验室现有实验仪作为参照，对同一金属丝测量其杨氏模量值，对比测量结果。实验选用金属丝的长度为750 mm，经多次测量得到其直径为0.597 mm，其杨氏模量真值为190 Gpa。

分别用两种实验装置对同一金属丝开展十次实验，计算其平均杨氏模量值以及平均相对误差，如表1所示。

表1 平均杨氏模量及相对误差数据对比表

为了验证其一致性，将十次实验数据绘制散点图，如图9所示。

图9 十次实验相对误差对比散点图

从表1和图9可以看出，新实验装置所测得杨氏模量值的相对误差在5%以内，而现有装置则在15%～30%。数据表明新实验装置的测量精度有大幅度改善。

6 总 结

以垂直光路为典型案例对拉伸法测量金属丝杨氏模量实验的原理及存在的问题进行了说明。以倾角检测技术为核心研制了一款新型杨氏模量实验仪，并设计了新的实验方案，保证光路调试有规范的方法和明确的标准。组装样机并开展实验，数据表明新的实验装置能够将金属丝杨氏模量测量误差控制在5%以内，较现有装置(约18%～32%)有明显改进；同时，在培养学生严谨治学态度方面也有积极的效果。